4.3. Az MLP konstrukciójának általános kérdései
Az MLP gyakorlati alkalmazásnál − azon túl, hogy meg kell találnunk az adott feladat olyan megfogalmazását, amely alkalmassá teszi, hogy a megoldást neurális hálózat segítségével keressük − számos kérdés merül fel. Ezek a kérdések a konkrét hálózatok konstruálásával, ill. tanításával, stb. kapcsolatosak. Az itt tárgyalni kívánt kérdések valójában mind a gyakorlati alkalmazások kapcsán merülnek föl, a válaszok azonban sokszor komoly elméleti vizsgálat eredményeként születnek. Ugyanakkor az elmélet számos a gyakorlati alkalmazással összefüggő kérdésre még nem ad közvetlenül felhasználható választ. Minthogy a kérdésekre mindenképpen választ kell adjunk, ilyenkor a praktikus megközelítés marad.
A megválaszolandó legfontosabb kérdések a következők:
-
mekkora (hány réteg, rétegenként hány processzáló elem) hálózatot válasszunk,
-
hogyan válasszuk meg a tanulási tényező, μ értékét,
-
milyen kezdeti súlyértékeket állítsunk be,
-
hogyan válasszuk meg a tanító és a tesztelő minta készletet,
-
hogyan használjuk fel a tanító pontokat, milyen gyakorisággal módosítsuk a hálózat súlyait,
-
meddig tanítsuk a hálózatot, stb?
Ezekre és hasonló kérdésekre, melyeket konkrét alkalmazásoknál meg kell válaszolni, minden szempontból kielégítő általános válaszok jelenleg még nincsenek. Nincsenek, vagy csak részben vannak olyan bizonyított eredmények, amelyek adott alkalmazáshoz megadnák, hogy hogyan kell megválasztani a szükséges hálózat méretét. De általában az előbb feltett többi kérdésre is csak tapasztalati válaszok adhatók. Ez az oka annak, hogy az MLP sikeres alkalmazásához jelenleg meglehetősen sok tapasztalat szükséges, amit csak úgy szerezhetünk meg, ha számos, jellegében eltérő feladat megoldására vállalkozunk.
A következőkben az MLP és a back-propagation tanítási eljárással kapcsolatos, az előbbiekben felsorolt néhány gyakorlati szempontot veszünk sorra. A neurális hálózatok alkalmazásánál felmerülő általános kérdésekkel részletesebben a 13. fejezetben foglalkozunk.
A hálózat méretének megválasztása a rétegek számának és az egyes rétegeken belül a neuronok számának meghatározását jelenti. Az elméleti eredmények szerint adott feladat megoldásához − amennyiben az nemlineáris függvényapproximációt igényel − legalább háromrétegű − tehát két tanítható aktív réteggel rendelkező − hálózatra van szükség. A rétegek számának növelése − három, esetleg még több tanítható réteg alkalmazása − azonban megkönnyítheti a feladat megoldását, illetve rétegenként kevesebb processzáló elem felhasználása is elegendőnek bizonyulhat.
A háló méretének meghatározására − a rejtett neuronok számának becslésére − évek óta komoly erőfeszítések történnek. A nem kevés matematikai eredmény, pl. [Kůr92], [Mha94], [Mai99], [Sca98] felső becslést tud adni a rejtett neuronok számára. A kapott eredmények azonban túl pesszimisták. [Kůr92] például a két rejtett réteggel dolgozó MLP-k komplexitására ad meg korlátokat. E szerint adott hibájú approximációhoz az első rejtett rétegben , a másodikban pedig a neuronok elégséges száma, ha a bemenet dimenziója, és . Ez az eredmény egyrészt jól illusztrálja az ún. „dimenzió átka” (curse of dimensionality) problémát, ami röviden azt jelenti, hogy a dimenzió növelésével a komplexitás exponenciálisan nő, másrészt azt mutatja, hogy pl. egy 10-dimenziós problémát már nem tudnánk megoldani a szükséges óriási neuron-szám miatt, ami a gyakorlatnak teljes mértékben ellentmond. Vera Kůrková eredménye ugyanakkor konstruktív, szemben Vitalij Maiorov és Allan Pinkus [Mai99] eredményével, amely bár jóval kisebb háló szükségességét mondja ki, de a konstrukció módjáról nem mond semmit.
E felső becslések tehát a praktikusan szükséges neuronszámnál jóval nagyobb értékeket adnak, így az eredményeknek elsősorban elméleti jelentőségük van, a gyakorlatban még nem alkalmazhatók. Ezeknek a pesszimista elméleti eredményeknek – legalábbis részben – az az oka, hogy az eredmények túl általánosak, mivel olyan korlátokat adnak meg, melyek bármilyen feladatra érvényesek, köztük elfajult, a gyakorlatban igen ritkán előforduló feladatokra is. Konkrét esetekben a neuronhálók konstrukciójánál ezért a processzáló elemek számának meghatározására jelenleg csak a tapasztalatokra támaszkodhatunk.
A gyakorlatban a hálózat méretének meghatározásánál kétféle úton járhatunk. Egyrészt kiindulhatunk egy nagyobb hálózatból, amiről bizonyos tapasztalat birtokában nagy valószínűséggel állíthatjuk, hogy a feladat megoldásához elegendő lesz, majd megkísérelhetjük a hálózatban megmutatkozó redundancia minimális értékre szorítását. Másrészt kisebb méretű hálózatból kiindulva is megpróbálhatjuk a feladatot megoldani, és amennyiben ez nem sikerül, fokozatosan bővíthetjük a hálózatot újabb processzáló elemekkel, ill. rétegekkel.
A redundancia csökkentése azt jelenti, hogy megpróbáljuk megkeresni a felesleges súlyokat, processzáló elemeket, esetleg rétegeket, majd ezeket a hálózatból kimetszve a maradék, egyszerűsített hálózattal oldjuk meg a feladatot. Felesleges súlyoknak, processzáló elemeknek, esetleg rétegeknek azok a hálózatelemek tekinthetők, melyek kihagyásával a feladat megoldható, tehát amelyek vagy nem vesznek részt a kimenet előállításában (pl. egy súly értéke vagy egy processzáló elem kimenete a tanítás során végig nulla, esetleg konstans) vagy amelyek szerepét más hálózatelem is betöltheti, így a hálózat képességeinek redukciója nélkül elhagyhatók.
Ilyen esetre példa, ha két súlyérték vagy processzáló elem kimenete együtt változik a tanítás során, vagy az egyik kimenet a másik konstans-szorosa. Ezekre az eshetőségekre mutat példát a 4.3. ábra, amely a tanító minták függvényében ábrázolja az egyes processzáló elemek kimenő jelének alakulását egy nemlineáris leképzést megvalósító négyrétegű (két rejtett rétegű) hálózatnál.
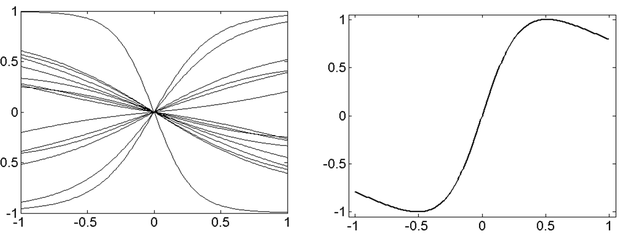
A 4.3. (a) ábra a bemeneti réteg "processzáló elemei"-nek kimenetét mutatja. Minthogy ez a réteg csak erősítési, jelszétosztási feladatot tölt be, nyilvánvaló, hogy a bemeneti "processzáló elemek" egységnyi átvitelt valósítanak meg. A 4.3. (b), (c) és (d) ábrák rendre a második, harmadik és negyedik, egyben kimeneti réteg processzáló elemeinek kimenetét adják meg. Jól látható, hogy mind a második, mind a harmadik rétegben vannak olyan processzáló elemek, melyek a teljes működési tartományban csaknem nulla kimenetet produkálnak, illetve olyan processzáló elem-párok, amelyek kimenete a teljes tartományban együtt mozog, így ezen processzáló elemek, illetve az együttmozgó processzáló elemek egyikének jelenléte felesleges, a hálózatból kimetszhetők.
A hálózatok méretének bizonyos összeköttetések kimetszésével (pruning) történő csökkentésére egyéb módszerek is alkalmazhatók. Ezek a módszerek adott súlyok kimeneti hibára gyakorolt hatása alapján végzik a kimetszéseket. Ha egy súly értékét nullára változatjuk − ezáltal hatását kiiktatjuk − , akkor a kimeneti hiba változása alapján eldönthető, hogy az adott súly lényeges-e a hálózat helyes működése szempontjából vagy nem. Ha a hibanövekedés túl nagy, a kérdéses súlyra (a megfelelő összeköttetésre) szükség van, ellenkező esetben az összeköttetés megszüntethető, kimetszhető.
E módszerek két csoportba sorolhatók:
az egyik csoportba tartozó eljárások a kimeneti hiba egyes súlyok szerinti érzékenységének becslésén alapulnak: a hálózatból a legkisebb érzékenységű súlyok metszhetők ki,
a másik csoportba tartozó módszereknél a kritériumfüggvényhez egy újabb ún. büntető tagot adunk, ezáltal egyfajta regularizációt alkalmazunk.
Az érzékenység-becslés alapján dolgozó eljárások a hibafelület súlyok szerinti Taylor-soros közelítéséből indulnak ki. Másodfokú közelítést alkalmazva szükségük van a hibafelület másodrendű deriváltjait tartalmazó Hesse-féle H mátrixra. Az OBD (Optimal Brain Damage) [LeC90] feltételezi, hogy a Hesse mátrix diagonális, amely általában nem realisztikus feltételezés, az OBS (Optimal Brain Surgeon) [Has92] e feltételezés nélkül dolgozik, így a hibafelületről pontosabb információt használ fel és egyrészt nagyobb mértékű méret-csökkentést eredményez, másrészt ezt valóban a legkevésbé fontos súlyok elhagyásával teszi.
A büntető tagot alkalmazó módszereknél a tanulás során a hálózat súlyainak csökkentésére törekszünk. Ennek megfelelően a büntető tag lehet pl. a hálózat súlyainak négyzetes összege vagy a súlyok abszolút értékének az összege, ami azt jelenti, hogy a kritériumfüggvény minimalizálása során a megfelelő leképezés megtanulásán túl a minél kisebb súlyok elérése a cél. A megtanított hálózatnál a nullához közeli súlyok elhagyásával a hálózat mérete csökkenthető. A módosított kritériumfüggvény lehet pl. a következő [Ish96]:
(4.16)
ahol a hálózat átlagos négyzetes hibája az összes kimenetre és az összes tanító pontra végezve az átlagolást, a második tag a büntető tag, amely a minél kisebb értékű súlyok elérését segíti elő, λ pedig a büntető tag relatív súlyát meghatározó együttható. A súlymódosítás a deriválás elvégzése után:
(4.17)
vagyis a súly abszolút értéke minden tanító lépésben konstans értékkel csökken. Az ilyen tanulási eljárást felejtő tanulásnak (weight decay) is nevezik, hiszen minden egyes tanító lépésben egy súlyfelejtő tagot is alkalmazunk. A felejtő tanulás hátránya, hogy a felejtő tag minden súlynál megjelenik, azoknál is, melyek fontosak a hálózat megfelelő működéséhez, így várhatóan nagyobb hibát eredményez, mint a “sima” back-propagation eljárás. E hatás mérsékelhető, ha a felejtés csak azon súlyokra vonatkozik, melyek abszolút értéke egy adott küszöböt (Θ) nem halad meg. A módosított felejtő tanulásnak megfelelő kritériumfüggvény:
(4.18)
A konstans mértékű felejtéssel szemben szokás exponenciális jellegű felejtést is alkalmazni. Ez utóbbi a súlyok négyzetösszegével arányos büntető tag mellett nyerhető [Pla86]:
(4.19)
A (4.16) és (4.18) összefüggések konkrét példái a regularizációs összefüggéseknek (ld. 2.1. alfejezet), ahol a regularizációs eljárással a négyzetes hiba csökkentése mellett egy járulékos feltétel teljesítése, a súlyok összegének minimalizálása is elérendő cél.
A redundancia csökkentése annak ellenére hasznos lehet, hogy nagyobb méretű hálózat alkalmazása − a nagyobb szabadságfok következtében − sok esetben segíthet a tanítás gyorsításában. A hálózatban meglévő redundanciák azonban általában a szükséges számítások mennyiségét növelik, így nemcsak a hálózat tanításának, hanem a tanított hálózat működésének is csökkentik a sebességét.
A súlyok nagyságának (a súlyvektorok hosszának) leszorítását célzó regularizációs tag alkalmazása nem csupán arra szolgál, hogy elősegítse a hálózat egyszerűsítését, hanem a kisebb súlyok önmagukban is hozzájárulhatnak a háló általánosító-képességének javításához. A regularizáció ilyen szerepéről a bázisfüggvényes hálózatok (6. fejezet) és a kernel gépek (7. fejezet) bemutatásánál részletesen is lesz szó.
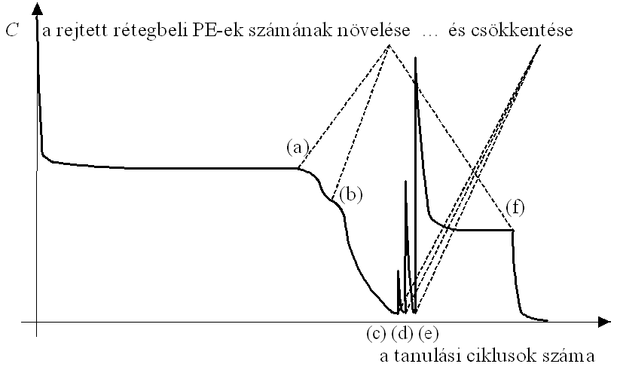
A hálózat bővítésére akkor lehet szükség, ha adott méretű hálózatnál a tanítás hatására már nem csökken a hiba. Újabb processzáló elem beiktatásával a hálózat ismét taníthatóvá válhat, vagyis a kimeneti hibát tovább csökkenthetjük. A folyamat az 4.4 ábrán követhető. Látható, hogy a processzáló elemek számának növelése (az ábrán az (a) és (b) pontok) a hálózat tovább-taníthatóságát, vagyis a hiba további csökkenését eredményezheti. A már kis hibájú hálózatnál ezután kísérletet tehetünk a hálózat egyszerűsítésére. A processzáló elemek számának csökkentése (az ábrán a (c), (d) és (e) pontok) nyilvánvalóan a hiba hirtelen megnövekedését eredményezi, ami azonban tovább-tanítással ismét gyorsan lecsökkenthető, ha az egyszerűbb hálózat is képes a feladat megoldására ((c) és (d)). Ha azonban az így kapott egyszerűbb hálózat már nem alkalmas a feladat megfelelő megoldására (e), a hiba adott határ alá nem szorítható, a hálózat nem tanítható tovább. Jobb eredmény tehát ismét csak akkor nyerhető, ha újra növeljük a hálózat méretét (f ).
Megjegyezzük, hogy az alulról felfelé építkező eljárás, az egyszerűbbtől a bonyolultabb irányában történő hálózat módosítás és az ellenkező irányú, bonyolulttól az egyszerűbb felé történő módosítás általában eltérő hálózat-felépítést és hálózat-méretet eredményez.
A megfelelő méretű hálózat megkeresésének más módszerei is vannak. Alkalmazhatjuk pl. a genetikus algoritmusokat is a feladat szempontjából optimális hálózat-struktúra meghatározására. Ebben az esetben a genetikus algoritmus populációi különböző méretű hálózatokból épülnek fel, és az egyes generációk a feladat szempontjából egyre jobb képességekkel rendelkező hálózatokat fognak tartalmazni. Bármelyik megoldást is választjuk több, különböző méretű hálózat tanítását kell elvégezni, ami a megfelelő méretű hálózat megtalálását és a feladat megoldását meglehetősen lassúvá teszi.
Már az elemi neuronnál láttuk, hogy a tanulási tényező − amit szokás bátorsági tényezőnek is hívni, hiszen az a szerepe, hogy megmondja milyen bátran mehetünk a negatív gradiens irányában − megválasztása alapvetően befolyásolja a tanító eljárás alakulását. Sőt, azt is láttuk, hogy nem megfelelően megválasztott tanulási tényező mellett az eljárás divergens lesz: a hiba nem csökkenni, hanem nőni fog. A bátorsági tényező megfelelő megválasztása tehát az MLP-nél is fontos. Ugyancsak fontos kérdés, hogy adott háló tanításánál milyen kezdeti súlyértékekből induljunk ki, hiszen ez is döntően befolyásolja a tanulás alakulását.
A μ tanulási tényező megválasztására jelenleg nincs egyértelműen javasolható egyszerű módszer. Mint a 2. fejezetben láttuk, egy lineáris processzáló elem esetén meghatározható μ azon értéktartománya, amelyen belül a konvergencia biztosított, sőt az optimális konvergencia-sebességet biztosító μ is megadható. Az optimális konvergencia-sebességet, vagy legalább a konvergenciát biztosító μ meghatározása többrétegű hálózatnál jóval nehezebb, hiszen itt nem biztosítható a kvadratikus hibafelület, így optimális μ-ről nem is beszélhetünk, sokkal inkább olyan μ megválasztási stratégiáról, ahol nem egy rögzített értékű tanulási tényezőt alkalmazunk, hanem a μ értékét lépésről-lépésre változtatjuk. Az is elképzelhető, hogy processzáló elemenként, vagy legalább rétegenként eltérő μ megválasztása indokolt. A legtöbb esetben μ értékét tapasztalati úton határozzák meg általános tendenciák felhasználásával. Kis μ egy minimumhely pontosabb megtalálását, de lassú konvergenciát eredményez, míg nagy μ mellett a konvergencia kezdetben gyorsabb lehet, de a minimumhely megközelítése nehezebb, sőt bizonyos értéknél nagyobb μ mellett a tanítási eljárás konvergenciája sem biztosított, a tanulás alatt a hálózat "elszállhat".
A gyorsabb kezdeti konvergencia és a minimumhely megfelelő pontosságú megközelítése érhető el változó, lépésfüggő μ alkalmazásával. Ebben az esetben valamely kezdeti, viszonylag nagy értékből kiindulva valahány lépésenként csökkentjük μ-t. A csökkentés menetét − mint azt a sztochasztikus szélsőérték-kereső eljárásoknál (2.5.2. rész) említettük − leginkább a sztochasztikus approximáció konvergenciáját biztosító együtthatósorozat csökkentésének menete szerint szokás megválasztani. E szerint a következő követelményeket teljesítő μ(k) sorozat alkalmazható:
. (4.20)
Ebben az összefüggésben k nem feltétlenül a lépésindexet jelöli, μ csökkentésére rendszerint csak néhány lépésenként kerül sor. Láttuk, hogy a fenti feltételeknek eleget tesz pl. a sorozat. A kezdeti érték ( ) megválasztására tapasztalati összefüggés, hogy minél nagyobb a hálózat és minél több az egyes neuronok bemeneteinek száma, annál kisebbre kell választani.
A tanulás konvergenciájának sebessége növelhető adaptív μ választással is. A szokásos eljárás: μ változtatását attól tesszük függővé, hogy a súlymódosítások csökkentik-e a kritériumfüggvény (kockázat) értékét. Ha a hiba nem csökken, akkor μ értéke túl nagy, csökkenteni kell. Ezzel szemben, ha több egymást követő tanító lépés során a hiba folyamatosan csökken, akkor lehetséges, hogy túl óvatosan választottuk meg μ-t, valószínűleg nagyobb érték mellett is biztosított a hiba csökkenése, érdemes tehát nagyobb μ-vel megkísérelni a tanítást. Az irodalomban különböző módosítási stratégiákat találunk, amelyeknél μ növelésének vagy csökkentésének mértéke, illetve a módosítás feltétele különböző. Kis kezdő μ esetén, ha a tanító lépések során a hiba csökken, növeljük a tanulási tényezőt exponenciálisan, míg ha a hiba jelentősen nő, csökkentsük ugrásszerűen [Vog88]. A növelés feltételeként szabható, hogy a hibafelületen egy (lokális) minimumhelyhez képest éppen hol tartunk. Ha a hiba a módosítások során csökken, miközben a gradiens előjele nem változik, növeljük μ értékét. Ezzel szemben, ha a gradiens előjele az egymást követő súlymódosításoknál gyakran változik, ez azt jelenti, hogy egy minimumhely körül ugrál a pillanatnyi megoldásunk, tehát μ értékét csökkenteni kell [Cha87].
Az adaptív μ alkalmazása egzaktabb alapokon is lehetséges, ha figyelembe vesszük a hibafelület alakját. Láttuk, hogy kvadratikus hibafelületnél μ optimális értéke a felület alakjától függ. Többrétegű perceptron esetében a hibafelületen kiterjedt lapos tartományok, továbbá ugrásszerűen változó, hirtelen meredek szakaszok is lehetnek, így attól függően, hogy a hibafelület mely részén mozgunk más és más μ értékre lenne szükség. Az adott lépésben optimális μ meghatározásához azonban az adott hibafelület-rész alakjáról kell, hogy ismeretekkel rendelkezzünk. Dinamikus tanulási tényező optimalizálásra ad eljárást [Yu95], amelynél a hibafelületnek a tanulási tényező szerinti első és második deriváltjára vonatkozó információ segítségével lehetséges gyorsabb konvergenciát biztosító μ megválasztása. (A tanulási tényező megválasztásának kérdésére a későbbiekben a hibavisszaterjesztéses algoritmus változatai c. részben még visszatérünk.)
A súlyok kezdeti értékeinek beállítására − bár természetesen ez is befolyásolja a tanulás konvergenciájának gyorsaságát − jelenleg szintén nincs matematikailag megfogalmazható összefüggés. A kezdeti súlyvektor a hibafelületen a kezdeti pont helyzetét határozza meg, így minél messzebb van ez a pont a megoldás helyétől, ill. minél bonyolultabb a kezdeti pont és a megoldás között a kritériumfelület, annál lassabban tanul a hálózat. Amennyiben valamilyen a priori ismeret rendelkezésünkre áll a hibafelület alakjáról, elhelyezkedéséről, akkor ezt célszerű figyelembe venni a kezdeti értékek megválasztásánál, hiszen így jelentősen gyorsíthatjuk a tanulást. A priori ismeret hiányában a véletlenszerű súlybeállítás a leginkább megfelelő: az egyes súlyokat egy egyenletes eloszlású valószínűségi változó különböző értékeire választhatjuk. A véletlen kezdeti értékek a szimmetriák elkerülését biztosíthatják, megakadályozva, hogy különböző neuronok hasonló leképezést valósítsanak meg és így nemkívánt redundancia jelenjen meg a hálózatban. A véletlen tartomány nagysága befolyásolhatja a konvergencia sebességét, azonban általában itt is csak tapasztalati összefüggés állítható fel: minél nagyobb a hálózat, annál kisebb véletlen értékek választása célszerű. A háló méretétől nem független, viszonylag kis értékek megóvhatnak attól, hogy az egyes neuronok a tanítás túl korai szakaszában az aktivációs függvény telítéses szakaszára kerüljenek.
A hálósúlyok kezdeti értékének megállapításánál azt is figyelembe kell venni, hogy az egyes neuronok kimenetein telítődő nemlineáris függvényt, szigmoid függvényt alkalmazunk. Mind a szigmoid nemlinearitással dolgozó elemi neuron tanításánál, mind az MLP tanításánál láttuk, hogy a súlymódosítás összefüggésében a nemlinearitás deriváltja, sgm’(.) is szerepel, amely, ha a telítéses szakaszon vagyunk, nagyon kicsi is lehet. Törekedni kell tehát arra, hogy a kezdeti értékek beállításánál minél több neuron az „aktív” tartományában működjön, vagyis a neuronok lineáris kimenetei a szigmoid függvények meredek szakaszára essenek. Mint láttuk, ebben a kis kezdeti súlyok segíthetnek. Derrick Nguyen és Bernard Widrow azonban hatékonyabb módszert javasoltak [Ngu90].
A Nguyen-Widrow eljárás olyan módon próbálja a kezdeti súlyokat beállítani, hogy a rejtett réteg neuronjainak aktív tartományai a bemeneti térben lehetőleg egyenletesen legyenek szétosztva, vagyis az egyes neuronok a bemeneti tér más-más tartományában legyenek aktívak és lehetőleg ne legyen olyan bemeneti tartomány, ahol egyetlen neuron sem aktív. Ennek érdekében egyrészt a súlyok célszerű „hosszára” adnak egy összefüggést, másrészt az egyes neuronok eltolásértékének (w0) megfelelő megválasztásával biztosítják az aktív tartományok kellő szétosztását a bemeneti térben. Az eljárás gyakorlati alkalmazása azt mutatja, hogy a Nguyen-Widrow kezdeti-érték beállítással a konvergencia jelentősen, akár nagyságrendekkel is gyorsítható.
A hálók tanításánál a tanítópontokat általában többször, ismételten felhasználjuk, és a tanítást addig folytatjuk, amíg az eljárás vagy magától le nem áll, vagy megfelelően kis hibát el nem érünk. Bár elvileg a gradiens eljárások egy minimumpont elérésekor önmaguktól leállnak, a pillanatnyi gradiens alapú eljárásoknál semmi sem garantálja, hogy nulla gradiens egyáltalán elő fog fordulni. Így legtöbbször a tanulás leállításáról külön gondoskodni kell. Általában előre nem határozható meg a hálózat hibájának alakulása a tanító lépések függvényében, így azt sem lehet megmondani, hogy megfelelően kis hiba eléréséhez hány tanító lépés szükséges. A hálózat "jóságának" kiértékelése, minősítése amúgy is számos elméleti és gyakorlati problémát vet fel. Nem csupán a tanító lépések, hanem a tanító pontok számának meghatározása is kérdéses. (A tanító pontok számának kérdésére ennek a résznek a végén még röviden kitérünk.)
További lehetőségeket jelent, hogy a súlymódosításokat pontonként, vagy kötegelt (batch) eljárás szerint, csak a teljes tanító készlet (epoch) felhasználása után végezzük. Ezek az eljárások a súlykorrekció gyakoriságában térnek el. Az első esetben minden tanító pont alkalmazásánál meghatározzuk a kimeneti hibát és az ebből számítható korrekciós értékkel lépésenként el is végezzük a súlymódosítást. A batch eljárásnál a teljes tanító készlet összes mintáját egyenként, egymás után ráadva a hálózatra minden esetben kiszámítjuk a hibát, de az egyes tanító pontokhoz tartozó hibával nem végzünk korrekciót, hanem az egyedi korrekciókat összegezzük és az akkumulált módosítást végezzük csak el.
Az első esetben tehát a súlymódosítások száma megegyezik a tanító pontok számának és a tanítási ciklusok számának szorzatával, míg a batch eljárásnál csak ciklusonként korrigálunk, ahol egy ciklus a teljes tanító készlet egyszeri felhasználását jelenti. Természetesen a batch eljárásnál nem feltétlenül kell a teljes tanító készletet felhasználni mielőtt egy súlymódosításra sor kerülne. Így valójában a pontonkénti súlymódosítás és a teljes tanító készletenkénti súlymódosítás között bármely eset alkalmazható, amikor a súlymódosítást a pontonkénti esetnél ritkábban, de az epochonkénti esetnél gyakrabban végezzük el.
A két szélső eset nemcsak a korrekciók számában tér el, hanem jellegében is. A mintánkénti tanítás − a pillanatnyi gradiensen keresztül − mintegy zajt visz a rendszerbe, hiszen a pillanatnyi hibaértékek által meghatározott hibafelületen mozgunk, a batch eljárás ezzel szemben átlagoló jellegű. Megjegyezzük, hogy a mintánkénti tanítás nagyon kis μ-vel a batch eljárással ekvivalens megoldásra vezet, ami nem meglepő, hiszen ilyenkor lépésenként olyan kismértékű módosítást hajtunk végre, hogy az átlagoló jelleg megmarad. A mintánkénti tanításból adódó "zaj" sztochasztikus elemet visz a tanításba, ezáltal segíthet a lokális minimumokba való beragadás elkerülésében. Sok esetben tudatosan alkalmazunk zajt a hálózatban − a súlyokhoz vagy a bemeneti mintákhoz véletlenszerű értékeket adunk − így kíséreljük meg a hálózatot egy lokális minimumból kiugratni (ld. még sztochasztikus szélsőérték kereső eljárások, 2.5.2. rész).
További kérdés, hogy egyáltalán hogyan minősítsünk egy hálózatot. Minősítésre több okból is szükségünk van. Egyrészt ennek alapján dönthetjük el, hogy a háló kellően megtanulta-e a feladatot, leállhatunk-e már a tanulással, másrészt ez biztosítja, hogy tudunk arra vonatkozóan mondani valamit, hogy mennyire sikerült a feladatot egyáltalán megtanítani.
A tanulással foglalkozó 2. fejezetben láttuk, hogy a minősítés elvben a kockázat meghatározásával lenne lehetséges. Mivel azonban ehhez a mintapontok eloszlását ismerni kellene, ez az út nem járható. Azt is láttuk, hogy a valódi kockázat − megfelelő feltételek fennállta esetén − a tapasztalati kockázat alapján is becsülhető (ERM elv). A feltételeket a statisztikus tanuláselmélet keretében fogalmazták meg, amely elmélet a valódi kockázatra felső korlátokat is származtatott.
Az MLP minősítésénél az ERM elv és a felső korlátok nem alkalmazhatók. A felső korlátok alkalmazása a háló által megvalósítható függvényosztály VC-dimenziójának ismeretét és azt kívánja, hogy a VC-dimenzió véges legyen. MLP esetén a VC-dimenzió általában nem határozható meg, ugyanakkor az megmutatható, hogy a VC-dimenzió akár végtelen is lehet. Végtelen VC-dimenzió mellett a felső korlátokat megadó (2.31) és (2.33) összefüggések értelmezhetetlenek. A többrétegű perceptronok „jóságának” meghatározására azonban a felső korlátok még akkor sem lennének alkalmazhatók, ha a VC-dimenzió véges lenne, ugyanis a felső korlátok általában túl pesszimisták, konkrét gyakorlati feladat megoldásánál a hálók minősítésére nem használhatók.
A tanítás leállítása érdekében történő minősítés a következőképpen történhet. Adott tanító készlet mellett szükségünk van egy ún. kiértékelő mintakészletre (validation set) is. A hálózat tanítására csak a tanítókészlet mintáit használjuk, míg az adott számú tanító lépésen átesett hálózat minősítése a kiértékelő készletre adott válaszok alapján lehetséges. A kiértékelő készlet olyan be- és kimeneti mintapárokat tartalmaz, amelyek a megoldandó feladatból származnak, és a hálózat normál működési tartományába esnek, de amelyeket a tanításra nem használtunk fel. Az MLP hálózatok általánosító, interpolációs képessége következtében azonban azt várjuk, hogy a megtanított hálózat ezekre, a még sohasem látott mintákra is jó válaszokat szolgáltasson. Amennyiben csak a tanítópontokra adott válaszok alapján értékelünk, túltaníthatjuk a hálózatot. A kiértékelő készlet szerepe éppen az, hogy a túltanítást megakadályozzuk. A tanító eljárás során, bizonyos számú tanító lépést követően a validációs készletre adott válasz hibája alapján dönthetjük el, hogy a háló már kellő mértékben megtanulta-e a feladatot. A minősítő készlet mintáit tehát szintén a tanítás során, de nem a háló tanítására használjuk fel. Szokás ezért a validációs készletet is a tanító készlet részének tekinteni.
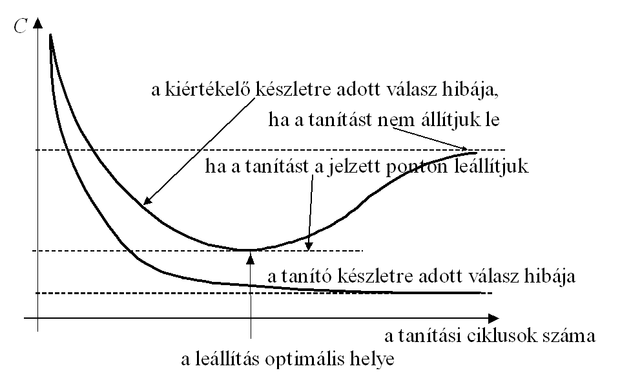
Túltanítás (overtraining) akkor lép fel, ha a tanító készlet mintáira már nagyon kis hibájú válaszokat kapunk, miközben a kiértékelő készletre egyre nagyobb hibával válaszol a hálózat. Ez azért következhet be, mert a hálózat válaszai túlzottan illeszkednek a véges számú tanító pont által megszabott leképezéshez − a tanító pontokban akár tetszőlegesen kis hiba is biztosítható −, miközben a közbenső pontokra adott válaszok jelentősen eltérhetnek a megfelelő kívánt válaszoktól. A túltanulás esetét mutatja a 4.5 ábra tanulási görbéje.
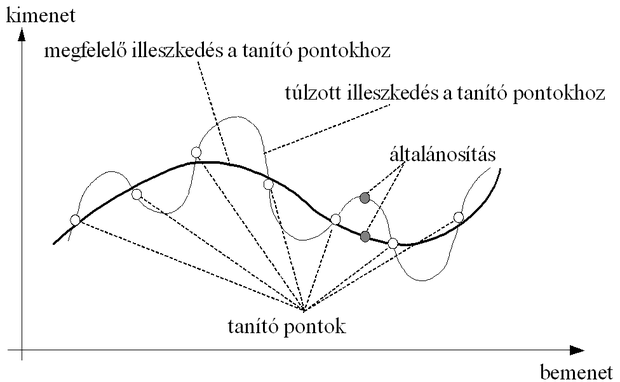
Az ábra alapján látható, hogy a tanítást a megjelölt helyen − vagyis amikor a tanító mintákra adott válasz hibája ugyan még csökken, de a kiértékelő (validációs) mintákra már növekedni kezd – leállítva, a hálózat működése jobban közelít a kívánt leképzéshez. Ezt a leállítási stratégiát korai leállításnak nevezzük. A túltanulás következtében beálló tanítópontokhoz való túlzott illeszkedés (overfitting) hatását a leképezésre a 4.6. ábra illusztrálja.
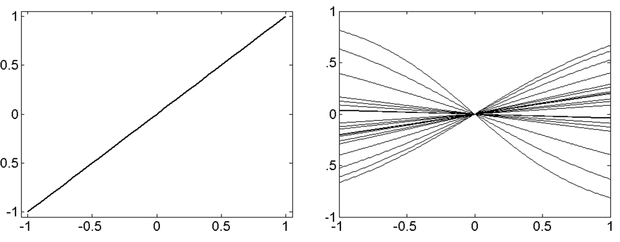
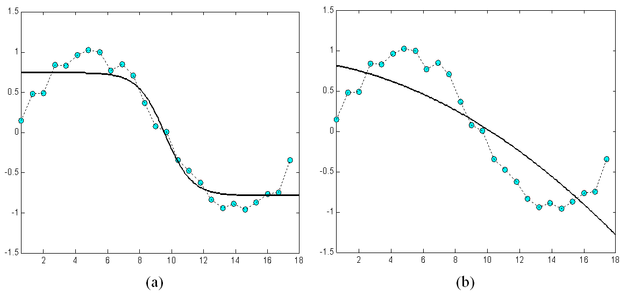
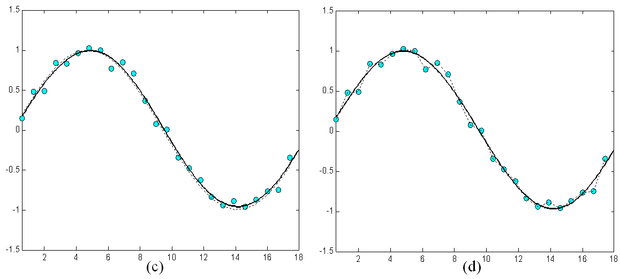
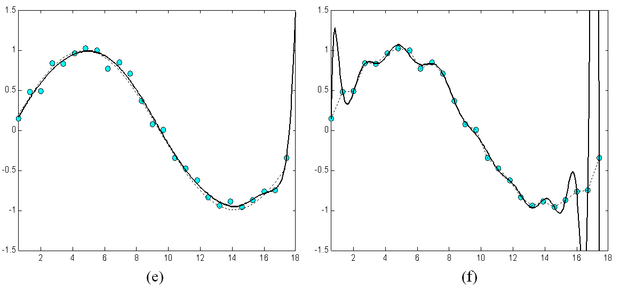
A tanító pontokhoz való túlzott illeszkedés a hálózat általánosító-képességét rontja. Túltanulás elsősorban akkor következhet be, ha a hálózat mérete − a hálózat szabadságfoka − a tanító pontok számához viszonyítva túl nagy. A helyzet hasonló ahhoz az esethez, amikor polinomiális regressziónálkevés mintapontra akarunk nagyfokszámú polinomot illeszteni. A fokszám csökkentésével − esetleg a mintapontokbeli tökéletes illeszkedés rovására − a pontsorozat általános trendjének követése inkább lehetséges. A 4.7 ábra arra ad példát, hogy egy egyszerű függvény approximációjánál a szabad paraméterek számának növelése milyen mértékben növelheti a túltanulás esélyét. Az ábrán a szinusz függvény egy periódusát közelítjük polinomiális approximációt és MLP-t alkalmazva. A 4.7 (c) és (e) ábrák különböző komplexitású MLP-k eredményei: az első egy rejtett neuront, a második ötöt, a harmadik húszat használ. A (b), (d) és (f) ábrák hasonlóan egyre nagyobb komplexitású polinomiális közelítés eredményei, rendre másod- ötöd- és huszadfokú polinommal történt approximációk. Látható, hogy miközben az MLP-nél a szabad paraméterek számának sokszorosára növelése alig rontott az approximáció minőségén, a polinomiális approximációnál ez a hatás igen jelentős. A polinomiális approximáció sokkal érzékenyebb a paraméterek számának megfelelő megválasztására. A túl nagy fokszám jelentős túlilleszkedést eredményezett. Az ábra ugyanakkor azt is mutatja, hogy túl kevés szabad paraméter mellett mindkét eszköz esetében nagy lesz a hiba, ami természetes is, hiszen ilyenkor az approximáló rendszer képessége nem elegendő a feladat megoldására.
Miközben általánosan igaz, hogy a túl sok szabad paraméter túltanulásra és túlilleszkedésre vezet, az MLP hálózatoknál viszonylag tág határok között megválaszthatjuk a háló méretét anélkül, hogy jelentős mértékben túltanulást tapasztalnánk. Ez, a mindenképpen előnyös tulajdonság egyfajta implicit regularizációként értelmezhető, hiszen anélkül, hogy bármilyen simasági mellékfeltételt alkalmaztunk volna, a háló a tanítópontokra illeszthető végtelen sok lehetőség közül a simább válaszokat előnyben részesíti. Ez a tulajdonság a polinomiális approximációra már nem mondható el.
A tanító és a kiértékelő mintakészleteken kívül szokás még egy ún. minősítő (test) készletet is definiálni, amely szintén az adott problémából származó összetartozó be- kimeneti mintapárok halmaza, és amely mintapárokat a tanításnál egyáltalán nem használunk fel. A minősítő készlet a megtanított háló végső értékelésére, a háló általánosító-képességének becslésére használható. A rendelkezésre álló mintapontokat egy problémánál ezért három részre, tanító-, kiértékelő- és tesztelő készletre kell bontanunk. Kellően nagyszámú adat mellet ez nem okoz nehézséget. Ha azonban kevés adat áll rendelkezésünkre (ez számos gyakorlati feladatnál előfordulhat vagy az adatok beszerzésének nagy költsége, vagy az adatoknak a probléma természetéből adódó kis száma miatt), a három diszjunkt készletre bontás azt eredményezheti, hogy az egyes részfeladatok elvégzéséhez túl kevés mintapontunk marad. Így, ha viszonylag sok pontot használunk fel a tanításra, és kevés marad a megtanított hálózat minősítésére, nem lehetünk biztosak a megtanított hálózat képességeit illetően.
Ezzel szemben, ha a minősítésre hagyunk több mintapontot és ezért kevés tanító pontunk lesz, csak azt konstatálhatjuk − bár ezt kellő biztonsággal tehetjük −, hogy a hálónk meglehetősen gyengén tanulta meg a feladatot. Nem közömbös tehát, hogy a mintakészlet mekkora hányadát használjuk tanításra és mekkorát minősítésre.
A megfelelő arányok meghatározására számos elméleti és gyakorlati eredmény született. A mintahalmaznak a korai leállításhoz szükséges két részre bontásával foglalkozik pl. [Guy96] és [Kea96]. Ezek az eredmények a VC-dimenzió alapján meghatározható korlátok felhasználásával adnak javaslatot a mintapontok tanító és kiértékelő halmazokra bontásához. Az ezzel kapcsolatos nehézségeket az előbbiekben említettük, itt azonban a helyzet kedvezőbb, hiszen nem a tényleges kockázatnak a gyakorlati alkalmazás szempontjából is használható becslése a cél, hanem csupán a mintakészlet megfelelő bontása. A különböző megközelítések alapján született eredményeket itt nincs módunk ismertetni, csupán egy megközelítés gyakorlatban jól alkalmazható eredményeit foglaljuk össze röviden.
Amari és munkatársai a tanítópontok két részre történő bontását vizsgálták azzal a céllal, hogy a túltanulás korai leállítással történő elkerüléséhez a megfelelő tanító/kiértékelő arányt meghatározzák [Ama97]. A megfelelő arány függ a háló komplexitásától, a háló szabad paramétereinek számától is. Ha a tanító pontok száma P kisebb vagy közel egyenlő a háló szabad paramétereinek számával (m), akkor nagy a túltanulás veszélye, hiszen ilyenkor a háló elvileg is képes az összes tanítópontot megtanulni, memorizálni. Ha ugyanekkor még kevés pontunk van − ahogy ezt az előbb már említettük − akkor a pontkészlet két készletre történő hasítása nem oldja meg a problémát: túl kevés mintapont marad a háló tanítására. Ekkor a túltanulás elkerülésére a 2. fejezetben említett regularizációs technikát alkalmazhatjuk. Megmutatható ugyanis, hogy a korai leállítás és a megfelelő mellékfeltétellel végzett regularizáció hasonló eredményre vezet [Bis95].
Ha a súlyok számához képest nagyon sok mintapontunk van (P > 30m), akkor megmutatható, hogy korai leállításra nincs szükség, helyesebb, ha a rendelkezésre álló pontokat mind tanításra használjuk. A két szélsőség között (P < 30m, de P > m) játszik fontos szerepet a korai leállítási technika. Ehhez viszont valóban szükséges a mintapontok tanító és értékelő készletre való bontása. Amari eredményei azt mutatják, hogy − feltéve, hogy m elegendően nagy − a legjobb stratégia, ha mindössze pontot használunk kiértékelésre, a többit pedig tanításra. Ha pl. a szabad paraméterek száma m=100, akkor a pontok 7%-át kell kiértékelésre használnunk és a maradék 93%-ot tanításra.
Kevés pont esetén az előbbi indokok miatt a végső minősítés céljait szolgáló teszt készlet sem különíthető el a mintakészletből. Ilyenkor a már említett (ld. 2. fejezet) kereszt kiértékelési (cross validation) eljárást alkalmazhatjuk (pl. [Sto78]).
A háló mérete, a felhasznált tanító pontok száma és a háló hibája a teszt készleten, vagyis a háló általánosító-képessége nem függetlenek egymástól. Az eddigiekben vizsgált kérdések tehát valójában csak egymással összefüggésben tárgyalhatók. Az alábbiakban e kérdéshez kapcsolódó két általános alaperedményt említünk meg, melyek a hálók osztályozó, illetve függvényapproximációs képességeikre vonatkoznak.
Az első általános eredmény, amely Eric Baum és David Haussler nevéhez fűződik [Bau89], osztályozós hálókra vonatkozik. Arra ad választ, hogy mekkora tanító készlet szükséges adott méretű hálózat megtanításához, ha a megtanított háló általánosító-képességéről valamilyen állítást is szeretnénk megfogalmazni.
Legyen egy M processzáló elemből álló, m súllyal rendelkező hálónk. Legyen . Bizonyítható, hogy ha tetszőleges eloszlású mintát tanítunk a hálónak, és a tanító minták legalább -ed részét a megtanított háló helyesen osztályozza, akkor ugyanebből a feladatból származó, de a tanításnál fel nem használt tesztelő minták legalább -od részét is 1 valószínűséggel helyesen fogja osztályozni a háló.
Ha eltekintünk a logaritmikus tényezőtől, akkor a szükséges tanítópontok száma, a súlyok (szabad paraméterek) száma és az osztályozási hibára jellemző konstans ε között az alábbi közelítő kapcsolat áll fenn: , ami megegyezik a Widrow által megfogalmazott ökölszabállyal. Ez azt jelenti, hogy pl. 10 %-os általánosító hiba eléréséhez a tanító pontok számát legalább a háló szabad paraméterei számának tízszeresére kell választani.
Függvényapproximációs feladatokra Barron jutott az előzőhöz hasonló jellegű eredményre [Bar93]. Az eredmény többrétegű perceptronapproximációs tulajdonsága, az approximálandó függvény jellemzői és a háló mérete között ad kapcsolatot. Mint az előzőekben láttuk az MLP hálózatok egyetlen szigmoid nemlinearitású rejtett réteggel és lineáris kimeneti réteggel univerzális approximátorok, amennyiben a rejtett rétegben elegendő neuron található. Egy konkrét háló és approximálandó függvény esetében a háló approximációs képessége, általánosítása azzal az eltéréssel jellemezhető, mely az approximálandó és a háló által megvalósított approximáló függvény között van. Négyzetes értelemben véve az eltérést (négyzetes veszteségfüggvényt alkalmazva) az approximáció kockázatának (ld. 3. fejezet) egy felső korlátja határozható meg. Barron eredménye szerint:
, (4.21)
ahol az approximálandó függvény regularitására, "változékonyságára" jellemző mennyiség, M a háló rejtett rétegbeli neuronjainak száma, N a bemenet dimenziója és P a tanító pontok száma. Az összefüggés mutatja a háló méretének az általánosításra, az approximáció jóságára vonatkozó ellentmondásos hatását. Az előző megfontolásoknál már utaltunk rá, hogy ha a rejtett rétegbeli neuronszám túl kicsi, a háló nem képes a megfelelő változékonyságú függvény kellően kis hibájú közelítésére. Ugyanakkor a tanítópontok számához viszonyított túl nagy háló túlilleszkedésre hajlamos, így az általánosítási hiba ezért lehet nagy. A korlát két tagja ezt a két ellentétes hatást fejezi ki.
A hibavisszaterjesztéses algoritmusnakszámos változatát dolgozták ki. A változatok célja egyrészt a konvergencia gyorsítása (pl. momentum módszer), másrészt a hibafelületen jelentkező lokális minimumokba való beragadás elkerülése. A back-propagation eljárás a hibafelület gradiense alapján számol, tehát a tanítás alapjául lényegében bármely gradiens alapú eljárás szóba jöhet. Így alkalmazzák MLP hálózatok tanítására a konjugált gradiens módszert,a Levenberg-Marquart eljárást, de a rekurzív legkisebb négyzetes hibájú (recursive least square, RLS) [Leu01] és a Kalman szűrő alapú eljárás [Sha92], [Iig92], [Sum99] is szokásos. A különböző módszerek eltérő lépésszám alatt érik el a megfelelő kis hibájú megoldást, azonban az egyes lépésekhez szükséges számítások mennyisége is jelentősen eltérhet, így a kisebb lépésszámú eljárások összességében nem feltétlenül eredményeznek kedvezőbb tanulást.
A gradiens alapú eljárásoktól alapvetően eltérnek a véletlen keresési módszerek (véletlen keresés, genetikus algoritmusok), melyeket szintén alkalmazhatunk a megfelelő súlyok megtalálására. Ezen módszerek előnye, hogy globális keresést végeznek, nem igénylik a gradiens meghatározását, így akkor is alkalmazhatók, ha a hibafüggvény nem differenciálható. Mindezek következtében lokális minimumokba való beragadásuk kevésbé valószínű. A "feltételgyengítések" és a lokális minimumokba való beragadási esély csökkentésének ára – különösen nagyméretű hálózatoknál – a jelentős számítási igény. A véletlen keresés (random search) bizonyítottan megtalálja a globális minimumot (ld. 2. fejezet), ha a bemeneti súlytér kompakt. E feltétel az MLP súlyaira nem biztosítható, ezért nem garantált, hogy a véletlen kereséssel eljutunk a globális minimumhoz.
Genetikus algoritmus esetén a hálózat súlyaiból kell kialakítanunk a kromoszómákat, a jóságfüggvény szerepét pedig pl. a hibafüggvény (-1)-szerese töltheti be. A kromoszómák kialakításának egy lehetséges módja, hogy a súlyértékek bináris reprezentációiból képezünk bitfüzéreket, minden egyes bitfüzér egy adott struktúrájú és adott súlyokkal rendelkező hálónak felel meg. Természetesen más reprezentáció is lehetséges. A genetikus algoritmusok egyik erőssége, hogy nem igényli a gradiens meghatározását hátrány is lehet, amennyiben a gradiens információ rendelkezésünkre áll. Ha tehát a gradiens ismert, célszerű felhasználni, hiszen ez járulékos információ a hibafelületről, így felhasználása a genetikus keresést gyorsíthatja. Az eltérő eljárások kombinálása általában is hasznos lehet. Pl. valamely véletlen keresési eljárással próbálunk először a minimumhely közelébe eljutni, ahonnan már egy gradiens alapú algoritmussal a minimum pontos helye megtalálható.
Az említett tanulási eljárásokkal részletesen a 2. fejezetben foglakoztunk, így itt csak az ún. momentum módszert foglaljuk össze.
A momentum módszer olyan heurisztikus eljárás, ahol az egyes lépésekben a súlymódosítás meghatározása két részből áll. Először a gradiens módszernek megfelelően meghatározunk egy súlymódosító értéket, azonban nem ezzel végezzük el a korrekciót, hanem még figyelembe vesszük az előző módosítás hatását is. A súlymódosítás ennek megfelelően:
(4.22)
ahol η az ún. momentum együttható, amelynek értéke 0 és 1 között kell legyen (gyakori választás a 0,8 körüli érték). Az új tag tehetetlenséget visz az eljárásba, hiszen az adott lépésben a módosítás irányában szerepet kap az előző irány, s így közvetve a régebbi irányok is. A momentum módszerkülönösen kedvező, ha a hibafelületen keskeny völgy húzódik végig, és a momentum tag nélkül a megoldás felé ezen völgy környezetében túl sok iteráció megtételével haladnánk. A momentum módszer (4.22) összefüggéséből látható, hogy ez formailag megegyezik a konjugált gradiens módszerrel (ld. 2.5.1. alfejezet), ahol szintén a pillanatnyi gradiens és az előző irány eredője irányában történik az elmozdulás. Azonban míg a konjugált gradiens módszer olyan szélsőérték-kereső eljárás, amely kvadratikus hibafelület esetén bizonyítottan N lépésben konvergál (N-dimenziós hibafelület esetén) és ahol az egyes tagok együtthatói meghatározhatók (ld. (2.78) és (2.86) összefüggések), addig a momentum módszer heurisztikus eljárás, ahol mind μ, mind η megválasztása tapasztalati úton történik.
Az előzőekben utaltunk már a μ megválasztásánál felmerülő nehézségekre. Mivel mind μ, mind η megválasztása a hibafelület függvénye, felmerül a két tényező együttes optimalizálásának igénye is. E megközelítés alapján javasol paraméter megválasztást [Yu97]. Az eljárás alapgondolata, hogy olyan – optimális – μ és η lépésnagyságokat határozunk meg, melyek biztosítják, hogy a következő tanító lépés során kapott súlyok a lehető legnagyobb mértékben csökkentik a hibát. Ehhez a hibafelület μ és η szerinti első és második deriváltjait kell meghatározni, azonban mivel a deriváltak számításánál az eredeti hibavisszaterjesztéses eljárás részeredményei felhasználhatók, a járulékos számítások mennyisége nem jelentős. A módszer alkalmazásával – a számítási igényeknek a klasszikus back-propagation eljáráshoz viszonyított 2-3-szoros megnövelése árán – nagyságrendi sebességjavulás érhető el. Eredőben tehát adott hibahatár elérése kevesebb számítással, gyorsabban lehetséges.
A többrétegű, hibavisszaterjesztésen alapuló tanítással dolgozó hálózatok számos alkalmazási lehetőséggel rendelkeznek. Gyakori alkalmazásukat kedvező tulajdonságaik, bizonyított approximációs képességük és viszonylag egyszerű felépítésük indokolják. Az alkalmazási területekkel és néhány érdekes alkalmazási példával a 7. fejezetben találkozhatunk.
Feladatok
4.1 Oldja meg a XOR problémát egy rejtett rétegű MLP hálózattal. Törekedjen a lehető legegyszerűbb hálózat elérésére. Rajzolja fel a feladat hibafelületét.
4.2 Mutassa meg, hogy a XOR probléma megoldható egy két neuronból (egy rejtett és egy kimeneti neuron) álló hálózattal. Határozza meg a háló súlyait. Rajzolja fel a háló által megvalósított elválasztó felületet.
4.3 Vizsgálja meg a kezdeti súlyértékek megválasztásának hatását a tanító eljárás konvergencia-sebességére. Válasszon nagyságrendileg eltérő kezdeti súlyértékekeket. A vizsgálatot különböző feladatoknál (egydimenziós bemenet, pl. , kétdimenziós bemenet, pl. XOR, és egy sokdimenziós osztályozási probléma, pl. karakterfelismerés 10x14 pixeles bináris képek alapján) végezze el.
4.4 Konstruáljon egy, az függvényt approximáló MLP-t. Törekedjen a minél egyszerűbb hálózatra. Milyen aktivációs függvényt célszerű választania a kimeneti réteg neuronjánál: logisztikus, tangens hiperbolikus vagy lineáris függvényt?
4.5 Konstruáljon MLP-t, amely megoldja a két egymásba tekeredő spirál szétválasztását. Vizsgálja meg, hogy hogyan befolyásolja a tanítás gyorsaságát és a háló méretét, ha egy, illetve ha két rejtett réteget alkalmaz.
4.6 Oldja meg a paritásproblémát (N-bites bemeneti minták páros és páratlan paritású csoportokra való szétválasztása) MLP hálózattal. Adjon magyarázatot, hogy miért "nehéz" ez az egyszerű feladat egy MLP-nek.
4.7 Vizsgálja meg a momentum módszer hatását a konvergencia-sebességre. Oldja meg a 4.5 feladatot, de most alkalmazzon momentum tagot is a tanításnál. Kísérletileg elemezze, hogy milyen irányban és mértékben befolyásolja a tanulási tényező és a momentum faktor a tanulás sebességét.
4.8 Konstruáljon egy, az függvényt approximáló MLP-t. Vizsgálja meg, hogy a háló méretének nagyfokú változtatása milyen hatással van az eredményre. Próbálkozzon néhány (5-6) és néhányszor tíz (30-50) rejtett neuronnal.
4.9 Alkalmazzon az előző feladatra egy súlyminimalizáló regularizációs tanító eljárást a néhányszor tíz neuronnal felépített esetre. Próbálja a háló méretét ennek segítségével redukálni.