A hibavisszaterjesztéses algoritmusta 4.1 ábrán látható MLP architektúra segítségével fogjuk származtatni. Az algoritmus egy pillanatnyi gradiensen alapuló iteratív tanuló eljárás, melynek származtatásánál az elemi neuron tanításánál alkalmazott utat fogjuk követni. Minthogy iteratív eljárásról van szó, az egyes súlyok, illetve súlyvektorok lépésenkénti módosító összefüggéseit írjuk fel. A már bevezetett jelöléseken túl k szolgál a diszkrét lépésindex jelölésére. Így $w_i^{(l)}\left(k\right)$ az l-edik réteg, i-edik processzáló elemének a k-adik időpillanatban érvényes súlyvektorát, $w_{ij}^{(l)}\left(k\right)$ pedig értelemszerűen ugyanezen súlyvektornak a j-edik komponensét jelöli.

A hálózat tanítását két (aktív) rétegű hálózaton mutatjuk be, de az eredmények természetes módon kiterjeszthetők tetszőleges rétegszámra is.

Először írjuk fel a háló kimeneti négyzetes hibáját a k-adik lépésben.

${\epsilon }^2\text{(}k\text{)}={\epsilon }_1^2\text{(}k\text{)}+{\epsilon }_2^2\text{(}k\text{)}={\left(y_1\text{(}k\text{)}-d_1\text{(}k\text{)}\right)}^2+{\left(y_2\text{(}k\text{)}-d_2\text{(}k\text{)}\right)}^2$ . (4.2)

A súlymódosításhoz a megfelelő súlyok szerinti pillanatnyi deriváltakat

${\nabla }_{ij}^{\text{(}l\text{)}}\text{(}k\text{)}=\frac{\partial {\epsilon }^2\text{(}k\text{)}}{\partial w_{ij}^{\text{(}l\text{)}}\text{(}k\text{)}}$ (4.3)

illetve a súlyvektorok szerinti pillanatnyi gradienseket

${\nabla }_i^{\text{(}l\text{)}}\text{(}k\text{)}=\frac{\partial {\epsilon }^2\text{(}k\text{)}}{\partial w_i^{\text{(}l\text{)}}\text{(}k\text{)}}$ (4.4)

kell kiszámítani. A továbbiakban a (k) lépésindexet csak ott fogjuk jelölni, ahol ez az érthetőség miatt szükséges.

A kimeneti rétegnél (l=L=2) a pillanatnyi derivált (gradiens) megegyezik a szigmoid nemlinearitással rendelkező elemi neuronnál meghatározott deriválttal (gradienssel), hiszen a kimeneti réteg processzáló elemeinek működése semmiben sem tér el az egyetlen, szigmoid kimeneti nemlinearitással rendelkező PE működésétől.

$\frac{\partial {\epsilon }^2}{\partial w_{ij}^{\text{(}2\text{)}}}=-2{\epsilon }_i\text{sg<msup> m <mo>′</mo> </msup>}\left(s_i^{\text{(}2\text{)}}\right)x_j^{\left(2\right)}=-2{\delta }_i^{\left(2\right)}{x}_j^{\left(2\right)}$ , (4.5)

illetve vektoros formában írva:

$\frac{\partial {\epsilon }^2}{\partial w_i^{\text{(}2\text{)}}}=-2{\epsilon }_i\text{sg<msup> m <mo>′</mo> </msup>}\left(s_i^{\left(2\right)}\right)x^{\left(2\right)}=-2{\delta }_i^{\text{(}2\text{)}}{x}^{\text{(}2\text{)}}$ (4.6)

A súlymódosítás tehát

$w_i^{\left(2\right)}\left(k+1\right)=w_i^{\left(2\right)}\left(k\right)+2\mu {\epsilon }_i\left(k\right)\text{sg<msup> m <mo>′</mo> </msup>}\left(s_i^{\left(2\right)}\text{(}k\text{)}\right)x_{}^{\left(2\right)}\left(k\right)=w_i^{\left(2\right)}\left(k\right)+2\mu {\delta }_i^{\left(2\right)}\left(k\right)x_{}^{\left(2\right)}\left(k\right)$ (4.7)

A rejtett réteg processzáló elemeinél a fenti összefüggések közvetlenül nem alkalmazhatók, mivel nem ismerjük az egyes processzáló elemek kimenetén fellépő hibát. A lánc-szabály alkalmazásával azonban a deriváltakat itt is meg tudjuk határozni, hiszen a rejtett réteg processzáló elemeinek súlytényezői befolyásolják ezen processzáló elemek lineáris (s) és nemlineáris (y) kimeneteit, továbbá ezen kimeneteken keresztül a későbbi rétegek kimeneteit is. Tehát a parciális deriváltak lépésenként számíthatók.

$\begin{array}{l}\frac{\partial {\epsilon }^2}{\partial w_{ij}^{\text{(}1\text{)}}}=\frac{\partial {\epsilon }^2}{\partial s_i^{\text{(}1\text{)}}}\frac{\partial s_i^{\text{(}1\text{)}}}{\partial w_{ij}^{\text{(}1\text{)}}}=\frac{\partial \left({\epsilon }_1^2+{\epsilon }_2^2\right)}{\partial s_i^{\text{(}1\text{)}}}\frac{\partial s_i^{\text{(}1\text{)}}}{\partial w_{ij}^{\text{(}1\text{)}}}=\frac{\partial {\epsilon }_1^2}{\partial s_i^{\text{(}1\text{)}}}\frac{\partial s_i^{\text{(}1\text{)}}}{\partial w_{ij}^{\text{(}1\text{)}}}+\frac{\partial {\epsilon }_2^2}{\partial s_i^{\text{(}1\text{)}}}\frac{\partial s_i^{\text{(}1\text{)}}}{\partial w_{ij}^{\text{(}1\text{)}}}\\ =2{\epsilon }_1\frac{\partial {\epsilon }_1^{}}{\partial s_i^{\text{(}1\text{)}}}\frac{\partial s_i^{\text{(}1\text{)}}}{\partial w_{ij}^{\text{(}1\text{)}}}+2{\epsilon }_2\frac{\partial {\epsilon }_1^{}}{\partial s_i^{\text{(}1\text{)}}}\frac{\partial s_i^{\text{(}1\text{)}}}{\partial w_{ij}^{\text{(}1\text{)}}}\end{array}$ (4.8)

Ismét a lánc-szabályt alkalmazva a hibakomponensek parciális deriváltjai meghatározhatók.

${\epsilon }_1$ -re bemutatva:

$\frac{\partial {\epsilon }_1^{}}{\partial s_i^{\text{(}1\text{)}}}=\frac{\partial {\epsilon }_1^{}}{\partial s_1^{\text{(}2\text{)}}}\frac{\partial s_1^{\text{(}2\text{)}}}{\partial y_i^{\text{(}1\text{)}}}\frac{\partial y_i^{\text{(}1\text{)}}}{\partial s_i^{\text{(}1\text{)}}}=-sg{m}^{\prime }\left(s_1^{\left(2\right)}\right)w_{1i}^{\left(2\right)}sg{m}^{\prime }\left(s_i^{\left(1\right)}\right)$ , (4.9)

majd az ${\epsilon }_2$ -re hasonlóan nyerhető deriváltat felhasználva a gradiens a következőre adódik:

$\begin{array}{l}\frac{\partial {\epsilon }^2}{\partial w_{ij}^{\left(1\right)}}=-2{\epsilon }_1\text{sg<msup> m <mo>′</mo> </msup>}\left(s_1^{\text{(}2\text{)}}\right)w_{1i}^{\left(2\right)}\text{sg<msup> m <mo>′</mo> </msup>}\left(s_i^{\text{(}1\text{)}}\right)\frac{\partial s_i^{\text{(}1\text{)}}}{\partial w_{ij}^{\left(1\right)}}-2{\epsilon }_2\text{sg<msup> m <mo>′</mo> </msup>}\left(s_2^{\text{(}2\text{)}}\right)w_{2i}^{(2)}\text{sg<msup> m <mo>′</mo> </msup>}\left(s_i^{\text{(}1\text{)}}\right)\frac{\partial s_i^{\text{(}1\text{)}}}{\partial w_{ij}^{\left(1\right)}}\\ =-\left(2{\delta }_1^{\left(2\right)}{w}_{1i}^{\left(2\right)}+2{\delta }_2^{\left(2\right)}{w}_{2i}^{\left(2\right)}\right)\text{sg<msup> m <mo>′</mo> </msup>}\left(s_i^{\text{(}1\text{)}}\right)x_j^{\left(1\right)}=-2{\delta }_i^{\left(1\right)}{x}_j^{\left(1\right)},\end{array}$ (4.10)

és így a súlymódosítás

$\begin{array}{l}{w}_i^{\left(1\right)}\left(k+1\right)=w_i^{\left(1\right)}\left(k\right)+2\mu \left({\delta }_1^{\left(2\right)}\left(k\right)w_{1i}^{\left(2\right)}\left(k\right)+{\delta }_2^{\left(2\right)}\left(k\right)w_{2i}^{\left(2\right)}\left(k\right)\right)sg{m}^{\prime }\left(s_i^{\left(1\right)}\left(k\right)\right)x_{}^{\left(1\right)}\left(k\right)\\ =w_i^{\left(1\right)}\left(k\right)+2\mu {\delta }_i^{\left(1\right)}\left(k\right)x_{}^{\left(1\right)}\left(k\right),\end{array}$ (4.11)

ahol

${\delta }_i^{\left(1\right)}=\left({\delta }_1^{\left(2\right)}{w}_{1i}^{\left(2\right)}+{\delta }_2^{\left(2\right)}{w}_{2i}^{\left(2\right)}\right)sg{m}^{\prime }\left(s_i^{\left(1\right)}\right)$ (4.12)

az ún. "visszaterjesztett hiba". A súlymódosítás tehát itt is az LMS algoritmussal formailag megegyező eljárással történik, a hiba helyén azonban súlyozott, "visszaterjesztett hiba" szerepel. A súlyozó együtthatók megegyeznek az adott hálózat-részben az előrecsatolásnál szereplő súlytényezőkkel. A súlymódosítás ennek alapján tetszőleges rejtett rétegre megadható:

$\begin{array}{l}{w}_i^{\left(l\right)}\left(k+1\right)=w_i^{\left(l\right)}\left(k\right)+2\mu \left({\displaystyle \sum _{r=1}^{N_{l+1}}{\delta }_r^{\left(l+1\right)}\left(k\right)w_{ri}^{\left(l+1\right)}\left(k\right)}\right)sg{m}^{\prime }\left(s_i^{\left(l\right)}\left(k\right)\right)x_{}^{\left(l\right)}\left(k\right)\\ =w_i^{\left(l\right)}\left(k\right)+2\mu {\delta }_i^{\left(l\right)}\left(k\right)x_{}^{\left(l\right)}\left(k\right)\end{array}$ (4.13)

ahol a "visszaterjesztett hiba":

${\delta }_i^{\left(l\right)}\left(k\right)=\left({\displaystyle \sum _{r=1}^{N_{l+1}}{\delta }_r^{\left(l+1\right)}\left(k\right)w_{ri}^{\left(l+1\right)}\left(k\right)}\right)sg{m}^{\prime }\left(s_i^{\left(l\right)}\left(k\right)\right)$ (4.14)

és $N_{l+1}$ az (l+1)-edik réteg bemeneteinek száma.

Ha az l-edik réteg összes processzáló elemének súlyvektorait egy, az (1.6.) összefüggésben definiált $W^{\left(l\right)}$ mátrixba fogjuk össze, ahol tehát a mátrix i-edik sora az i-edik processzáló elem súlyvektora, akkor az l-edik réteg összes súlyvektorának módosítása tömören az alábbi formában adható meg:

$W_{}^{\left(l\right)}\left(k+1\right)=W_{}^{\left(l\right)}\left(k\right)+2\mu {\delta }^{\left(l\right)}{x}^{\left(l\right)}{}^T\left(k\right)$ . (4.15)

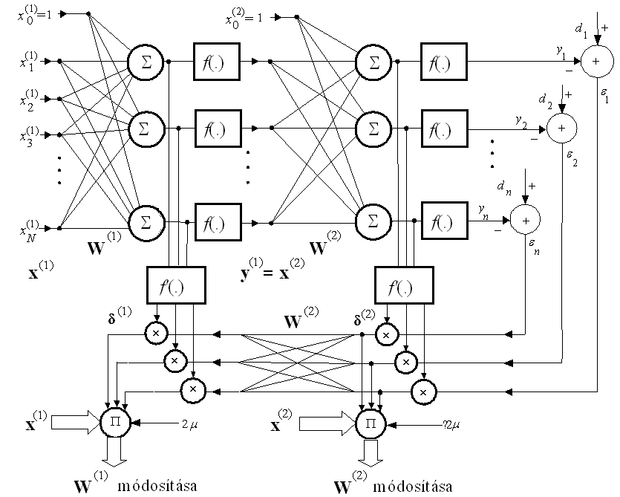
Itt ${\delta }^{\left(l\right)}$ a (4.14) összefüggéssel megadott ${\delta }_i^{\left(l\right)}$ visszaterjesztett "hibákból" képezett oszlopvektor. A súlymódosítást is tükröző hálózatarchitektúra két aktív rétegű hálózatnál a 4.2 ábrán látható. (Az ábrán a kimeneti nemlinearitást jelölő sgm helyett az általánosabb f(.) jelölés szerepel.)

Az előbbiekben bemutattuk a hibavisszaterjesztéses hálózat alapvető felépítését, működését. Az 1. fejezet approximációval foglalkozó részei pedig annak matematikai hátterét foglalták össze, hogy egy többrétegű, előrecsatolt hálózat egyáltalán milyen képességekkel rendelkezik. A hálózatok elvi alapjainak ismerete azonban még nem elegendő ahhoz, hogy e hálózatokat hatékonyan alkalmazni is tudjuk különböző gyakorlati feladatok megoldására. A következőkben azokkal a kérdésekkel foglalkozunk, melyek az elvi háttér birtokában most már azt is biztosítják, hogy a hálót hatékonyan tudjuk alkalmazni gyakorlati feladatok megoldására.