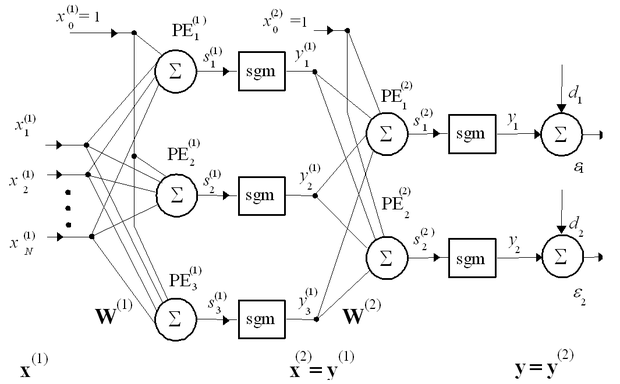
4.1. Az MLP felépítése
A többrétegű hálózatok felépítésea 4.1 ábrán követhető. Az ábra egy két aktív réteget tartalmazó hálózatot mutat, amelyben az első aktív rétegben − a rejtett rétegben − három, a második aktív rétegben − jelen esetben a kimeneti rétegben − két processzáló elem található. A hálózat tehát egy többrétegű előrecsatolthálózat. Az 1. fejezetben láttuk, hogy egy megfelelő méretű, többrétegű, szigmoid nemlinearitásokat tartalmazó hálózat − a súlyvektorok kialakítása után − tetszőleges folytonos nemlineáris függvény tetszőleges pontosságú approximációjára képes. A súlyvektorok meghatározása összetartozó tanítópont-párok felhasználásával ellenőrzött tanuló eljárással történik.
A háló bemutatásához vezessük be a következő jelöléseket: egy L információ-feldolgozást végző rétegből álló MLP-nél az egyes rétegeket felső indexszel (l=1, 2, …, L) különböztetjük meg. A rétegen belüli processzáló elemekhez (PE) az i indexet rendeljük, míg j a PE bemeneteit megkülönböztető index jelölésére szolgál − ez lesz egyben a megfelelő súlyvektor komponenseinek indexe is. (Pl. az l-edik réteg i-edik processzáló elemét, neuronját jelöli, ennek a neuronnak a súlyvektorát, míg ugyanezen súlyvektornak az j-edik komponensét jelöli.) A neuronok bemeneteire kerülő jeleket x-szel, a kimeneti jeleket y-nal jelöljük, szintén alkalmazva a réteg- és a rétegen belüli indexeket. Így pl. az l-edik neuronréteg i-edik processzáló elemének j-edik bemenetére kerülő jelet jelöli. A kimeneteknél megkülönböztetjük a súlyozott összegző kimenetét (lineáris kimenet) a neuron nemlineáris kimenetétől. A lineáris kimenetet az eddigi jelöléseknek megfelelően s-sel jelöljük. Egy MLP tetszőleges számú rejtett réteget használhat, és mint ahogy a hálók képességeit tárgyaló 1. fejezetben láttuk, ahhoz, hogy univerzális approximátor képességgel rendelkezzen, legalább egy szigmoid nemlinearitással rendelkező rejtett réteget kell tartalmaznia. A kimeneti réteg lehet lineáris, de lehet nemlineáris is. Az MLP bemutatásánál az általánosabb tárgyalás érdekében feltételezzük, hogy nemlineáris kimeneti réteget használunk.
A fenti felépítésnek megfelelően − összhangban az (1.6.) összefüggéssel − az MLP bemenet-kimenet leképezése − ha mindegyik nemlineáris rétegben azonos a nemlineáritás − a következő:
, (4.1)
ahol W(l) az l-edik réteg neuronjainak súlyvektorait összefogó mátrix, f(.) pedig az egy réteghez tartozó neuronok kimenetein értelmezendő szigmoid függvényeket jelöli. Egy MLP, még a legegyszerűbb esetben is, amikor csak egy rejtett réteget tartalmaz, paramétereiben nemlineáris leképezést valósít meg.
Az MLP tanítása ellenőrzött tanítás, ahol a hálózat kimenetén értelmezett hiba felhasználásával határozhatjuk meg a kritériumfüggvény vagy kockázat paraméterfüggését. Bár az MLP-nél is szinte kizárólag négyzetes hibafüggvényt szoktak alkalmazni, a nemlineáris paraméterfüggés miatt a hibafelület nem lesz kvadratikus. Mindössze abban lehetünk biztosak, hogy a hibafelület a tanítandó paraméterek folytonos, differenciálható függvénye, ami a gradiens alapú tanuló algoritmusok alkalmazását lehetővé teszi.
A következőkben az MLP-tanításánál leggyakrabban alkalmazott hibavisszaterjesztéses vagy back-propagation eljárást fogjuk bemutatni, ami szintén gradiens alapú tanító eljárás.