1.3. A neurális hálózatok alapvető számítási képességei, felhasználási területei
Az előbbiekben láttuk, hogy a neuronhálók a bemeneteik és a kimeneteik között általában valamilyen nemlineáris leképezést valósítanak meg. Egy statikus leképezésű elemi neuron ezért, mint elemi (nemlineáris) statikus rendszer kezelhető. Azt is láttuk, hogy megfelelő kiegészítésekkel, bővítésekkel az elemi neuron dinamikus működésűvé tehető. Egy neuronháló − amely tehát ilyen elemi neuronokból épül föl − úgy kezelhető, mint egy statikus vagy dinamikus (nemlineáris) rendszer, amelynek alkalmazhatósága attól függ, hogy milyen speciális képességekkel rendelkezik. Fontos kérdés tehát az egyes neuronháló architektúrák számítási képességeinek a meghatározása. Ebben a részben röviden ezt a kérdést vizsgáljuk, valamint kitérünk arra is, hogy ezeknek a képességeknek köszönhetően melyek a neuronhálók legfontosabb alkalmazási területei.
A neurális hálózatok képességeit és tulajdonságait a használt műveleti elemek tulajdonságai, a hálózat topológiája és a hálózat súlyainak értéke, − így közvetve a használt tanulási algoritmus − határozzák meg. A neuronhálók talán legfontosabb képessége, hogy megfelelő kialakítás esetén, szinte tetszőleges be-kimeneti kapcsolatot, leképezést meg tudnak valósítani, vagyis a szokásos elnevezés szerint ezek a neuronhálók ún. univerzális approximátorok. Az univerzális approximátor-képesség teszi lehetővé, hogy a neuronhálókat mint univerzális osztályozó és modellező eszközöket tekintsük. Az osztályozó/modellező képesség nagyon szerteágazó alkalmazási lehetőségeket biztosít, kiemelt fontosságú, ezért e kérdéssel részletesebben is foglalkozunk. Ugyanakkor ezek a hálózatok más nézőpontból asszociatív memóriaként viselkednek, ezért röviden erre is ki fogunk térni. Végül megemlítjük, hogy egyes neuronhálók hatékonyan alkalmazhatók bizonyos optimalizálási feladatok megoldásánál.
A megfelelő (statikus) bemenet-kimenet leképezés (függvénykapcsolat) előállítása központi feladat a mérnöki alkalmazások számos területén, pl. képfeldolgozásban, alakfelismerésben, osztályozási feladatokban, rendszer identifikációnál, szabályozástechnikában, jelfeldolgozásban stb. Ezért a neurális hálózatok igen fontos tulajdonsága, hogy a hálózatok számos típusa képes minták alapján a keresett leképezés közelítő, sok esetben tetszőleges pontossággal közelítő előállítására. Számos matematikai eredmény született a neurális hálók függvényapproximációs (valamilyen előírt leképezést közelítő) képességeivel kapcsolatban. Ezek az eredmények a terület jelentősége miatt nagymértékben növelték a neurális hálók iránti érdeklődést.
Kezdetben a neurális hálókat szinte kizárólagosan olyan feladatok megoldására használták, ahol a pillanatnyi bemenetre adott válasz nem függött sem az időtől, sem az előző bementi és/vagy kimeneti értékektől, tehát a megoldandó probléma statikus volt. A működés még akkor is statikus jellegű volt, mikor a kívánt választ csak valamilyen − időben lejátszódó − tranziens után érte el a hálózat, mivel nem a tranziens alakulása, hanem csak a végállapot jelenti a hálózat bemenetre adott válaszát.
A feladatok jelentős része viszont valamilyen dinamikát mutat: vagy maga a vizsgált folyamat (melyet optimalizálunk, vagy melynek az eredményeit osztályozzuk, stb.), esetleg a környezet (zaj, stb.) változik az időben (idővariáns folyamatok), vagy a folyamat pillanatnyi értéke nem csupán az adott bemeneti jeltől, hanem az előzményektől is függ. Ilyen feladattal találkozunk akkor is, ha egy időben változó értéksorozat valahány elmúlt értékének (egy időben változó folyamat régebbi mintavételi értékeinek) ismeretében a következő értéket vagy értékeket kell előre jelezni, jósolni (a későbbi mintavételi értékekre becslést adni). Ezeket a feladatokat idősor előrejelzési feladatoknak (time series prediction) szokás nevezni, és a legkülönbözőbb alkalmazási területeken, pl. komplex ipari rendszerek működésének, gazdasági és pénzügyi folyamatok viselkedésének, természeti jelenségek lefolyásának, időbeli alakulásának, stb. előrejelzésénél jelennek meg.
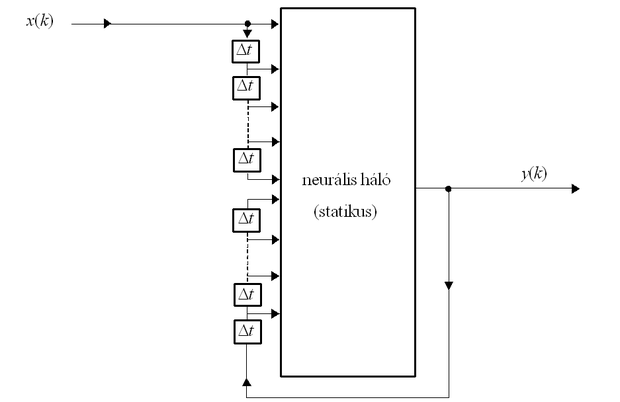
Természetesen ilyen esetekben a feldolgozó algoritmusnak vagy modellező eljárásnak is a megfelelő időfüggést kell mutatnia. Ezt neurális hálók alkalmazása esetén legtöbbször úgy érjük el, hogy a statikus feladatok megoldására kialakított (rendszerint nemlineáris) neurális hálót kiegészítjük dinamikus (rendszerint lineáris) komponensekkel. Több szinten történhet a dinamikus elemek felhasználása, pl. maga a neuron is dinamikussá tehető, mint ahogy azt az 1.1 illetve 1.6 ábrán bemutattuk. Dinamikus feladatok megoldásánál ugyanakkor gyakrabban alkalmaznak olyan megoldást, amikor a tisztán statikus hálót kiegészítik dinamikus komponensekkel. Erre számos lehetőségünk van. Ilyen lehetőséget mutat az 1.10 ábra, de az 1.8 (a) ábrán bemutatott visszacsatolt háló is egy statikus hálóból megfelelő visszacsatolás alkalmazásával előállított dinamikus rendszer.
Az 1.10 ábrán látható megoldásban a (statikus) neurális hálót bemeneti és kimeneti megcsapolt késleltető sorokkal (tapped delay line) egészítettük ki, így az aktuális kimeneti érték az előző be- és kimeneti értékektől is függ. Természetesen használhatunk összetettebb kiegészítő lineáris komponenseket is, mind a visszacsatoló, mind az előrecsatoló ágban.
Akármilyen módon alakítunk is ki dinamikus neurálisrendszereket, az alapvető problémát a hálózat tanítása jelenti. A tanítás rendszerint statikus esetben is lassú, nehézkes, dinamikus esetben pedig még ehhez képest is sokkal komplikáltabb, lassabb, sőt gyakran súlyos stabilitási problémákkal is meg kell küzdenünk.
Az approximációs képességhez számos matematikai eredmény kapcsolódik, melyeket fontosságuk miatt külön részben, az 1.4 alfejezetben foglalunk össze. A matematikai eredmények a statikus leképezésre vonatkoznak, azonban mint láttuk a dinamikus feladatok megoldására képes hálózatok is jórészt statikus neuronokon, statikus hálókon alapulnak, tehát a statikus leképezésre vonatkozó eredmények adják meg annak is a matematikai alapját, hogy megfelelő architektúrájú neuronhálókkal dinamikus feladatokat is hatékonyan meg tudunk oldani.
A neurális hálók definíciójából is látható, hogy egy neuronháló egy speciális memóriaként is felfogható, melybe meghatározott módon (tanulás, learning ) információt írunk be, s ezt később visszaolvassuk (előhívás, recall ). Az általánosan használt írható/olvasható (RAM) memóriáknál az adat kiválasztott címre való beírását tekinthetjük tanulásnak, az előhívási algoritmus során pedig a címinformációt használjuk bemeneti jelként, melyre válaszként a tárolt adatot kapjuk meg. Ezzel szemben a neurális hálózatokat, mint adattal címezhető memóriát (content addressable memory), vagy mint asszociatív memóriát (associative memory) használjuk.
Adattal címezhető memória esetén a tanulás során a tanítási adathalmaz elemeit kapcsoljuk a hálózat bemenetére, s a hálózat autonóm vagy felügyelt módon azonos címhez (azaz a háló kimenetéhez) igyekszik hozzárendelni az összetartozó adatokat. Az előhívási fázisban is adatokat kapcsolunk a hálózat bemenetére, s a visszanyert információt az hordozza, hogy a megtanult címek közül melyiket adja vissza a hálózat. (Pl. ha osztályozási feladatot tanítunk, sikeres tanulás eredményeképp az azonos osztályba tartozó bemeneti adatok azonos, vagy egymáshoz közeli címeket adnak a kimeneten, míg a különböző osztályba tartozó bemeneti minták távoli címeket adnak.)
Asszociatív memóriaként alkalmazva a neurális hálót összetartozó adatpárokat használunk, s a hálózatot arra tanítjuk, hogy az adott bemeneti adathoz a megfelelő kimeneti adatot rendelje hozzá. Az előhívás során adatot használunk bemenetként, és válaszként is egy − a bemenetihez kapcsolt, asszociált − adatot kapunk. (Pl. itt említhetjük a jelfeldolgozási feladatokat, mikor a bemeneti jelhez egy szűrt/módosított kimeneti jel tartozik.)
Az asszociáció két változatát, az autoasszociációt és a heteroasszociációt szokás megkülönböztetni. Autoasszociatív (autoassociative) hálóról akkor beszélünk, ha a tanítás során a neurális háló a bemenetére kapcsolt jelvektorokat, mintákat tárolja abból a célból, hogy a későbbiek során, ha a háló bemenetére a megtanított minták részleges vagy torzított (zajos) változatai kerülnek, a háló az eredeti, teljes, zajmentes mintát adja vissza válaszként a kimenetén. Ezek a hálók a bemeneti mintákat önmagukkal asszociálják. Autoasszociatív hálót használhatunk akkor is, ha adott jelek hatékony közelítő reprezentációját akarjuk előállítani. A háló ilyenkor olyan közbenső, közelítő reprezentációt állít elő, melyből maga a háló próbálja visszaállítani az eredeti jelet. A heteroasszociatív (heteroassociative) hálóknál a bemeneti vektorokhoz, mintákhoz tetszőleges kimeneti vektorok kapcsolhatók. A háló tehát összetartozó párokat kell, hogy eltároljon, és tanítás után egy megadott bemenetre a hozzátartozó kimenetet kell válaszként előállítania, vagyis egy bemeneti mintát egy tetszőleges, de a bemeneti mintához párosított mintával asszociálja.
Általánosságban mind a bemeneti, mind a kimeneti minta lehet egy-egy mintaszekvencia is. Az ilyen összerendelésekre a dinamikus hálók képesek. A dinamikus hálók tehát mint bemeneti adatszekvenciákhoz kimeneti adatszekvenciákat asszociáló asszociatív memóriák is értelmezhetők.
Az optimalizálás a mérnöki tevékenység egyik alapvető lépése. Optimalizálás során általában valamilyen költséget kívánunk minimalizálni, a rendszer struktúrájának, illetve paramétereinek megfelelő megválasztásával. Nem feltétlenül klasszikus, pénzben kifejezhető költségre kell gondolnunk, költségként jelentkezhet a szükséges számítási kapacitás, a számítási idő, a memória igény, a modellezési hiba, stb. Általában egy költségfüggvénynek két fontos jellemzője van, egyrészt minden megoldáshoz egyértelműen hozzárendel egy skalár mennyiséget, másrészt ez a skalár mennyiség kifejezi a megoldás − valamilyen szempontból értelmezett − jóságát. Egy tipikus példa, ha egy gyártási folyamat során elvégzendő feladatokat akarjuk egy gépcsoporttal (melyben a gépek eltérő sebességgel azonos, illetve különböző részműveletek elvégzésére képesek) úgy megoldani, hogy a műveletek összes idejét, plusz a várakozási időket minimalizáljuk. Az optimalizálási feladat során azt keressük, hogy mely gépekhez mely részműveleteket milyen sorrendben kell hozzárendelnünk.
Neurális hálózatokat sikerrel alkalmaztak bizonyos optimalizálási feladatok megoldásában is. A megoldás menete általában az, hogy egy, a minimalizálni kívánt költséget kifejező skalár függvényt keresünk − a fenti példában az összidő lehet ilyen függvény −, ezután olyan hálózatot hozunk létre, melynek paramétereihez egyértelműen hozzárendelhető a költségfüggvény. (Pl. egy-egy neuron megfelel egy-egy részműveletnek, illetve gépnek, a részműveletet reprezentáló neuron kimenetét a használt géphez kapcsoló súly értéke pedig az adott műveleti idő és várakozási idő összege.) Az optimalizációs feladatokra alkalmas hálók többnyire visszacsatolt struktúrájúak, ami azt jelenti, hogy a háló valamely kiinduló állapotból egy tranziens során jut el egy végállapotba. Amennyiben a hálózatot úgy tudtuk kialakítani, hogy tetszőleges állapotból indítva, a lejátszódó tranziens során a költségfüggvény minden lépésben csökkenjen, akkor a végállapot valamilyen költségminimumot reprezentál.
A neuronhálókkal megoldott optimalizációs feladatokra általában az a jellemző, hogy a kapott megoldás nem feltétlenül biztosítja, hogy a globális költségminimumot, tehát az optimumot elérjük. Bonyolult problémák esetén azonban sokszor megelégszünk azzal is, ha az optimum helyett egy „jó” megoldást találunk. Különösen akkor igaz ez, ha az optimalizálási feladat komplexitása miatt a valódi optimum elérése nem reális, miközben egy neuronháló alapú „jó” megoldás kis számításigénnyel is elérhető. Tipikusan ilyenek a kombinatorikus optimalizálási feladatok, melyek között számos NP-teljes problémát találunk.