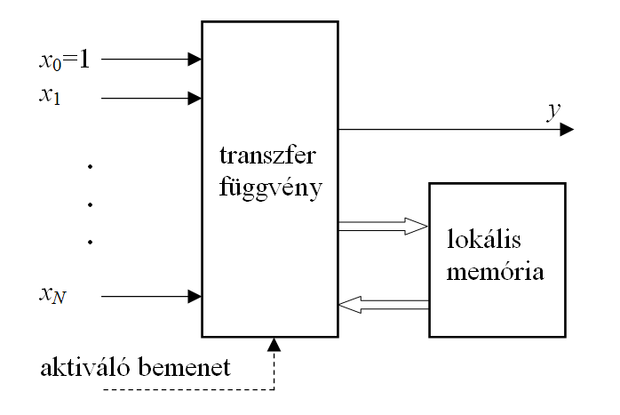
Egy neuron vagy műveleti elem, processzáló elem (processing element) egy több-bemenetű, egy-kimenetű eszköz, amely a bemenetek és a kimenet között általában valamilyen nemlineáris leképezést valósít meg. Egy neuron rendelkezhet lokális memóriával is, amelyben akár bemeneti, akár kimeneti értékeket vagy a működés előéletére vonatkozó állapotinformációt tárolhat. A bemeneti- vagy a bemeneti- és a tárolt értékekből az aktuális kimeneti értéket egy tipikusan nemlineáris függvény alkalmazásával hozza létre, melyet aktiváló vagy aktivációs függvénynek nevezünk (activation function). (Használnak egyéb magyar és angol elnevezéseket is, mint pl. neuron esetén feldolgozó elem, vagy csomópont (node); aktivációs függvény esetén pl. transzfer függvény (transfer function).

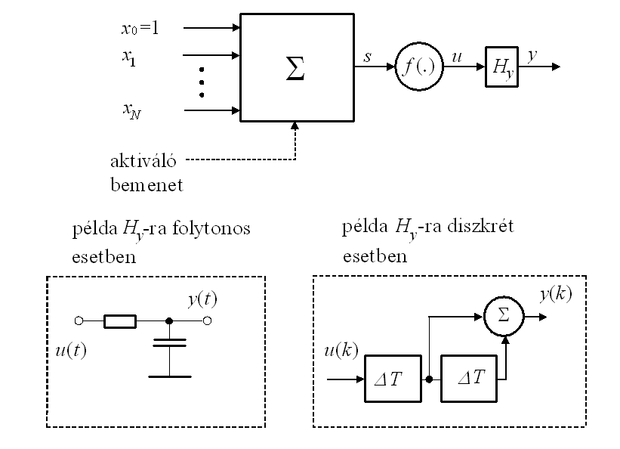
A neuronok rendelkeznek változó értékeket (a hálózat bemeneti jelei, más neuronok kimeneti jelei) hordozó bemenetekkel, illetve rendelkezhetnek állandó értéket hordozó bemenettel, pl. ilyen az 1.1 ábrán x₀. Az ábrán kitüntetett szerepű aktiváló bemenet diszkrét idejű működés esetén a hálózat ütemezését vezérli, folytonos idejű működés esetén elmarad. A neuron működését az alábbi matematikai formában adhatjuk meg (diszkrét idejű hálózatra, ahol k az időlépés indexe):

$\text{y(k)}=\text{f(}x\text{(k)},x\text{(k}-\text{1)}\mathrm{,...,}x\text{(k}-M\text{)},\text{y(k}-\text{1)}\mathrm{,...,}\text{y(k}-L\text{))}$ (1.1)

ahol $x\text{(}k\text{)}={\text{[}{x}_0\text{(}k\text{)},x_1\text{(}k\text{)}\mathrm{,...,}{x}_N\text{(}k\text{)]}}^T$ . Az áttekinthetőség kedvéért az N változó- és az egyetlen konstans bemenetet egy N+1 elemű x vektorba fogtuk össze. Ebben az esetben a neuron egy $f:{ℝ}^{\left(M+\text{1}\right)\left(N+\text{1}\right)+L}\to ℝ$ leképezést valósít meg.

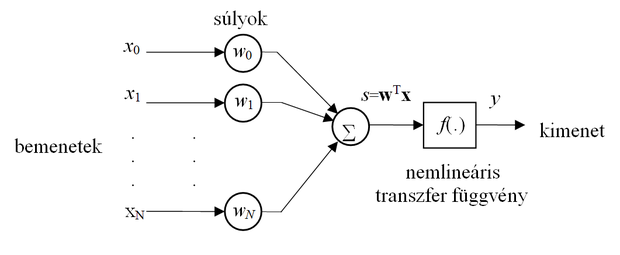
A fenti általános felépítést az alábbiakban néhány fontos, elterjedt esetre konkretizáljuk. A műveleti elemek legegyszerűbb és egyben legelterjedtebb változata az egyenrangú bemenetekkel rendelkező memória nélküli neuron, melynek tipikus felépítése az 1.2 ábrán látható. A bemutatott neuron esetén az x_i skalár bemenetek w_i (i=0,1,...,N) súlyozással kerülnek összegzésre, majd a súlyozott összeg egy f(.) nemlineáris elemre kerül. Szokás az 1.2 ábrán látható neuronok esetén a bemeneti jelek súlyozott összegét (az összegző hálózat s kimeneti jelét, mely a nemlinearitás bemenete) ingernek (excitation), míg a kimeneti jelet válasznak (activation) nevezni. Ezek az elnevezések az egyes területeken ma is erősen hivatkozott biológiai analógiára utalnak.

Egyes neuronhálóknál a nemlineáris transzfer függvény elmarad, így lineáris neuronokról is beszélhetünk. Az ilyen lineáris súlyozott összegzőt megvalósító neuront önmagában viszonylag ritkán használják, legtöbbször egy nagyobb hálózat kimeneteinek előállítására szolgál. Vannak azonban olyan nemellenőrzött tanítású hálók, amelyek lineáris neuronokból épülnek fel. Ezeknél a hálóknál a speciális tulajdonságot a súlyok kialakítása, a speciális tanulási eljárás biztosítja.

A hálózat összegző pontján a bemenetek lineáris kombinációját kapjuk

$s\text{=}{\displaystyle \sum _{i\text{=}0}^N{w}_i{x}_i}\text{=}{w}^{T}x$ . (1.2)

A memória nélküli neuronok lineáris változata esetén az összegző kimenete közvetlenül a neuron kimenetét is jelenti:

$y=s=w^{T}x$ (1.3)

Az 1.2 ábrán bemutatott, összegzővel sorbakapcsolt nemlinearitást használó egyszerű felépítésű neuront perceptron néven Frank Rosenblatt [Ros58], illetve adaline néven Bernard Widrow [Wid60] javasolta. A két neuron-modell felépítése megegyezik, eltérés csupán az alkalmazott tanítási eljárásokban van, melyeket a 3. fejezetben mutatunk be. Mind az adaline, mind a Rosenblatt-perceptron által megvalósított leképezést a (1.4) összefüggés adja meg:

$y=f\text{(}s\text{)=}f\left(w^{T}x\right)$ . (1.4)

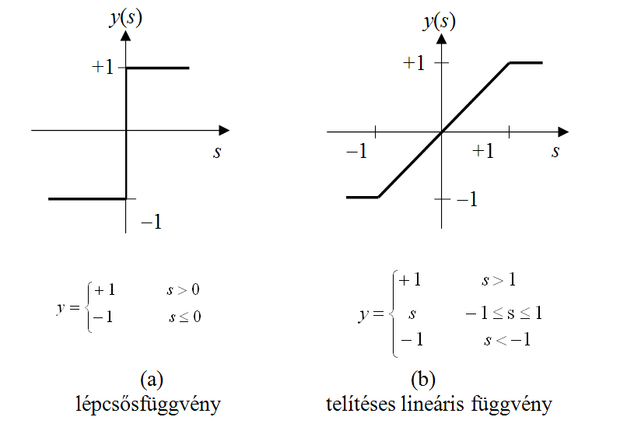
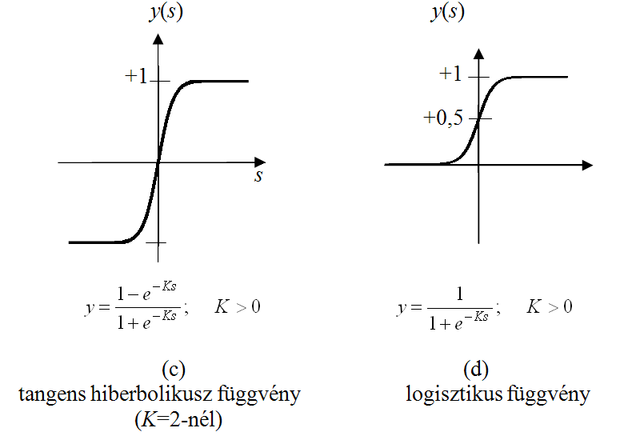
A nemlineáris aktivációs függvény tipikusan küszöbfüggvény jellegű leképezés, melynek értelmezési tartománya általában a valós számok halmaza, értékkészlete pedig a valós számok egy korlátos részhalmaza. Négy legelterjedtebb változata az 1.3 ábrán látható. Az első (a) az ugrásfüggvény, a második (b) a telítéses lineáris függvény, a harmadik (c) és negyedik (d) folytonos, monoton növekvő, telítődő jellegű függvények, melyeket a szigmoid függvényeknek nevezünk. A szigmoid függvényeknek kitüntetett szerepük van a neuronhálóknál. Két leggyakoribb megvalósítási formájuk a tangens hiperbolikusz és a logisztikus függvény.

Egyes estekben a neuron bemeneteit csoportokba osztjuk aszerint, hogy a bemeneti jel a neuron kimenetén a válaszjelet növeli, vagy csökkenti. Ezeket a bemeneti jelcsoportokat a biológiai analógia alapján gerjesztő (excitory inputs), illetve gátló (inhibitory inputs) bemeneteknek nevezzük. A gerjesztő és gátló bemenetekkel is rendelkező memória nélküli neuronokra példa a Fukushima által képfeldolgozásra javasolt típus [Fuk88].

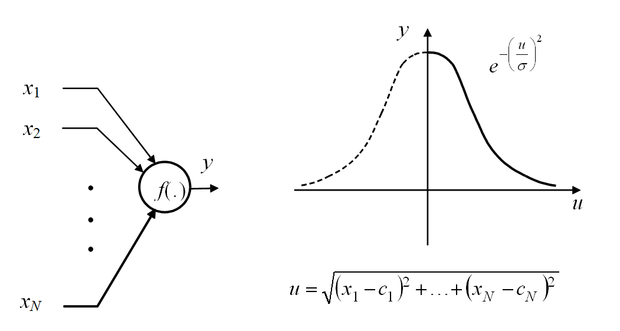
A memória nélküli neuronok másik típusát kapjuk, ha az 1.4 ábrán látható struktúra azon speciális változatát használjuk, mikor minden bemenet közvetlenül a nemlineáris elemre jut, azaz a nemlineáris aktivációs függvény előtt elmarad az összegzés, viszont nem egybemenetű, hanem N-bemenetű a nemlinearitás. Ennek elterjedt és napjainkban nagy jelentőségű típusa az RBF (Radial Basis Function) hálózatban használt neuron, de ebbe a csoportba sorolható az összes többi bázisfüggvényes hálózat is. A bázisfüggvényes hálózatokra jellemző még, hogy általában maga a bázisfüggvény is tartalmaz paramétereket, melyeket a háló konstrukciójakor valamilyen módon meg kell határozni.

Az 1.4 ábrán látható, hogy a kimenet tulajdonképpen a bemeneti vektor, x=[x₁, x₂ , . . ., x_N]^T és egy, a neuronra jellemző c=[c₁, c₂, . . . , c_N]^T középpont-vektor távolságának nemlineáris függvénye. Az ábrán az euklideszi távolságdefiníciót használtuk, de nincs akadálya egyéb távolságfogalmak bevezetésének és használatának sem. A legelterjedtebb esetben Gauss függvényt használunk nemlinearitásként, melynek c középpont-vektora mellett paramétere még a függvény szélességét meghatározó σ is.

Az 1.5 ábrán egy a kimenetén $H_y^{}$ lineáris dinamikus hálózattal (lineáris szűrővel) kiegészített (eredetileg) memória nélküli neuron látható. Az ábrán mind folytonos, mind diszkrét idejű esetre egy-egy konkrét, egyszerű dinamikus hálózatot is felrajzoltunk, csupán a szemléltetés kedvéért. (Ezek ebben a formában nem feltétlenül használhatók.)

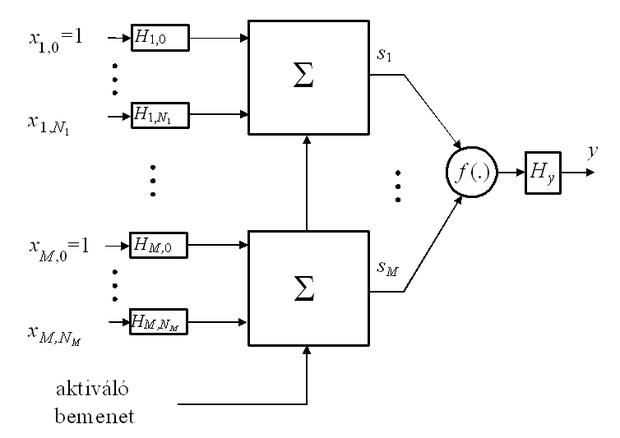
Az ábrán látható eset kiegészíthető bemeneti lineáris szűrőkkel is, illetve kiterjeszthető több-bemenetű nemlinearitásra is, így egyre bonyolultabb modelleket nyerhetünk. (Természetesen míg a bonyolultabb modell komplexebb problémákra alkalmazható, addig megvalósítási, stabilitási, konvergencia stb. gondokat vethet fel.) Bonyolultabb esetre példa az 1.6 ábrán látható, memóriával és M-bemenetű aktivációs függvénnyel rendelkező neuron, mely képes az 1.1 ábrán látható általános műveleti elemmel kialakítható legtöbb funkció megvalósítására. A neuronstruktúrája azonban kötöttebb, mint az 1.1 ábrán látható esetben. A tárolási funkció itt is a neuron bemenetén és kimenetén felépített lineáris dinamikus rendszerekben valósul meg. (Implementációs előnyt jelenthet, ha az összegzők kimenetén − az s₁,…,s_M jelek szűrésére − valósítjuk meg a lineáris szűrőket, ezek azonban az összegzők bemenetére transzformálhatók, így az elvi áttekintésre elég az 1.6 ábrán látható struktúra.) Diszkrét idejű hálózatokban attól függően, hogy a neuronban használt szűrőhálózatok véges impulzusválaszúak (finite impulse response, FIR szűrők), vagy végtelen impulzusválaszúak (infinite impulse response, IIR szűrők) FIR neuronokról vagy IIR neuronokról beszélünk [Wan90]; [Lei91]. Természetesen nincs akadálya egyéb kombinációk kialakításának, pl. a bemeneten FIR, a kimeneten IIR szűrőket használó változatnak sem.

A neurális hálózatban használt összeköttetések egyirányú jelterjedést biztosítanak a hálózat bemenete vagy egy neuron kimenete felől egy neuron bemenete vagy a hálózat kimenete felé. Egy kimenet több (általában tetszőleges számú) bemenettel köthető össze, ekkor valamennyi bemenet ugyanazt a jelet kapja. Kimeneteket egymással nem köthetünk össze. Az összeköttetések késleltetés nélküliek (az esetleges késleltetéseket szűrővel modellezhetjük a neuron bemenetén).

Elsősorban az 1.2.1 fejezetben tárgyalt memória nélküli neuronoknál a bemeneti súlytényezőket gyakran az aktuális bemenetekhez vezető összeköttetésekhez rendelik, nem a neuronhoz. Ez semmilyen elvi különbséget sem jelent.

A hálózat topológiáján a neuronok összeköttetési rendszerét és a hálózat bemeneteinek és kimeneteinek helyét értjük. A hálózat topológiáját általában irányított gráffal reprezentáljuk. A gráf csomópontjai a neuronoknak felelnek meg, míg a kapcsolatokat a kimenetek és bemenetek között a gráf élei reprezentálják, a neuron-bemenettől a kimenet felé irányítva. (Az élekhez értelemszerűen hozzárendelhetjük a megfelelő w_ij bemeneti súlytényezőket vagy a H_ij(z^-1) szűrőket, ld. 1.2.1 alfejezet.)

A gráf egyes csomópontjai rendszerint nincsenek az összes többi csomóponttal kapcsolatban, csupán a csomópontok egy részhalmazával. Ez legtöbbször lehetőséget nyújt arra, hogy a gráf csomópontjainak − a neuronoknak − halmazát diszjunkt részhalmazokra bontsuk. Ennek megfelelően háromféle neuront különböztethetünk meg:

A neuronokat sok esetben rétegekbe (layers) szervezzük, ahol egy rétegbe hasonló típusú neuronok tartoznak. Az egy rétegbe tartozó neuronokra még az is jellemző, hogy kapcsolataik is hasonlók. Az azonos rétegbe tartozó neuronok mindegyikének bemenetei a teljes hálózat bemenetei, vagy egy másik réteg neuronjainak kimeneteihez kapcsolódnak, kimenetei pedig ugyancsak egy másik réteg neuronjainak bemeneteit képezik, vagy a teljes hálózat kimeneteit alkotják. Ennek megfelelően beszélhetünk bemeneti rétegről (input layer), rejtett réteg(ek)ről (hidden layer(s)) és kimeneti rétegről (output layer). A bemeneti réteg, amely buffer jellegű neuronokból épül fel, információfeldolgozást nem végez, feladata csupán a háló bemeneteinek a következő réteg bemeneteihez való eljuttatása. Ennek megfelelően egy rétegekbe szervezett háló legalább két réteggel, egy bemeneti és egy kimeneti réteggel kell rendelkezzen. E két réteg között elvben tetszőleges számú rejtett réteg helyezkedhet el.

A szakirodalomban a rétegszám definíciója sokszor nem egyértelmű. Egyes szerzők a rendszerint lineáris, bemeneti buffer réteget is beleszámítják a rétegszámba, mások csak a rejtett- és kimeneti rétegeket, tehát csak azokat a rétegeket, melyek információfeldolgozást is végeznek. Így az egyértelműség kedvéért az a szokás terjedt el, hogy az aktív, jelfeldolgozást is végző (processzáló) rétegek számát adják meg a hálózat jellemzőjeként.

A neuronhálókat az egyes neuronok közötti összeköttetési rendszer alapján két fő csoportba sorolhatjuk: beszélhetünk előrecsatolt hálózatokról (feedforward networks) és visszacsatolt hálózatokról (recurrent networks). Visszacsatoltnak nevezünk egy neurális hálót, ha a topológiáját reprezentáló irányított gráf tartalmaz hurkot, egyébként a neurális háló előrecsatolt. Előrecsatolt hálóra mutat példát az 1.7 és az 1.8 (b) ábra, míg egy visszacsatolt architektúra az 1.8 (a) ábrán látható.

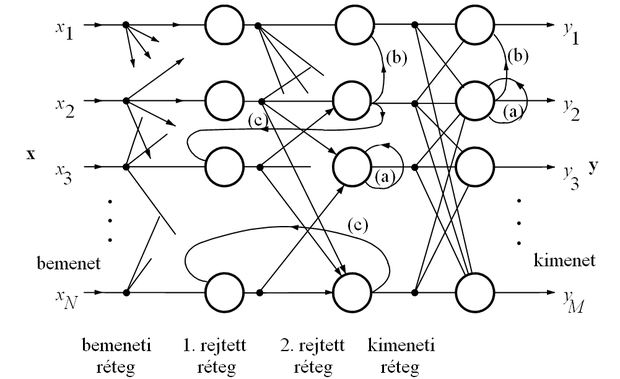
A visszacsatolt hálózatoknál beszélhetünk globális és lokális visszacsatolásról. Globális visszacsatolásnál a hálózat kimenetét csatoljuk vissza a bemenetére. A lokális visszacsatolásokat három csoportba sorolhatjuk (1.9 ábra):

A jobb áttekinthetőség kedvéért az 1.9 ábrán a visszacsatolásokon kívül csak néhány további összeköttetést jelöltünk.

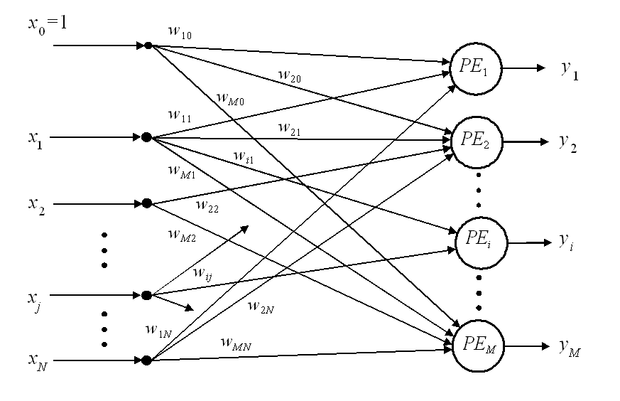
A legegyszerűbb, memória nélküli neuronokból (ld. 1.2 ábra) felépített egy processzáló rétegű előrecsatolt hálózatnak (1.7 ábra) egy bemeneti buffer rétege és egy feldolgozó rétege van, mely egyben a kimeneti réteg is. A hálózat N bemenettel és M kimenettel (M információfeldolgozást végző neuronnal, processzáló elemmel, PE) rendelkezik. Mind a bemeneteket, mind a neuronokat sorszámmal láttuk el. Az 1 ... N sorszámú bemenetek a bemeneti réteget adják, a PE_i-vel jelölt neuronok a kimeneti réteget, ahol i=1,…,M. Ehhez kapcsolódik még a szokásos konstans értéket biztosító, az ábrán 0 sorszámmal jelölt bemenet. Természetesen itt az 1.2 ábrához képest − a több neuron miatt − a processzáló réteg bemeneti súlyait kettős indexeléssel látjuk el, az első index a neuronra, míg a második a neuronhoz kapcsolódó bemeneti komponensre utal.

Az 1.7 ábrán látható hálózat átvitele az (1.2) és az (1.3) összefüggések, (nemlineáris aktivációs függvény esetén az (1.4) összefüggés) alapján felírható. Értelemszerűen a súlyvektor helyét a súlyokból képzett W mátrix veszi át, a kimeneten pedig az y vektort kapjuk. Az alábbi összefüggés a nemlineáris aktivációs függvény esetét mutatja:

$y=f\text{(}s\text{)}=f\text{(}Wx\text{)}$ $$ (1.5)

(Megjegyezzük, hogy az (1.5) összefüggés a szokásosnál általánosabb kapcsolatot is megenged s és y között. A legtöbb esetben ugyanis az f(.) leképezés az s vektor komponenseire hat és így állítja elő y komponenseit.)

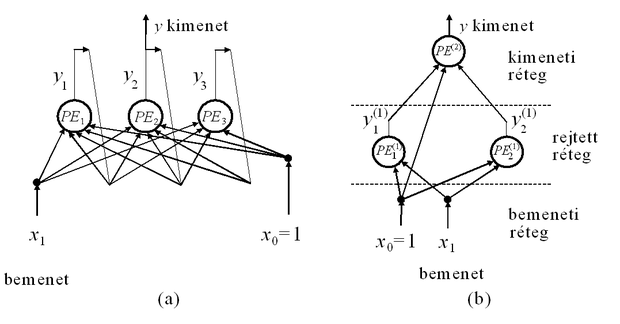
Az 1.8 ábrán egy teljesen összekötött topológiájú visszacsatolt hálózat és egy rétegekbe szervezett topológiájú egybemenetű-egykimenetű, előrecsatolt hálózat látható, mindkettő 3 ‑ 3 neuronból áll. A második háló a fentiek értelmében egy kétrétegű (két processzáló rétegű) vagy másképpen egy rejtett rétegű hálózat. Az ábrán az információfeldolgozást végző neuronokat ismét $P{E}_i^{\text{(}l\text{)}}$ -vel jelöltük, ahol a felső index a rétegindex, az alsó pedig a rétegen belüli sorszám. Az egyes neuronok kimenetei − a többrétegű esetben − a neuronok jelöléséhez hasonlóan ugyancsak két indexet kaptak. A felső a rétegindex, az alsó a rétegen belül a sorszámot adja meg. (Hogy a későbbiek során a felső index ne legyen összetéveszthető a hatványkitevővel, a felső indexet minden esetben zárójelbe tesszük.) Az ábrán az áttekinthetőség érdekében a súlyokat nem jelöltük, de a bevezetett konvenciónak és annak megfelelően, hogy a súlyokat neuronokhoz rendeljük, általánosságban az l-edik réteg i-edik neuronjának a j-edik bemenetéhez kapcsolódó súlyát $w_{ij}^{\text{(}l\text{)}}$ fogja jelölni.

A neurális hálók − elsősorban a rétegekbe szervezett memória nélküli hálók − topológiáját nemcsak gráf reprezentációval adhatjuk meg, hanem az egyes rétegek közötti összeköttetést mátrixok segítségével is leírhatjuk.

Előrecsatolt hálóknál (pl. 1.8 (b) ábra) ez értelemszerűen azt jelenti, hogy az 1.5 összefüggéshez hasonlóan az egyes rétegek neuronjaihoz tartozó súlyok egy mátrixba foghatók össze, ahol a mátrix egyes sorai az egyes neuronok súlyaiból képezett vektorok. $W^{(l)}$ tehát az l-edik rétegben lévő neuronok súlyaiból, mint sorvektorokból képzett mátrix. Egy többrétegű, előrecsatolt háló egyes rétegei által megvalósított leképezés tehát, ha összeköttetések csak a szomszédos rétegekben lévő neuronok között vannak, a következő formában adható meg:

_$$ $y^{\text{(}l\text{)}}=f\text{(}{s}^{\text{(}l\text{)}}\text{)}=f\text{(}{W}^{\text{(}l\text{)}}{y}^{\text{(}l\text{-1)}}\text{)}$ (1.6)

Egy két rejtett réteggel rendelkező hálózat bemeneti-kimeneti leképezése ennek megfelelően:

$y=f\left(W^{\text{(2)}}f\left(W^{\text{(}1\text{)}}x\right)\right)$ (1.7)

Itt $W^{(1)}$ illetve $W^{(2)}$ rendre az első és a második aktív (rejtett) réteg súlyait tartalmazó mátrix, az f(.) függvényt komponensenként kell érteni. Az 1.8 (b) ábrán látható hálózatnál $W^{(1)}$ egy 2×2-es mátrix, míg $W^{(2)}$ egy 3 elemű vektor:

$\begin{array}{c}{W}^{\text{(1)}}\text{ =}\left[\begin{array}{cc}{w}_{10}^{\text{(}1\text{)}}& w_{11}^{\text{(}1\text{)}}\\ w_{20}^{\text{(}1\text{)}}& w_{21}^{\text{(}1\text{)}}\end{array}\right]\\ \\ W^{\text{(2)}}\text{ =}\left[w_{10}^{\text{(}2\text{)}}{w}_{11}^{\text{(}2\text{)}}{w}_{12}^{\text{(}2\text{)}}\right]\end{array}$ (1.8)

A súlyok mátrixos formában történő felírása természetesen visszacsatolt hálóknál is lehetséges, hiszen a súlyok itt is neuronok bemeneteihez kapcsolódnak. A konkrét összeköttetési rendszer szabja meg, hogy az egyes neuronok honnan kapnak bemenetet; visszacsatolt hálózatoknál általában mind közvetlen bemenetek, mind visszacsatolt kimenetek is szerepelnek bemenetként. Visszacsatolt hálóknál természetesen figyelembe kell venni, hogy a visszacsatolt hálók dinamikus működést valósítanak meg, és hogy egy neuronon a jeláthaladás késleltetéssel jár. Diszkrét idejű hálózatot feltételezve ez azt jelenti, hogy egy visszacsatolt háló kimenete a k-adik időpillanatban a bemeneteinek a (k−1)-edik időpillanatbeli értékeitől függ. Például az 1.8 (a) ábrának megfelelő egy neuronrétegből álló visszacsatolt hálózat leképezésének általános formája

$y\text{(}k\text{) = }f\text{(}Wu\text{(}k-1\text{))}$ (1.9)

ahol u a neuronok összes bemenetét tartalmazó vektort jelöli. Az ábrának megfelelő konkrét hálózatnál a kimenet skalár, a bemeneti vektor pedig mind közvetlen bemeneti komponensekből, mind visszacsatolt kimenetekből áll:

$y\left(k\right)=y_2\left(k\right)\text{és}u\left(k\right)={\left[x_0\left(k\right),x_1\left(k\right),y_1\left(k\right),y_2\left(k\right),y_3\left(k\right)\right]}^T$ (1.10)