Az eddigiekben láttuk, hogy egy előrecsatolt, rétegekbe szervezett neuronokból felépülő neuronháló a bemenetei és a kimenetei között valamilyen (nemlineáris) leképezést valósít meg. E neuronháló-család alkalmazási körét az határozza meg, hogy a hálók által megvalósított leképezések milyen jellegű függvénykapcsolattal írhatók le. Precízebb megfogalmazásban arra keressük a választ, hogy egy előrecsatolt többrétegű hálózat által megvalósítható leképezés milyen függvényosztályba tartozó y=f(x) függvényeket tud pontosan előállítani, vagy legalább valamilyen értelemben közelíteni. E hálók számítási képessége a függvényapproximáció témakörének speciális szelete.

1900-ban a híres német matematikus, David Hilbert (1862-1943) 23 érdekes matematikai problémát fogalmazott meg, melyek megoldása véleménye szerint a XX. század matematikusainak fontos feladata lesz. A felsorolt problémák között a 13. volt az a sejtés, melynek eredeti alakja mérnöki szemmel nézve meglehetősen érdektelennek tűnik [Lor76]:

"Bizonyítsuk be, hogy az x⁷+ax³+bx²+cx+1=0 hetedfokú egyenlet nem oldható meg pusztán kétváltozós függvények segítségével!"

Hilbert 13. problémájának más matematikusok által adott átfogalmazása már számunkra is több érdekességet mutat:

"Mutassuk meg, hogy van olyan háromváltozós folytonos függvény, mely nem írható fel véges számú kétváltozós folytonos függvény segítségével!"

Ez a megfogalmazás ugyanis számunkra azt jelenti, hogy vannak olyan (nemlineáris) hárombemenetű rendszerek, melyek nem dekomponálhatók egy- vagy kétbemenetű rendszerek segítségével. Mivel a bonyolult problémák mérnöki megközelítése igen gyakran az egyszerűbb rendszerekre való dekompozíció, ha Hilbert sejtése igaznak bizonyul, akkor ezen rendszerek megvalósíthatósága várhatóan igen súlyos nehézségekbe ütközik.

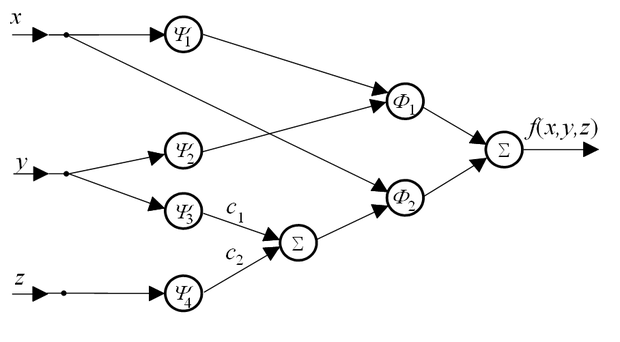
Itt a kétváltozós függvényeket részint szuperpozícióban használhatjuk, illetve megengedett a függvény-függvénye struktúra használata is. Például a ${\varphi }_{\text{1}}\left(\mathrm{.,.}\right)$ és a ${\varphi }_2\left(\mathrm{.,.}\right)$ kétváltozós és a ψ₁(.),ψ₂(.),ψ₃(.),ψ₄(.) egyváltozós függvények felhasználásával a háromváltozós f függvénynek ebben az értelemben legális felírása az alábbi:

$f\text{(}x\text{,}y\text{,}z\text{)=}{\varphi }_1\left({\psi }_1\text{(}x\text{)}\text{,}{\psi }_2\text{(}y\text{)}\right)\text{+}{\varphi }_2\left(c_1{\psi }_3\text{(}y\text{)+}{c}_2{\psi }_4\text{(}z\text{)}\text{,}x\right)$ (1.11)

A fenti összefüggés tulajdonképpen egy neurális háló struktúrával megvalósítható leképezést takar (ld. 1.11 ábra), ahol a bemeneten használt lineáris buffer neuronok mellett összegző és kétbemenetű nemlineáris neuronokat használunk, a neuronok aktivációs függvényei pedig rendre az összefüggésben használt egyváltozós függvények.

A helyzet a neurális hálókkal való approximáció szempontjából akkor vált igazán érdekessé, mikor 57 évvel később Andrej Kolmogorov (1903-1987) megcáfolta a Hilbert sejtést, és bebizonyította, hogy nem csupán minden háromváltozós függvény, hanem tetszőleges N-változós folytonos függvény felírható csupán egyváltozós függvények és az összeadás segítségével. (Érdekességként megemlítjük, hogy Kolmogorov és Vladimir Arnold versenyeztek egymással Hilbert 13. problémájának megoldásában, egyre újabb és újabb eredményeket értek el az 50-es évek során, míg 1957-ben Kolmogorov bebizonyította az eredeti Hilbert sejtés cáfolatán messze túlmutató reprezentációs tételét.)

1.1 tétel [Kol57]

Minden N≥2 egész esetén található N(2N+1) olyan folytonos, monoton növekvő, egyváltozós, az I=[0,1] intervallumon értelmezett ${\psi }_{pq}$ függvény, melyek segítségével tetszőleges N változós, valós, folytonos $f:{\text{ I}}^N={\left[\mathrm{0,}\text{1}\right]}^N\to ℝ$ függvény az alábbi alakban előállítható

$f\text{(}{x}_1\text{,}{x}_2\mathrm{,...,}{x}_N\text{)=}{\displaystyle \sum _{q\text{=1}}^{2N+1}{\varphi }_q}\left({\displaystyle \sum _{p=1}^N{\psi }_{pq}\text{(}{x}_p\text{)}}\right)$ (1.12)

Az összefüggésben felhasznált ${\varphi }_q(.)$ q=1,...,2N+1 egyváltozós függvények különböző f-ek esetén különbözőek, de a ${\psi }_{pq}(.)$ p=1,...,N; q=1,...,2N+1 egyváltozós függvények csak N értékétől függenek (minden f-re közösek). A fenti összefüggéssel megadott függvénykapcsolat egy olyan két rejtett rétegű neuronháló leképezésének is megfeleltethető, ahol a ${\psi }_{pq}\left(x_p\right)$ kapcsolatok adják meg az első rejtett rétegbeli neuronok leképzéseit, az

$y_q\text{=}{\varphi }_q\left({\displaystyle \sum _{p=1}^N{\psi }_{pq}\text{(}{x}_p\text{)}}\right)$ (1.13)

változók pedig a második rejtett réteg kimenetei. Ezekre a rejtett rétegbeli változókra hat a kimeneti réteg, mely az $y_q$ függvényértékek összegét határozza meg. A Kolmogorov-féle reprezentációs összefüggés tehát egy speciális, két rejtett rétegű háló struktúrának felel meg. Mindkét rejtett rétegbeli neuronok nemlineáris neuronok ${\psi }_{pq}(.)$ , illetve a ${\varphi }_q(.)$ transzfer függvényekkel, míg a kimeneti réteg egy egyszerű összegző, itt tehát nincs transzfer függvény.

Míg a Kolmogorov tétel rendkívül ígéretes a neurális háló típusú eszközökkel való approximáció szempontjából, a valós mérnöki feladatok megoldására nem használható közvetlenül. Ugyanis a tétel bizonyítása nem konstruktív, tehát adott N és f esetén sem a ${\psi }_{pq}$ függvényrendszer, sem a ${\varphi }_q$ függvényrendszer előállítására nem ad módszert.

A Kolmogorov tételt az elmúlt évtizedek során többen továbbfejlesztették. Ilyen pl. a David Sprecher által adott finomított tétel. A továbblépés abban áll, hogy a Kolmogorov tételben használt függvényrendszerek helyett csupán két nemlineáris függvény segítségével állítja elő az ismeretlen leképezést. A két függvényt többször is fel kell használjuk a pontos előállításhoz.

1.2 tétel [Spr65]

Létezik olyan monoton növekvő, valós ψ(x): [0,1]→[0,1] függvény, mely csak N-től ( $N\ge 2$ ) függ, és található hozzá ε > 0 úgy, hogy minden folytonos, valós $f\left(x\right):{\left[\mathrm{0,}\text{1}\right]}^N\to ℝ$ függvény felírható az alábbi formában:

$f\text{(}x\text{)=}{\displaystyle \sum _{q\text{=1}}^{2N+1}{\varphi }_q}\left({\displaystyle \sum _{p=1}^N{\lambda }_p{}^{}\psi \left(x_p\text{+}q\epsilon \right)}\right)$ , (1.14)

ahol a ${\varphi }_q$ függvények valós, folytonos függvények, míg a ${\lambda }_p$ értékek alkalmas konstansok.

A Sprecher által kimondott tétel egy olyan – szintén két rejtett réteget tartalmazó – neurális hálózat irányába mutat, amelyben az első rejtett réteg neuronjainak aktivációs függvénye ψ (tehát ez már semmilyen formában nem függ a reprezentálandó függvénytől), míg a második réteg neuronjainál a ${\varphi }_q$ aktivációs függvényeket használjuk. A fenti eredményekre alapozva ki is mondták a 3. fejezetben részletesen tárgyalásra kerülő többrétegű perceptron hálókra vonatkozó tételt.

1.3 tétel [Hec87]

Minden $f\left(x\right):{\left[\mathrm{0,}\text{1}\right]}^N\to ℝ$ négyzetesen integrálható $\left(f\in L_2\right)$ függvény átlagos négyzetes értelemben tetszőleges pontossággal közelíthető legfeljebb két feldolgozó réteget, és a neuronokban szigmoid jellegűnemlinearitást alkalmazó neurális hálózat segítségével.

A fenti tétel, melyet Robert Hecht-Nielsen fogalmazott és bizonyított be két feldolgozó réteget alkalmazó hálóra vonatkozik. A következő tétel azonban ezen gyengíteni tudott, hiszen azt állítja, hogy egy aktív réteg is elegendő ahhoz, hogy egy folytonos függvényt tetszőleges pontossággal közelíteni tudjunk.

1.4 tétel [Fun89]

Legyen g(x) nemkonstans, korlátos, monotonnövekvő folytonos függvény. Legyen továbbá A egy kompakt (korlátos és zárt) részhalmaza ${ℝ}^N$ -nek, és legyen $f\text{(}{x}_1,\dots ,x_N\text{)}$ egy valós értékű folytonos függvény A-n. Ekkor tetszőleges $\epsilon >0$ esetére létezik egy olyan M egész szám, és léteznek $c_{i}i=\mathrm{1,...,}M$ , valamint $w_{ij}$ , i=1, …, M, j=1, …, N konstansok, hogy:

$\widehat{f}\text{(}{x}_1\mathrm{,...,}{x}_N\text{)}={\displaystyle \sum _{i=1}^M{c}_{i}g\left({\displaystyle \sum _{j=0}^N{w}_{ij}{x}_j}\right);x_0=1}$ (1.15)

melyre:

$\underset{x\in A}{\text{max}}\left|f\text{(}{x}_1\mathrm{,...,}{x}_N\text{)}-\widehat{f}\text{(}{x}_1\mathrm{,...,}{x}_N\text{)}\right|<\epsilon$ . (1.16)

Vegyük észre, hogy a Tatsushi Funahashi által megfogalmazott 1.4 tétel nemcsak azt állítja, hogy az (1.16) összefüggés értelmében vett approximációs képességhez egy rejtett réteg elegendő, hanem azt is, hogy ezt a képességet lineáris kimeneti réteggel biztosíthatjuk.

Különösen fontosnak tűnik az utóbbi időben az egy nemlineáris réteggel közelítő hálózatok kutatásának egy másik iránya. A nemlinearitás ezekben a közelítésekben nem az eddigiekben tárgyalt folytonos, monoton, telítődő jellegű függvények közül kerül ki, hanem tipikusan nem monoton, esetleg nem is folytonos függvényeket alkalmazunk. Érdekes, hogy szükséges és elégséges feltételt tudtak kimondani az alkalmazott nemlinearitásra, az alábbi tétel szerint.

1.5 tétel [Les93]

Tetszőleges folytonos $f:ℝ\to ℝ$ függvényt akkor és csak akkor tudunk tetszőleges pontossággal közelíteni lokálisan korlátos aktivációs függvénytalkalmazó neuronokból felépített, egy nemlineáris réteget tartalmazó neurális hálóval, ha az alkalmazott aktivációs függvény nem polinom.

Az 1.5 tétel az aktivációs függvény folytonosságát sem tételezi fel, csupán annyi megkötést tesz, hogy a szakadási helyek nullmértékű halmazt kell alkossanak.

A Funahashi által a perceptron típusú hálózatokra megfogalmazott tétel igen fontos. Hasonló eredményt mások is megfogalmaztak (többek között George Cybenko, [Cyb89], Sean Carroll és Bradley Dickinson [Car89], Takahashi [Tak93]). E tételek részben abban térnek el egymástól, hogy az approximációt milyen értelemben fogalmazzák meg, részben a bizonyítás matematikai részletei mások.

Az eddigiekben olyan approximációs tételeket ismertettünk, melyek valós számok közötti leképezést megvalósító hálókra vonatkoztak, tehát ahol a háló $f:ℝ\to ℝ$ vagy $f:{ℝ}^N\to ℝ$ típusú leképezést valósít meg. A feladatok egy részében (ezek az osztályozási feladatok) azonban a kimenet véges számú lehetséges diszkrét érték közül vehet csak fel értéket.

Cybenko eredménye [Cyb89] kiterjeszthető osztályozós típusú leképezésekre is. Ekkor a háló által megvalósított leképezés: $f:A\subset {ℝ}^N\to \left\{\mathrm{1,2,}\dots ,k\right\}$ , és

$f\text{(}x\text{)}=j$ akkor és csak akkor, ha $x\in A_j$ , (1.17)

ahol A_j, j=1,2,…,k az A tartomány diszjunkt részhalmazait jelöli, vagyis $A=\underset{j=1}{\overset{k}{\cup }}{A}_j$ és $A_i\cap A_j=0$ ,

ha i≠j. Ez az eredmény azt mondja ki, hogy egy egy rejtett réteggel és szigmoid típusú nemlinearitással dolgozó háló nemcsak univerzális approximátor, hanem univerzális osztályozó is. Ezt az eredményt számos kétosztályos osztályozási feladat megoldásával kísérletileg igazolta William Huang és Richard Lippman [Hua88].

Végezetül a neurális hálózatok egyik, egyre jobban terjedő változatára mutatunk approximációs tételt. A 3. fejezetben részletesen tárgyaljuk az RBF (radial basis function) hálózatokat. Ezek tipikusan egy nemlineáris rejtett réteget tartalmaznak, a neuronok aktivációs függvényénekjellegzetessége pedig az N-elemű bemeneti vektorok terében mutatott körszimmetria, melyre neve is utal. (radial = sugaras, ui. a neuronra jellemző középpont paramétertől azonos távolságra − egy r sugarú hipergömbön − elhelyezkedő bemeneti vektorok között nem tesz különbséget a neuron.)

1.6 tétel [Par91]

Legyen az $\psi :{ℝ}^N\to ℝ$ aktivációs függvény a $\left(-\infty ,\infty \right)$ -ben integrálható, folytonos és nem azonosan nulla függvény, mely körszimmetriát mutat az N-elemű bemeneti vektorok halmazán, az euklideszi távolságra nézve. Ekkor bármely $f\in C^N$ függvény tetszőleges pontossággal közelíthető

$f\text{(}x\text{) = }{\displaystyle \sum _{i\text{=}1}^M{w}_i\psi \left(\frac{\Vert x\text{-}{c}_i\Vert }{{\sigma }_i}\right)}$ (1.18)

alakban, ahol $c_i\in {ℝ}^N$ , σ_i és w_i i=1, 2, ..., M a hálózatra jellemző valós paraméterek.

A fentiekben tárgyalt, alapvetően approximációelméleti eredmények olyan modellek irányába mutatnak, melyek struktúrája az 1.2.3 alfejezetben felvázolt előrecsatolt neurális háló. Az eredmények egyik része az 1.3 ábrán látható rendkívül elterjedten használt telítődő jellegű aktivációs függvények használatát sugallja, míg másik része az 1.4 ábrán látható bázisfüggvények használatának irányába mutat.

Az utóbbi években jelentős matematikai kutatások kezdődtek, melyek a fenti eredmények gyakorlati alkalmazhatóságára irányulnak. A kutatások egyrészt az adott pontosságú közelítéshez szükséges neuronszám meghatározását, vagy legalább egy felső korlát felállítását célozzák. Ezek az eredmények azonban már általában nemcsak egy általános neuronháló architektúrát tételeznek fel, hanem kapcsolatot keresnek a háló approximációs hibája, a háló mérete, a tanítópontok száma és a megoldandó probléma bonyolultsága között is; tehát már azzal a kérdéssel is foglalkoznak, hogy adott képességű háló hogyan konstruálható, és azzal is, hogy mennyiben hat a háló képességeire az, hogy véges számú tanítópont felhasználásával konstruáljuk a hálókat. Ezek a kérdések az eddig tárgyaltakhoz hasonló fontosságúak. A legfontosabb eredményeket a következő, a tanulással foglalkozó fejezetben foglaljuk össze, illetve néhány eredményt az egyes háló architektúrákat tárgyaló 3. fejezetben mutatunk be.

Feladatok

1.1 Rajzoljon fel egy FIR/IIR neuront (ld. 1.6 ábra) részletesen felrajzolva a dinamikus hálózatokat! A neuron nemlineáris függvénye legyen egyváltozós (M=1), a bemenetek száma legyen N=2. A neuron mindegyik bemenetén egy-egy két tároló elemet tartalmazó FIR szűrővel, kimenetén pedig egy mind előrevezető, mind visszacsatoló ágában három-három tároló elemet tartalmazó általános IIR szűrővel rendelkezzen! Hány időegységgel késleltetve jelennek meg a bemeneti változások a kimeneten?

1.2 Rajzoljon fel egy FIR/IIR neuront (ld. 1.6 ábra), részletesen felrajzolva a dinamikus hálózatokat. A neuron nemlineáris függvénye legyen egyváltozós (M=1), a bemenetek száma legyen N=2. Mutassa meg, hogy a bemeneteken megvalósított FIR szűrő hogyan transzformálható át az összegző kimenetére!

1.3 Az alábbi aktivációs függvényeket használó neuronok közül, mely(ek) segítségével lehet univerzális approximációs hálózatot építeni (ld. 1.4 − 1.6 tételek)?

_{$g_1\text{(}x\text{)}=\frac{1}{1+x^2}$} ; $g_2\text{(}x\text{)}=x^2$ ; $g_3\text{(}x\text{)}=\text{sin(}x\text{)}\text{, }\left(\text{-}\pi \text{/2}\le x\le \pi \text{/2}\right)$ ; $g_4\text{(}x\text{)}=\frac{1}{\left|x\right|}$ , $g_5\text{(}x\text{)}=x^{T}x$ ; $g_6\text{(}x\text{) = exp}-\left(\frac{{\Vert x-c_i\Vert }^2}{{\sigma }_i}\right)$ .