A neurális hálózatok egyik fontos alkalmazási területe az adattömörítés. Az adattömörítést általában az adatok hatékonyabb reprezentációja céljából végezzük, de alkalmazásával az is lehet a célunk, hogy az eredeti adatokból a későbbi feldolgozás szempontjából lényeges információt kiemeljük, és a lényegtelent elhagyjuk. Az adattömörítést ekkor lényegkiemelés érdekében végezzük. Az adattömörítés − többek között − elvégezhető olyan − lineáris vagy nemlineáris − transzformációk segítségével, amelyek egy adott, többdimenziós térbeli vektort kisebb dimenziós altérbe transzformálnak (vetítenek). Az ilyen típusú feladatoknál két nehézséggel találjuk magunkat szemben. Először is meg kell találnunk azt a kisebb dimenziós alteret, amelyben az eredeti vektor hatékonyan ábrázolható. Másodszor, ha a megfelelő alteret megtaláltuk el kell végezzük a bemeneti vektorok transzformációját.
A hatékony ábrázolás az alkalmazási körtől függően különbözőképpen definiálható. Adattömörítésnél törekedhetünk arra, hogy az altérbe való vetítés során a vektor reprezentációnál a közelítő ábrázolásból adódó hiba minél kisebb legyen. Ebben a megközelítésben definiálni kell valamilyen hibakritériumot, pl. átlagos négyzetes hibát, majd egy olyan, az eredeti dimenziószámnál kisebb dimenziós altér megtalálása a feladat, amelybe vetítve a kiinduló vektort a kritérium szerint értelmezett reprezentációs hiba a lehető legkisebb lesz. Más feladatnál, pl. felismerési vagy osztályozási feladatot megelőző lényegkiemelésnél a reprezentáció akkor tekinthető hatékonynak, ha az altér dimenziója minél kisebb, miközben a közelítő reprezentációban mindazon információ megmarad, amely a felismeréshez, osztályozáshoz elegendő. Ebben az esetben tehát nem követelmény a kiinduló vektor minél kisebb hibájú reprezentálása, csupán arra van szükség, hogy olyan kisebb dimenziós ábrázolást kapjunk, amely a feladat szempontjából szükséges lényeges információkat megtartja.
E feladatok megoldására univerzális eljárás nem létezik. Általában a megfelelő altér feladat- és adatfüggő, tehát a tényleges feladattól függetlenül előre nem meghatározható, és mind az altér meghatározása, mind a transzformáció elvégzése meglehetősen számításigényes. Éppen ezért jelentős eredmény, hogy mind az ellenőrzött, mind a nemellenőrzött tanítású hálózatok körében találunk olyan hálókat, melyek hatékony eszköznek bizonyultak az adattömörítési feladatok megoldására.
A lineáris adattömörítő eljárások között kitüntetett szerepe van a Karhunen-Loève (KL) transzformációnak (KLT), amely az eredeti jeltér olyan ortogonális bázisrendszerét és az eredeti vektorok ezen bázisrendszer szerinti transzformáltját határozza meg, amelyben az egyes bázisvektorok (bázisfüggvények) fontossága különböző. Egy N-dimenziós térből kiindulva az új bázisvektorok közül kiválasztható a legfontosabb M < N bázisvektor, amelyek egy M-dimenziós alteret határoznak meg. Egy vektornak ezen altérbe eső vetülete az eredeti vektorok közelítő reprezentációját jelenti, ahol a közelítés hibája átlagos négyzetes értelemben a legkisebb, vagyis a KLT a közelítő reprezentáció szempontjából a lineáris transzformációk között optimális bázisrendszert határoz meg.
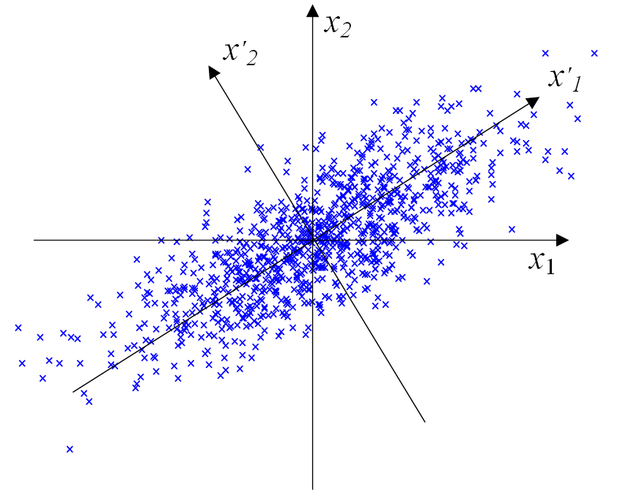
A KL transzformáció működését illusztrálja a 10.5 ábra. A transzformáció feladata az eredeti x1, x2 koordinátarendszerben ábrázolt adatokból kiindulva az x'1, x'2 koordinátarendszer megtalálása, majd az adatoknak ebben az új koordinátarendszerben való megadása. Látható, hogy míg az eredeti koordinátarendszerben a két komponens fontossága hasonló, addig az új koordinátarendszerben a két komponens szerepe jelentősen eltér: x'1 mentén jóval nagyobb tartományban szóródnak a mintapontok, mint x'2 mentén, tehát az egyes mintapontok közötti különbséget az x'1 koordináták jobban tükrözik. Amennyiben az adatok egydimenziós, közelítő reprezentációját kívánjuk előállítani célszerűen x'1-t kell meghagynunk és x'2-t eldobnunk; így lesz a közelítés hibája minimális. A KL transzformáció szokásos elnevezése a matematikai statisztikában faktoranalízis vagy főkomponens analízis (principal component analysis, PCA) . Egy x vektor x'1 és x'2 irányú vetületeit főkomponenseknek is szokás nevezni. Közelítő reprezentációnál a főkomponensek közül csak a legfontosabbakat tartjuk meg, a többit eldobjuk. Az ábrán látható esetben ez azt jelenti, hogy egy x vektor legfontosabb főkomponense az x'1 tengely irányú vetülete.
Az alábbiakban előbb bemutatjuk a KLT származtatását, majd olyan neurális hálózatok felépítésével, működésével és tanításával foglalkozunk, melyek a KLT megvalósítására alkalmasak.
10.3.1. A KL transzformáció és optimalitása
A KL transzformáció alapfeladata a következő: keressük meg azt az ortogonális (ortonormált) bázisrendszert, amely átlagos négyzetes értelemben optimális reprezentációt ad, majd e bázisrendszer segítségével végezzük el a transzformációt. Az eddigiekhez hasonlóan diszkrét reprezentációval dolgozunk, tehát a bemeneti jelet az x N-dimenziós vektorok képviselik, a transzformációt pedig egy T mátrixszal adhatjuk meg.
E szerint a transzformált jel (y) előállítása:
, (10.19)
ahol transzformációs mátrix a
bázisvektorokból épül fel:
. (10.20)
Mivel bázisrendszerünk ortonormált, ezért:
, ebből adódóan
. (10.21)
Feladatunk legyen a következő: x közelítő reprezentációját (
) akarjuk előállítani úgy, hogy a közelítés átlagos négyzetes hibája minimális legyen. Mivel x előállítható, mint a
bázisvektorok lineáris kombinációja
(10.22)
ahol
a
irányú komponens nagysága, és mivel a közelítő reprezentáció
, (10.23)
az átlagos négyzetes hiba felírható az alábbi formában:
. (10.24)
Továbbá, mivel
(10.25)
a következő összefüggés is az átlagos négyzetes hibát adja meg:
, (10.26)
ahol
az x bemenet autokorrelációs mátrixa. A továbbiakban feltételezzük, hogy E{x}=0, ekkor
helyett
, vagyis x kovarianciamátrixa szerepel az átlagos négyzetes hiba kifejezésében.
Ezekután keressük meg azt a
bázist, amely mellett
minimális lesz. Mivel a
feltételt be kell tartanunk, feltételes szélsőértéket kell keresnünk. A Lagrange multiplikátoros módszert alkalmazva
, (10.27)
ahol
-k, (i=M+1,..., N) a Lagrange multiplikátorok. A (10.27) összefüggés
szerinti szélsőértékét keressük, vagyis a
(10.28)
feltételt kell kielégítenünk. Ehhez az szükséges, hogy teljesüljön a
, (10.29)
összefüggés, vagyis a KLT bázisrendszerét alkotó
vektorok a bemeneti jel autokorrelációs (autokovariancia) mátrixának sajátvektorai legyenek. A közelítő, M-dimenziós reprezentáció esetén elkövetett hiba ilyenkor
(10.30)
ahol a
értékek az autokovariancia mátrix sajátértékei.
Minimális hibát nyilvánvalóan akkor fogunk elkövetni, ha a (10.30) összefüggésben a
sajátértékek (i=M+1,...,N) a mátrix legkisebb sajátértékei, vagyis a közelítő, M-dimenziós reprezentációnál az autkovariancia mátrix első M legnagyobb sajátértékéhez tartozó sajátvektort, mint M-dimenziós bázist használjuk fel. A bemeneti jel ezen vektorok irányába eső vetületei lesznek a főkomponensek (innen ered a főkomponenst analízis elnevezés). Megjegyezzük, hogy a KL transzformáció korrelálatlan komponenseket eredményez, vagyis a transzformált jel autokovariancia mátrixa diagonál mátrix, melynek főátlójában a
sajátértékek vannak.
A KLT tehát egy kétlépéses eljárás: először a bemeneti jel autokorrelációs (autokovariancia) mátrixát, és ennek sajátvektorait és sajátértékeit kell meghatározni, majd ki kell választani a legnagyobb M sajátértéknek megfelelő sajátvektort, amelyek a megfelelő altér bázisait képezik. A bázisrendszer ismeretében lehet elvégezni második lépésként a jel transzformációját. Minthogy ez az eljárás meglehetősen összetett (mind a sajátértékek és sajátvektorok meghatározása, mind a későbbi transzformáció elvégzése számításigényes feladat), fontos eredmény, hogy léteznek olyan neurális hálózatok, amelyek e feladatok megoldására alkalmasak. A KLT-t megvalósító neurális hálózatokat az irodalomban PCA hálózatoknak nevezik. E hálózatok a következőkben bemutatásra kerülő Oja szabályon alapulnak.
10.3.2. Az Oja szabály, a legnagyobb sajátértéknek megfelelő sajátvektor meghatározása
A bementi jel legfontosabb főkomponensének (az autokovariancia mátrix legnagyobb sajátértékéhez tartozó sajátvektor irányába eső jel-vetületnek) meghatározására Erkki Oja javasolt egy, a Hebb tanulásonalapuló hálót [Oja82].
A háló egy egyszerű, lineáris, előrecsatolt hálózat, amely legegyszerűbb formájában tulajdonképpen egyetlen, lineáris kombinációt megvalósító processzáló elem. Az Oja háló felépítésében tehát megegyezik a 10.1 ábrán bemutatott egyszerű lineáris neuronnal. Az Oja háló a bemeneti N-dimenziós vektort vetíti a kimeneti egydimenziós térbe. E háló specialitását nem is a felépítése, hanem a tanulási eljárás adja. A súlyok meghatározására a Hebb tanulást, ill. annak módosított változatát alkalmazzuk.
Vizsgáljuk meg, hogy mit eredményez a Hebb tanulás a hálózatnál. Bemenetként N-dimenziós véletlen vektorokat használunk. Megmutatható [Oja82], hogy a hálózat a tanulási szabály alkalmazásával valamilyen egyensúlyi helyzet elérésére törekszik. Ez az egyensúlyi helyzet akkor áll be, ha a súlyvektor a bemeneti vektorok autokorrelációs mátrixának egy sajátvektora lesz. Stabil állapot azonban csak akkor érhető el, ha ez a sajátvektor a legnagyobb sajátértékhez tartozó sajátvektor. Vagyis a hálózat kimenetén a bemenet legfontosabb főkomponensét kapjuk, ami a bementi vektorok legfontosabb sajátvektor irányú vetülete.
A Hebb tanulás önmagában azt eredményezi, hogy a súlyvektorok a tanulás során minden határon túl növekedhetnek. A növekedésnek határt kell szabni, ami normalizálás útján érhető el. A normalizálás biztosítható, ha a Hebb szabályt az alábbiak szerint módosítjuk: legyen a tanulási szabály a következő:
, (10.31)
vagyis egészítsük ki a Hebb tanulási szabályt egy taggal. Az Oja szabály egy olyan w súlyvektorhoz konvergál, amelynek a tulajdonságai az alábbiak:
• a w súlyvektor az R autokorrelációs mátrix legnagyobb sajátértékének megfelelő sajátvektor irányú vektor (a továbbiakban az egyszerűség kedvéért a bemenet autokorrelációs mátrixának jelölésére
helyett R-et használunk).
• a súlyvektor normalizált:
,
• a w irány olyan, hogy a bemenetnek ebbe az irányba eső vetületének lesz a legnagyobb a varianciája, vagyis a kimenet (y) varianciája (
) akkor lesz a legnagyobb, ha y a bemenet w irányú vetületének a hossza. A variancia:
. (10.32)
Egyensúlyi helyzetben
, (10.33)
vagy vektorosan felírva:
. (10.34)
Tehát egyensúlyi helyzetben a súlyvektornak ki kell elégítenie az
(10.35)
összefüggést, ahol
(10.36)
A (10.35) összefüggés mutatja, hogy egyensúlyi állapotban w az R sajátvektora kell legyen, továbbá, ha
=1, akkor λ a megfelelő sajátérték.
Hogy az Oja szabály valóban a Hebb szabály normalizált változata, az alábbiak szerint látható be. Az eredeti Hebb szabály szerint a súlymódosítás:
, (10.37)
ahol most
nem normalizált. Normalizáljuk a módosított súlyvektort:
. (10.38)
meghatározásához írjuk fel
-et, majd ennek (-1/2)-edik hatványát fejtsük Taylor sorba μ=0 környezetében.
(10.39)
Figyelembe véve, hogy
, vagyis hogy az előző lépésben a súlyvektor már normalizált, a következőt kapjuk:
, (10.40)
Felhasználva a (10.37), (10.38) és (10.40) összefüggéseket és a μ-ben magasabbrendű tagokat elhanyagolva:
, (10.41)
ami megfelel (10.31)-nek.
Fentiekben megmutattuk, hogy az Oja szabály alapján végzett tanulás eredményeképp − feltéve, hogy a tanuló eljárás konvergens (a konvergencia tényét azonban nem bizonyítottuk) − a súlyvektor egy λ sajátértékhez tartozó sajátvektorhoz tart. Azt azonban még meg kell mutatni, hogy λ egyben a legnagyobb sajátérték, vagyis
.
Ehhez tételezzük fel, hogy w az R valamelyik sajátvektorához,
-höz áll közel. Vizsgáljuk meg, hogyan alakul a tanulás során a súlyvektor változása, tekintsük a súlyvektorváltozások várható értékét
-t. Minthogy a súlyvektor az egyik sajátvektorhoz áll közel:
és feltéve, hogy normalizált sajátvektorokkal dolgozunk, vagyis
,
, (10.42)
ahol
a
sajátvektorhoz tartozó sajátérték.
Annak eldöntésére, hogy a súlyvektor melyik sajátértékhez tartozó sajátvektorhoz tart, vegyük a súlyvektorváltozás várhatóértékének egy másik normalizált sajátvektorra,
-re vett vetületét és hanyagoljuk el az O(e2) tagot.
(10.43)
Látható, hogy ez a vetület csökken, ha
a nagyobb, és növekszik, ha
a nagyobb sajátérték. Tehát ha
>
, akkor a súlyvektor a nagyobb sajátértéknek megfelelő sajátvektor irányába fordul be.
Az Oja algoritmus, mint szélsőérték-kereső eljárás
Az Oja algoritmus a fentiektől eltérően szélsőérték-kereső eljárás eredményeként is származtatható, minthogy a bemenő sztochasztikus vektorfolyamat mintáinak a legnagyobb sajátvektor irányában vett vetülete várható értékben maximumot kell adjon. Keressük tehát
maximumát w függvényében.
(10.44)
Felírva a deriváltat és figyelembe véve, hogy
adódik, hogy
. (10.45)
Ha figyelembe vesszük, hogy
, (10.46)
továbbá, ha az LMS algoritmushoz hasonlóan a pillanatnyi gradiens alapján számolunk, vagyis a várhatóérték-képzést nem végezzük el, akkor:
, (10.47)
ami az Oja szabályt adja. Az Oja szabály (10.47) összefüggése egy sztochasztikus gradiens algoritmus, mivel a gradiens számításnál a várhatóérték-képzést elhagyjuk.
Megjegyezzük, hogy az (10.44) összefüggést Rayleigh hányadosnak is nevezik [Gol96b], mely, ha w az R mátrix egy sajátvektora, a hányados a megfelelő sajátértéket adja. Ebből is következik, hogy (10.44) w szerinti maximuma a legnagyobb, minimuma a legkisebb sajátértéket eredményezi.
Összefoglalva, megállapítható, hogy az Oja hálózat a módosított Hebb tanulással, a legnagyobb sajátértéknek megfelelő sajátvektort alakítja ki súlyvektorként, amennyiben a tanulási szabály konvergens. A konvergencia bizonyítható, azonban a bizonyítás menete bonyolult és az eljárás lényegének megértéséhez nem járul hozzá, ezért nem mutatjuk be. A bizonyítás a megfelelő irodalomban [Oja82] megtalálható.
10.3.3. Főkomponens- és altér hálózatok
A különböző alkalmazásokban a legfontosabb sajátvektornak és az ebbe az irányba eső főkomponensnek a meghatározása általában nem elegendő. Olyan hálózatot szeretnénk kapni, amely N-dimenziós bemenetből kiindulva az M legfontosabb sajátvektor (M ≤ N) meghatározására képes.
Az Oja hálózatot, illetve az Oja szabályt többféleképpen módosították, melynek eredményeképpen létrejött hálózatok alkalmasak a teljeskörű főkomponens analízisre, vagyis képesek a bemeneti jel KL transzformáltjának meghatározására. Ezeket a hálózatokat főkomponens hálózatoknak (principal component networks) nevezzük.
Az Oja hálózaton alapuló hálózatok egy másik csoportja, amely csoport tagjai − bár nem a tényleges főkomponenseket, vagyis a legfontosabb sajátvektorok irányába eső vetületeket határozzák meg − a főkomponens analízissel rokon eredményre vezetnek. Adattömörítésnél ugyanis nincs feltétlenül szükség magukra a főirányokra, tehát a legfontosabb sajátvektorokra, sokszor elegendő, ha csak azt az alteret és ebbe az altérbe eső vetületet határozzuk meg, amelyet az első M legfontosabb sajátvektor feszít ki. Az alteret nemcsak a sajátvektorok határozzák meg, hanem bármely bázisa. Azokat a hálózatokat, amelyek az alteret és a bemeneti vektorok altérbe eső vetületeit meghatározzák, de a sajátvektorokat nem, altér hálózatoknak (subspace networks) nevezzük. Az alábbiakban előbb egy altér hálózatot ismertetünk, majd az eredeti Oja hálózat olyan módosításait vizsgáljuk, amelyek a tényleges főkomponensek meghatározását eredményező hálózatokra vezetnek.
Az Oja altér hálózat az Oja algoritmussal tanított elemi neuron kiterjesztése olyan többkimenetű hálózattá, amely nem a legfontosabb főkomponens meghatározását végzi, hanem az első M sajátvektor által kifeszített altérbe vetít. A hálózat tehát átlagos négyzetes értelemben minimális hibájú közelítést eredményez. Minimális átlagos négyzetes eltérést biztosító megoldást kapunk, ha az eredeti Oja szabályt egy M-dimenziós y kimeneti vektorra alkalmazzuk. Az eredmény az Oja általánosított szabály [Oja83]:
, (10.48)
ahol
az M-kimenetű háló súlyvektoraiból, mint sorvektorokból képezett mátrix.
Az Oja altér hálózat egy N-bemenetű−M-kimenetű hálózat, amely egyetlen, lineáris neuronokbólfelépülő rétegből áll. Mivel az Oja altér háló súlyvektorai nem a sajátvektorokhoz konvergálnak, hanem a sajátvektorok által kifeszített tér egy bázisához, az általánosított Oja szabályt Oja altér szabálynak is szokás nevezni.
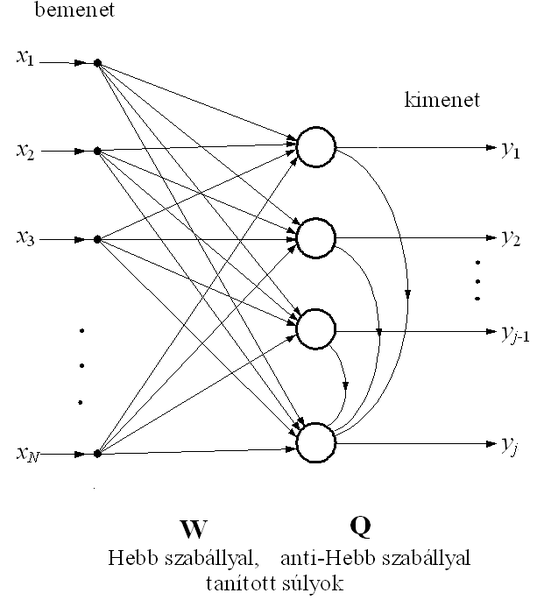
Az Oja altér hálózaton kívül egyéb, kisebb-nagyobb mértékben eltérő felépítésű altér hálózatot publikáltak (pl. [Föl89]). A Földiák háló az előrecsatoló súlyokon kívül a neuronok között szimmetrikus oldalirányú súlyozott kapcsolatokat is használ. Az előrecsatoló súlyokat a Hebb szabállyal, az oldalirányú kapcsolatok súlyait pedig az anti-Hebb szabállyal tanítja. Bizonyítható, hogy az előrecsatoló súlyvektorok itt is olyan vektorokhoz konvergálnak, melyek a megfelelő számú legfontosabb sajátvektor által kifeszített tér egy bázisát képezik. Ez, illetve egyéb altér háló változatok lényegi újdonságot – különösen a műszaki alkalmazási lehetőségeket tekintve – nem hoznak, ezért a részletesebb bemutatásukra nem térünk ki.
Az alábbiakban a valódi főkomponensek meghatározására alkalmas két hálózatot mutatunk be. E hálózatok a processzáló elemek számának megfelelő számú sajátvektort és a bemeneti vektorok ezen sajátvektor irányokba eső vetületeit határozzák meg olyan módon, hogy M processzáló elem esetén az első M legnagyobb sajátértéknek megfelelő sajátvektort és a hozzájuk tartozó vetületeket szolgáltatják. A két eljárás – bár kissé eltérő architektúrával rendelkeznek és a tanulási szabályaik sem azonosak – hasonló elveken alapul: mindkettő az eredeti Oja szabályt kombinálja a Gram-Schmidt ortogonalizálási eljárással.
A Sanger algoritmus (Generalized Hebbian Algorithm, GHA)
A Sanger hálózat egy N-bemenetű, M ≤ N kimenetű lineáris előrecsatolt hálózat, amelynek első kimenete a legfontosabb főkomponenst az Oja szabály szerint határozza meg. Az első neuronnak a súlyvektora a legnagyobb sajátértékhez tartozó sajátvektor. A további neuronok szintén az Oja szabályt alkalmazzák, azonban az eredeti bemenőjeltől eltérő bemenetekre. Az eltérő bemeneteket Gram-Schmidt ortogonalizálással állítjuk elő. Az eredeti bemenőjelből kivonjuk a már előállított főkomponenseket és az így kapott jelre alkalmazzuk az Oja szabályt.
Nyilvánvaló, hogy ha a bemenőjelből kivonjuk az első főkomponenst, a módosított bemenőjel legfontosabb főkomponense (és a módosított bemenőjelhez rendelt autokorrelációs mátrix első sajátvektora) az eredeti jel második legfontosabb főkomponese (az eredeti autokorrelációs mátrix második sajátvektor irányára vetített komponens) lesz. A hálózat második neuronja ezért a második legfontosabb sajátvektort és az ebbe az irányba eső jelkomponenst állítja elő. A hálózatot további processzáló elemekkel bővítve és az eljárást tovább folytatva az összes sajátvektor, illetve főkomponens meghatározható.
Az eljárás bemutatásához vezessük be az alábbi jelölést: legyen
az i-edik neuronra kerülő módosított bemenet. Ez azt jelenti, hogy
a hálózat eredeti bemenőjele.
Az Oja szabály szerint az első neuron súlyvektorának tanító összefüggése:
. (10.49)
Képezzük a módosított bemenetet, vagyis vonjuk ki az eredeti bemenetből a bemenetnek az első sajátvektorra eső komponensét:
, (10.50)
és erre alkalmazzuk ismét az Oja szabályt:
(10.51)
A módosított bemenet előállításánál figyelembe vettük, hogy a súlyvektor normalizált, vagyis
Hasonlóan tovább folytatva az eljárást és figyelembe véve, hogy a további súlyvektorok hossza is egységnyi, az i-edik súlyvektor módosító összefüggésére a következőt kapjuk:
(10.52)
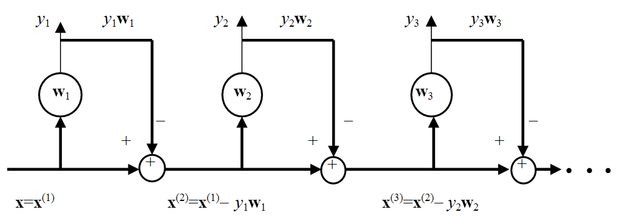
A 10.6 ábra azt mutatja, hogy hogyan számítjuk ki az egymást követő főkomponenseket. A háló összes súlyvektorának módosító összefüggését egy közös egyenletbe is összefoghatjuk. A fenti algoritmust vektorosan felírva kapjuk a Sanger tanulási szabályt, amit általánosított Hebb algoritmusnak(Generalized Hebbian Algorithm, GHA) is szoktak nevezni [San89]:
, (10.53)
ahol W hasonlóan az Oja altér háló összefüggéséhez most is a háló súlyvektoraiból, mint sorvektorokból képezett mátrix.
A Sanger szabály (10.53) szerinti összefüggése nagyon hasonló az általánosított Oja szabály (10.48) összefüggéséhez. A különbség mindössze annyi, hogy a zárójelen belüli kifejezés második tagját képező mátrixnak a Sanger szabálynál csak az alsó háromszög mátrixával (LT) dolgozunk. Ez valójában azt fejezi ki, hogy itt egy hierarchikus számítási modellről van szó.
Az APEX háló szintén a főkomponensek meghatározására alkalmas. Felépítése hasonló az Oja altér háló felépítéséhez azzal kiegészítve, hogy itt a neuronok között egyirányú laterális kapcsolatok is vannak. Valójában ez a háló is az Oja szabály és a Gram-Schmidt eljárás kombinálásával dolgozik, azonban ezt módosított architektúrával, oldalirányú kapcsolatok bevezetésével éri el. A hálózat a főkomponenseket egyenként, egymás után határozza meg, és oldalirányú kapcsolatok csak a már meghatározott kimenetek és az éppen meghatározás alatt álló kimenet között vannak (10.7 ábra).
A hálózat tanításának összefüggéseit arra az esetre adjuk meg, amikor feltételezzük, hogy az első j−1 processzáló elem súlyai már beálltak, és most a j-edik neuron tanítása folyik. A hálózat j-edik kimenete:
, (10.54)
ahol
a hálózat első j−1 kimenetéből képezett vektor,
a j-edik kimenet előrecsatoló súlyvektora,
pedig az első j−1 kimenetről a j-edik kimenethez csatoló oldalirányú kapcsolatok súlyvektora.
A súlymódosítás összefüggései a j-edik processzáló elem számára az alábbiak:
, (10.55)
és
. (10.56)
Látható, hogy az előrecsatoló súlyok tanítása az Oja szabállyal, a laterális kapcsolatok tanítása a módosított anti-Hebb szabállyal (tulajdonképpen az anti-Oja szabállyal) történik. Bizonyítható [Dia96], hogy konvergencia esetén az előrecsatoló súlyvektor a j-edik legnagyobb sajátértékhez tartozó sajátvektorhoz, az oldalirányú csatolás súlyvektora pedig 0-hoz tart. Megmutatható az is [San93], hogy a GHA és az APEX megoldás lényegében ekvivalensek. Mindkettő valójában egymás után, egyenként, csökkenő „fontossági” sorrendben (csökkenő sajátértékek szerint) határozza meg a sajátvektorokat és a bemeneti jel főkomponenseit. Egyik háló sem állítja elő ugyanakkor a megfelelő sajátértékeket, bár ezek a kimeneti értékek átlagos négyzetes értékeivel becsülhetők. Ugyancsak közös mindkét hálónál, hogy legpontosabban a legfontosabb sajátvektort határozzák meg, az egyre csökkenő fontosságúak hibái − minthogy meghatározásukban szerepet játszanak a rangsorban előttük állók − egyre növekednek.
Fontos kérdés még a hálózatok megfelelő működéséhez a
tanulási tényező megválasztása. Egyrészt magát a konvergenciát is befolyásolja, hogy milyen tanulási tényezőt választunk, másrészt, ha konvergens is az eljárás, a konvergenciasebesség is nagymértékben függ
értékétől. A PCA hálózatok konvergenciájának bizonyítása a sztochasztikus approximáció eredményein alapul, ezért itt is bizonyos számú tanító lépésenként csökkenő
alkalmazása (ld. (2.136) összefüggés) célszerű, bár nagyon sok alkalmazásban konstans
felhasználását javasolják. Ez utóbbi esetben a konvergenciát úgy biztosíthatjuk, ha megfelelően kicsire választjuk
-t. Az APEX hálónál az is megmutatható, hogy létezik optimális, lépésenként változó tanulási tényező is, amely ráadásul neuronfüggő. A j-edik PE súlyainak tanításához a k-adik lépésben az optimális tanulási faktor:
, (10.57)
ahol
a hálózat j-edik kimenetének átlagos négyzetes értéke (varianciája). Az optimális érték helyett a gyakorlatban könnyebben alkalmazható az alábbi összefüggés szerint választott együttható [Kun90]:
, (10.58)
Ezzel a választással a biztonságos, de kissé lassúbb konvergencia irányában módosítjuk
-t, hiszen
a j-edik sajátérték,
becslése (
→
ha k→∞), és
<
.
A PCA hálózatok egyik legfőbb előnye az egyéb KLT eljárásokhoz képest, hogy a transzformációt nem két, hanem egyetlen lépésben végzik. Nincs szükség tehát előbb a bemeneti jel autokorrelációs (autokovariancia) mátrixának meghatározására és ennek alapján a sajátvektorok kiszámítására, hanem közvetlenül a bemeneti adatokból dolgozhatunk. Ennek ellenére nem állíthatjuk, hogy a neurális módszer a legjobb a KLT meghatározására. Számos olyan kérdés merül föl (konvergenciasebesség, pontosság, beleértve a numerikus pontosságot is), melyek részletes elemzése még nem vagy csak részben történt meg.
A PCA hálózatok aszimptotikusan a KL transzformációt eredményezik, így az optimális lineáris transzformáció megvalósításának eszközei. Számos gyakorlati feladatnál szokás azonban egyéb transzformációkat alkalmazni, melyek az optimális transzformációt csak közelítik, de melyek kiszámítása lényegesen egyszerűbb (pl. képtömörítésnél a KL transzformáció helyett a diszkrét koszinusz transzformációt (DCT) alkalmazzák [Wal91]).
Az eddigi adattömörítő hálózatokra jellemző, hogy lineáris egyrétegű felépítéssel rendelkeznek. A következőkben röviden bemutatjuk, hogy adattömörítést többrétegű hálózatokkal is lehetséges.
10.3.4. Lineáris többrétegű perceptron, mint adattömörítő hálózat
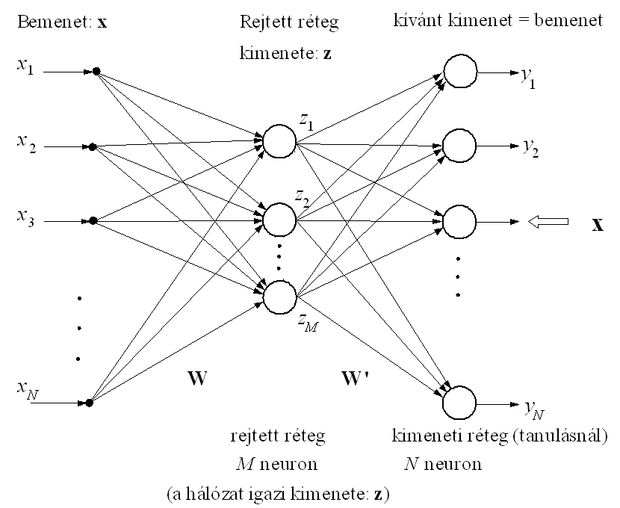
Képzeljünk el egy olyan két aktív rétegű perceptront, amely lineáris neuronokbólépül fel és autoasszociatív módon működik, vagyis adott bemenetre válaszként magát a bemenetet várjuk. Az autoasszociatív hálóknál a kívánt kimenet megegyezik a bemenettel. Amennyiben a rejtett rétegbeli neuronok száma (M) kisebb, mint a bemenetek (és ennek megfelelően a kimenetek) száma (N), akkor a rejtett rétegbeli neuronok kimenő értékei a bemenet tömörített (közelítő) reprezentációját adják (ld. 10.8 ábra).
A rejtett réteg képezi a háló "szűk keresztmetszetét". Ha a hálót a szokásos hibavisszaterjesztéses algoritmussal tanítjuk, a háló által előállított kimenet (y) átlagos négyzetes értelemben közelíti a háló bemeneti jelét (x). A háló kimeneti rétege a rejtett rétegbeli M-dimenziós reprezentációból állítja vissza az N-dimenziós kimenetet, tehát a rejtett réteg kimenetén a bemenőjel kisebb dimenziós altérbe vett vetületét kapjuk meg, olyan módon, hogy e közelítő ábrázolásból az eredeti jel a legkisebb átlagos négyzetes hibával állítható vissza. Az altér lineáris neuronokmellett bizonyítottan [Bal89] a megfelelő KLT alteret jelenti, de az altérben a bázisvektorok nem feltétlenül lesznek a sajátvektorok.
Megmutatható, hogy az autoasszociatív hálózat hibája nem függ attól, hogy a rejtett rétegbeli neuronok lineáris vagy nemlineáris kimenettel rendelkeznek. A háló mindkét esetben a bemenetnek a főkomponensek alterébe eső vetületét adja.
Az adattömörítő többrétegű perceptron olyan hálózatra példa, ahol annak ellenére, hogy lineáris processzáló elemekkel dolgozunk, a több réteg alkalmazásának értelme van, ugyanis épp a közbenső, kisebb dimenziós rejtett réteg szolgáltatja a bemenet tömörített változatát.