Az utóbbi időben több olyan eredmény is született, melyek nemlineáris kiterjesztései a PCA illetve az altér hálóknak. A nemlineáris hálók működésének elve nagymértékben hasonlít az eddig bemutatott PCA hálókéhoz azzal a különbséggel, hogy a nemlineáris hálóknál nem közvetlenül a bemeneti adatokat dolgozzuk fel, hanem előbb egy nemlineáris transzformációt alkalmazunk – amely általában dimenziónövelő transzformáció is egyben –, majd a transzformált adatokra alkalmazzuk a már ismert eljárásokat. A nemlineáris transzformáció miatt itt esetenként a lineáris hálókénál is nagyobb mértékű tömörítés, ill. azonos mértékű tömörítés mellett kisebb hiba is elérhető.
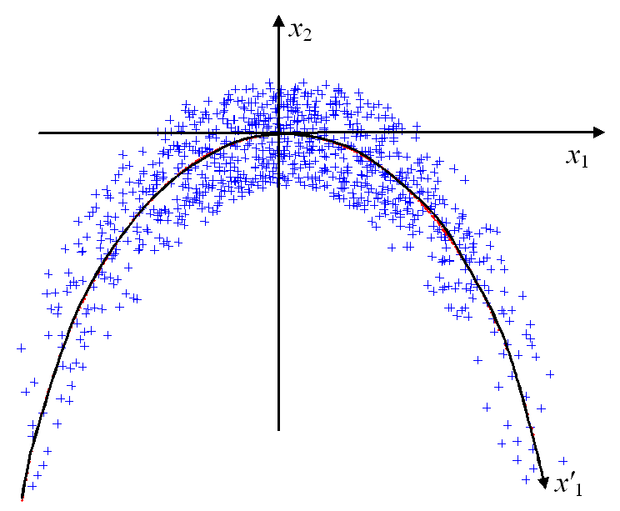
A nemlineáris tömörítésre mutat példát a 10.9 ábra. Az ábrán látható adatok esetén nem találunk olyan lineáris transzformációt, melynek alkalmazását követően a kétdimenziós adatok olyan egydimenziós reprezentációját nyernénk, hogy a közelítés átlagos négyzetes értelemben vett hibája ne lenne jelentős. Nemlineáris transzformációt is megengedve – tehát ha az ábrán az x1, x2 koordinátarendszer helyett az x'1, és az x'1-re minden pontban merőleges x'2 koordinátarendszerben adjuk meg az adatokat – látható, hogy az x'2 koordináta elhagyása átlagos négyzetes értelemben az adatok reprezentációjában csak kis hibát eredményez: az így kapott egydimenziós reprezentáció hibája jóval kisebb, mintha az eredeti komponensek bármelyikét hagytuk volna el.
A főkomponens analízis célja az adattömörítésen kívül más is lehet. Sok esetben nem az adatok dimenzióját akarjuk redukálni, hanem a főkomponensek meghatározásával az adatok belső struktúráját szeretnénk meghatározni. A 10.9 ábrán bemutatott példa esetében sem feltétlenül az a cél, hogy a kétdimenziós reprezentáció helyett egydimenziós közelítő reprezentációt kapjunk. Önmagában annak a felismerése is hasznos lehet, hogy az x'1-menti és egy erre merőleges komponens az adatok struktúráját jobban kifejezi, mintha az eredeti x1 és x2 komponenseket használnánk. A főkomponenseket ezért nemcsak a bemeneti térben, az adatok eredeti reprezentációja mellett, hanem valamilyen nemlineáris transzformáció útján kapott jellemzőtérben is érdemes keresni. A nemlineáris transzformáció közbeiktatása miatt az adatok komponensei között magasabbrendű korreláció, az adatokban rejtve meglévő valamilyen nemlineáris struktúra felderítése is lehetséges.
A nemlineáris főkomponens analízis eljárásoknál is – hasonlóan a lineáris eljárásokhoz – olyan új koordinátarendszert keresünk, melynek egyes koordinátái jelentős mértékben eltérő fontosságúak az adatok előállításában. A kétféle eljárás közötti alapvető különbség, hogy itt a megfelelő transzformáció keresését nem korlátozzuk a lineáris transzformációk körére. A jellemzőtérben történő főkomponens analízis elvégzéséhez előbb meg kell határozni a jellemzőtérre való leképezés nemlineáris transzformációját, majd ebben − a bemeneti térnél sokszor nagyobb dimenziós − térben kell elvégezni a főkomponensek meghatározását. A módszer nehézségét már lineáris eljárásnál is az okozta, hogy a transzformáció bázisa a kiinduló jel függvénye. Nemlineáris esetben a megfelelő transzformáció megtalálása és hatékony megvalósítása még nehezebb feladat.
A következőkben két nemlineáris eljárást mutatunk be. Az első eljárásnál alkalmazott nemlineáris transzformáció általában a bemeneti térnél sokkal nagyobb dimenziós jellemzőteret eredményez, azonban a jellemzőtérbeli főkomponens analízist nem ebben a térben, hanem az ebből származtatott kernel térben tudjuk megoldani. Itt tehát nincs szükség a jellemzőtérbeli transzformáció explicit definiálására és a jellemzőtérbeli reprezentáció meghatározására. A kernel gépeknél bemutatott kernel trükk segítségével ugyanis a jellemzőtérbeli főkomponens analízis elvégezhető a kernel térben is. Az ún. kernel PCAcélja az adatokban meglévő rejtett (nemlineáris) struktúra meghatározása. A kernel PCA tehát elsődlegesen nem adattömörítésre szolgál.
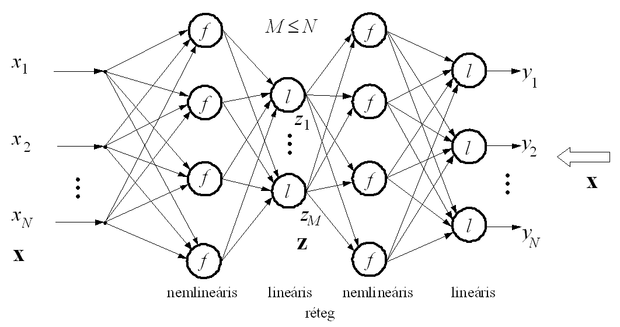
A második bemutatott megoldás nemlineáris adattömörítéstvégez, mégpedig többrétegű perceptronnal. A megoldás tehát az előzőekben bemutatott perceptron-alapú altér háló nemlineáris megfelelője.
A PCA során a bemeneti térben keresünk főkomponenseket úgy, hogy a bemenetek megfelelő lineáris transzformációját végezzük. A kernel PCA ezzel szemben nem a bemeneti térben keres főkomponenseket, hanem előbb a bemeneti vektorokat nemlineáris transzformációval egy ún. jellemzőtérbe transzformálja, és itt keres főkomponenseket.
Az eljárás bemutatásához a következő jelölésekből induljunk ki. Jelöljük a bemeneti térből a jellemzőtérbe való nemlineáris transzformációt Φ-vel. A bemeneti tér lehet pl. a valós szám N-esek tere,
, ekkor a nemlineáris transzformáció
-ből egy F jellemzőtérbe képez le:
(10.59)
Az F jellemzőtér tetszőlegesen sokdimenziós, akár végtelen dimenziós tér is lehet. Tételezzük fel, hogy az F térben is fennáll, hogy
, ahol P a bemeneti vektorok száma. Becsüljük a jellemzőtérbeli kovarianciamátrixot a véges számú mintapont (jellemzőtérbeli vektor) alapján:
(10.60)
A jellemzőtérbeli főkomponensek meghatározásához először most is meg kell határoznunk a kovarianciamátrix nemnulla sajátértékeit és a megfelelő sajátvektorokat, melyek kielégítik a szokásos sajátvektor-sajátérték egyenletet:
, (10.61)
majd a jellemzőtérbeli főkomponenseket a
jellemzőtérbeli vektorok és az egységnyi hosszúságúra normált V sajátvektorok skalár szorzataként kapjuk.
A sajátértékek és a sajátvektorok meghatározásához hasznos, ha felhasználjuk, hogy a
kovarianciamátrix sajátvektorai a jellemzőtérbeli vektorok által kifeszített térben vannak:
, (10.62)
tehát léteznek olyan
(i=1,…,P) együtthatók, melynek segítségével a sajátvektorok előállíthatók a bemeneteket a jellemzőtérben reprezentáló vektorok súlyozott összegeiként. A (10.62) összefüggés felhasználásával azonban meg tudjuk mutatni, hogy a jellemzőtérbeli főkomponensek anélkül is meghatározhatók, hogy a bemeneti vektorok jellemzőtérbeli reprezentációját meghatároznánk.
Ennek érdekében tekintsük a következő egyenletet:
, k=1,…,P (10.63)
Helyettesítsük ebbe az egyenletbe
(10.60) és V (10.62) összefüggését. Ekkor minden k=1,…,P-re a következőt kapjuk:
(10.64)
Vegyük észre, hogy ebben az összefüggésben a jellemzőtérbeli
vektorok mindig csak skalár szorzat formájában szerepelnek.
Definiáljunk egy
méretű K kernel mátrixot, melynek (i,j)-edik eleme:
. (10.65)
Ezzel a (10.64) összefüggés az alábbi tömör formában is felírható:
, (10.66)
ahol az
oszlopvektor az
i=1,…,P együtthatókból áll. K szimmetrikus mátrix, és ha megoldjuk a következő sajátvektor-sajátérték problémát:
, (10.67)
ahol az
vektorok K sajátvektorai és a Pλ értékek a sajátértékek, a megoldás kielégíti a (10.66) egyenletet is. Jelöljük K nemnulla sajátértékeit nagyság szerint sorbarendezve
-vel, a hozzájuk tartozó sajátvektorokat pedig
-vel, és legyen
az első (legkisebb) nemnulla sajátérték. (Ha feltételezzük, hogy
nem azonosan 0, akkor mindig léteznie kell egy ilyen
-nek.) Normalizáljuk az
sajátvektorokat, hogy az F térben a következő egyenlőség teljesüljön k=r,…,P–re :
(10.68)
Ez a következő normalizálási feltételt szabja az
sajátvektorokra:
(10.69)
A főkomponensek meghatározása után szükségünk van még a jellemzőtérbeli vektorok sajátvektorok szerinti vetítésére. Legyen x egy tesztpont,
képpel F-ben, ekkor
(10.70)
A jellemzőtérbeli főkomponens tehát a közvetlenül a kernel értékek függvényében kifejezhető, anélkül, hogy a
nemlineáris leképezéseket meg kéne határozni. Tehát itt is a kernel trükköt alkalmazhatjuk, ha a nemlineáris PCA számítását nem a
nemlineáris leképezések rögzítésével, hanem a K mátrix (a kernel függvény) megválasztásával végezzük. A kernel PCA-nál tehát nem a
nemlineáris leképezésekből, hanem a kernel függvényből indulunk ki. A kernel függvény implicit módon definiálja a jellemzőtérbeli leképezést.
Összefoglalva a következő teendőink vannak a főkomponensek meghatározása során. Először meg kell választanunk a kernel függvényt, majd meg kell határoznunk a K mátrixot. Ennek a mátrixnak kell kiszámítanunk az
sajátvektorait. A sajátvektorok normalizálását követően határozhatjuk meg a bemeneti vektorok jellemzőtérbeli főkomponenseit a (10.70) összefüggés felhasználásával.
Az eljárás fő előnye abban rejlik, hogy a
függvény ismeretére nincs szükségünk, továbbá, hogy míg az eredeti PCA során a kovarianciamátrix mérete a bemeneti dimenziótól függ, addig itt a K mátrix méretét a tanítópontok száma határozza meg. Lineáris PCA-nál legfeljebb N sajátvektort és így N főkomponenst találunk, ahol N a bemeneti vektorok dimenziója. Kernel PCA-nál maximum P nemnulla sajátértéket kaphatunk, ahol P a mintapontok száma.
A nulla várhatóérték biztosítása a jellemzőtérben
A korábbiakban tényéként kezeltük, hogy az F térben igaz a
megállapítás. Ez nyilvánvalóan nem lehet igaz minden
függvényre, így szükségünk van arra, hogy a
jellemzőtérbeli vektorokat is 0 átlagértékűvé transzformáljuk. Ez megoldható, ha a vektorokból kivonjuk az átlagukat:
(10.71)
Az eddigi megállapítások szerint most ez alapján kell meghatározni a kovarianciamátrixot, illetve a
(10.72)
mátrixot az F térben. Az így kapott
mátrix sajátérték-sajátvektor rendszerét kell meghatároznunk:
(10.73)
ahol
a sajátvektorok együtthatóit tartalmazza a következő formában:
. (10.74)
A
mátrix kiszámítása a definíciós összefüggés szerint azonban nem lehetséges a módosított jellemzőtérbeli vektorok ismerete nélkül. Lehetőségünk van viszont arra, hogy a
mátrixot K-val kifejezzük.
Használjuk a következő jelöléseket:
,
minden i, j-re és
. Ezek után
számítása:
(10.75)
Ezután számíthatók ki a sajátértékek és a sajátvektorok, a főkomponensek számítása pedig ugyanaz, mint a nem központosított adatok esetében.
Láttuk, hogy a kernel PCA a jellemzőtérben határoz meg főkomponenseket, ezért a főkomponensekből szintén a jel jellemzőtérbeli reprezentációját tudnánk előállítani. Azt is láttuk ugyanakkor, hogy a kernel trükk miatt valójában nem is dolgozunk a jellemzőtérben, hiszen a jellemzőtérbeli vetületeket is meg tudjuk határozni a kerneltérbeli reprezentáció segítségével. Ha azt szeretnénk tudni, hogy mi a jellemzőtérbeli közelítő reprezentáció hatása a bemeneti térben, akkor a jellemzőtérbeli főkomponensekből vissza kell állítanunk a jelet a bemeneti térben. Ez a feladat egyáltalán nem triviális, sőt nem is feltétlenül egyértelmű. A jelvisszaállításra Sebastian Mika [Mik99] és munkatársai javasoltak közvetett eljárást. E szerint a bemeneti térben keresünk olyan vektort, amelynek jellemzőtérbeli főkomponensei minél inkább hasonlóak a visszaállítandó jel főkomponenseihez.
Jelöljük az eredeti jel m főkomponens alapján kapott jellemzőtérbeli közelítő reprezentációját
-mel. Ekkor
, (10.76)
vagyis a közelítő reprezentáció a jellemzőtérbeli sajátvektorok lineáris kombinációjaként állítható elő. A jelvisszaállításhoz olyan bemenetet keresünk, melynek a jellemzőtérbeli képe minél kisebb mértékben tér el
-től. E mögött az a feltevés áll, hogy ha két jel jellemzőtérbeli reprezentációja között az eltérés kicsi, akkor a bemeneti térben is kicsi a köztük lévő eltérés. Négyzetes hibakritériumot alkalmazva ez azt jelenti, hogy keressük azt az
bemeneti vektort, melyre
(10.77)
minimális. Behelyettesítve (10.77)-be (10.76)-ot és V(k) (10.62) összefüggését, az eltérésre a következőt kapjuk:
(10.78)
ahol Ω függtelen
-től. A (10.78) kritérium minimumát biztosító
gradiens eljárással megkereshető, ha rögzítettük a kernel függvényt.
10.1 példa
A kernel PCA működését egy egyszerű példán illusztráljuk [Sch96c]. Egy kétdimenziós adathalmaz főkomponenseit keressük, ahol az adatok generálása a következő módon történt: egy mintapont x1 komponense a [-1,1] intervallumba egyenletes eloszlású véletlen szám, x2 komponensét pedig az alábbi kapcsolat alapján határozhatjuk meg
ahol ξ egy nulla várható értékű σ=0,2 szórású normális eloszlású véletlen zaj.
Válasszunk a feladat megoldásához polinomiális kernelt:
A 10.10 ábra különböző q értékekre mutatja a főkomponens analízis eredményét. Balról jobbra az egyes oszlopok rendre q=1, 2, 3 és 4 érték melletti polinomiális kernellel született eredményeket mutatnak olyan módon, hogy az egyes oszlopokban a három legnagyobb sajátértéknek megfelelő eredmény látható. Az ábrán a vonalak a konstans főkomponensek kontúr vonalai.
A bal szélső oszlop a q=1 esethez tartozik, ami valójában a lineáris PCA. Látható, hogy itt csak két sajátérték lesz nullától különböző, ami triviális is kétdimenziós bemenetek esetében. Lineáris PCA-nál a sajátvektorok az ábra vonalaira merőleges irányúak és nyilvánvalóan egymásra is merőlegesek. Az első oszlop ábráiból az is látható, hogy az adott példában a lineáris PCA főkomponensei nem tükrözik az adatok struktúráját.
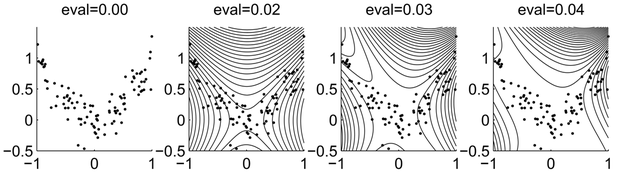
A magasabb fokszámú esetekre a főkomponensek már visszaadnak valamit az adatok struktúrájából. Ez jól látszik a három utolsó oszlop legfelső, a legfontosabb jellemzőtérbeli sajátértékekhez tartozó ábráiból. A magasabb fokszámú esetekben a jellemzőtér dimenziója nagyobb, mint a bemeneti tér dimenziója, így itt a várakozásnak megfelelően kettőnél több nemnulla sajátérték lehet. A második oszlopban (q=2) a harmadik főkomponens − ami a legkisebb sajátértékhez tartozik − az additív Gauss zaj szerepét mutatja.
Ez utóbbi megfigyelés arra is utal, hogy a kisebb sajátértékekhez tartozó főkomponensek sok esetben az adatokat terhelő zajhoz köthetők. Ilyenkor ezeknek a főkomponenseknek az elhagyása elsősorban nem a dimenzióredukciót, hanem a zajszűrést, az adatok „zajtalanítását” (denoising) szolgálja. A PCA eljárások mind lineáris mind nemlineáris esetben eredményezhetnek zajtalanítást. Ezt illusztrálja a következő példa.
10.2 példa
A kernel PCA zajtalanító hatását egy éles feladatra való alkalmazáson mutatjuk be. A feladat kézzel írott számjegyek felismeréséhez kapcsolódik [Mik99]. A kiinduló minták 16×16 pixeles szürkeárnyalatos képek, melyeket különböző tulajdonságú additív zaj terhel. A feladatban a kernel PCA alkalmazása azt illusztrálja, hogy a kernel térben a legfontosabb főkomponensek meghagyása és a kisebb sajátértékekhez tartozó főkomponensek elhagyása alkalmas lehet a képek zajszűrésére. A példa ugyanakkor azt is illusztrálja, hogy az adott feladatban a lineáris PCA a zajszűrést megfelelő minőségben nem tudja megoldani.
A 10.11 ábra mind a kiinduló, mind a kétfajta zajjal (nulla várható értékű, σ=0,5 szórású Gauss zaj, illetve pontszerű zaj, ahol egy pixel 0,2 valószínűséggel változik fekete vagy fehér pixellé) terhelt karakterek képeit mutatja (az ábra első két sora), valamint bemutatja a lineáris PCA és a kernel PCA adott számú főkomponenséből visszaállított karakterképeket is. Minthogy az eredeti képek 256 pixelből állnak, lineáris PCA esetében maximum 256 főkomponens lehetséges. Kernel PCA mellett azonban a jellemzőtér dimenziója a választott kernel függvénytől függően ennél jóval nagyobb is lehet, a sajátvektorok számát pedig a mintapontok száma határozza meg. A példában Gauss kernel függvényt és 300 tanítómintát használtak.
Az ábrából látható, hogy lineáris PCA mellett, ha nem az összes főkomponenst használjuk, az additív zaj mérsékelhető ugyan, de a képek is jelentősen torzulnak, ami a későbbi felismerést nehezíti. A kernel PCA-nál a többdimenziós jellemzőtér biztosítja, hogy a zajt úgy mérsékeljük, hogy közben a képek minősége alig változik.
10.4.3. Független komponens analízis
A független komponens analízis (independent component analysis, ICA) olyan statisztikai módszer, amely adatokban (véletlen változókban, mérési eredményekben vagy akár időfüggvényekben) rejtve meglévő komponensek meghatározására szolgál. A független komponens analízis a megfigyelt többváltozós adatok generálásának egy modelljét definiálja. E modell szerint a rendelkezésre álló többdimenziós adatok egyes komponensei valamilyen ismeretlen változók lineáris vagy nemlineáris „keverékei”, súlyozott összegei, ahol a keverő rendszer szintén ismeretlen. A független komponens analízis feladata ezen rejtett változók meghatározása, feltéve, hogy a rejtett változók statisztikailag függetlenek egymástól.
A független komponens analízis a főkomponens analízis (PCA) kiterjesztésének is tekinthető, amennyiben a megfigyelt adatokban, jelekben itt is valamilyen kitüntetett komponenseket keresünk. A független komponens analízis számos gyakorlati feladat kapcsán felmerül. Ha például időfüggvények független komponensekre való szétválasztása a feladat, szokás vak forrás szeparálásról (blind source separation, BSS) beszélni. Ilyenkor a rendelkezésünkre álló megfigyelt időfüggvények valamilyen források időfüggvényeinek súlyozott összegeiként állnak elő és a megfigyelésekből az eredeti időfüggvényeket szeretnénk visszaállítani. Bár nem időfüggvényekre történő szétbontásról van szó, mégis hasonló feladatról beszélhetünk, ha pl. képek (vagy tetszőleges többdimenziós jelek) keveréke áll rendelkezésünkre, melyekből az eredeti képeket (komponenseket) szeretnénk visszakapni.
Egy komplex jel független komponensekre bontása későbbi feldolgozó lépések (pl. felismerési, osztályozási feladatok) elvégzést is megkönnyítheti. Ilyenkor a független komponens analízis eljárásokat lényegkiemelő eljárásoknak (feature extraction) tekinthetjük. További fontos gyakorlati alkalmazás az ún. vak dekonvolúció (blind deconvolution). Ebben az esetben általában csak egyetlen megfigyelt és egyetlen forrás jelünk van, melyek tipikusan időfüggvények. A megfigyelt jel a forrás jel valamilyen szűrt változata. Lineáris szűrőt feltételezve a megfigyelt jel a forrás jel és a szűrő súlyfüggvényének konvolúciójaként nyerhető, tehát a megfigyelt jel adott időpillanatbeli értéke a forrás jel régebbi értékeinek súlyozott összegeként áll elő. A megfigyelt (szűrt) jelből a forrásjel visszaállítása dekonvolúciós feladat. Amennyiben a szűrő együtthatóit nem ismerjük a jelvisszaállítást vakon kell elvégeznünk. Megfelelő feltételek fennállta esetén a vak dekonvolúció is értelmezhető független komponens analízis feladatként.
A független komponens analízis feladatot egy hétköznapi vak forrás szeparálási feladat kapcsán, az ún. koktélparti probléma kapcsán fogjuk pontosabban definiálni. A koktélparti probléma során beszédjelek keverékéből szeretnénk az egyes beszédjeleket szétválasztani.
Képzeljük el, hogy egy olyan teremben vagyunk, ahol többen beszélnek egyszerre. Amit hallunk az a sok beszéd keveréke. Ebből a beszédkeverékből szeretnénk az egyes különálló beszédjeleket elkülöníteni, hogy megértsük az egyes beszélőket.
Általánosabban a problémát a következőképpen fogalmazhatjuk meg. Adott N skalár értékű, nulla várható értékű, statisztikailag kölcsönösen független jelünk (időfüggvényünk):
, ahol t jelöli az időt. Ezek a jelek lehetnek pl. beszéd hullámforma időfüggvények, ahol minden egyes időfüggvény más-más beszélőtől származik. Az
jeleket közvetlenül nem tudjuk megfigyelni, hanem helyette egy
,…,
jelkészletet figyelhetünk meg, pl. L különböző helyen elhelyezett mikrofon felhasználásával. Minden egyes megfigyelt
jel (mikrofonjel) az egyes beszédjelek súlyozott összegeként áll elő:
(10.79)
ahol az aij együtthatók a súlyozó értékek, melyek pl. a beszélők és a mikrofonok közötti távolságok függvényei. A kevert mikrofonjelekből szeretnénk az eredeti beszédjeleket visszaállítani, vagy legalább becsülni anélkül, hogy az aij együtthatókat ismernénk.
Amennyiben ezen jelek mintavételezett értékeivel dolgozunk, az
, j=1, 2, …, L megfigyelési sorozatokból szeretnénk az
, i=1, 2, …, N független jelsorozatokat visszaállítani, ahol k a diszkrét időindex. Ekkor a jelmodell vektoros formában is felírható:
. (10.80)
ahol A a „keverő” mátrix,
a mátrix j-edik oszlopa.,
pedig a keresett független jelforrások jeleiből álló vektor. A (10.80) összefüggéssel megadott feladat annyiban általánosabb, mint a (10.79) összefüggés, hogy itt feltételeztük, hogy a megfigyeléseinket még egy n(k) additív zaj is terheli. Általában feltételezhető, hogy L ≥ N, tehát legalább annyi megfigyelt jelünk van, mint amennyi a független komponensek száma. Bár az általános feladatnál az additív zaj jelenlétével is kell számolni, a továbbiakban zajmentes esetet tételezünk fel.
A fenti alkalmazási példák mindegyike mögött ott húzódik a következő alapprobléma. Adottak az
valószínűségi változók, melyek az
valószínűségi változók lineáris kombinációiként modellezhetők:
, i=1,2,…N, (10.81)
ahol az
együtthatók valamilyen valós értékű konstansok és ahol feltételezzük, hogy az
valószínűségi változók statisztikailag kölcsönösen függetlenek egymástól. A független komponens analízis feladatoknál mindig feltételezzük, hogy mind az eredeti
valószínűségi változók, mind az
kevert (megfigyelt) valószínűségi változók nulla várható értékűek. A független komponensek és a megfigyelések közötti kapcsolatot vektorosan felírva:
. (10.82)
ahol A a keverési mátrix,
a független komponensek vektora és
a megfigyelések vektora. Az alapproblémánál tehát feltételezzük, hogy a megfigyeléseink zajmentesek, továbbá azt is, hogy pontosan annyi megfigyelésünk van, mint ahány független komponensünk (L=N). Ez utóbbiból következik, hogy A kvadratikus mátrix. A továbbiakban még azt is feltételezzük, hogy A invertálható. Ezekkel az egyszerűsítő feltételezésekkel a független komponensek meghatározása valójában
meghatározását igényli. Ha ismernénk A-t, kiszámíthatnánk az inverzét, amivel a független komponensek közvetlenül meghatározhatók lennének:
. (10.83)
A probléma legegyszerűbb változatánál a megfigyelések a független komponensekből lineáris transzformáció útján származnak és a jelvisszaállítás is egy lineáris transzformáció. A független komponens analízis tehát a jelvisszaállító transzformáció
mátrixának a meghatározását igényli.
A független komponens feladat megoldásánál tehát olyan lineáris transzformációt keresünk, mely minél jobban közelíti az
mátrixot. A nehézséget az okozza, hogy A-t nem ismerjük. Számos valós feladatnál további nehézségeket okoz, hogy a fentiekben megfogalmazott egyszerűsítő feltételezések sem érvényesek.
A fejezetben csak az alapesetre térünk ki, a problémakör általános tárgyalására itt nincs mód. Az általánosabb esetekkel, illetve a nagyon speciális esetekkel a bőséges irodalom pl. [Jut88], [Car94], [Com94], [Kar94], [Bel95], [Ama95], [Gir96], [Kar97], [Kar98], [Hyv00], [Hyv01], [Hyv06] foglalkozik.
A fenti feltételeken túl egy további általános feltételnek is eleget kell tenni: a független komponensek nem lehetnek Gauss eloszlású valószínűségi változók. Ennek a feltételnek az a magyarázata, hogy a független komponens analízis eljárások olyan kritériumok alapján dolgoznak, melyek csak nem Gauss eloszlású valószínűségi változókra alkalmazhatók. Itt érdemes utalni a főkomponens analízis problémára. Míg a főkomponens analízis egy többdimenziós jelet korrelálatlan komponensekre bontja szét, addig a független komponens analízis összetett jelek kölcsönösen független komponenseit próbálja megtalálni, vagy legalább olyan komponenseket keres, amelyek a lehető legnagyobb mértékben függetlenek egymástól. A korrelálatlan komponensekre bontáshoz a bemenet első és másodrendű statisztikai jellemzőinek felhasználása elegendő, az ICA a magasabbrendű statisztikákat is felhasználja.
Gauss eloszlás jellemzésére a magasabbrendű statisztikák alkalmazása nem szükséges, hiszen az első és másodrendű statisztikai jellemzők a Gauss valószínűségi változók teljes statisztikai leírását megadják. Továbbá egy x Gauss eloszlású valószínűségi vektorváltozóra az is igaz, hogy x lineáris transzformációja, (pl. az (10.83) jelvisszaállításnak megfelelő transzformációval) szintén Gauss eloszlású lesz, melyet várhatóérték vektorával és kovariancia mátrixával teljes mértékben tudunk jellemezni. Ennek következménye, hogy a standard független komponens analízis eljárások képtelenek a keverő, illetve a visszaállító mátrixot identifikálni. Ugyanakkor meg kell jegyezni, hogy ha a független komponensek között csak egyetlen Gauss eloszlású található, a feladat megoldható. Azt is mondhatjuk, hogy a független komponens analízis feladat úgy is megfogalmazható, hogy az x valószínűségi vektorváltozók olyan lineáris transzformációját, olyan vetületeit keressük, melyek a lehető legkevésbé Gauss eloszlásúak. A független komponens analízis eljárásoknál ezért a statisztikai függetlenség és a „nemgauss-ság” felcserélhető fogalmak.
A fentiek indokolják a független komponens analízis eljárások formális megfogalmazásait. Olyan eljárásokat keresünk, melyek eredményeképpen kapott komponensek kielégítik a statisztikai függetlenség valamelyik definícióját, vagy melyek eredményeképp kapott komponensek a lehető legkevésbé Gauss eloszlásúak.
Mindkét megközelítés alapján számos eljárást dolgoztak ki. A statisztikai függetlenség mérésére a függetlenség definíciójából indulhatunk ki. A statisztikai függetlenség a valószínűség sűrűségfüggvények vagy eloszlásfüggvények segítségével definiálható. Legyen pl. y1 és y2 két skalár értékű valószínűségi változó és jelölje
illetve
a megfelelő valószínűség sűrűségfüggvényeket. A két valószínűségi változó független, ha a
együttes valószínűségi sűrűségfüggvényük a két sűrűségfüggvény szorzataként felírható:
(10.84)
Ennek felhasználásával könnyen belátható, hogy független valószínűségi változókra fennáll a következő összefüggés is:
(10.85)
ahol
és
tetszőleges abszolút integrálható függvény lehet.
A függetlenség megállapítása a fentieken túl a valószínűségi változók statisztikai jellemzőinek (pl. momentumainak), illetve számos az információelmélet alapján származtatott mennyiségnek az alapján is lehetséges [Hyv01]. Ilyen mennyiségek pl. az entrópia és a kölcsönös információ vagy a Kullback-Leibler divergencia. A nemgauss-ságon alapuló eljárások egyrészt a magasabbrendű momentumokat, elsősorban a kurtózist alkalmazzák, de a nemgauss-ság mérésére is használhatók egyes információelméleti fogalmak, mint pl. a negentrópia. A különböző függetlenség vagy nemgauss-ság mértékek eltérő eljárásokat eredményeznek. Ezen eljárások közül itt csak néhányat mutatunk be. Olyan eljárásokat, melyek neuronháló architektúrával, mintapontokból való iteratív tanulással oldják meg a független komponens analízis feladatot.
A következőkben előbb egy magasabbrendű momentumokon alapuló eljárást, majd az egyik legsikeresebb független komponens meghatározó algoritmust, az ún. FastICA eljárást mutatjuk be. Végül olyan megoldásra is mutatunk példát, ahol a neurális PCA hálózatok nemlineáris változatával becsülhetők a független komponensek. A bemutatott eljárásoknál mindig feltételezzük, hogy mind a kiinduló adatok, mind az eredményként kapott adatok nulla várható értékűek.
Független komponens analízis nemgauss-ság alapján
Annak eldöntése, hogy egy valószínűségi változó Gauss eloszlású-e vagy sem bizonyos magasabbrendű momentumok segítségével is lehetséges. Ilyen magasabbrendű momentum a kurtózis, melyet nulla várható értékű valószínűségi változó esetére a következőképpen definiálhatunk:
. (10.86)
Gauss valószínűségi változóknál a kurtózis nulla, míg olyan eloszlásoknál, melyek a nulla körül csúcsosodnak, de elnyúló farokrésszel rendelkeznek pozitív, lapos sűrűségfüggvény estében pedig negatív a kurtózis. A nemgauss-ság mérésére ezért a kurtózis abszolút értéke vagy négyzete használható. A pozitív kurtózisú eloszlásokat szuper-Gauss, a negatív kurtózisúakat pedig szub-Gauss eloszlásoknak nevezzük. A Laplace eloszlás (kétoldalú exponenciális eloszlás) jó példa a szuper-Gauss eloszlásra, egy egyenletes eloszlású valószínűségi változó pedig szub-Gauss változó. Sok gyakorlati feladatnál a jelforrások szub-Gauss vagy szuper-Gauss jelet szolgáltatnak. A beszédjelek pl. tipikusan szuper-Gauss jelek.
A kurtózis alkalmazásának a független komponensek meghatározásánál a legfőbb előnye, hogy könnyű becsülni. Ha ugyanis a véletlen változó varianciáját egyégnyire tudjuk választani, a kurtózis meghatározása lényegében csak a negyedik momentum számítását igényli. Hátrányos ugyanakkor, hogy a kurtózis nagyon érzékeny a kilógó adatokra, ami viszonylag kevés mintapont alapján történő becslésnél jelentős hibát eredményezhet. A kurtózis nem robusztus mértéke a nemgauss-ságnak.
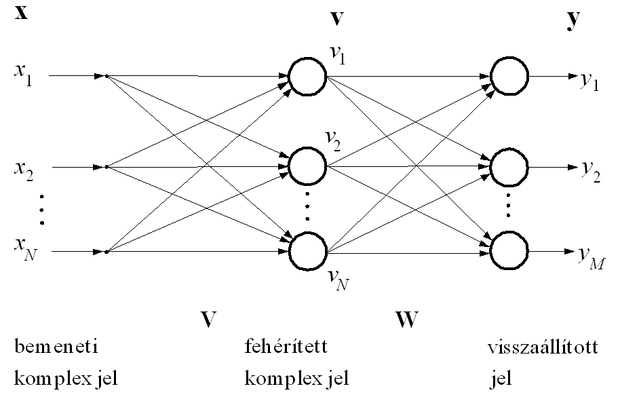
A független komponenseket megadó szeparáló mátrix meghatározása könnyebb, ha előzetesen elvégezzük az adatok ún. fehérítését. A fehérítés a megfigyelések olyan lineáris transzformációja, amelynél a transzformált (fehérített) adatok komponensei kölcsönösen korrelálatlanok és varianciájuk egységnyi.
Ha a fehérített jel
, ahol V a fehérítő transzformáció mátrixa, akkor v autokorrelációs mátrixa egységmátrix lesz:
. A fehérített jel és az eredeti független komponensek közötti kapcsolat ennek megfelelőn:
. (10.87)
Ha feltesszük, hogy a független komponensek varianciája egységnyi, fehérített jel esetén a B keverő mátrix ortogonális lesz: BBT=I.
A fehérített megfigyelésekből kell a visszaállítást elvégeznünk:
. (10.88)
Így egy teljes rangú, de tetszőleges mátrix meghatározása helyett egy egyszerűbb feladatot, egy ortogonális mátrix meghatározását kell megoldanunk. Ha B i-edik oszlopvektorát bi jelöli, akkor az i-edik független komponens a fehérített megfigyelésekből
formában határozható meg.
Minthogy a fehérítés következtében v komponensei korrelálatlanok és egységnyi varianciájúak lesznek, a fehérítés PCA felhasználásával is végezhető. A PCA azonban csak a korrelálatlanságot biztosítja, az egységnyi varianciát nem. A PCA eredményeképpen kapott jel autokorrelációs mátrixa ugyan diagonális lesz, de általában nem egységmátrix, ezért még egy normalizáló lépésre is szükség van. A fehérítő transzformáció mátrixa tehát: V=Λ-1/2Φ, ahol Φ a fehérítendő jel (x) autokorrelációs mátrixának (R) sajátvektoraiból képzett mátrix, Λ pedig R sajátértékeiből álló diagonálmátrix.
A továbbiakban feltételezzük, hogy a független komponens analízis fehérített adatokból dolgozik. Egy független komponens meghatározásánál ezeknek az adatoknak olyan
lineáris kombinációját keressük, hogy a kurtózis maximális vagy minimális értéket vegyen fel. Természetesen a szélsőérték-keresés csak akkor alkalmazható, ha a súlyvektor hossza konstans, ezért feltesszük, hogy
.
A kurtózis maximalizálás (minimalizálás) többféle úton is elérhető, most azonban csak olyan algoritmussal foglalkozunk, ahol a szélsőérték-keresés pillanatnyi gradiens felhasználásával történik. Ekkor olyan iteratív megoldást kapunk, mely megfelelő neurális háló architektúrával megvalósítható. A neurális megoldásnál valójában egy elemi neuront használunk melynek súlyvektora lesz a keresett w.
A fehérített adatok miatt a kritériumfüggvény, melynek a szélsőértékét keressük a következő lesz:
. (10.89)
Ha figyelembe vesszük még a
feltételt, a végleges kritériumfüggvényre a következőt kapjuk:
. (10.90)
ahol F egy büntető tag a súlyvektor hosszára vonatkozó feltétel biztosítására. A büntető tag megválasztására különböző javaslatok születtek. Az eljárás mostani bemutatásánál F konkrét megválasztásával nem foglalkozunk. Meghatározva a kritériumfüggvény pillanatnyi gradiensét – vagyis a kritériumfüggvényből a várhatóérték-képzést elhagyjuk – a súlymódosításra a következő összefüggést kapjuk:
, (10.91)
ahol v(k) az éppen felhasznált fehérített megfigyelés, μ(k) a lépésfüggő tanulási tényező, f pedig a büntető tagból származó komponens, F/2 deriváltja. A büntető tagból származó gradiens komponensnél feltételeztük, hogy
valóban csak
függvénye, és így a gradiense skalár × w formában írható. A módosító tag előjele maximumkeresésnél pozitív, minimumkeresésénél negatív.
Az eljárás konvergenciája a sztochasztikus approximáció alapján bizonyítható [Hyv97]. Bár az iteratív eljárás konvergenciája nem gyors, a pontonkénti tanítás biztosítja a hasonló egyéb pillanatnyi gradiens alapú tanuló eljárásoknál is meglévő tulajdonságot, a változó környezethez való folyamatos adaptálódás képességét. A konvergenciasebességet − ugyancsak hasonlóan az egyéb pillanatnyi gardiens felhasználásával dolgozó eljáráshoz − μ(k) megválasztása jelentősen befolyásolja.
A konvergenciasebesség drasztikusan növelhető, ha fix-pont iterációt alkalmazunk. A fix-pont iterációk származtatásához abból indulunk ki, hogy egy gradiens eljárás stabil pontja csak olyan pont lehet, ahol a gradiens az aktuális súlyvektor irányába mutat, vagyis a gradiens a súlyvektor skalár konstansszorosával egyenlő. Csak ilyen esetben lehetséges, hogy egy gradiens irányú módosító vektort adunk a súlyvektorhoz és annak az iránya mégsem változik [Aga01], [Hea02], [Gra03].
FastICA: egy kurtózis alapú fix-pont ICA algoritmus
A (10.91) súlymódosító összefüggés fix pontjait megkapjuk, ha a súlyváltozás várható értékét vesszük és ezt nullává tesszük. Ha ugyanis az algoritmus konvergens, akkor kialakul egy egyensúlyi állapot, amikor a súlymódosítások várható értéke nulla. A diszkrét időindexet elhagyva a súlymódosítás várható értéke:
. (10.92)
Az ilyen egyenletek megoldására számos determinisztikus iteratív eljárás létezik. Nagyon gyors iterációt kapunk, ha az (10.92) összefüggést a következő formában írjuk fel:
. (10.93)
Most csak w iránya érdekes számunkra, a vektor normája lényegtelen. Ezért az összefüggésben szereplő skalár konstans hatása egy explicit normalizálással kiváltható.
Az alábbiakban az algoritmus fő lépéseit mutatjuk be, előbb egyetlen, majd több független komponens meghatározására.
Tételezzük fel, hogy a megfigyelhető mintapontok független komponensek lineáris kombinációiként jöttek létre és a mintapontokon a fehérítést elvégeztük. Ekkor egy független komponens az alábbi lépések alkalmazásával határozható meg:
1. Válasszunk véletlenszerűen egy w(0) kezdeti súlyvektort és legyen a diszkrét lépésindex k=1.
2. Legyen
,
ahol a várhatóértéket kellően nagyszámú (pl. 1000) v mintapont alapján becsüljük.
3. Normalizáljuk w(k)-t úgy, hogy osszuk el w(k)-t a normájával.
4. Ha
közel 1, w(k)-t tekintsük eredménynek, egyébként legyen k=k+1 és menjünk vissza a 2. lépéshez.
A kapott w(k) vektor az ortogonális keverő mátrix egyik oszlopvektora lesz. Ez azt jelenti, hogy
megadja az egyik független komponens becslését. Az eljárás igen kedvező tulajdonsága, hogy kevés (tipikusan 5-10) iterációs lépés elegendő, hogy a mintapontok által biztosított maximális pontosságú becslést kapjunk.
A fenti algoritmus egyetlen független komponens meghatározására alkalmas. A független komponens analízis feladatoknál azonban legtöbbször az összes vagy legalábbis több független komponens meghatározására van szükség. Több független komponens meghatározása az előbbi algoritmus segítségével úgy lehetséges, ha az algoritmust egymás után többször lefuttatjuk. A többszöri lefuttatatásnál azonban biztosítani kell, hogy ne ugyanazt a független komponenst határozzuk meg többször. Ehhez egy ortogonalizáló vetítést kell beiktatnunk az algoritmus lépései közé. Itt emlékeztetni szeretnénk arra, hogy a fehérítés következtében a keverő mátrix ortogonális. Ezért a független komponenseket egyenként becsülhetjük, ha az aktuális w(k) megoldást egy olyan térre vetítjük, amely ortogonális a B keverőmátrix eddig megtalált oszlopvektoraira.
Legyen
az eddig megtalált oszlopvektorokból felépített mátrix. A fenti algoritmusban a 3. lépést cseréljük ki a következőre:
3. Legyen
, majd normalizáljuk w(k)-t.
Ezen a módosításon kívül egy hasonló vetítésre szükség van a kezdeti súlyvektor felvételénél is.
Hogy elkerüljük az előző vektorok (tehát
) becslési hibájának hatását a későbbi vektorok becslésénél, a fenti vetítést csak az algoritmus első néhány iterációjában alkalmazzuk. Ha az algoritmus már közelítőleg megtalálta a keverőmátrix egy oszlopát, akkor már egy fix pont vonzáskörzetében vagyunk, ahonnan a megfelelő pontba történő konvergencia már biztosított.
Az algoritmus bizonyítottan konvergens, sőt a konvergenciasebességre is lehet állítást megfogalmazni. A részletek [Hyv97]-ben és [Hyv01]-ben megtalálhatók.
Megjegyezzük, hogy a bemutatott gyors ICA eljárás csak egy a hasonló fix pont algoritmusok közül. Hasonló eredményeket a nemgauss-ság más megfogalmazása alapján is származtathatunk. Így pl. a negentrópia alapján is származtatható FastICA algoritmus, melynek részletes bemutatása [Hyv01]-ben található.
Független komponens analízis nemlineáris PCA alkalmazásával
Az eddigiek alapján látható, hogy a független komponensekre bontás a (fehérített) megfigyelések lineáris transzformációjával lehetséges, ahol a transzformáló mátrix meghatározása nemlineáris feldolgozó lépéseket is igényel. Ez veti fel azt a gondolatot, hogy érdemes a PCA algoritmus nemlineáris változatával próbálkozni.
A (10.88) összefüggés szerint egy olyan B mátrixot keresünk, amely a fehérített megfigyelésekből visszaállítja az eredeti független komponenseket. Konstruáljunk ezért egy olyan egyrétegű neurális hálót, melynek súlyvektorait a PCA hálózatoknál alkalmazott Oja altér szabály nemlineáris változatával tanítjuk. A súlymódosító összefüggésünk ennek megfelelően legyen a következő:
(10.94)
Itt W a többkimenetű háló összes súlyvektorából, mint sorvektorból felépített súlymátrix, v a fehérített megfigyelésvektor, y a háló kimeneti vektora, g(y) pedig egy olyan vektort jelöl, melynek i-edik komponense g(yi), ahol g(.) egy megfelelő nemlineáris függvény. Megmutatható, hogy a (10.94) összefüggés egy olyan sztochasztikus gradiens algoritmus, amely a
kritérium szélső értékét keresi, azzal a feltétellel, hogy W ortonormált (M a kimenetek száma). Ha f(t)=t4/4, a kritérium a negyedik momentumok összegét jelenti, és minthogy a sztochasztikus gradiens eljárás miatt g(t) az f(t) függvény deriváltja, g(t)=t3. A nemlineáris függvény ilyen megválasztása mellett (10.94) valóban a negyedik momentumok összegének szélsőértékét biztosító, ortonormált W-t eredményezne, de az algoritmus nem stabil. Stabil algoritmust nyerünk, ha pl. a g(t)=tanh(t) függvényt választjuk, amelynek Taylor-soros közelítésében a t3 tag domináns lehet.
Fehérített jelek és ortogonális szeparáló mátrix mellett igaz, hogy
, ezért, ha a negyedik momentumok összegét,
-t minimalizáljuk a szub-Gauss jelekre, ill. maximalizáljuk a szuper-Gauss jelekre, akkor a
(10.95)
kritériumfüggvény maximumát biztosító megoldást kapunk, vagyis most is a kurtózis alapján dolgozó algoritmust nyertünk.
A nemlineáris PCA háló tehát egy Oja altér hálóhoz hasonló felépítésű azzal az eltéréssel, hogy nemlineáris neuronokból épül fel, ahol a nemlinearitást célszerűen a szokásos tangens hiperbolikusz függvényre kell választani. A háló azonban csak a tanulási fázisban működik nemlineáris hálóként, hiszen a független komponenseket a fehérített adatok lineáris transzformációjával nyerhetjük. A visszaállító mátrix meghatározása azonban nemlineáris művelet, ezért a tanulási fázisban szükség van a nemlineáris neuronokra.
A nemlineáris PCA hálózatoknak is több változatát dolgozták ki. Ezek között említést érdemel az ún. bigradiens algoritmus, mely egyszerűsítést jelent az Oja nemlineáris PCA szabályhoz képest. A bigradiens algoritmus súlymódosító összefüggése a következő [Wan96b]:
(10.96)
ahol α egy konstans együttható, melynek értékét a [0,5, 1] intervallumból kell választani, a g függvénykapcsolat pedig azt jelöli, hogy egy g függvényt a Wv vektor komponenseire külön-külön alkalmazzuk.
A bigradiens algoritmus előnye, hogy az (10.94) összefüggésben szereplő
számítását nem igényli.
A nemlineáris PCA algoritmuson alapuló megoldás, mint kétlépéses szeparáló algoritmus neurális architektúrával is megvalósítható. A háló két rétegből áll (10.13 ábra). Az első, lineáris réteg a fehérítést végzi, ennek a rétegnek a súlyait a
. (10.97)
összefüggés szerinti tanítással határozhatjuk meg [Plu93], ahol x a tényleges bemeneti adat. A második réteg, melynek súlyait a (10.94) vagy a (10.97) összefüggés szerinti nemlineáris Hebb szabállyal tanítjuk, a fehérített v vektorokon dolgozik.
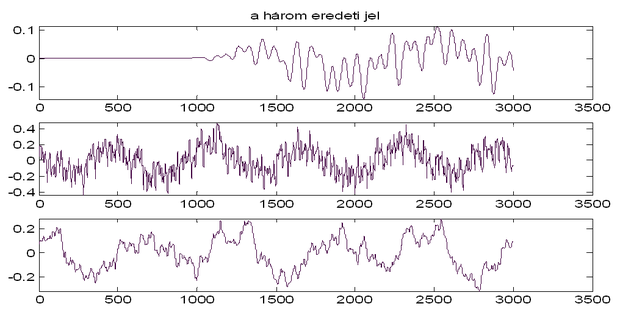
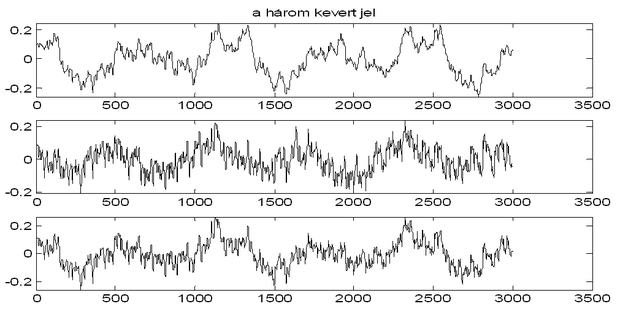
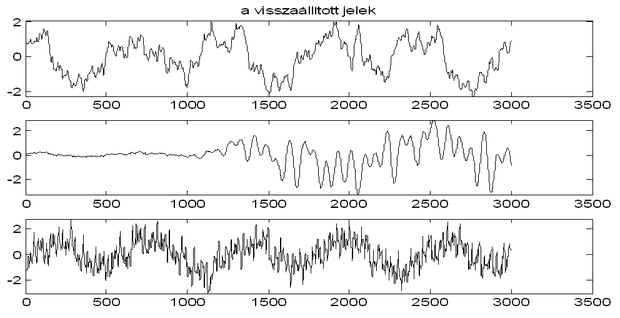
A független komponens analízis működését két példán illusztráljuk. Az első példa (10.14 ábra) három időfüggvény lineárisan súlyozott keverékeiből indul ki. Az ábrán a három kiinduló időfüggvényt, ezen időfüggvények keverékeit, valamint a három visszaállított jelet láthatjuk. A 10.15 ábra kétdimenziós jelek (képek) független komponenseinek meghatározására mutat példát.
Mindkét példa jól illusztrálja a független komponens analízis eljárások két „hiányosságát”. Egyrészt nem tudjuk megmondani, hogy az eljárások milyen sorrendben állítják elő a független komponenseket. Másrészt az eredmények csak egy skalár szorzótényezőtől eltekintve lesznek egyértelműek. A független komponensként egy eredeti jel valamilyen skalárszorosát kaphatjuk. Ha rögzítjük a jelek varianciáját például egységnyire, még akkor is visszakaphatjuk az egyes eredeti komponensek (−1)-szeresét. Ezt figyelhetjük meg a 10.14 ábrán a második időfüggvénynél, valamint a képvisszaállításnál a fatörzs esetében, ahol az eredeti kép helyett annak negatívját kaptuk eredményül.
A független komponens analízis feladat megoldására a fentiekben röviden bemutatott eljárásokon túl számos egyéb javaslat született. Ezek az eljárások általában a feladat más megfogalmazásából származtathatók. További olyan változatokat is kidolgoztak, melyek az itt bemutatott alapfeladaton túl általánosabb eseteket próbálnak megoldani. Ilyen eset lehet, ha a megfigyeléseinket zaj terheli, továbbá, ha a keverőmátrix nem konstans. A független komponens analízis eljárásoknak kidolgozták olyan változatait is, melyek valamilyen mértékben kezelni tudják azon eseteket is, amikor kevesebb megfigyelésünk van, mint ahány független komponens szeretnénk meghatározni.

Feladatok
10.1 Mutassa meg, hogy a Kohonen hálónál alkalmazott tanítási összefüggés (10.5 egyenlet) a normalizált Hebb szabály.
10.2 A [0,5 3,5] × [0,5 3,5] tartományon egyenletes eloszlású, kétdimenziós adathalmaz feldolgozására topologikus leképezést biztosító Kohonen hálót alkalmazunk. A háló − kétdimenziós rácsban elhelyezve − 9 neuront tartalmaz az [i, j] pozíciókban, ahol i,j=0,1,2. Milyen súlyvektorok kialakulása várható a háló tanítása után?
10.3 Milyen súlyvektorokat kapunk a tanítás végén, ha az előző feladat adathalmazát egy 9 neuront lineáris elrendezésben tartalmazó Kohonen hálónak tanítjuk. A neuronok pozíciói: 1, 2, 3, . . . , 9.
10.4 Mutassa meg, hogy az Oja szabállyal tanított háló súlyvektora egyensúlyi helyzetben a bemenet autokovariancia mátrixának sajátvektora.
10.5 A GHA (Sanger) háló csak előrecsatoló összeköttetéseket használ. Ezzel szemben az APEX algoritmus mind előrecsatoló, mind oldalirányú kapcsolatokkal rendelkezik. Mutassa meg, hogy a két eltérő hálózat-architektúra a megfelelő tanulási algoritmussal azonos súlyvektorokhoz (wi) konvergál.
10.6 Miért van szükség minimum 5 rétegű hálózatra, ha nemlineáris adattömörítést szeretnénk végezni?
10.7 Kernel PCA esetére, Gauss kernel mellett határozza meg a jellemzőtérbeli tömörített reprezentáció bemeneti térbeli közelítő megfelelőjét. Adja meg a gradiens eljárással dolgozó jelvisszaállítás algoritmusát.
10.8 Mutassa meg, hogy két független komponens súlyozott összegeiből kapott kevert adatokból kiindulva a kurtózis maximalizálása útján valóban megkapjuk a független komponenseket, ha szuper-Gauss komponensekből indulunk ki és kikötjük, hogy az eljárás eredményeképpen kapott adatok varianciája legyen egységnyi. A feladatot, mint feltételes szélsőérték-kereső problémát oldja meg.
10.9 Adja meg, hogy milyen feltételek mellett tekinthető a nemgauss-ság és a függetlenség ekvivalens fogalmaknak.
![Egy egyszerű példa a kernel PCA működésének illusztrálására [Sch96c]. (dr. Klaus-Robert Müller hozzájárulásával).](/mi_almanach/sites/default/files/books/528/files/kepek/10-10_a.png)





![A kernel PCA zajtalanító hatása [Mik99]. (dr. Klaus-Robert Müller hozzájárulásával)](/mi_almanach/sites/default/files/books/528/files/kepek/10-11.png)