Az előzőekben bemutatott konkrét neuronháló architektúrákon túl számos további lehetőség áll rendelkezésünkre neuronháló alapú dinamikus rendszerek létrehozására. Ezek a lehetőségek azon a már említett megközelítésen alapulnak, hogy statikus nemlineáris és dinamikus lineáris rendszerek különböző struktúrájú összekapcsolásával különböző nemlineáris dinamikus modellek nyerhetők.
Láttuk, hogy a statikus tulajdonságú hálózatok dinamikussá tétele során a leggyakrabban használt lehetőség késleltető sorok (tapped delay line), illetve visszacsatolások alkalmazása. Természetesen az így keletkező struktúrák tanításához legtöbbször egy új tanító algoritmus megalkotása is szükséges. Erre az előzőekben több példát is láttunk. A módszereket alapvetően három csoportba sorolhatjuk:
-
dinamika beépítése a feldolgozó elemekbe (tulajdonképpen lokális visszacsatolás),
-
visszacsatolások kialakítása a hálózaton belül (globális vagy lokális visszacsatolás),
-
egybeépítés hálózaton kívüli dinamikával.
Valójában mindhárom fenti lehetőség statikus-nemlineáris és dinamikus-lineáris részek − különféle kombinációkban történő − összekapcsolását jelenti.
Az első lehetőséget sokan vizsgálták, elsősorban a hibavisszaterjesztéses algoritmussal tanított többrétegű perceptron hálózatból kiindulva (ld. pl. a FIR- MLP hálót). Ennek a módszernek a hátránya az, hogy a többrétegű háló önmagában is nagy számításigényű tanítása a dinamikus elemek beépítése miatt még nagyobb számítási kapacitást igényel, az így kapott háló tanítása meglehetősen lassú lesz.
A második lehetőségre jellegzetes példaként két rekurzív hálózat-architektúrát a megfelelő tanítási algoritmusokkal szintén bemutattunk.
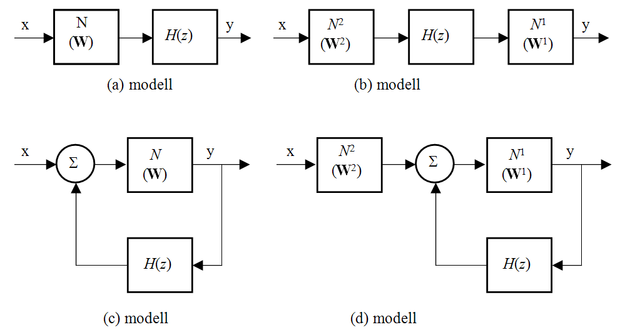
A továbbiakban az utolsó lehetőséget vizsgáljuk, mivel az így felépíthető rendszerek igen bonyolultak is lehetnek, ugyanakkor strukturált felépítésük miatt viszonylag könnyebben értelmezhetők. Bár ezekre a lehetőségekre már utaltunk, a lineáris dinamikus és nemlineáris statikus rendszerek kombinációjaként származtatott elrendezések vizsgálata az eddigiektől kissé eltérő, általános megközelítés bevezetését teszi lehetővé: a tanítást, mint az általános érzékenységvizsgálat eredményét felhasználó eljárást értelmezi. Ezt a megközelítést Kumpati Narendera cikkeit [Nar90] és [Nar91] követve a 8.12 ábrán látható elrendezésekhez kapcsolódóan fogjuk bemutatni.
Az ábra négy elrendezést mutat, melyek mindegyike statikus nemlineáris leképezést megvalósító neuronháló(k)ból és lineáris dinamikus rendszerből áll. Az ábrán H(z) jelöli a lineáris dinamikus részrendszereket, N,
pedig neurális hálózattal megvalósított nemlineáris statikus elemeket, ahol W jelöli a hálózat súlymátrixát. Ezeket az összetett struktúrákat általánosított neurális hálózatoknak (generalized neural network) nevezzük.
8.5.1. A parciális deriváltak számítása
A statikus MLP hálózatok tanítására alkalmazott hibavisszaterjesztéses algoritmus (5. fejezet) kiszámítja a hálózat négyzetes kimeneti hibájának a hálózat paraméterei (súlyai) szerinti parciális deriváltjait. Erre azért van szükség, mert az alkalmazott gradiens alapú algoritmus ez alapján számítja a súlymódosításokat. Az algoritmus a rétegeken keresztül visszafelé haladva a láncszabály alkalmazásával számítja ki az egyes deriváltakat, ami tulajdonképpen azt jelenti, hogy mindig kiszámolja az egyes rétegek kimeneteinek a réteg bemenetei szerinti deriváltjait is.
Amikor a statikus hálózatot egy összetett struktúra részeként akarjuk használni és az egész rendszert akarjuk tanítani, akkor – amint a következő részben majd látjuk – szükség lehet a neurális alaprész kimeneteinek a bemenetei szerinti parciális deriváltjaira is. Ezeket a deriváltakat a hibavisszaterjesztéses algoritmushoz nagyon hasonló módon, a hálózat rétegein visszafelé haladva tudjuk kiszámítani.
A módszert a hibavisszaterjesztéses algoritmusnál is használt, az 4.1. ábrán látható kétrétegű, két kimenettel és egy háromelemű rejtett réteggel rendelkező hálózaton demonstráljuk. Példaként a
parciális derivált számítását végezzük el:
(8.58)
A 4.2. alfejezetben bemutatotthoz hasonló módon itt is bevezethetők az egyes rétegek neuronjainak lineáris kimeneteihez tartozó kimeneti deriváltak (a hálózat kimenetének a neuronok lineáris kimenetei szerinti deriváltjai). Ha az (4.4)-es képlettel definiált származtatott hibagradiens számításakor a kimeneti hiba (
) helyére egységet helyettesítünk, akkor a további visszaterjesztő lépések során a
mennyiségek sorra a kimenet parciális deriváltjait fogják tartalmazni az adott neuron lineáris kimenete szerint. Ezért a közönséges statikus hibavisszaterjesztéses algoritmus felhasználható a kimenet parciális deriváltjainak számításánál (közvetlenül azonban csak egy kimenet esetén). A j-edik bemenethez tartozó parciális derivált az első réteg neuronjainak az adott bemenethez tartozó súlyai (
) és a
mennyiségek lineáris kombinációja lesz.
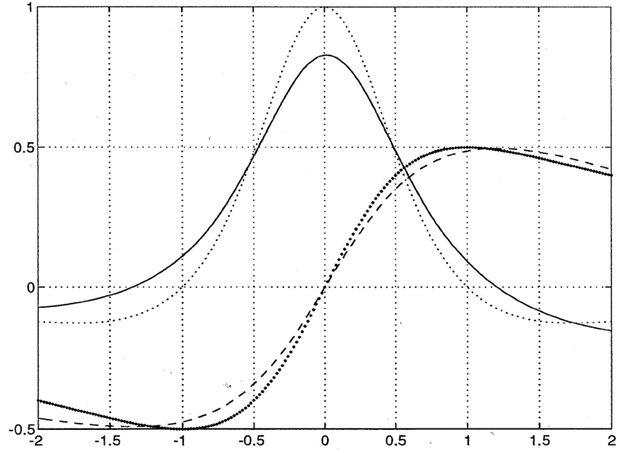
A 8.13 ábra a fenti módszerrel meghatározott parciális derivált számítását mutatja egybemenetű és egykimenetű hálózat esetén (ekkor persze a parciális derivált közönséges deriváltat jelent). Az ábrán a tanító jel és a hálózat válasza is látható 200 tanító ciklus után. (A konkrét példánál a 200 tanító ciklus még kevés). A sűrűn pontozott vastagabb vonal jelöli a megtanulandó függvényt, a szaggatott a hálózat válaszát. A folytonos vonal a fenti módon számított gradiens, míg a ritkán pontozott vékonyabb vonal a megtanulandó jel valódi deriváltja.
8.5.2. Neurális hálózatot tartalmazó összetett struktúrák tanítása
Elsőként a 8.12 ábrán felvetett legegyszerűbb, (a) modellt vizsgáljuk. Ez egy statikus neurális hálózatot és ennek kimenetére kapcsolt (ismert) lineáris dinamikus elemet (szűrőt) tartalmaz. Mivel már ebben az egyszerű modellben sem a neurális rész kimenetén keletkezik a hiba, a statikus hibavisszaterjesztés nem használható. (A kimeneten kapott hibát közvetlenül nem használhatjuk föl a hálózat tanítására. Gondoljunk csak a legegyszerűbb esetre, ha a kimeneti tag nem is dinamikus, hanem csak egy konstans szorzó. Ha a konstans értéke negatív és a kimeneti hibát használva statikus tanító algoritmussal próbáljuk tanítani a hálózatot, akkor az mindig pontosan a helyi gradienssel megegyező irányban, azaz az optimumtól távolodva fogja változtatni a hálózat súlyait.) Erre az esetre dolgozták ki az ún. dinamikus hibavisszaterjesztéses algoritmust.
A statikus esettől eltérően most mind a kimeneti kívánt értékek, mind a kimeneti hibavektor időfüggvények. Célunk most is a kimenti négyzetes hiba minimalizálása, és most is gradiens alapú módszert használunk.
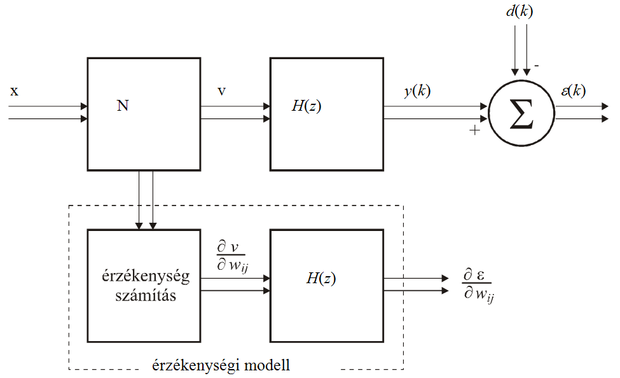
Az 8.14 ábra több-bementű−többkimenetű hálózatra mutatja a gradiensszámítás elvét. Az ábra jelöléseivel az alábbi eredményre juthatunk:
(8.59)
A
parciális deriváltak minden lépésben számíthatók a statikus hibavisszaterjesztéses módszerrel. A képletet értelmezve azt láthatjuk, hogy az egymás után, statikus visszaterjesztéssel kapott súlyváltoztatásokat át kell engedni (szűrni) a kimeneti lineáris dinamikán. Ezt mutatja az 8.14 ábrán az érzékenységi modellnek nevezett rész. Ha az előbbi egyszerű dinamikamentes példára vizsgáljuk az eredményt, láthatjuk, hogy a kimeneti elemen átszűrve a súlyváltoztatásokat, valóban jó eredményre jutunk.
A 8.12 (b) ábrán felvetett rendszer
jelű neurális hálózata a kimeneten helyezkedik el, így statikus algoritmussal tanítható. Az
jelű hálózat gradiense az alábbi összefüggés szerint határozató meg:
(8.60)
A fenti kifejezésben a
differenciálhányados az előző részben meghatározott módon
(ld. (8.58) összefüggés), míg a
derivált az (a) rendszernél bemutatott módon számítható.
A 8.12 (c) modell egy lineáris rendszerrel visszacsatolt neurális hálózatot tartalmaz. A modell kimenete ennek megfelelően:
(8.61)
Az eddigiekhez hasonlóan most is igaz, hogy:
, (8.62)
A visszacsatolás miatt az itt adódó egyenlet egy differenciaegyenlet; a keresett deriváltak függnek saját korábbi értékeiktől is.
, (8.63)
ahol a
értékek statikus visszaterjesztéssel, a
Jacobi mátrix (ennek elemei a kimenetek deriváltjai a bemenetek szerint) pedig az (a) modellnél bemutatott módon számíthatók (
a pillanatnyi deriváltat jelöli, míg a
az "időben" számítottat).
A (d) modell a legösszetettebb a négy közül. Az
jelű hálózat a (c) modellnél bemutatott módon tanítható, míg az
tanításához szükséges hibaderiváltakra a következő formula származtatható:
, (8.64)
Mind a (c), mind a (d) modell tanítására kapott eredmények úgy is értékelhetők, hogy a statikus visszaterjesztéssel kapott deriváltakat át kell engedni egy, a beágyazó rendszer által meghatározott dinamikus rendszeren [Nar90].
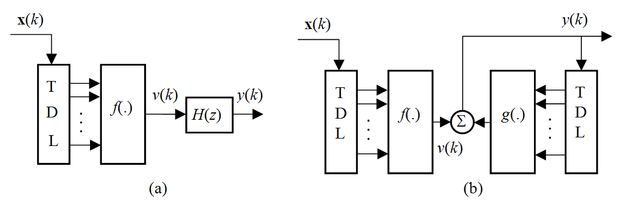
A 8.15 ábra négy konkrét rendszert mutat, amelyek tanítása az előzőkben bemutatott elvek alkalmazásával elvégezhető.
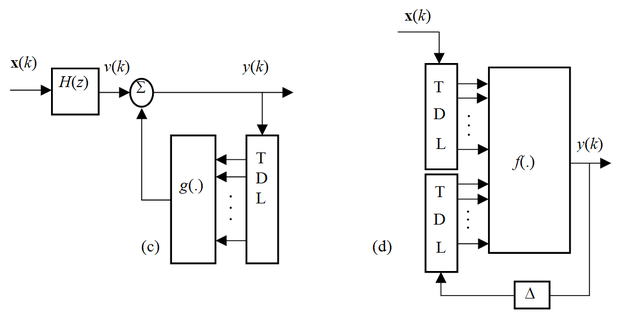
Az egyes architektúráknál f(.) és g(.) statikus nemlineáris leképezéseket jelöl, melyeket valamilyen neuronhálóval valósíthatunk meg. A TDL blokkok késleltető láncot jelölnek a késleltető fokozatok közötti megcsapolásokkal, H(z) pedig egy lineáris dinamikus rendszert, amely lehet előrecsatolt (FIR) vagy visszacsatolt (IIR) típusú is. E struktúráknak az az érdekessége, hogy a nemlineáris leképezéseket statikus hálókkal megvalósító f(.) és g(.) blokkok bemenetén megcsapolt késleltető sorokat találunk, tehát ezek a hálórészek önmagukban is dinamikus nemlineáris rendszerek (pl. FIR-MLP-k). Ennek megfelelően az (a) architektúra egy NFIR típusú dinamikus neuronháló és egy lineáris szűrő sorbakapcsolásából áll. A (b) elrendezésben két NFIR típusú háló található; az egyik az előrecsatoló, a másik a visszacsatoló ágban. A (c) elrendezés hasonló a (b)-hez, azzal a különbséggel, hogy az előrecsatoló ágban lévő NFIR háló helyett egy lineáris szűrő szerepel, míg a (d) elrendezés a fejezet elején bemutatott NARX modell. Ezek az architektúrák is azt illusztrálják, hogy neuronháló alapú nemlineáris dinamikus rendszermodelleket nagyon sok változtaban tudunk konstruálni. Az itt bemutatott architektúrák tanítása a megfelelő dinamikus neuronhálók és az összetett struktúrák tanításánál bemutatott eljárások kombinálásával végezhető el.