8.6. Dinamikus hálók alkalmazása
A dinamikus neurális hálózatokalkalmazása igen szerteágazó. A hálók legfontosabb alkalmazási területei bonyolult ipari, gazdasági, pénzügyi, stb. rendszerek modellezéséhez, irányításához, illetve az ilyen komplex rendszerek viselkedésének előrejelzéséhez kapcsolódnak. Általánosságban elmondható, hogy a dinamikus neuronhálók mindazon területeken sikerrel alkalmazhatók, ahol a hagyományos eszközökkel történő feladatmegoldás nem vagy nehezen lehetséges, és ahol a neuronhálók alkalmazásához elengedhetetlenül szükséges megfelelő mintakészlet rendelkezésre áll vagy megszerezhető. Egyfelől tehát a rendelkezésre álló ismeret, tudás jellege, másfelől a feladat komplexitása szabja meg, hogy a neuronhálók adott feladat megoldásában sikerrel alkalmazhatók-e vagy sem.
A dinamikus hálók alkalmazási körét két fő szempont határozza meg: egyrészt a dinamikus hálók képessége, másrészt az, hogy milyen előnyök várhatók a neuronhálók alkalmazásától. Láttuk, hogy a statikus neuronhálók több típusára igaz, hogy univerzális approximátorok, tehát képesek tetszőleges folytonos nemlineáris leképezés tetszőleges pontosságú közelítésére. A dinamikus neuronhálók – bármilyen alkalmazási területet is nézünk – sikerüket az általános modellező képességüknek köszönhetik. Előnyük – és részben hátrányuk is –, hogy a megoldandó feladatról viszonylag kevés háttérismeret birtokában is alkalmazhatók. Téves nézet azonban az, hogy mivel egy neuronháló fekete doboz modellt valósít meg, itt nincs is szükség a megoldandó feladat részletes megismerésére. Miközben a fekete doboz modell a bemeneti-kimeneti mintapontok vagy mintaszekvenciák alapján létrehozható, a megoldás minőségét és a megfelelő minőségű megoldás elérésének nehézségét is döntően befolyásolja, hogy milyen jellegű és mennyi ismeret áll rendelkezésünkre.
A dinamikus hálók alapvetően a statikus hálók kiterjesztései révén származtathatók, ahol a fő képességeket a regresszor és a nemlineáris leképezés együttesen határozzák meg. Megfelelően megválasztott regresszor és az univerzális approximátor képesség biztosítja, hogy a dinamikus neuronhálókat, mint univerzális nemlineáris dinamikus rendszermodellező eszközöket tekintsük.
A következőkben előbb a dinamikus rendszerek modellezésének néhány általános kérdését foglaljuk össze röviden, majd a neurális hálózatok dinamikus feladatokra történő alkalmazásánál felmerülő fontosabb kérdésekkel foglalkozunk, végül néhány mintapéldát mutatunk be.
Az identifikáció, mint alapfeladat célja létrehozni a vizsgált rendszer egy modelljét, amely adott feltételek mellett, adott pontossággal közelíti az eredeti rendszer viselkedését.
Egy rendszermodellezési feladat megoldásánál a következő főbb lépések különböztethetők meg:
-
a modellezés céljának meghatározása,
-
kiinduló a priori információ begyűjtése a modellezendő rendszerről,
-
a modellstruktúra megválasztása,
-
kísérlet-tervezés és adatgyűjtés,
-
modell paraméterbecslés,
-
a modell kiértékelése.
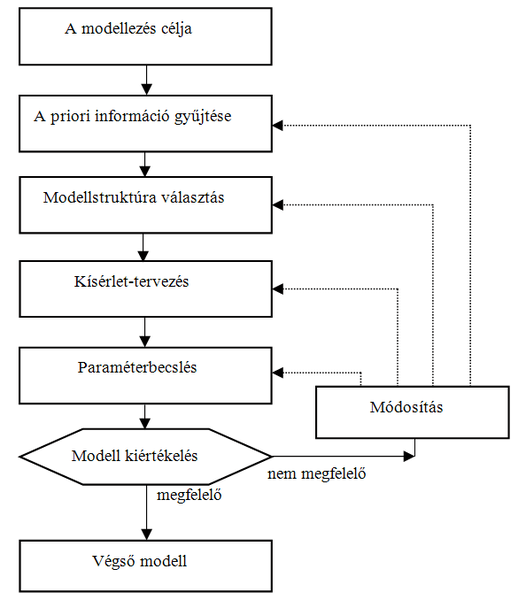
A 8.16 ábra egyrészt a fenti lépések kapcsolatát, másrészt azt mutatja, hogy a modellezés iteratív folyamat.
A struktúra rögzítését követően, a kísérletek eredményeképpen kapott további ismeretek felhasználásával tudjuk a modell szabad paramétereinek értékét meghatározni, a paraméterbecslési feladatot megoldani. Az így kapott modell kiértékelése alapján dönthetünk, hogy a modellünk a kitűzött célnak megfelel-e vagy finomítani, pontosítani kell. Ez utóbbi esetben a modellezési folyamat valamely korábbi lépéséhez vissza kell térni. Ez jelentheti a modell struktúrájának módosítását, további ismeret begyűjtését − melyhez akár új kísérlettervezésre is szükség lehet −, vagy a paraméterbecslési eljárás módosítását.
Azzal, hogy neuronhálós modellt építünk a fenti kérdések egy részét eleve eldöntöttük, hiszen a neuronhálós modell struktúráját a neuronháló típusának meghatározásával részben rögzítjük is. Neuronhálós modellezésnél azt azonban figyelembe kell venni, hogy a modell struktúráját döntően a modellező eszköz és nem a modellezendő rendszer szabja meg. Ezért strukturális modell létrehozására − ahol cél, hogy a modell struktúrája minél inkább hasonló legyen a modellezendő rendszer struktúrájához − lényegében nincs lehetőség; a neuronhálós modell viselkedési modell. A viselkedési modell a modellezendő rendszer bemeneti-kimeneti viselkedését tudja minél pontosabban leírni anélkül, hogy a modell struktúrája akárcsak hasonlítana is a modellezendő rendszer struktúrájához. Ez azt jelenti, hogy neuronhálós modellezésnél még akkor sem tudunk strukturális modellt létrehozni, ha egyébként az ehhez szükséges ismeret birtokában vagyunk. A neuronhálós modellek fekete doboz (black box) modellek, melyek csupán kívülről nézve jellemzik a modellezendő rendszer viselkedését.
Neuronhálós modellezésnél a modellstruktúra választás alapvetően arra a kérdésre ad választ, hogy a lehetséges általános struktúrák melyikét alkalmazzuk. A struktúraválasztás első kérdése, hogy a modellezendő rendszer statikus vagy dinamikus modellel írható-e le kellő pontossággal.
Amennyiben statikus rendszermodellezési feladattal állunk szemben, az előző fejezetekben bemutatott neuronháló típusok közül választhatunk. A struktúraválasztás a típusválasztáson túl a háló méretének – pl. egy MLP rejtett rétegében a neuronok számának – a megválasztását is jelenti. Az ezzel kapcsolatos nehézségekkel és lehetőségekkel az előző fejezetekben foglalkoztunk.
Dinamikus feladatoknál a struktúraválasztás jóval nehezebb: egy dinamikus neurális hálózat által biztosított leképezésben mind a regresszorvektort, mind a dinamikus háló komplexitását (pl. a rejtett rétegek számát, a rejtett réteg(ek) méretét vagy a bázisfüggvények számát, stb.) meg kell határozni. A regresszorvektor-választás egyfelől a nemlineáris dinamikus modellosztály megválasztását jelenti, másfelől a modell-fokszám meghatározását is igényli.
A modellosztály megválasztása elsődlegesen a priori információ alapján lehetséges. Amennyiben van olyan előzetes ismeretünk, amely alapján kiválasztható a modellosztály, valójában már nem fekete doboz, hanem sokkal inkább szürke doboz(grey box) modellezéssel van dolgunk. Megfelelő a priori információ nélkül azt az általános elvet követhetjük, hogy mindig a lehető legegyszerűbb, a feladatot még megfelelő minőségben megoldó modellosztályt célszerű választanunk. Ez azt jelenti, hogy amennyiben dinamikus nemlineáris modellre van szükségünk, célszerű az NFIR struktúrával kezdeni és csak akkor áttérni komplexebb modellosztályra, ha az egyszerűbbel a feladat megfelelő minőségben nem oldható meg.
A fejezet elején áttekintett modellosztályok közül az NFIRés a NARXstruktúrák kitüntetettek, mivel ezek előrecsatolt architektúrák, így alkalmazásukkal a visszacsatolt struktúráknál jelentkező stabilitási kérdések nem merülnek fel. A visszacsatolt nemlineáris rendszerek stabilitási kérdéseivel a könyvben nem foglalkozunk. Az érdeklődő olvasó az irodalomban (pl. [Nar05], [Suy99], [Hay99], [Gup03], stb.) tájékozódhat.
A modellosztály megválasztását követően a struktúra meghatározása a modell-fokszám meghatározását igényli. A bemenet-kimenet reprezentációk mellett a modell-fokszám a regresszorvektor konstrukciójánál figyelembe vett régebbi bemeneti és/vagy kimeneti, stb. értékek számát jelenti. Mivel a modell-fokszám előzetesen általában nem ismert, célszerű különböző modell-fokszámok mellett különböző komplexitású modellek létrehozása és valamilyen kritérium szerinti kiértékelése. A kérdés egy lehetséges intuitív megközelítése, ha egyre növekvő komplexitású modelleket hozunk létre és értékelünk ki, például az átlagos négyzetes hiba kritérium alapján. Már a statikus hálóknál láttuk azonban, hogy a modell komplexitásának növelésével monoton módon csökkenthető (a tanítópontokban) a modellezés hibája, miközben az általánosítóképesség romolhat. A túl nagy komplexitás dinamikus hálóknál is a tanítópontokhoz való túlzott illeszkedést eredményezheti, miközben az általánosítóképességet ronthatja.
A tanítópontokban meghatározott hiba önmagában nem elegendő a megfelelő modellkomplexitás meghatározására. Ehhez olyan kritériumfüggvények alkalmazása szükséges, melyek a tanítópontokban meghatározható modellezési hiba mellett a modell komplexitását is figyelembe veszik: a modell komplexitást büntetik, elkerülve így a túl komplex modellek alkalmazását.
Számos olyan kritériumot definiáltak, melyek ezt az elvet követik. Ezek között a legfontosabbak a különböző információs kritériumok, elsősorban az Akaike információs kritérium (Akaike information criterion, AIC) [Aka74], valamint a végső előrejelzési hiba (final prediction error, FPE) [Aka69] vagy a minimális leíró hossz (minimum description length, MDL) [Ris78]. Ezeket a kritériumokat elsődlegesen lineáris rendszerek komplexitásának meghatározására dolgozták ki, de korlátozottan alkalmazták őket nemlineáris dinamikus rendszereknél, így dinamikus neuronhálóknál is (ld. pl. [Nør00]. Ezen kritériumok közös jellemzője, hogy két tagból állnak: a kritérium első tagja a tanítópontokbeli hibát veszi számba (tapasztalati hiba), míg a második tag egy büntető tag, melynek értéke annál nagyobb, minél nagyobb komplexitású a modell. Az általános forma:
Vegyük észre, hogy ez az általános forma rokon a 2. fejezetben bemutatott strukturális kockázat minimalizálási (SRM) elvnél alkalmazott általános formával. Lényeges különbség azonban, hogy míg az SRM elvhez kapcsolódó felső korlátok (pl. (2.31) összefüggés) a komplexitás mértékeként a VC-dimenziót használják, addig itt a komplexitást a modellstruktúra szabad paramétereinek a száma fejezi ki.
Az előbbi kritériumok alkalmazása olyan modell kialakítására próbál kényszeríteni, ahol nemcsak a hibát, hanem a komplexitást is minimalizáljuk. Így valójában itt is az ún. Ockham borotvája (Ockham’s razor) elvet alkalmazzuk, amely azt mondja ki, hogy két azonos minőségű megoldás közül mindig az egyszerűbbet válasszuk.[5]
Ezeken a kritériumokon kívül kidolgoztak más eljárásokat is a modell-fokszám meghatározására. Dinamikus neurális hálók fokszám-meghatározására született a Lipschitz indexenalapuló heurisztikus eljárás [He93], amelyet a következőkben foglalunk össze. A fokszám meghatározás valójában azt adja meg, hogy a regresszorvektorban (ld. (8.3)-(8.7) összefüggések) hány komponens szerepel és melyek ezek a komponensek. Egy nemlineáris dinamikus rendszermodell (8.1) szerint a regresszorvektor (nemlineáris) függvénye. Ebben a felfogásban a fokszám azt adja meg, hogy ennek a függvénynek hány bemeneti változója van. A Lipschitz indexen alapuló eljárás a bemeneti változók megfelelő számát és a megfelelő bemeneti változókat próbálja meghatározni.
Az eljárás azon alapul, hogy feltételezhetjük a nemlineáris dinamikus rendszer által megvalósított leképezés folytonosságát. A módszer érdekessége és a gyakorlati alkalmazás szempontjából az előnye, hogy kizárólag a tanító adatokból dolgozik.
A módszer bemutatásához induljunk ki abból, hogy adott egy nemlineáris bemeneti-kimeneti leképezés:
, (8.65)
amely egy folytonos, sima, többváltozós függvény valamilyen értelmezési tartományon, és ahol az változók a függvény bemeneti változói. Az f függvény az független változók mindegyikétől, de csak ezektől a független változóktól függ. A megfelelő számú bemeneti változó meghatározása a következő, Lipschitz indexnek nevezett mennyiség alapján lehetséges:
(8.66)
ahol a
(8.67)
Lipschitz hányadosok közül a k-adik legnagyobb érték, N a bemeneti változók száma (a regresszorvektor dimenziója), p pedig egy alkalmasan megválasztott pozitív szám, rendszerint p = 0,01P ~ 0,02P. (P a szokásos jelölésnek megfelelően a tanítópontok száma).
Tételezzük föl, hogy az függvény bemeneti változók szerinti deriváltjai korlátosak, vagyis
, (8.68)
ahol M egy véges pozitív érték.
Ha a függvény folytonos, a Lipschitz hányados korlátos kell legyen, vagyis
(8.69)
bármely i,j adatpárra. A sok adatpár közül azokat vizsgáljuk, ahol a Lipschitz hányados értéke nagy.
Határozzuk meg a Lipschitz hányados felső korlátját. A függvénykapcsolat érzékenységi vizsgálata alapján a kimenet megváltozása a bemenetek megváltozásai alapján az alábbi formában írható fel:
(8.70)
ahol az függvény xl szerinti parciális deriváltja, l=1, …, N és . Felhasználva a deriváltra vonatkozó (8.68) felső korlátot és a Schwarz egyenlőtlenséget, továbbá, ha a bemeneti térben az euklideszi normát használjuk, a Lipschitz hányadosra az alábbi felső korlátot kapjuk:
(8.71)
Az függvény rekonstrukcióját akarjuk mintapontok alapján megkapni. Ha a függvény valóban kielégíti a (8.68) összefüggést, és az összes bemeneti változó szerepel az függvény rekonstrukciójában, akkor az összes mintapárra számított Lipschitz hányadosra érvényes kell legyen a (8.71) felső korlát.
Tételezzük most fel, hogy valamelyik bemeneti változó, pl. xN hiányzik a függvény rekonstrukciójánál, vagyis a mintapontoknál az xN komponens hiányzik. Ekkor két bemeneti pont közötti távolságra adódik, miközben a megfelelő kimenet-megváltozás változatlan marad, vagyis a Lipschitz hányados
(8.72)
lesz. Ha xN független a többi bemeneti változótól, extrém nagy, sőt végtelen értéket is felvehet. Ilyen eset állhat elő, ha , és tetszőlegesen kicsi, de nem nulla. Ha xN nem teljesen független az bemeneti változóktól (ilyen helyzet lehet pl. ha egy jel késleltetett értékei), akkor sokkal nagyobb lesz, mintha a bemeneti változók között xN is szerepelne. Ebből a vizsgálatból az következik, hogy ha egy szükséges bementi változó hiányzik a bemeneti vektorból, a Lipschitz hányados nagyon nagy értéket is felvehet. Minél több változó hiányzik, annál nagyobb lehet a Lipschitz hányados. Ha ez a helyzet áll elő, semmilyen nemlineáris approximációs eszköz sem lesz képes megtanulni a leképezést kielégítő minőségben.
Ha a bemenetek közé egy redundáns változót, pl. xN+1-et is bevesszük a Lipschitz hányadosra a következő adódik:
. (8.73)
csak kismértékben lehet kisebb, mint , vagyis . Ha további redundáns változók kerülnek a bemeneti vektorba a Lipschitz hányadosok jelentősen nem fognak változni. Egy bemeneti változó az függvénykapcsolat szempontjából akkor redundáns, ha ettől a változótól – jelen esetben xN+1-től – a függvényérték, y nem függ.
Fentiek alapján látható, hogy a Lipschitz index tulajdonsága, hogy ha N a bemeneti változók megfelelő száma, akkor közel azonos -nel, de jóval kisebb, mint . Továbbá is sokkal kisebb, mint , miközben közel azonos -gyel és így tovább. Ebből adódóan, ha felrajzoljuk az Lipschitz index alakulását N függvényében, azt figyelhetjük meg, hogy adott N0 értéktől kezdve N-től egyre kevésbé fog függni, viszont N0-nál kisebb számú bemeneti változó esetén N növelésével meredeken csökken. Ez az N0 érték lesz a bemeneti változók megfelelő száma.
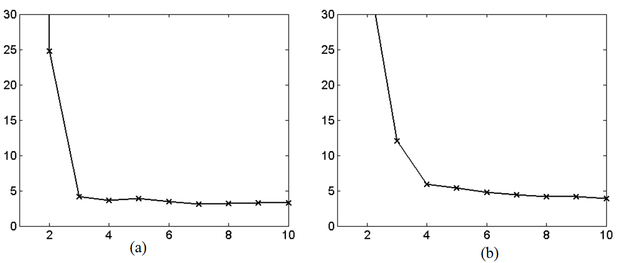
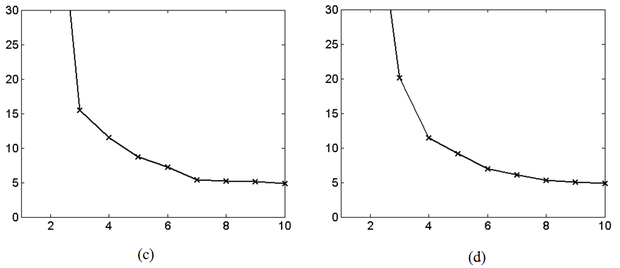
A 8.17 (a) ábra jól mutatja, hogy N0=3-nál a Lipschitz index minimumot vesz fel. Az ábra azt az ideális helyzetet tükrözi, amikor a megfigyeléseink zajmentesek. A görbe közel hasonlóan alakul akkor is, ha a mintapontok kismértékben zajosak (8.17 (b) ábra). Ha a zajszint növekszik a görbén látható határozott töréspont egyre inkább elmosódik. Erre mutat példát a 8.17 (d) ábra.
A (8.66) összefüggésből látható, hogy a Lipschitz index a Lipschitz hányados-sorozat -nel szorzott értékeinek mértani középértéke. A mértani közép alkalmazásának oka, hogy így az index alakulása kevésbé érzékeny a tanító adatokat terhelő mérési zajra.
Ha a fenti eredményeket a fokszámmeghatározásra alkalmazzuk, akkor valójában azt határozzuk meg, hogy a regresszorvektorban hány komponensnek kell szerepelnie (és melyek ezek a komponensek). A bemeneti komponensek most a dinamikus modellstruktúra osztály függvényében a rendszer régebbi bemeneti (NFIR struktúra), régebbi bemenetei és a régebbi rendszerkimenetek (NARX struktúra), stb. lesznek.
NFIR modellstruktúra esetén az eljárás a következő: Az Lipschitz indexet több különböző modell-fokszám érték mellett kell meghatározni, ahol N jelöli az előrecsatoló ág fokszámát. N=1-gyel kezdve csak x(k-1)-et vesszük be a regresszorvektorba. Ezzel számíthatjuk ki értékét. N=2 esetén x(k-1) mellett a regresszorvektor már x(k-2)-t is tartalmazza, így számítható . Ha közel azonos -gyel, x(k-2)-re nincs szükség. Ezzel szemben, ha jelentősen kisebb, mint , x(k-2) része marad a regresszorvektornak és a fokszámnövelést innen folytatjuk x(k-3)-mal. Ezt a stratégiát folytatva lépésről-lépésre növeljük az előrecsatoló ág késleltetéseinek számát, amíg a megfelelő fokszámot el nem érjük.
A Lipschitz index nemcsak NFIResetben, hanem NARXhálózatoknál is alkalmazható, ahol két fokszámérték meghatározása a cél. A NARX modelleknél az előrecsatoló ágban lévő késleltetések száma mellett a visszacsatoló ág késleltetett értékeinek számát is meg kell határozni.
NARX modell estén a következő stratégia szerint járhatunk el. Az Lipschitz indexet több különböző modell-fokszám érték mellett kell meghatározni, ahol R az eredő fokszám és ezen belül M jelenti a visszacsatoló ág, N pedig az előrecsatoló ág fokszámát. Ha R=1, akkor csak -et vesszük be a regresszorvektorba. Ezzel számíthatjuk ki értékét. R=2 esetén d(k-1) mellett már x(k-1)-et is szerepeltetjük a regresszorvektorban, így számítható . R=3 mellett d(k-2) is felhasználásra kerül, vagyis számítható. Ha azonban közel azonos -gyel, a visszacsatoló ágban nincs szükség két késleltetésre. Helyette az R=3-hoz a bemeneti ágban kell egy újabb késleltetett értéket, x(k-2)-t felhasználni és -t kell meghatározni. Ezzel szemben, ha jelentősen kisebb, mint , d(k-2) része marad a regresszorvektornak és a fokszámnövelést innen folytatjuk x(k-2)-vel. Így juthatunk el -höz, amit ismét össze kell hasonlítanunk -gyel. A továbblépés az összehasonlítás eredményétől függően vagy az (M,N)=(2,2) struktúra megtartását jelenti, vagy vissza kell térni az (M,N)=(2,1) felépítéshez, ahonnan a továbblépés ismét M növelésével az index meghatározásához vezet. Ezt a stratégiát folytatva lépésről-lépésre növeljük a visszacsatoló és az előrecsatoló ág késleltetéseinek számát, amíg a megfelelő fokszámot el nem érjük.
A Lipschitz index alapú eljárás előnye, hogy közvetlenül a mintapontokból dolgozik, anélkül, hogy különböző komplexitású modellek előzetes megépítésére szükség lenne. Hátránya a viszonylag nagyfokú zajérzékenység.
8.2 példa
Példaként határozzuk meg a Mackey-Glass kaotikus folyamatmodellezésénél a modell-fokszámot. A Mackey-Glass kaotikus folyamatot a
(8.74)
differenciálegyenlet írja le. (A felhasznált idősort a differenciálegyenletből τ=17 mellett negyedrendű Runge-Kutta integrálással és (6:1)-es alulmintavételezéssel kaphatjuk. Az az így kapott idősort gyakran alkalmazzák különböző dinamikus modellezési megközelítések vizsgálatánál mintapéldaként, mint benchmark feladatot.) A Mackey-Glass folyamatból kapott idősor egy olyan kaotikus idősort definiál, ahol a folyamat korábbi értékei alapján határozható meg egy későbbi érték.
(8.75)
A folyamat modellezésére tehát egy olyan visszacsatolt rendszer lehet alkalmas, ahol külső gerjesztés nincs. NARXmodellt alkalmazva a folyamat mintavételi értékei lesznek a kívánt d(k) válaszok, vagyis a regresszorvektor (8.75) alakú lesz és a modell-fokszám meghatározása M értékének meghatározását jelenti. P=1000 mintapont alapján, továbbá, ha a Lipschitz index (8.66) összefüggésében p=10, a 8.17 ábrán látható eredményt kapjuk. Az ábra jól mutatja, hogy a zaj növelése milyen mértékben teszi bizonytalanná a Lipschitz index alkalmazását a fokszám meghatározására. Az ábrán bemutatott zajos esetekben a mintapontokat egyre nagyobb szórású additív Gauss zaj terheli.
A fenti eljárásokon túl a gyakorlatban számos további módszer alkalmazható a megfelelő modellkomplexitás meghatározására. A keresztkiértékelés (cross validation) szerepét a statikus neuronhálók minősítésénél már említettük. A módszer dinamikus hálóknál szintén alkalmazható, amikor a létrehozott modellt olyan mintákkal teszteljük, melyeket a modell kialakításánál nem használtunk. A valóságos, megfigyelt adatok és a modell kimenete közötti különbség − a maradék hiba − vizsgálata alapján értékelhető a modell minősége. A keresztkiértékelés eredménye tehát nem közvetlenül a fokszám megfelelő megválasztására utal, hanem a teljes megoldást minősíti, de a minősítés eredményét felhasználva meghatározható a megfelelő modell-fokszám is.
A maradék hiba vizsgálata (residual test) alapján eldönthető, hogy a modell kellően pontosan leírja-e a modellezendő rendszert. A modell akkor tekinthető megfelelőnek, ha az
(8.76)
maradék hiba „struktúramentes”, semmiféle „mintázatot” nem mutat, sem a bemenettel sem a kimenettel nem korrelált.
Precízebben megfogalmazva, az hibaminta sorozat
-
nulla középértékű, diszkrét fehér zaj folyamat,
-
Gauss eloszlású folyamat,
-
a hibasorozat elemei és az előző bemeneti értékek korrelálatlanok:
.
A maradék hiba vizsgálatára szolgál az autókorrelációs és a keresztkorrelációs teszt, melynek során a maradék hiba autókorrelációs illetve a hibának és a bemenetnek a keresztkorrelációs függvényét becsüljük.
Az autókorrelációs függvényt véges számú mintapont alapján az alábbi módon becsülhetjük:
(8.77)
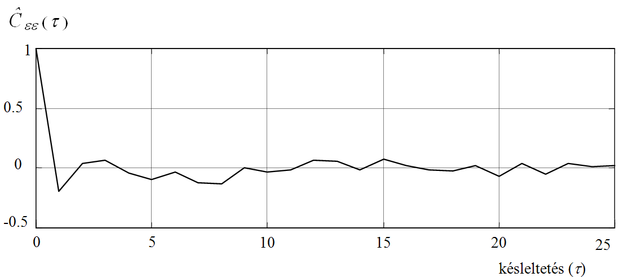
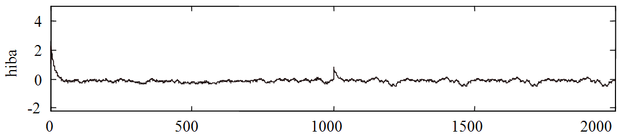
Minél inkább fehérzaj a maradék hiba (vagyis minél inkább „struktúramentes”), annál inkább az impulzusfüggvényhöz tart az autókorrelációs függvény. A 8.18 ábra egy tipikus példát mutat a maradék hiba autókorrelációs függvényére.
A keresztkorreláció a maradék hiba és a bemenet közötti kapcsolat vizsgálatára szolgál. A keresztkorrelációs függvény az alábbi összefüggés szerint becsülhető:
(8.78)
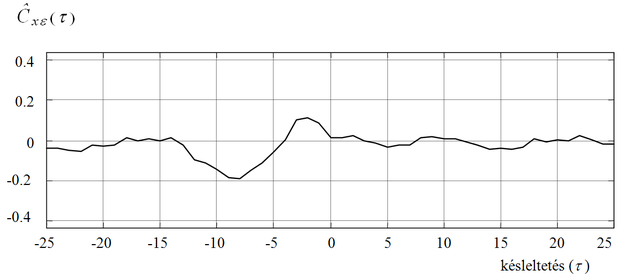
Megfelelő pontosságú modell esetén a maradék hiba és a bemenet korrelálatlan, vagyis a keresztkorrelációs függvény értéke közel nulla bármilyen τ késleltetés mellett is. Egy tipikus keresztkorrelációs kapcsolatot mutat a 8.19 ábra.
A kísérlettervezés célja olyan feltételeket teremteni, melyek mellett kellő számú és a működést kellő mértékben reprezentáló minta begyűjtése lehetséges a modellezendő rendszerről. A feladatok egy jelentős részében a kísérlettervező kezében van, hogy a modellezendő rendszer milyen gerjesztő jelet kapjon, vagyis a bemeneti jelet a kísérlettervező határozhatja meg. Más feladatoknál a tanítás céljára történő adatok gyűjtésénél a bemenet megtervezésére nincs lehetőség, azt a modellezendő rendszer normál működése megszabja.
A megfelelő gerjesztőjel, az ún. perzisztens gerjesztés (persistent excitation) megtervezése önálló tudomány. A gerjesztőjel megválasztásánál, még lineáris rendszereknél is sokféle szempont figyelembevétele szükséges [Nar89] [Lju99], [Pin01]. A gerjesztőjel megtervezésekor kell döntenünk, hogy a standard vizsgálójelek (impulzus, egységugrás, fehérzaj, multiszínusz, bináris álvéletlen jel, stb.) közül melyiket vagy melyeket alkalmazzuk. Nemlineáris rendszereknél a helyzet még bonyolultabb, hiszen nemlineáris rendszereknél az átvitel akár a jelszintnek is a függvénye. Rosszul megválasztott jelszintekkel létrehozott tanító készlet alapján konstruált dinamikus neurális modell más jelszinteknél jelentős hibával írja le a rendszer működését. Ezt illusztrálja a következő példa.
8.3 példa
Legyen a modellezendő rendszer a következő:
(8.79)
ahol
(8.80)
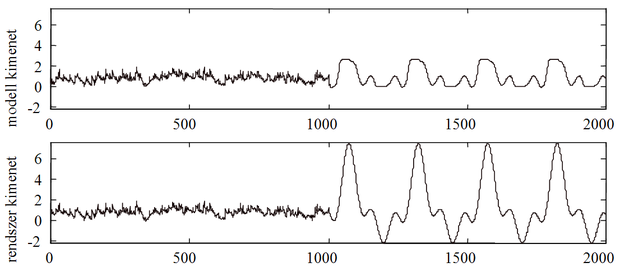
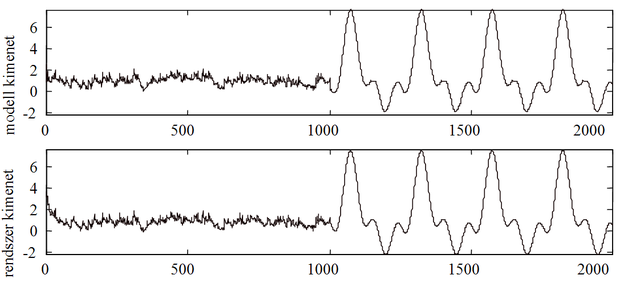
A feladat NARXvagy NOEmodellstruktúrával oldható meg. A tanításnál alkalmazható a NARX struktúra, míg a tesztelésnél már a modell saját kimenetét csatoljuk vissza, vagyis a tesztelés NOE architektúra mellett történik. A neurális modell létrehozásához egyenletes eloszlású véletlen bemenőjelet használva a 8.20 és a 8.21 ábrák a bemenő jelszint helyes megválasztásának fontosságára hívják fel a figyelmet.
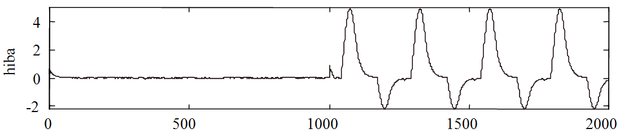
A két ábra-együttes a megtanított háló válaszát, a kívánt választ (a rendszer kimenete) és a maradék hibát mutatja olyan teszt mintasorozatra, ahol a tesztminta első 1000 pontja kis amplitúdójú véletlen jel, a második 1000 minta nagyobb amplitúdójú szinuszos jel volt. A 8.20 ábra esetében a dinamikus hálót kis amplitúdójú, a [-1,1] intervallumban egyenletes eloszlású véletlen bemenőjel mellett létrehozott tanítómintákkal tanítottuk, míg a 8.21 ábrán a gerjesztő véletlen jel nagyobb amplitúdójú volt (egyenletes eloszlású jel a [-2,2] intervallumban). A teszt válaszokból jól látható, hogy az első esetben a háló csak kis amplitúdójú teszt bemenőjel mellett adott megfelelően jó választ, míg a második esetben a válasz a teszt mindkét részén, mind a kisszintű, mind a nagyobb szintű teszt bemenőjel mellett megfelelő.
A megfelelő modellstruktúra és tanítókészlet megválasztását követően kerülhet sor a dinamikus háló paramétereinek meghatározására, a paraméterek becslésére − ami a háló tanítását jelenti −, majd ezt követi az eredmény kiértékelésére. Ezeknél a lépéseknél egyrészt az egyes dinamikus neuronháló architektúráknál bemutatott tanító eljárások általános és speciális szempontjait, illetve a hálók tesztelésével kapcsolatos általános megállapításokat és a maradék hiba elemzésére szolgáló eljárásokat kell figyelembe venni.
A fentiekből látható, hogy a tanítókészlet nemcsak a tanítási folyamatot befolyásolja, hanem a modellstruktúra kialakításánál is szerepe van, továbbá meghatározza azt is, hogy mi lesz a modell érvényességi tartománya. Ez is azt mutatja, hogy a modellezési folyamat egyes lépései szorosan összefüggenek egymással és a megfelelő modell kialakítása csak visszalépéseket is tartalmazó iteratív folyamat eredménye lehet.
Egyes feladatoknál a rendszeridentifikáció elsődleges célja egy vizsgált rendszer modelljének a létrehozása, más esetekben az identifikáció egy összetettebb feladat részeként jelenik meg. Az első esetre példaként hozható szinte bármely mérési feladat, mivel minden mérés a rendszer valamely modell-paraméterének a meghatározását (becslését) jelenti. Az identifikáció, mint részfeladat leggyakrabban szabályozási feladatokban jelentkezik. Ekkor a rendszer modelljére pl. a szabályozó algoritmus paramétereinek meghatározásához, általánosabban a szabályozó megtervezéséhez van szükség. (A BPTT eljárásnál bemutatott 8.1 példa is illusztrálja ezt.)
A vezérlési alkalmazások célja olyan gerjesztőjel előállítása valamely rendszer meghajtására, hogy annak kimeneti jele valamilyen kritérium alapján a lehető legjobban közelítse a specifikált kimeneti jelet. (Lehet kritérium a jó követés, de lehet pl. a minimális túllövés is.) A szabályozáselmélet irodalma rendkívül sokféle – az alkalmazások nagyon különböző követelményeit kielégítő – módszert ismer.
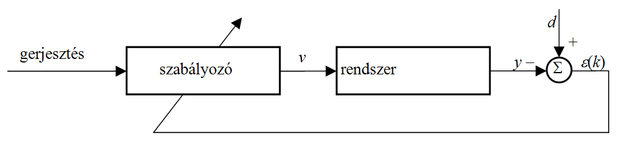
A hagyományos adaptív szabályozási módszerek blokksémája a 8.22 ábrán látható. Ezek egy állítható paraméterekkel is rendelkező szabályozót, valamint ezen paramétereket állító adaptációs algoritmust tartalmaznak. Az algoritmus a kimeneti hiba, valamint a rendszer be- és kimenete (vagy ezek egy része) alapján állítja be a vezérlő paramétereit.
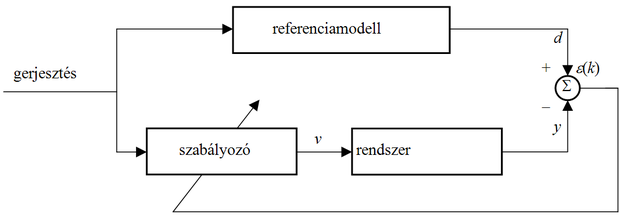
A gyakorlatban igen gyakran találkozunk azzal az igénnyel, hogy a szabályozandó berendezést – a szakaszt – úgy gerjesszük, hogy a szabályozó-szakasz együttes a zavaró, változó környezeti hatások ellenére is, egy specifikált referenciamodellhez hasonlóan viselkedjen (pl. a repülőgép úgy reagáljon a kormánymozdulatokra, ahogy azt a pilóták "szeretik"). Az ilyen környezetben használható szabályozásokat nevezzük modell alapú adaptív szabályozásnak (Model Reference Adaptive Control, MRAC).
A neurális hálózatok alkalmazása modell alapú adaptív szabályozásra sokmindenben hasonlít az identifikációra. Ha sikerül ugyanis úgy adaptálnunk a vezérlőnek használt neurális hálózat paramétereit, hogy az a szakasszal együtt úgy viselkedjen, mint a referenciamodell, akkor megoldottuk a feladatot. Ez pedig tulajdonképpen azt jelenti, hogy a vezérlőből és a szakaszból álló modellel identifikáltuk a referenciamodellt. A különbség abban áll, hogy – az identifikációs feladattól eltérően – ebben az esetben nem a neurális hálózat, hanem a szakasz kimenetén képződik az adaptációhoz használható hiba. Ezt a hibát pedig közvetlenül nem lehet felhasználni a hálózat paramétereinek meghatározásához.
Az MRAC irodalmából az derül ki, hogy a vezérlő paramétereinek közvetlen adaptálására jelenleg még hagyományos szabályozó, sőt lineáris szakasz esetén sincs módszer. (A vezérlő paramétereinek ilyen, azaz közvetlen állítását a szakirodalom közvetlen szabályozás (direct control) néven említi. Közvetlen szabályozást azért nem tudunk megvalósítani, mert a valódi, fizikai rendszeren nem tudunk gradienst visszaterjeszteni, ami pl. a hibavisszaterjesztéses algoritmus alkalmazásához szükséges lenne.)
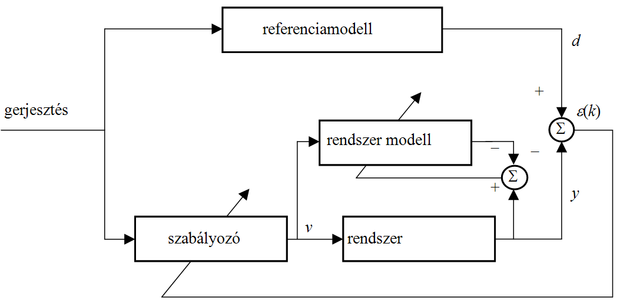
Jelenlegi tudásunk alapján a vezérlő paramétereit az ún. közvetett szabályozás (indirect control) módszerrel tudjuk állítani. Ennek lényege az, hogy a szakasszal párhuzamosan kapcsolunk egy identifikáló egységet, amely képes a szakaszt megfelelő pontossággal modellezni, ugyanakkor a vezérlő adaptálásához szükséges gradiens visszaterjesztésére is lehetőséget nyújt. Ha a gradiens információ már rendelkezésünkre áll, akkor megfelelő dinamikus tanító algoritmussal a vezérlőnek használt hálózat paraméterei meghatározhatók.
A következőkben – részben a fentiek illusztrálására – két konkrét alkalmazási területet, illetve néhány mintapéldát említünk meg röviden. A valóságos gyakorlati alkalmazások részletes elemzése meghaladja a könyv lehetőségeit. Egy valóságos „éles” feladat megoldása a megoldandó problémák részletes elemzését is igényli, így minden feladat valójában egyedi megfontolásokat igényel. A megoldások egyedi jellege ellenére azonban a különböző feladatokból bizonyos általános tapasztalatok is levonhatók. A gyakorlati feladatok megoldásánál felmerülő legfontosabb általános kérdésekkel és tapasztalatokkal a 13. fejezet foglalkozik.
Neurális hálózatok alkalmazására a robotika egy igazi „állatorvosi ló”. Alkalmazásuk már csak azért is felvetődik e területen, mert minden robot erősen nemlineáris rendszer. Mivel a felmerülő problémák igen sokfélék, az új módszerek kipróbálására sok lehetőség adódik. Néhány a felvetődő területek közül: pályatervezés, pályakövetés, szenzor információk feldolgozása, autonóm eszközök intelligens irányítása, egyes stabilitási problémák, stb. Az alkalmazások egy részében a neurális hálózat szerepelhet egy korábban már ismert algoritmus, módszer realizációjaként is (pl. sebességi megfontolások miatt). Példaként álljon itt néhány konkrét robotikai alkalmazás.
Isabelle Rivals és munkatársai egy olyan rendszert fejlesztettek ki, mely egy négykerék meghajtású Mercedes terepjáró automatikus irányítását látta el [Riv94]. A neurális megoldás szabályozta a gázadagolást, a fékezést, a kormánybeállító szervó rendszert annak érdekében, hogy az autó egy előírt pályán, előírt sebesség-profillal mozogjon változó környezeti feltételek (pl. széllökések, csúszós és különböző meredekségű útszakaszok) mellett.
Simon Yang és Max Meng egy neurális robot-mozgás tervező rendszert ismertet [Yan00]. A feladat egy mobilis robot mozgásának irányítása ismeretlen, akadályokat is tartalmazó környezetben.
Frank Lewis neuronhálót alkalmaz robot manipulátor irányítására [Lew96]. A feladatok között egyebek mellett a manipulátor pozíciója és a manipulátor által kifejtett erő szabályozása szerepel.
További sikeres alkalmazási példák a bőséges irodalomban (pl. [Bek93], [Pra96], [Sma06]) találhatók.
Számos gyakorlati feladat megoldásánál jelentkezik igény valamiféle előrejelzésre, jóslásra [Che04] (egy nagy haszonnal kecsegtető, bár igen nehéz terület pl. a valutaárfolyamok, tőzsdei árfolyamok előrejelzése). Az előrejelzési feladatok megoldása is alapvetően a neuronhálók modellező képességén alapul, hiszen minden jóslási feladat lényege az, hogy egy rendszer jövőbeli viselkedésének előrejelzése a múltbeli viselkedésének modellezése alapján, a rendszer eddigi "történetének" felhasználásával lehetséges.
A jóslási feladat sok esetben egy idősor alakulásának előrejelzését jelenti. Valójában az idősor előrejelzés is rendszermodellezési feladat; az idősor rendelkezésre álló része alapján próbáljuk annak a rendszernek a viselkedését minél pontosabban leírni, amely az idősor egyes értékeit előállítja. A rendszermodell birtokában az idősor folytatása, az előrejelzés már könnyen megoldható.
Idősor előrejelzési feladatokat „hagyományos” megközelítés alkalmazásával, fejlett statisztikai eljárások felhasználásával is megoldhatunk sikeresen. A neuronháló alapú megoldások eredményei azonban arra engednek következtetni, hogy ilyen jóslási feladatoknál a neurális hálózatok alkalmazása jobb eredményre vezethet, vagy megfelelő eredményt könnyebben, kevesebb erőfeszítéssel nyerhetünk. Tulajdonképpen a jóslási folyamat során felépül egy jelmodell, amely megpróbálja leírni a vizsgált jelsorozatot. Ez a jelmodell neurális hálózatok alkalmazása során „automatikusan”, a hálózaton belül épül fel.
Az alábbiakban két tesztfeladatot mutatunk be.
A Mackey-Glass kaotikus folyamatot, mint gyakori benchmark problémát a modell-fokszám becslési eljárásoknál említettük (ld. 8.2 példa). A kaotikus folyamatok tesztfeladatként való felhasználását az indokolja, hogy ezen folyamatok jövőbeni alakulásának előrejelzése különösen nehéz, hosszútávú előrejelzésük pedig gyakorlatilag lehetetlen.
Az előrejelzési feladatot itt is úgy fogalmaztuk meg, hogy a folyamatból származtatott diszkrét idősor pillanatnyi és régebbi mintái alapján a következő időponthoz tartozó érték előrejelzésére van szükség, tehát egylépéses előrejelzési feladattal van dolgunk. A megoldás NARXmodell-osztály mellett, a 8.2 példában meghatározott modell-fokszám alkalmazásával, Gauss kernellel dolgozó LS-SVM hálózattal (σ=2,6, C=1 hiperparaméterek mellett) történt. A tanítókészlet 500 mintaszekvenciából állt. Az LS-SVM előrejelzésének eredménye a 8.25 ábrán látható. Az ábra felső részén az eredeti idősor és az előrejelzés szerepel; a vékonyabb folytonos vonal az eredeti folyamat alakulását, a vastagabb a háló előrejelzését mutatja. Látható, hogy az előrejelzés és a folyamat valódi mintái az ábra szerinti felbontásban szinte egymásra kerülnek. A két görbe különbsége, az előrejelzési hiba látható az ábra alsó részén. Ezzel a megoldással gyakorlatilag ekvivalens eredményt érhetünk el LS2-SVM-mel is. Ennek a megoldásnak az előnye ugyanakkor, hogy LS2-SVM-mel ritka megoldást érhetünk el lényegében a minőség romlása nélkül: az 500 mintaszekvenciából 55 szupport vektor elegendőnek bizonyult.
1991 augusztusában az amerikai Santa Fe Institute írt ki egy nyilvános versenyt, amely során hat mintasorozatnak kellett megjósolni a folytatását. A szervezők egymástól teljesen eltérő jellegű feladatokat adtak ki, és semmiféle megkötést nem tettek az alkalmazható módszerre vonatkozóan. Maguk a szervezők is meglepődtek azon az eredményen, hogy a neurális hálózatokat alkalmazó megoldások mindegyik jel esetén jobbnak bizonyultak az egyéb – igen széles skálán mozgó – megoldásoknál [Wei94].
A közzétett jelsorozatok az alábbiak voltak:
-
egy fizikai kísérlet (egy laboratóriumi NH3 lézer),
-
számítógéppel generált véletlen sorozat,
-
svájci frank − amerikai dollár keresztárfolyamának változása,
-
asztrofizikai adatok egy változó törpecsillagról,
-
fiziológiás adatok,
-
mintavett jelsorozat J. S. Bach: "A fúga művészete" c. művének, utolsó, befejezetlen darabjából.
Az adatok – mint látszik – tényleg eléggé eltérőek, még jellegüket tekintve is. Azonban éppen ez a sokszínűség az, amely a neurális hálózatok alkalmazhatóságát látszik igazolni jóslási feladatok során.
A Santa Fe versenyt követően jónéhány hasonló versenyt írtak, ki. Ezek a versenyek az utóbbi években a neuronhálókkal foglalkozó évenként megrendezésre kerülő legrangosabb nemzetközi konferenciához, az International Joint Conference on Neural Network (IJCNN)-höz kapcsolódnak.
A gyakorlatban előforduló valódi jóslási feladatok megoldása során szinte mindig rendelkezésre áll bizonyos a priori információ a vizsgált jelenséget illetően. Ez az információ beépíthető a modellekbe a megoldás során, jelentősen javítva a jóslás megbízhatóságát. Az a priori információ beépítése neurális hálózatokba (pl. a súlyok kezdeti inicializálása, stb. által) még nem teljesen megoldott, így ebből a szempontból még sok kutatásra van szükség. Mivel a Santa Fe verseny során a rendezők a jelekről semmilyen a priori információt nem tettek közzé, valószínűleg a hagyományos módszerek „nem tudták a legjobb formájukat hozni”.
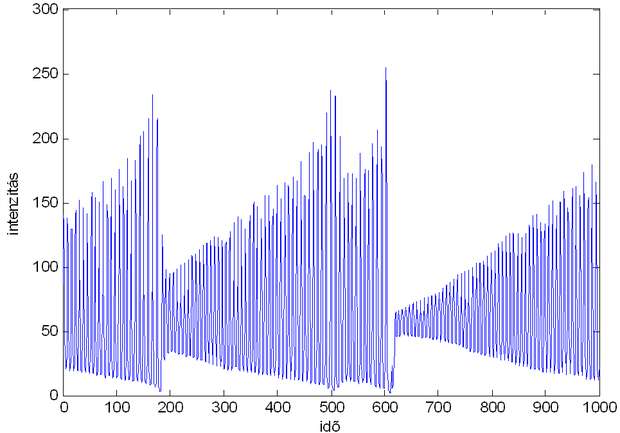
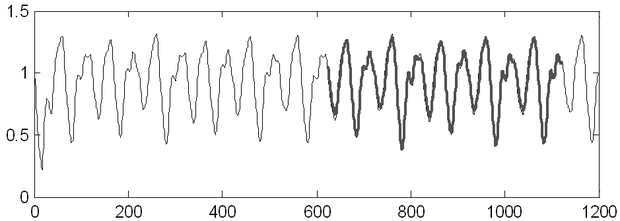
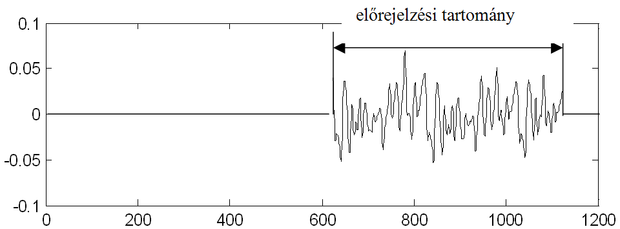
A következőkben az első jelsorozat, az NH3 lézer intenzitás előrejelzését megoldó neurális megoldást, mint ennek a feladatnak a győztesét mutatjuk be [Wan93]. A feladat nehézségét az jelenti, hogy a lézerjel intenzitása időben nem állandó, hanem folyamatosan és gyorsan pulzál a szélső értékek között, ráadásul a folyamat kaotikus jellegű. A közreadott kiinduló jelszegmens, mint időfüggvény a 8.26 ábrán látható.
A konkrét feladatban egy 1000 hosszú adatsor állt rendelkezésre, és ebből kellett megjósolni a lézerjel intenzitását a következő 100 időpillanatban. A verseny ideje alatt az idősorról semmiféle háttér információt nem tettek közzé. A versenyzőknek a priori ismeretek bevetése nélkül, puszta számok alapján kellett előrejelzőt építeni. (Természetesen ez a tiszta „fekete doboz” megközelítés tényleges gyakorlati feladatok megoldása esetén nem célszerű. Viszont előrejelző algoritmusok összehasonlítására kiválóan alkalmas, mivel így maguk az algoritmusok kerülnek összevetésre, nem pedig az a priori tudás beépítésének módjai.)
A versenyben hibakritériumként a tényleges idősor empirikus szórásnégyzetével normalizált átlagos négyzetes hibát használták. Az alkalmazott megoldás az előző feladat megoldásához hasonlóan egylépéses predikcióra vezette vissza a középtávú előrejelzési feladatot. Ez azt jelenti, hogy a háló konstrukciójánál NARXmodellosztályt alkalmaztak, melyet a tanítás után mint NOEmodellt működtettek. Az idősor természete és a megcélzandó hibakritérium alapján nyilvánvaló volt, hogy a nagy intenzitás-visszaesések (lásd a 200-as, az 510-es és a 600-as pontok környékét) megjóslása kulcsfontosságú. Ez érdekes jelleget ad a feladatnak, mivel ilyen mintázatból a rendelkezésre álló idősorban mindössze 3 található.
A versenygyőztes FIR-MLP hálózat a bemeneti és a kimeneti neuronon kívül 2 rejtett réteget tartalmazott, mindkettőben 12-12 neuronnal. Az első rejtett réteg bemenetei 25-öd fokú, míg a további két réteg bemenetei 5-ödfokú szűrők voltak. Ezeknek a paramétereknek a beállítása kereszt kiértékeléssel történt. Ilyen felépítés mellett a FIR-MLP hálózatnak összesen 1105 szabad paramétere volt, ami a tanító készlet méretéhez képest igen nagy szám. Erre a szerzők szerint azért volt szükség, mert a kísérletek azt mutatták, hogy kisebb hálózattal a hirtelen nagy visszaesések helyei nem jósolhatók meg elég pontosan. A sok szabad paraméter azt is eredményezi, hogy a távoli időpillanatokra adott becslések varianciája nagy lesz, de ez még mindig kevésbé növeli a hibát, mintha nem sikerült volna eltalálni a hirtelen intenzitás-visszaesés időpontját. Vegyük észre, hogy miközben a modell ténylegesen a NARX modellstruktúrának megfelelően épült fel, az alkalmazott háló architektúra FIR-MLP volt. A FIR-MLP azonban nem valódi bemenőjelet kapott (hiszen ilyen a feladatban nincs is), hanem a kívánt válasz, a lézerjel régebbi értékeit.
A háló kezdeti súlyait úgy állították be, hogy a súlyoknak 0 és 1 közötti véletlen értékeket adtak, majd minden neuron súlyát a bemenetszám négyzetgyökével fordítottan arányosan skálázták. A kimeneten lineáris neuront használtak, hogy a háló kimenete szélesebb értéktartományban mozoghasson. (A kimenet jövőbeli értéktartományát előre nem lehetett megbecsülni, amire normalizált kimenethez szükség lett volna.) Tanulási tényezőként 0.001-et használtak (heurisztikusan állították be így). A rendelkezésre álló idősor első 900 pontját használták tanításra, a maradék 100-on végezték a tesztelést. Egy teljes tanítás során tipikusan kb. 2000-szer haladtak végig a tanító készleten.
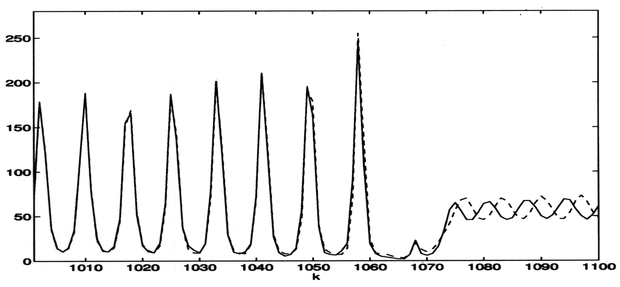
Mivel a tesztelő készlet nem tartalmazott egyetlen hirtelen intenzitás-visszaesést sem, ezért ellenőrzésképpen a hálókkal az 550-es ponttól is indítottak 100 lépéses predikciókat. Ez némileg „csalás”, de olyan kevés adat állt rendelkezésre, hogy a szerzők így döntöttek. Természetesen meg kell jegyeznünk, hogy ezeknél az ellenőrzéseknél az 550-es ponton túl a hálózat nem a tanító készlet elemeit kapta bemenetként, hanem a saját korábbi előrejelzéseit (NOE modell). A FIR-MLP-vel kapott előrejelzés eredménye a 8.27 ábrán látható.
Érdekesség, hogy a verseny után közzétették a lézer idősor 10 000 pontból álló folytatását. A kísérletek azt mutatták, hogy a versenygyőztes hálózat akkor is jó eredményeket produkált, ha nem az 1001-edik időpillanattól kezdve végezték el a 100 lépéses predikciót, miközben a hosszabbtávú előrejelzésnél a hiba drasztikusan nőtt. Ez azt jelenti, hogy a háló megtanulta a lézerjel dinamikáját, de a NOE architektúra miatt az előrejelzési hibák halmozódása miatt a soklépéses előrejelzés nem lehetséges.
A feladatot megoldották LS-SVM-mel is [Suy02a]. A Gauss kernellel felépített LS-SVM alapú NARX modell 50 régebbi minta alapján adott egylépéses előrejelzést. Az 50 elemű regresszor következménye, hogy a tanítópontok 50 elemű bemeneti vektorokból és a hozzájuk tartozó skalár kimenetekből álltak. Itt emlékeztetni szeretnénk, hogy SVM-nél a kernel trükk miatt a sokdimenziós bemeneti vektorok nem feltétlenül jelentenek hátrányt. LS-SVM-nél a megoldandó lineáris egyenletrendszer mérete nem függ a bemeneti dimenziótól. A hiperparamétereket, a Gauss kernel szélesség-paraméterét és a C regularizációs együtthatót kereszt kiértékeléssel határozták meg. Az LS-SVM-mel elért megoldás minőségét tekintve teljes mértékben egyenértékű a FIR-MLP eredményével.
Feladatok
8.1 Egy FIR-CMAC hálónál határozza meg a kimeneti réteg szűrő együtthatóinak tanítási összefüggéseit gradiens módszer alkalmazása esetén.
8.2 Konstruáljon FIR-RBF hálót, amelynek rejtett rétege megegyezik az eredeti RBF háló rejtett rétegével, a kimeneti rétegében pedig a súlyok helyett FIR szűrők találhatók. Határozza meg a rejtett réteg paramétereinek tanítási összefüggéseit, ha azokat is ellenőrzött tanítással, gradiens módszerrel kívánjuk meghatározni. (ld. még a 5.3 feladatot).
8.3 A 8.12 (a) ábra szerinti modellnél N egy többrétegű perceptron, a kimeneten lévő lineáris dinamikus rendszer átviteli függvénye pedig a következő:
Határozza meg az MLP tanítási összefüggéseit, ha dinamikus hibavisszaterjesztéses eljárást használ.
8.4 Egy 3-bemenetű, két rejtett elemű, egykimenetű MLP hálózat súlyai helyén két megcsapolásos FIR szűrőket alkalmazunk. Határozza meg a háló virtuális megfelelőjét az időbeli kiterítés módszerét alkalmazva. Hány súly található a kiterített virtuális hálóban?
8.5 Egy személyautót szeretnénk hátramenetben beparkoltatni egy járda mellett két autó közé. Konstruáljon olyan neurális kontrollert, amely a feladatot megoldja. Készítse el az autó neurális modelljét, majd a BPTT megközelítést alkalmazva hozza létre a neurális szabályozót, melynek a kocsi kormányzása a feladata. A feladatot két változatban készítse el: (1) a parkoló autók a járdára merőlegesen, (2) a járdával párhuzamosan állnak.
8.6 Az alábbi összefüggéssel megadott Mackey-Glass kaotikus idősor előrejelzésére alakítson ki dinamikus neurális rendszert:
,
ha τ =30 és a kezdeti érték . A feladat során a folyamat 500 pontját felhasználva kell a következő 6-10 pont előrejelzését megoldania. Próbálja megoldani a feladatot LS-SVM-mel. Ehhez határozza meg a modell struktúráját (modellosztály és modell-fokszám), majd konstruálja meg a kernel gépet. A megtanított hálót befagyasztva működtesse a hálót rekurzív módon a következő 100 pont jóslására. Vizsgálja meg a hiba alakulását az eredeti idősor adataihoz viszonyítva. Rajzolja fel mind az eredeti, mind a becsült idősor fázisdiagramját (az összetartozó minták kapcsolatát egy kétdimenziós ábrán).
8.7 Az alábbi logisztikai egyenletnek nevezett összefüggéssel adott a Feigenbaum kaotikus idősor:
,
Határozza meg a modell fokszámát a Lipschitz index segítségével. Vizsgálja meg a Lipschitz index alakulását, ha a mintákat additív Gauss zaj terheli.
8.8 Az előző feladat eredményeit felhasználva konstruáljon olyan dinamikus neuronhálót, amely modellezi a kaotikus folyamat viselkedését. Generáljon megfelelő számú mintát egy olyan tanítókészlethez, amelynek segítségével megtanított dinamikus neuronháló az idősor előrejelzését 20 lépésre előre meg tudja adni.
[5] Az Ockham borotvája elvet William of Ockham (vagy Occam) 14. századi angol filozófusnak tulajdonítják