A rekurzív háló időbeli kiterítése egy olyan módszer, amely lehetővé teszi, hogy egy visszacsatolt háló tanítására a hagyományos hibavisszaterjesztéses algoritmust alkalmazzuk [Rum86]. Minden visszacsatolásokat tartalmazó háló megfeleltethető egy tisztán előrecsatolt hálónak olyan módon, hogy az egyes processzáló elemek egymást követő időpillanatokbeli viselkedését egy processzáló elem-sorozattal helyettesítjük. E sorozat egyes elemei tehát ugyanannak a processzáló elemnek eltérő időpillanatokhoz tartozó állapotait reprezentálják, mintegy kiterítve a visszacsatolt hálózat működését az időben. A módszert, amely kisebb hálózatoknál jól alkalmazható, egy egyszerű példán keresztül mutatjuk be.

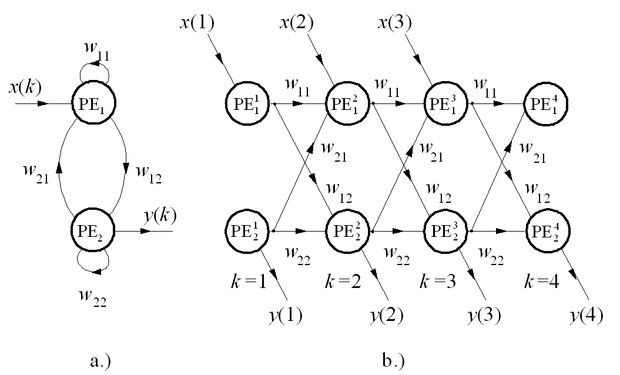
Legyen egy két processzáló elemből felépülő, teljesen visszacsatolt hálózatunk (8.6 (a) ábra). Az időbeli kiterítés eredményeképpen egy többrétegű, előrecsatolt hálót nyerünk (8.6 (b) ábra), amelynek minden egyes rétege egy-egy időpillanathoz tartozik (k=1,2,...). A háló sajátossága, hogy bár (az időablak méretétől függően) sok réteget és ennek megfelelő számú súlyt tartalmaz, a különböző rétegekhez tartozó súlyok azonos értékűek, hiszen fizikailag azonos súlyokról van szó.

Az előrecsatolt háló a standard hibavisszaterjesztéses eljárással tanítható azzal az eltéréssel, hogy minden lépésben nem módosíthatjuk a súlyokat, és a fizikai azonosság folytán a különböző rétegekbeli súlyokat sem módosíthatjuk egymástól függetlenül. Az egyes időpillanatokhoz tartozó kívánt válaszok azonban összevethetők a háló megfelelő időpillanatbeli tényleges kimenetével, így lépésenként meghatározható a hiba. A lépésenkénti hiba a kiterített hálónál rétegenkénti hibát jelent, tehát most hiba nem csak az utolsó réteg kimenetén, hanem minden réteg kimenetén megadható. A súlymódosításhoz ezeket a hibákat kell a keletkezési helyüknek megfelelő rétegtől visszaterjeszteni. Szemben azonban a normál hibavisszaterjesztéses eljárással, ahol az egyes visszaterjesztések eredményeképpen eltérő súlyok módosítását végezzük, itt ugyanazon súlyokról van szó. Ezért a súlyok módosítása az összes rétegen csak egyszerre és azonos mértékben lehetséges. A szokásos eljárás, hogy a visszaterjesztésekből származó súlymódosítás-értékeket összegezzük, és az eredménnyel módosítjuk a súlyokat: az azonos indexű súlyokat egyformán, bármely rétegben is találhatók.

Az eljárás fő hátránya a viszonylag nagy számításigény és tárolási kapacitás. Az eredeti háló-méret annyiszorosával kell ugyanis dolgoznunk, ahány időlépésig kiterítettük a hálót. Természetesen a processzáló elemek többszörözése csak a tanítási fázisban szükséges, a megtanított hálót már mint rekurzív hálót működtetjük. További hátrány, hogy a hálózat valós időben nem tanítható, az egyes súlykorrekciók mindig az időablaknak megfelelő számú lépés után végezhetők el.

8.1 példa

A következőkben a rekurzív háló időbeli kiterítésének egy klasszikus alkalmazási példáját mutatjuk be. A megoldandó feladat része annak a példasorozatnak, amelyet Bernard Widrow és munkatársai dolgoztak ki annak bemutatására, hogy különböző egyszerűbb irányítási feladatokat hogyan lehet neuronhálóval megoldani.

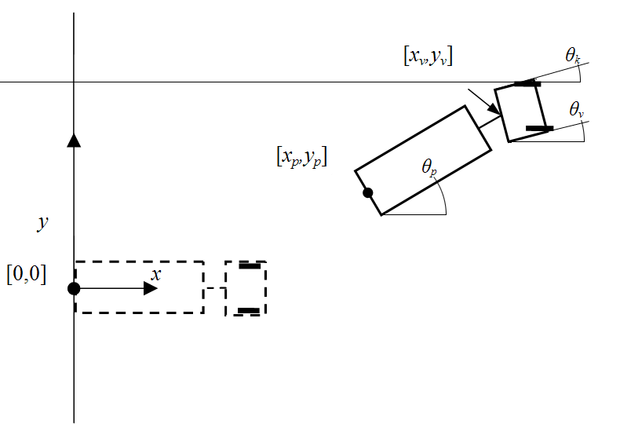
A megoldandó feladat, hogy egy pótkocsis teherautót adott kezdeti pozícióból hátramenetben adott végpozícióba juttassunk, mégpedig úgy, hogy az autó kormányát egy neurális kontroller vezérli. Az autótolatós feladat (truck backer-upper problem) a 8.7 ábrán követhető [Ngu89]. Az ábrán az [x_p,y_p] pont jelöli a pótkocsi kezdeti referencia pontját. Ebből a pontból kell kizárólag hátramenetben eljuttatni az autót az [0,0] koordinátájú pontba (az ábrán szaggatott vonallal jelzett pozíció), azt is biztosítva, hogy a végpozícióban legalább a pótkocsi álljon az x tengely irányában (a végpozícióban a θ_p szög legyen nulla).

A kontroller bemenetként a kiinduló, illetve az aktuális pozíció paramétereit kapja x=[x_p,y_p,x_v,y_vθ_p,θ_v,]^T, ahol x_v,y_v a vezetőfülke pozíciója és θ_v a vezetőfülke szöge. A kontroller feladata, hogy a kormányt a megfelelő szögbe állítsa be, vagyis θ_k értékét kell, hogy meghatározza. Feltételezzük, hogy a teherautó elemi tolató lépéseket tesz, és egy elemi lépés alatt a kormány helyzete rögzített. Egy elemi lépés tehát adott kiinduló pozícióból egy következő pozíciót eredményez. Az eredeti feladat-megfogalmazásban egy autó-pozíció jellemzésére a fenti hatelemű x vektor szolgált.

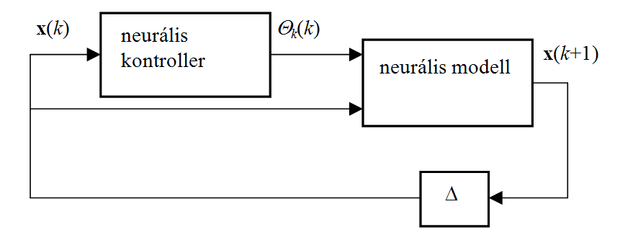
A kontroller létrehozásához előbb a kocsi modelljét kell létrehozni. Egy neurális modellhez egy nyolc-bemenetű (a pozíciót megadó hat állapotjellemző, a kormány-beállítás szöge és a szokásos eltolásérték (bias)), hat-kimenetű hálóra van szükség. A kocsi modelljének birtokában már létrehozható a kontroller-modell együttes (8.8 ábra). A kontroller feladata, hogy az x(k) pillanatnyi állapot alapján meghatározza a következő lépésben szükséges θ_k kormánybeállítást, a modell pedig a pillanatnyi állapot és a kormányszög alapján meghatározza az x(k+1) következő állapotot. A következő lépésnél ez képezi a kiinduló állapotot, tehát x(k+1)-et egy elemi késleltetés közbeiktatásával vissza kell csatolni a kontroller bemenetére. A teljes elrendezés egy olyan visszacsatolt hálózat, melyben a modell egy már megtanított fix hálózat, a kontroller pedig egy olyan háló, melyet még meg kell tanítani a megfelelő működésre. A tanítás az időbeli kiterítés elvét alkalmazva, tehát BPTT megközelítésben lehetséges.

Ha K időlépésig működtetjük a tanításnál a modell-kontroller együttest, akkor az időbeli kiterítés szerint a fenti elrendezést K-szor meg kell ismételni, ahogy ezt a 8.9 ábra mutatja. Az ábrán a C-vel jelölt blokkok jelentik a kontrollert az M-mel jelöltek pedig a modellt.

ABPTT itteni alkalmazása csak annyiban tér el az általános megoldástól, hogy míg az általános esetben minden lépésben, az autótolatós feladatnál csak az utolsó, K-adik lépésben tudunk hibát meghatározni. Ezt kell visszaterjeszteni a teljes láncon. A súlymódosítás tényleges elvégzése az időbeli kiterítés elvének bemutatásánál mondottak figyelembevételével lehetséges.

A kontroller tanítása úgy történik, hogy egy kezdeti helyzetből indulva megteszünk K tolató lépést, majd meghatározzuk a végpozíció hibáját. Ezt a hibát visszaterjesztve a teljes láncon egy tolatási szekvenciához tartozó súlymódosítás elvégezhető. Kellő számú tolatási szekvenciával történő tanítás után a háló adott tartományon belül bármely kezdeti helyzetből képes a kocsit a végpozícióba vezérelni.

A 8.10 ábra a feladat bonyolultabb változatának egy tipikus eredményét mutatja [Wid90b]. A bonyolultabb változatban a vezetőfülke mögött két pótkocsi van.

Az alábbiakban olyan, visszacsatolt háló-architektúrákra alkalmazható tanulási eljárást mutatunk be, mely a pillanatnyi gradiens alapján valós idejű, lépésenkénti tanítást tesz lehetővé [Wil89].

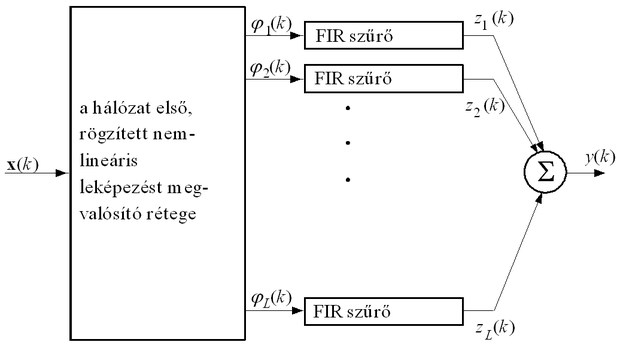
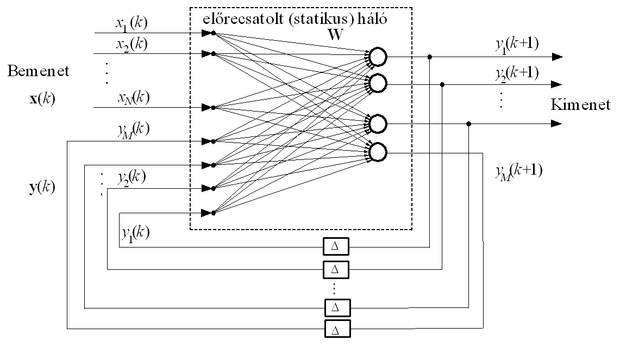
A háló felépítését a 8.11 ábra mutatja. Látható, hogy ez valójában egy globális visszacsatolást tartalmazó háló, hiszen a háló kimenetéről is van visszacsatolás a háló bemenetére, ugyanakkor a háló lokális visszacsatolásokat is tartalmazhat, mivel a statikus háló-kimenetek nem mindegyike képezi a teljes háló kimenetét. Ha az általános modell-struktúrák szerint kategorizáljuk a hálózatot, akkor az alapjában egy NOE struktúrának tekinthető. Ha azonban figyelembe vesszük, hogy van olyan processzáló eleme is, amelyről történik visszacsatolás, de amely közben nem képezi a háló kimenetét, akkor a hálót egy más modell-osztályba tartozónak is tekinthetjük. A visszacsatolt, de a kimenetre ki nem jutó PE-k a háló belső állapotait reprezentálják, így egy nemlineáris állapotteres modellmegadás látszik e struktúra jellemzésére a legalkalmasabbnak.

A rekurzív háló emlékezettel rendelkezik, tehát egy bemeneti szekvenciára egy kimeneti szekvenciával válaszol. A kimenet a $\left(k+1\right)$ -edik időpillanatban a visszacsatolás miatt a következő:

$y_i\left(k+1\right)=f\left[x\left(k\right),y\left(k\right)\right]$ . (8.39)

Az egységes kezelés érdekében vezessük be a következő jelölést. Jelöljük az előrecsatolt háló-rész i-edik bemeneti komponensét $u_i\left(k\right)$ -val:

$u_i\left(k\right)=\{\begin{array}{c}{x}_i\left(k\right)\text{h}\text{a}i\in A\\ y_i\left(k\right)\text{ha}i\in B\end{array}$ (8.40)

ahol A jelöli a bementi indexek halmazát, B a háló azon processzáló elemeinek index-halmazát, mely processzáló elemek kimenetét visszacsatoljuk. Ezzel a háló kimenete

$y_i\left(k+1\right)=f\left[s_i\left(k\right)\right]=f\left[{\displaystyle \sum _{j\in A\cup B}{w}_{ij}{u}_j\left(k\right)}\right]$ , (8.41)

vagy az eredeti jelölésekkel

$y_i\left(k+1\right)=f\left[{\displaystyle \sum _{j\in A}{w}_{ij}{x}_j\left(k\right)+{\displaystyle \sum _{j\in B}{w}_{ij}{y}_j\left(k\right)}}\right]$ (8.42)

A hiba a háló azon kimenetein értelmezhető, amelyeknél kívánt választ specifikálunk. Vagyis a hibakomponensek a k-adik időpillanatban:

${\epsilon }_i^2\left(k\right)=\{\begin{array}{c}{\left(d_i\left(k\right)-y_i\left(k\right)\right)}^2\text{ ha }i\in C\left(k\right)\\ 0\text{ egyébként}\end{array}$ (8.43)

Itt C(k) jelöli azon processzáló elem-indexek halmazát, amelyekre kívánt választ specifikálunk a k-adik lépésben. A halmaz lépésfüggő megadása azt jelenti, hogy időlépésenként eltérő neuronokhoz rendelhetünk kívánt választ.

Az eredő pillanatnyi hiba a hibakomponensek összege:

${\epsilon }^2\left(k\right)={\displaystyle \sum _{i\in C(k)}{\epsilon }_i^2\left(k\right)}$ (8.44)

A megfelelő működés eléréséhez a tanítás során a teljes szekvencia alatti eredő hibát, vagyis a pillanatnyi hibák teljes szekvenciára, mint időablakra vett összegét kell minimalizálnunk.

${\epsilon }^2={\displaystyle \sum _{k=1}^{{\rm K}}{\epsilon }^2\left(k\right)}$ (8.45)

A gradiens módszer alkalmazásakor ennek a teljes hibának a súlymátrix szerinti gradiensét:

$\frac{\partial {\epsilon }^2}{\partial W}={\displaystyle \sum _k\frac{\partial {\epsilon }^2\left(k\right)}{\partial W}}$ (8.46)

kell meghatároznunk és a szokásos módon, a negatív gradiens irányában kell változtatnunk a súlyokat. A gradiens számítás az egyes időpillanatokbeli gradiens számítás felhasználásával elvégezhető. Ennek megfelelően minden egyes időpillanathoz tartozik egy súlymódosítás, és ezen súlymódosítások adott időablakra vett összege adja a tényleges súlymódosítás értékét. Itt súlykorrekció nyilvánvalóan nem történhet minden időpillanatban, hiszen az időablakon belüli hibameghatározás és súlykorrekció-számítás feltételezi, hogy közben a súlyok nem változnak, tehát a háló ezen időlépések alatt rögzített. A tanítást szakaszosan végezzük, egy szakaszban tulajdonképpen az összes tanítópontot, tehát a teljes tanítószekvenciát egyszer felhasználjuk.

Az időablakra számított teljes hiba alapján történő tanítás tehát − hasonlóan az előző pontban bemutatott tanításhoz − nem végezhető el valós időben. A valós idejű hálózat-módosításhoz a pillanatnyi hiba gradiensét minden egyes lépésben kiszámítjuk és minden lépésben el is végezzük a súlyok módosítását. Ez azt jelenti, hogy a háló "emlékezetének" ideje alatt is változik maga a háló, igazában tehát nem a valódi gradiens irányában történik a súlymódosítás. E módszer a legmeredekebb lejtő eljárásnak csupán közelítését adja. Az eltérés a "valódi" és a közelítő gradiens között annál kisebb, minél óvatosabb a lépésenkénti súlymódosítás, tehát minél kisebb a tanulási tényező. Megfelelően kis μ alkalmazása esetén a valós idejű tanítás a valódi gradiens alapú tanítás jó közelítése lesz. Az eljárás előnye, hogy egyszerűbb, minden újabb tanítópont felhasználásánál azonos módon kell eljárnunk, nem kell tárolnunk, illetve akkumulálnunk az egyes lépésekhez tartozó súlymódosító értékeket, nem kell blokkosan végezzük a tanítást. A súlymódosítás alapösszefüggései a kétféle megközelítésben azonosak, különbség tehát csak az elemi súlymódosítások felhasználásában van. A módszer alkalmazhatóságát szimulációs vizsgálatok és gyakorlati alkalmazások igazolják. Az alábbiakban a tanítási összefüggések származtatását mutatjuk be.

A súlykomponensekre vonatkoztatott pillanatnyi gradiens az alábbi formában határozható meg:

$\frac{\partial {\epsilon }^2\left(k\right)}{\partial w_{ij}}={\displaystyle \sum _{l\in C}\frac{\partial {\epsilon }_l^2\left(k\right)}{\partial w_{ij}}}$ (8.47)

A megfelelő súly módosítását meghatározó összefüggés:

$\Delta w_{ij}\left(k\right)=-\mu \frac{\partial {\epsilon }^2\left(k\right)}{\partial w_{ij}}$ , (8.48)

ahol μ most is a tanulási tényező (bátorsági faktor). A gradienst továbbírva kapjuk, hogy:

$\begin{array}{l}\frac{\partial {\epsilon }^2\left(k\right)}{\partial w_{ij}}=2{\displaystyle \sum _{l\in C}{\epsilon }_l\left(k\right)}\frac{\partial {\epsilon }_l\left(k\right)}{\partial w_{ij}}\\ \text{ =-}2{\displaystyle \sum _{l\in C}{\epsilon }_l\left(k\right)}\frac{\partial y_l\left(k\right)}{\partial w_{ij}}\end{array}$ (8.49)

A $\frac{\partial y_l\left(k\right)}{\partial w_{ij}}$ parciális deriváltat a háló dinamikáját leíró (8.41), ill. (8.42) egyenleteket figyelembe véve kapjuk meg:

$\frac{\partial y_l\left(k+1\right)}{\partial w_{ij}}=f^{\prime }\left(s_l\left(k\right)\right)\frac{\partial s_l\left(k\right)}{\partial w_{ij}}$ , (8.50)

ahol

$s_l\left(k\right)={\displaystyle \sum _{r\in A}{w}_{lr}}{x}_r\left(k\right)+{\displaystyle \sum _{r\in B}{w}_{lr}}{y}_r\left(k\right)={\displaystyle \sum _{r\in A\cup B}{w}_{lr}}{u}_r\left(k\right)$ . (8.51)

Tehát

$\begin{array}{l}\frac{\partial y_l\left(k+1\right)}{\partial w_{ij}}=f^{\prime }\left(s_l\left(k\right)\right){\displaystyle \sum _{r\in A\cup B}\frac{\partial \left[w_{lr}{u}_r\left(k\right)\right]}{\partial w_{ij}}}\\ =f^{\prime }\left(s_l\left(k\right)\right){\displaystyle \sum _{r\in A\cup B}\left[\frac{\partial w_{lr}}{\partial w_{ij}}{u}_r\left(k\right)+\frac{\partial u_r\left(k\right)}{\partial w_{ij}}{w}_{lr}\right]}\end{array}$ (8.52)

Felhasználva, hogy $\frac{\partial w_{lr}}{\partial w_{ij}}=1$ , ha l=i és r=j, egyébként a két súly között nincs kapcsolat, tehát a derivált értéke 0:

$\frac{\partial w_{lr}}{\partial w_{ij}}={\delta }_{li}$ , (8.53)

ha r=j, (itt δ_li a Kronecker delta) és hogy

$\frac{\partial u_r\left(k\right)}{\partial w_{ij}}=\{\begin{array}{c}0\text{ha}r\in A\\ \frac{\partial y_r\left(k\right)}{\partial w_{ij}}\text{ha}r\in B,\end{array}$ (8.54)

$\frac{\partial y_l\left(k+1\right)}{\partial w_{ij}}=f^{\prime }\left(s_l\left(k\right)\right)\left[{\displaystyle \sum _{r\in B}{w}_{lr}\frac{\partial y_r\left(k\right)}{\partial w_{ij}}+{\delta }_{li}{u}_j\left(k\right)}\right]$ . (8.55)

Fenti összefüggés a parciális deriváltra egy rekurzív összefüggés, amelynek kiértékeléséhez természetes feltételezés, hogy a kiinduló érték

$\frac{\partial y_l\left(0\right)}{\partial w_{ij}}=0$ . (8.56)

A lépésenkénti súlymódosítás a fentiek felhasználásával tehát:

$w_{ij}\left(k+1\right)=w_{ij}\left(k\right)+2\mu {\displaystyle \sum _{l\in C}\left\{{\epsilon }_l\left(k\right)f^{\prime }\left(s_l\left(k\right)\right)\left[{\displaystyle \sum _{r\in B}{w}_{lr}\frac{\partial y_r\left(k\right)}{\partial w_{ij}}+{\delta }_{li}{u}_j\left(k\right)}\right]\right\}}$ , (8.57)

ahol $i\in B,j\in A\cup B,l\in Césr\in B$ .

A valós idejű eljárás hátránya, mint említettük, hogy nem pontosan a negatív gradiens mentén történnek a korrekciós lépések. Ez nagyon hasonló a standard hibavisszaterjesztéses eljárásnál alkalmazott módszerhez akkor, ha minden egyes tanítópont után végzünk súlymódosítást és nem csak a batch tanításanál szokásos módon, amikor csak a teljes tanító sorozatokat (epochokat) követően történik súlymódosítás.

A Ronald Williams és David Zipser által javasolt eljárásnak több módosított verzióját is kidolgozták. A valódi gradiens és a pillanatnyi gradiens alapján történő számítások közötti átmenet különösen akkor gyorsítja a konvergenciát, ha a hálóval feldolgozandó bemeneti jel-szekvencia nagyon hosszú. Tony Robinson és Frank Fallside [Rob91] olyan hálózat tanítására adott a fentiektől eltérő megoldást, ahol visszacsatolás a valódi kimenetekről − tehát amely neuronokhoz kívánt válaszokat is rendelünk − nincs, csupán a háló többi − valójában rejtett − neuronjának kimeneteit csatoljuk vissza.