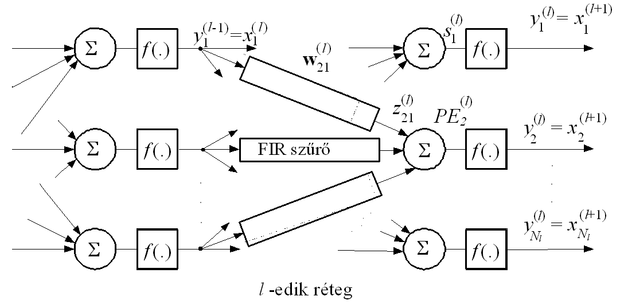
A FIR-MLP hálózat felépítését a 8.4 ábra mutatja. Látható, hogy ez a dinamikus struktúra egy olyan MLP hálózat, ahol minden súly helyett egy lineáris FIR szűrő szerepel. Ez alól csak az egyes neuronok eltolás (bias) bemenetei a kivételek, amelyeknél meghagyjuk a statikus kapcsolatot biztosító súlyértéket. Az ábrán azonban ezek az eltolás bemenetek a jobb áttekinthetőség érdekében nem szerepelnek. A struktúra előnye a bemeneti késleltető lánc alkalmazásával szemben, hogy miközben itt a bemenetek számát nem növeltük meg, és ezáltal várhatóan nincs szükség a rejtett neuronok számának megnövelésére sem, az előrecsatolt dinamikus működést biztosítjuk. A szabad paraméterek száma természetesen egy hasonló méretű (hasonló neuronszámú) statikus MLP-hez képest megsokszorozódik.
A hálózat tanításához először a kimeneti hiba (8.10) szerinti összefüggését kell felírni. Az eredő hiba a háló összes kimenetén értelmezhető, adott időpillanathoz tartozó négyzetes hibakomponensek mind a kimenetek, mind a K időablak szerinti összege (NL a kimeneti réteg neuronjainak száma). Jelöljük ezt a hibát ε2-tel.
, (8.11)
Egy adott súly módosításához ennek az eredő négyzetes hibának az adott súly szerinti deriváltját kell meghatározni. Célszerű azonban, ha közvetlenül egy összeköttetés-ágban szereplő FIR szűrő összes együtthatóját összefogó súlyvektor tanító összefüggését írjuk fel.
Vezessük be ehhez a következő jelölést. Legyen
(8.12)
az l-edik réteg i-edik és az előző réteg j-edik processzáló eleme közötti szűrő együtthatóinak vektora. A vektor felírásából látható, hogy a szűrőágban
egységnyi késleltetés és
szűrőegyüttható van. Bár elvileg nincs akadálya, hogy az egyes szűrők eltérő számú késleltetést tartalmazzanak, ennek gyakorlati haszna nincs, ezért most is feltételezzük, hogy egy adott réteg összes neuronjának minden bemeneti szűrője azonos számú késleltetéssel és ennek megfelelően azonos számú szűrő együtthatóval rendelkezik. Ezért
minden i=1,2,…, N(l-1) és minden j=1,2,…,Nl-re (N(l-1) és Nl az (l−1)-edik, illetve az l-edik réteg neurojainak a száma).
A fentiek figyelembevételével a súlymódosító összefüggéshez a
gradiens meghatározása szükséges. A háló tanítási összefüggéseinek meghatározása többféle megközelítésben lehetséges. Egy lehetőség, ha a
gradienst az egyes időpillanatokhoz tartozó
gradiensek segítségével írjuk fel:
. (8.13)
Itt tehát
, vagyis az eredő négyzetes hiba az egyes időpillanatokbeli négyzetes hibaértékek megfelelő időablakra vett összegét jelenti. E megközelítés szerint végezve a vizsgálatot valójában időben kiterítjük a hálózatot és így egy nagyobb, de statikus hálót kapunk, ami már a hagyományos hibavisszaterjesztéses algoritmussal tanítható. A kiterítés következtében kapott virtuális háló azonban igen nagyméretű is lehet a FIR szűrőkben található késleltető láncok méretétől függően, továbbá a virtuális háló struktúrája el fog térni a szokásos többrétegű perceptron felépítésétől: az egyes rétegek processzáló elemei nincsenek a következő réteg összes processzáló elemével összekötve. További eltérés, hogy a virtuális háló az időbeli kiterítés következtében jóval több súlyt tartalmaz, mint a fizikailag létező valóságos; egy valóságos súlynak a virtuális hálóban több megfelelője van, melyek a háló működésének különböző időpillanataihoz tartoznak és a kiterített hálóban más-más rétegben szerepelnek. A hagyományos hibavisszaterjesztéses algoritmus alkalmazásánál az azonos fizikai súly különböző virtuális megfelelőihöz eltérő súlymódosító összefüggéseket kapunk, mivel a hibavisszaterjesztés útja a különböző virtuális megfelelőkig eltérő. Ennek ellenére csak egy fizikai súly létezik, tehát ezt különbözőképpen nem módosíthatjuk. A megoldás csak az lehet, hogy a különböző módon visszaterjesztett "hiba" figyelembevételével nyert súlymódosítások eredőjével kell módosítanunk a fizikai súly értékét, ami azt jelenti, hogy a megfelelő virtuális súlyok azonos mértékben és egyszerre módosulnak.
E nehézségek miatt, különösen nagyobb rendszereknél az időbeli kiterítés alapján történő FIR-MLP tanítás − bár elvileg lehetséges − nem célszerű. A következőkben egy más megközelítést mutatunk be.
Temporális hibavisszaterjesztéses eljárás
A temporális hibavisszaterjesztéses(temporal back-propagation) eljárás a FIR-MLP háló tanítására egy hatékonyabb lehetőség [Wan90]. A kimeneti eredő hiba gradiense ugyanis a (8.13)-tól eltérően másféle felbontásban is felírható (a temporális back-propagation eljárás származtatásánál a 8.4 ábra jelöléseit illetve az MLP tanításánál, a standard hibavisszaterjesztéses eljárásnál alkalmazott jelöléseket használjuk):
. (8.14)
Itt tehát nem a pillanatnyi négyzetes hiba adott súlyvektor szerinti gradiensét határozzuk meg először, amiből a megfelelő időablakra vonatkozó összegzéssel határozható meg az eredő gradiens, hanem az eredő hibának a megfelelő kimenet adott időpillanatbeli értéke szerinti parciális deriváltján keresztül kapjuk meg az eredő gradienst. Vegyük észre, hogy
, (8.15)
vagyis bár (8.13) és (8.14) egyenlők, adott k időindexhez tartozó komponenseikre az egyenlőség már nem áll fenn. Megmutatható, hogy ez utóbbi megközelítést választva a FIR-többrétegű perceptron tanítása a standard BP eljáráshoz hasonlóan történhet, vagyis a hibavisszaterjesztés itt is a jel előreterjesztését végző hálózathoz hasonló hálózaton, most tehát FIR szűrőkön keresztül történik.
A (8.14) szerinti felbontás alapján a következő súlymódosító összefüggést nyerjük:
. (8.16)
A (8.16)-nak megfelelő súlymódosítás természetesen nem pontosan az igazi gradiens szerint halad a megoldás térben, hiszen egy módosító lépésben az eredő teljes hiba gradiense helyett egy gradiens-komponenssel dolgozunk. Nem túl nagyra választva azonban μ értékét, a súlymódosítás közel a valódi gradiensnek megfelelően történik. Megjegyezzük azonban, hogy a gradiens-komponens nem csak egy időpillanatbeli hiba alapján számítódik, hiszen a súlymódosításhoz
megfelelő deriváltját használjuk fel.
Mivel a standard hibavisszaterjesztéses algoritmushoz hasonlóan
, továbbá, ha most is használjuk a
jelölést, akkor egy adott súly helyén található szűrőegyütthatókból álló vektor módosítására az alábbi, a statikus MLP tanításávalformailag azonos összefüggést kapjuk:
. (8.17)
A visszaterjesztett, általánosított hiba (valójában a kimeneti négyzetes hibának egy adott neuron lineáris kimenete szerinti érzékenysége) meghatározása attól függ, hogy az adott neuron melyik rétegben található.
A kimeneti réteg esetén
egyszerűen meghatározható, hiszen:
(8.18)
Így a kimeneti réteg neuronjainál a súlyok módosítására formálisan a standard back-propagation eljárás kimeneti rétegre vonatkozó összefüggését kapjuk:
. (8.19)
Az egyetlen különbség, hogy itt
nem a kimeneti réteg összes súlyából álló súlyvektor, hanem a megfelelő szűrőág együtthatóiból álló, (8.12) által definiált vektor. Ugyancsak
nem az L-edik réteg teljes bemeneti vektora, hanem minden kimeneti neuron j-edik szűrőágában a késleltetett bemenetekből képezett vektor:
(8.20)
Ez a vektor természetesen megegyezik az előző réteg j-edik neuronjának késleltetett kimeneteiből képezett vektorral.
Az adott szűrő tehát
késleltető tagot tartalmaz, és a szűrő kimenetét a
, (8.21)
kapcsolat adja meg. A rejtett rétegeknél
meghatározásában a statikus hálónál származtatott hibavisszaterjesztéses algoritmushoz hasonlóan szerepet játszik az összes olyan neuron, mely összeköttetésben van az l-edik réteg i-edik neuronjának kimenetével, vagyis az (l+1)-edik réteg összes neuronja. A FIR szűrőben lévő késleltető lánc miatt azonban itt az időt is figyelembe kell venni. Ugyanis
a következő rétegbeli neuronok kimeneteinek nemcsak a k-adik időpillanatbeli értékét, hanem több, a k-adikat követő időpillanatbeli értékét is befolyásolja.
Mivel
a teljes négyzetes hiba
szerinti deriváltja, ezt az időfüggést nem hagyhatjuk figyelmen kívül.
meghatározása most is a láncszabály alkalmazásával lehetséges:
(8.22)
Itt t szintén diszkrét időindex, és azokat az időpillanatokat jelöli, amelyekben az (l+1)-edik réteg kimenetei függnek az l-edik réteg i-edik neuronjának lineáris kimenetétől,
-tól. Mivel teljesen összekötött hálót tételezünk föl, egy adott réteg minden kimenete kapcsolódik a következő réteg összes neuronjához. Ebből adódóan m végigfut az 1, …, N(l+1) értékeken.
A (8.22) kifejezés első tényezőjét nézve azonnal látható, hogy
. A második tényezőt tovább írva:
. (8.23)
Az egyenlet tovább alakításához figyelembe kell vennünk
keletkezését. Ez az (l+1)-edik réteg m-edik neuronjának lineáris kimenete, amit nyilvánvalóan a neuron bemenetére csatlakozó szűrők kimeneteinek összegeként kapunk:
(8.24)
ahol
az (l+1)-edik réteg m-edik neuronja j-edik bemeneti szűrőágának kimenete:
. (8.25)
Itt
a j-edik szürőág bemenetére kerülő késleltetett értékekből álló vektor:
. (8.26)
Egy neuron bemenetén annyi szűrőág van, ahány neuron van az előző rétegben. A (8.23) összefüggésben az i-edik szűrőág szerepel, ugyanis
a
neuron (az (l+1)-edik réteg m-edik neuronja) bemeneti szűrői közül csak az i-edikre jut. Ennek kimenete:
, (8.27)
melynek felhasználásával:
, (8.28)
ha k=t-p. Figyelembe véve, hogy az (l+1)-edik réteg minden neuronjának szűrőiben
egységnyi késleltetés van, vagyis a szűrőegyütthatók száma
, (8.28)-ra a következőt kapjuk:
. (8.29)
Ennek figyelembevételével a rejtett rétegre vonatkozó
-ra
(8.30)
adódik. Alkalmazva a p=t−k jelölést
(8.31)
ahol
. (8.32)
Összefoglalva:
(8.33)
A (8.31) és a (8.32) összefüggésekből viszont látható, hogy
meghatározásához a rejtett rétegnél olyan szűrő szükséges, amelynek együtthatói a megfelelő előrevezető ág szűrőegyütthatói, a szűrt értékek pedig jövőbeli
értékek (
). A súlymódosítást meghatározó összefüggés tehát nem kauzális.
A számítás kauzálissá tehető, ha a hálózat megfelelő pontjain alkalmas késleltető fokozatokat iktatunk be. A késleltetések közbeiktatása azt eredményezi, hogy a súlyvektorok módosításához csak az aktuális és a korábbi hibák ismerete szükséges.
A kimeneti réteg súlyvektorainak módosítása a fenti összefüggések szerint történhet, hiszen ott eddig sem merült föl nem kauzális számítási igény. A rejtett rétegek számítása pedig az alábbiak szerint lehetséges:
(k) helyett a
(k−M(l+1)) visszaterjesztett "hibát" határozzuk meg, tehát a k indexet (k−M(l+1))-re cseréljük és ezzel a visszaterjesztett hibával határozzuk meg a rejtett réteg súlyvektorainak módosítását. Azonban a (8.17) összefüggés szerinti súlymódosításhoz
(k) helyett is
(k−M(l+1)) szükséges, vagyis a megfelelő bemeneti vektorokat tárolni kell.
Összefoglalva: a kauzális számítás a következő összefüggések alapján végezhető:
– a kimeneti réteg i-edik neuronjához vezető súlyvektoroknál:
, (8.34)
ahol
, (8.35)
– az l-edik (rejtett) réteg i-edik neuronjánál:
, (8.36)
ahol
, (8.37)
és
, (8.38)
Ha a hálóban több rejtett réteg található, akkor a fenti összefüggések a kimenethez legközelebbi rejtett rétegre vonatkoznak, a kimenettől egyre távolabbi rejtett rétegeknél az indexeltolás egyre nagyobb mértékű, a FIR szűrő késleltető-láncok hosszának összege kell legyen.
A fenti összefüggések azt mutatják, hogy a FIR-MLP hálózat temporális hibavisszaterjesztő tanításánál a hibavisszaterjesztő hálózat felépítése az előreterjesztő hálózatstruktúrához hasonló: a visszaterjesztett általánosított hiba a megfelelő előreterjesztő ágakban lévő szűrőkön keresztül jut az egyre előbbi rétegekhez. A visszaterjesztő hálózatnál tehát itt is megtaláljuk a klasszikus statikus MLP hálózatnál származtatott BP eljárás reciprok voltát, a hálózat eredeti struktúrája is megmaradt szemben az időbeli kiterítés módszerének alkalmazásával.
A FIR-MLP háló képességei igen kedvezőnek bizonyultak idősor modellezési feladatoknál, továbbá nemlineáris dinamikus rendszerek modellezésénél, identifikációjánál [Wan94].
Megjegyezzük, hogy a FIR-MLP struktúrához némileg hasonló az ún. késleltetéses neuronháló (Time Delay Neural Network, TDNN), melyet elsődlegesen beszédjelek osztályozására dolgoztak ki [Lan88], [Wai89]. A TDNN nem szűrőket alkalmaz az MLP súlyai helyén, hanem az egyes neuronokat többszörözi meg úgy, hogy az egyes ismétlések eltérő időpillanatbeli értékekkel dolgoznak. A rétegek között nem teljes az összeköttetési rendszer. Egy későbbi (pl. rejtett) réteg adott időpillanathoz tartozó minden neuronja az előbbi (pl. bemeneti) réteg neuronjainak (a bemeneteknek) egy keskeny idősávhoz tartozó neuron-másolataival (értékeivel) van összeköttetésben mégpedig úgy, hogy az eltérő időpillanatokhoz eltérő idősávok tartoznak, miközben az eltérő időpillanatokhoz tartozó neuron-másolatok azonos súlyokkal rendelkeznek.