A neurális dinamikus modellekkialakításának több útja lehet. A legkézenfekvőbb megoldás, ha egy eredetileg statikus neuronhálót dinamikus elemekkel egészítünk ki. A dinamikus elemek megjelenhetnek a statikus háló bemeneteinél, de a háló "belsejében" is [Ner93], [Dre05]. A nemlineáris statikus és a lineáris dinamikus hálók ötvözeteként létrehozott nemlineáris dinamikus rendszerekre további példát jelentenek azok a kaszkád hálózatok, ahol lineáris dinamikus és nemlineáris statikus rendszerek szerepelnek valamilyen sorrendben a jelútban. Ilyen rendszerek pl. a Wiener, a Hammerstein, illetve a Wiener-Hammerstein modellek [Bal00]. E speciális felépítésű "hálók" ugyan korlátozott modellező képességgel rendelkeznek, de tárgyalásuk az általános esetnél egyszerűbb lehet, és számos gyakorlati feladatnál a "valóság" megfelelő pontosságú modelljének bizonyulhatnak [Nar90], [Bou95], [Pin01].

8.1. ábra - Általános időfüggő neurális hálózat többdimenziós bemenet és egydimenziós kimenet mellett

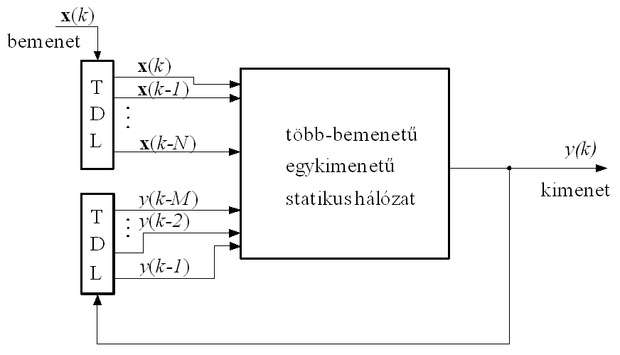
Az időfüggés beépítésének triviális módja, ha a hálózat bemeneteinek számát megnöveljük és az egyes bemenetekre a tényleges be- és/vagy kimenőjelek késleltetett értékeit adjuk megfelelő késleltető láncokon (tapped delay line: TDL) keresztül (8.1 ábra). Az ábra valójában egy NOE modellstruktúrát mutat, de ebből a felépítésből egyszerűsítéssel vagy kis módosítással a többi bemenet-kimenet reprezentáción alapuló modellosztálynak megfelelő neurális architektúra is származtatható. Amennyiben csak az x bemenőjelnél alkalmazzuk a késleltető láncot és a háló nem tartalmaz visszacsatolást, a dinamikussá tett háló NFIRstruktúrát valósít meg. Ha az ábra szerinti visszacsatolás is jelen van NOE, vagy párhuzamos modellt kapunk. A kimenetről történő visszacsatolás helyett a kívánt választ "csatolva vissza" NARXvagy soros-párhuzamos modellt nyerünk.

8.2. ábra - Állapotváltozós modell neurális implementációja

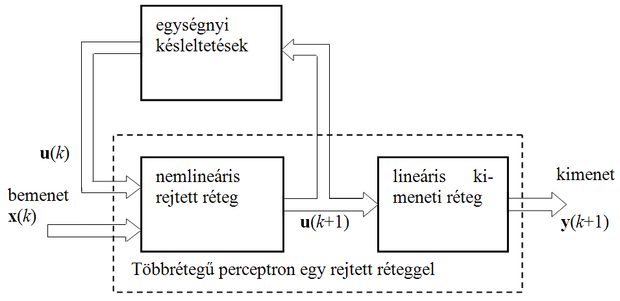
Látható, hogy minden esetben valójában továbbra is statikus hálózattal van dolgunk, az időfüggő viselkedést a hálózat megfelelően képzett bemenetei biztosítják. Az 8.1 ábrán bemutatott általános háló-felépítés az input-output reprezentációnak felel meg. Hasonló általános neurális struktúrát adhatunk meg az állapotváltozósleíráshoz. Ezt mutatja a 8.2 ábra.

Az előbbi ábrákon bemutatott megoldások gyakorlati alkalmazása a bemenetek számának esetleges nagymértékű növelése miatt nem mindig célszerű, bár az így kapott hálók általános időfüggő hálózatok kialakítására alkalmasak. Más megoldásokkal nem a bemeneteken keresztül vezetünk be időfüggést, hanem a hálózat belső felépítését módosítjuk olyan módon, hogy az időfüggő viselkedést mutasson.

8.3. ábra - Példa lokális visszacsatolásokra

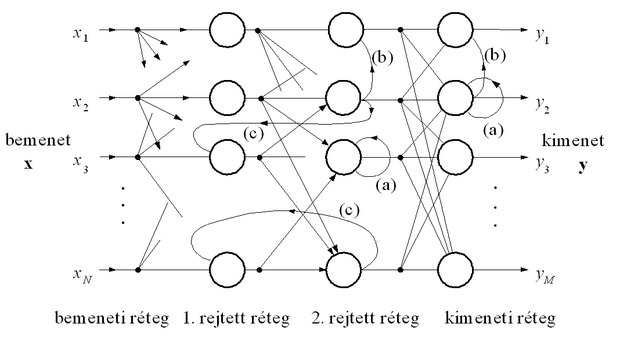
A belső felépítés módosítása jelentheti dinamikus, memóriával rendelkező neuronokalkalmazását (ld. 1.1. ábra), lineáris dinamikus rendszerek, lineáris szűrők beépítését a hálóba, illetve lokális visszacsatolásokalkalmazását. A lokális visszacsatolás(oka)t tartalmazó hálók számos változatát dolgozták ki. A 8.3 ábrán néhány visszacsatolási lehetőségre mutatunk példát.

A többrétegű perceptronnál a szokásos előrecsatoló összeköttetéseket csak vázlatosan jelöltük. Egy processzáló elem lehet önmagában visszacsatolt (a), de lehet az egy rétegen belüli processzáló elemek között oldalirányú kapcsolat (b), ill. kialakíthatunk visszacsatolást egy későbbi rétegről egy valamelyik előbbire is (c).

A visszacsatolt hálózatok modellező képessége a csak előrecsatolást tartalmazó dinamikus hálózatokénál nagyobb, de használatuknál számos nehézség merül fel. Egyrészt a visszacsatolás miatt stabilitási problémák léphetnek fel, másrészt a hálózatok tanítása lényegesen bonyolultabb lehet.

Az időfüggő hálózatokat, ha jel-szekvencia felismerésre, szekvencia reprodukálására és folytatására (jóslás, előrejelzés) vagy egy bemeneti szekvenciára kimeneti válasz-szekvencia generálására alkalmazzuk, szokás szekvenciális hálózatoknak is nevezni. (A visszacsatolt hálózatok egy másik csoportjánál a bemenetre kerülő minta hatására egy tranziens indul el, miközben a hálózat bemenete nem változik, és a tranziens lezajlása utáni állandósult állapothoz (egyensúlyi állapot) tartozó kimenetet tekintjük a hálózat válaszának. Ilyen pl. a Hopfield hálózat, mellyel nem itt, hanem a 11. fejezetben foglalkozunk.)

Az időfüggő hálózatok és a statikus hálózatok közötti legjelentősebb különbség a hálózat válaszának minősítése és a hálózat tanítása szempontjából, hogy míg a statikus hálóknál egy bemeneti mintára adott kimeneti válasz önmagában értékelhető, addig az időfüggő hálózatok értékelése bemeneti szekvenciákra adott kimeneti szekvenciák alapján történhet csak. A hálózat viselkedése ezért általában egy adott időpillanathoz tartozó kimeneti hiba alapján nem minősíthető, hanem a kimeneti hiba valamely időintervallumra vett átlagának vagy összegének meghatározására van szükség, és azt kell vizsgálnunk, hogy ezen eredő hiba hogyan csökkenthető a hálózat paramétereinek megválasztásával.

Ha az eddigiekhez hasonlóan a kimeneti pillanatnyi hibát $\epsilon \left(k\right)$ -val jelöljük, akkor az eredő négyzetes hiba:

${\epsilon }^2={\displaystyle \sum _{k=1}^{{\rm K}}{\epsilon }^2\left(k\right)={\displaystyle \sum _{k=1}^K{\left|d\left(k\right)-y\left(k\right)\right|}^2}}$ , (8.10)

ahol k most is a diszkrét időindexet, K pedig a háló működésének szempontjából fontos időablak méretét jelöli. A hálózat gradiens alapú eljárással történő tanításához tehát az eredő hibának a megfelelő súly vagy súlyvektor szerinti deriváltját $\left(\frac{\partial {\epsilon }^2}{\partial w_{ij}}\right)$ -t kell meghatározni. Az egyes hálózatoknál alkalmazott tanítóeljárások, a hálózat struktúrájából adódó eltéréseken kívül, abban is különböznek, hogy e deriváltak meghatározása hogyan történik, illetve, hogy a tanító eljárások a derivált pontos vagy közelítő meghatározásán alapulnak-e.

Az eddigiekből látható, hogy dinamikus feladatra igen sokféle neuronháló architektúra alkalmazható. Bár e hálók többé-kevésbé besorolhatók valamely általános modellosztályba, a különböző hálók analízise, tanítási összefüggéseinek meghatározása mind-mind egyedi problémákat is felvet. A sokféle dinamikus neurális architektúra áttekintésére nincs módunk, a részletes bemutatástól pedig mindenképpen el kell tekintenünk. A továbbiakban ezért néhány, a gyakorlati alkalmazás szempontjából fontos háló-architektúrát választunk ki és csak ezek felépítését, tanítási összefüggéseit tárgyaljuk. Az érdeklődők a témakört részletesebben az igen bő irodalomból ismerhetik meg (ld. pl. [Gup03], [Dre05]).