Az osztályozásifeladat a már megszokott: adott egy ${\left\{x_i,d_i\right\}}_{i=1}^P$ tanítópont-halmaz, ahol $x_i\in R^N$ egy N-dimenziós bemeneti vektor, illetve $d_i\in \left\{\mathrm{0,1}\right\}$ az ehhez tartozó kívánt kimenet. A cél egy olyan modell létrehozása, ami jól reprezentálja a tanítópontok által leírt kapcsolatot.

Az osztályozó esetében az optimalizálási feladat az alábbi:

$\underset{w,b,e}{\text{min}}J\text{(}w,b,e\text{)}=\frac{1}{2}{w}^{T}w+C\frac{1}{2}{\displaystyle \sum _{i=1}^P{e}_i^2}$ (6.79)

a

$d_i\left[w^T\phi \left(x_i\right)+b\right]=1-e_i$ , $i=\mathrm{1,...,}P$ (6.80)

mellékfeltételekkel. A fenti képletben a négyzetes hibát megadó e_i értékek a négyzetes költségfüggvényből adódó hibaértékek. Szerepük az SVM-ben bevezetett ${\xi }_i$ gyengítő változóknak felel meg. Látható, hogy a feltételekben az SVM osztályozóhoz képest (lásd (6.24) összefüggés) az egyenlőtlenség helyett egyenlőség szerepel, valamint hogy a célfüggvényben a hiba négyzete ( $e_i^2$ ) jelenik meg.

Az osztályozó most is a szokásos bázisfüggvényes alakban írható fel:

$y\text{(}x\text{)}=\text{sign}\left[w^T\phi \left(x\right)+b\right]$ (6.81)

ahol a $\phi \text{(}\text{.)}:R^N\to R^M$ leképezés az SVM-ben is használt nemlineáris leképezés egy magasabb, M-dimenziós jellemzőtérbe.

A fenti egyenletekből az alábbi Lagrange kritérium írható fel:

$L\text{(}w,b,e;\alpha \text{)}=J\text{(}w,b,e\text{)}-{\displaystyle \sum _{i=1}^P{\alpha }_i\left\{d_i\left[w^T\phi \left(x_i\right)+b\right]-1+e_i\right\}}$ , (6.82)

ahol az ${\alpha }_i$ értékek a Lagrange multiplikátorok, amelyek az egyenlőségi feltételek miatt itt pozitív és negatív értékeket is felvehetnek.

Az optimumra vonatkozó feltételek az alábbiak.

$\begin{array}{llll}\frac{\partial L}{\partial w}=0\hfill & \to \hfill & w={\displaystyle \sum _{i=1}^P{\alpha }_i{d}_i\phi (x_i)}\hfill & \hfill \\ \frac{\partial L}{\partial b}=0\hfill & \to \hfill & {\displaystyle \sum _{i=1}^P{\alpha }_i{d}_i=0}\hfill & \hfill \\ \frac{\partial L}{\partial e_i}=0\hfill & \to \hfill & {\alpha }_i=C{e}_i\hfill & i=\mathrm{1,...,}P\hfill \\ \frac{\partial L}{\partial {\alpha }_i}=0\hfill & \to \hfill & d_i\left[w^T\phi \left(x_i\right)+b\right]-1+e_i=0\hfill & i=\mathrm{1,...,}P\hfill \end{array}$ (6.83)

A fenti egyenletekből egy lineáris egyenletrendszer írható fel, mely az alábbi kompakt formában is megadható:

$\left[\begin{array}{cc}0& d^T\\ d& \Omega +C^{-1}I\end{array}\right]\left[\begin{array}{c}b\\ \alpha \end{array}\right]=\left[\begin{array}{c}0\\ 1\end{array}\right]$ , (6.84)

ahol:

$\begin{array}{l}{d}^T=\left[d_1,d_2,\mathrm{...},d_P\right]\\ 1^T=\left[\mathrm{1,...,1}\right]\\ {\alpha }^T=\left[{\alpha }_1,{\alpha }_2,\mathrm{...},{\alpha }_P\right]\\ {\text{Ω}}_{i,j}=d_i{d}_j\phi {\left(x_i\right)}^T\phi \text{(}{x}_j\text{)}=d_i{d}_{j}K\text{(}{x}_i\text{,}{x}_j\text{)}i,j=\mathrm{1,...,}P\end{array}$ (6.85)

és I egy megfelelő méretű egységmátrix. Látható, hogy az egyenletrendszer első sora a ${\displaystyle \sum _{i=1}^P{\alpha }_i{d}_i=0}$ feltételt írja le, míg a további sorok a $\frac{\partial L}{\partial {\alpha }_i}=0$ feltételből adódó egyenleteket írják le, behelyettesítve a (6.83)-ban megadott derivált számításokból $w$ -re és $e_i$ -re származtatott összefüggéseket.

Az osztályozó válasza – hasonlóan a hagyományos SVM-hez – a következő alakban írható fel:

$y\text{(}x\text{)}={\displaystyle \sum _{i=1}^P{\alpha }_i{d}_i}K\text{(}x,x_i\text{)}+b$ . (6.86)

Az ${\alpha }_i$ súlyok és a b eltolásérték (bias) a fenti egyenletrendszerből számíthatók. Az eredmény jellemzője, hogy a megoldásban az összes tanítópont szerepel, tehát mind szupport vektor, azaz az egyenlőség használata miatt nincsenek nulla súlytényezők. Ezzel elveszítjük az SVM ritkasági tulajdonságát, nevezetesen, hogy a bemeneti vektoroknak csak egy kis része lesz szupport vektor. Az ${\alpha }_i$ súlyok nagyság szerinti sorba rendezéséből látszik, hogy melyek a fontosabb, illetve melyek a kevésbé fontos bemeneti vektorok. Ezen alapul a később bemutatásra kerülő komplexitás redukciós metszési (pruning) eljárás, ami az SVM ritkasági tulajdonságát adja vissza.

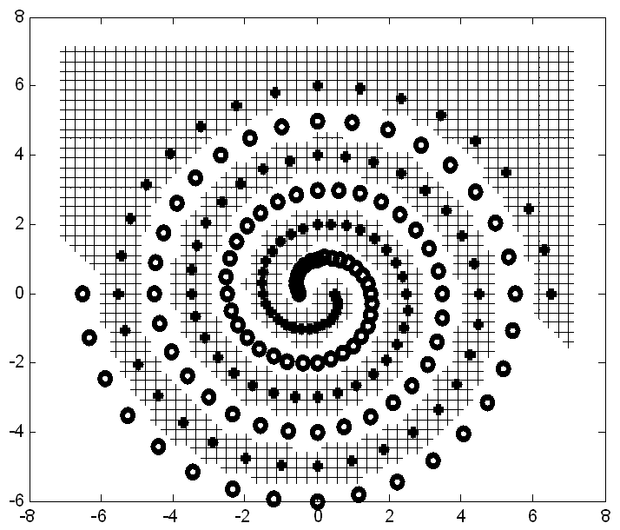
A 6.13 ábrán a szupport vektor gépek összehasonlításánál gyakran alkalmazott kettős spirál probléma LS-SVM-mel történő megoldását mutatjuk. Jól látható, hogy ennél az erősen nemlineáris feladatnál az LS-SVM – hasonlóan az SVM-hez – nagyon jól teljesít.

Az LS-SVM – hasonlóan az eddig látott hálózatokhoz – az osztályozós feladaton túl regressziós esetre is alkalmazható. Ekkor az eddigieknek megfelelően egy $f\left(x\right)$ függvény közelítése a cél adott ${\left\{x_i,d_i\right\}}_{i=1}^P$ tanítópont-halmaz alapján, ahol $x_i\in R^N$ egy N-dimenziós bemeneti vektor és $d_i\in R$ a kívánt kimenet.

A regresszió esetén az optimálási feladat az alábbi:

$\underset{w,b,e}{\text{min}}J\text{(}w,b,e\text{)}=\frac{1}{2}{w}^{T}w+C\frac{1}{2}{\displaystyle \sum _{i=1}^P{e}_i^2}$ (6.87)

a

$d_i=w^T\phi (x_i)+b+e_i$ , ahol $i=\mathrm{1,...,}P$ (6.88)

feltételekkel.

A regresszió válasza a következő alakban írható fel:

$y\text{(}x\text{)}=w^T\phi \left(x\right)+b$ , (6.89)

ahol a $\phi \text{(}\text{.)}:R^N\to R^M$ nemlineáris transzformáció most is a jellemzőtérbe való leképezést biztosítja. Az osztályozós esthez hasonlóan itt is felírhatunk egy Lagrange függvényt:

$L\text{(}w,b,e;\alpha \text{)}=J\text{(}w,b,e\text{)}-{\displaystyle \sum _{i=1}^P{\alpha }_i\left\{w^T\phi (x_i)+b+e_i-d_i\right\}}$ , (6.90)

ahol az ${\alpha }_i$ értékek a Lagrange multiplikátorok. Az optimumra vonatkozó feltételek az alábbiak.

$\begin{array}{llll}\frac{\partial L}{\partial w}=0\hfill & \to \hfill & w={\displaystyle \sum _{i=1}^P{\alpha }_i\phi \text{(}{x}_i\text{)}}\hfill & \hfill \\ \frac{\partial L}{\partial b}=0\hfill & \to \hfill & {\displaystyle \sum _{i=1}^P{\alpha }_i=0}\hfill & \hfill \\ \frac{\partial L}{\partial e_i}=0\hfill & \to \hfill & {\alpha }_i=C{e}_i\hfill & i=\mathrm{1,...,}P\hfill \\ \frac{\partial L}{\partial {\alpha }_i}=0\hfill & \to \hfill & w^T\phi (x_i)+b+e_i-d_i=0\hfill & i=\mathrm{1,...,}P\hfill \end{array}$ (6.91)

A $w$ és az $e$ kifejezése után a következő lineáris egyenletrendszer írható fel:

$\left[\begin{array}{cc}0& 1^T\\ 1& \Omega +C^{-1}I\end{array}\right]\left[\begin{array}{c}b\\ \alpha \end{array}\right]=\left[\begin{array}{c}0\\ d\end{array}\right]$ (6.92)

ahol az $\Omega$ kivételével az egyenletrendszerben szereplő többi jelölés megegyezik a (6.85)-ben megadottakkal. Az $\Omega$ mátrix (i,j)-edik eleme :

${\Omega }_{i,j}=\phi {\text{(}{x}_i\text{)}}^T\phi \text{(}{x}_j\text{)}=K\text{(}{x}_i,x_j\text{)}$ , $i,j=\mathrm{1,...,}P$ . (6.93)

Az eredmény – hasonlóan a hagyományos SVM-hez – a következő alakban írható fel:

$y\text{(}x\text{)}={\displaystyle \sum _{i=1}^P{\alpha }_i}K\text{(}x,x_i\text{)}+b$ , (6.94)

ahol az ${\alpha }_i$ -k és $b$ a fenti lineáris egyenletrendszer megoldásai.

Az egyenletrendszer felírása a parciális deriváltakból az osztályozós esetnél bemutatottak szerint történik. A regressziós esetben azonban az eredmény kiszámítása ((6.94) összefüggés) és az egyenletrendszer sorai között egyértelműen látszik a kapcsolat, nevezetesen, hogy az egyenletrendszer sorai a regularizációt ( $C^{-1}I$ ) leszámítva pontosan megfelelnek az eredmény kiszámítására szolgáló összefüggésnek. Ez nem meglepő, hiszen a tanítópontok által reprezentált feltételek gyakorlatilag azt fogalmazzák meg, hogy az adott bemenetre milyen kimenetet várunk a modelltől. Ez a működés jól követhető a 6.10 ábrán. A tanítás során bevezetett regularizáció pedig megadja, hogy mennyire (mekkora hibával) kell illeszkedni a tanítópontokban. Az erősebb regularizáló hatás pontatlanabb illeszkedést követel és simább (egyszerűbb) megoldást, simább válaszfüggvényt eredményez.

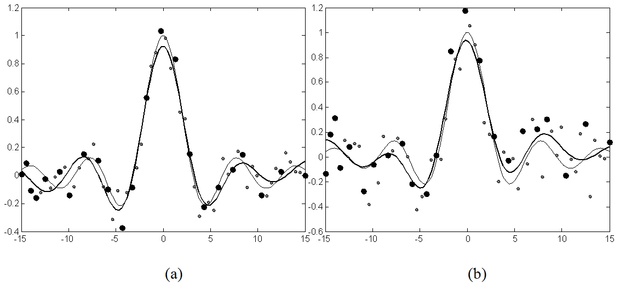
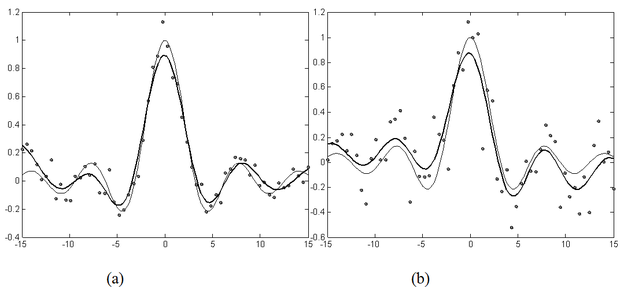
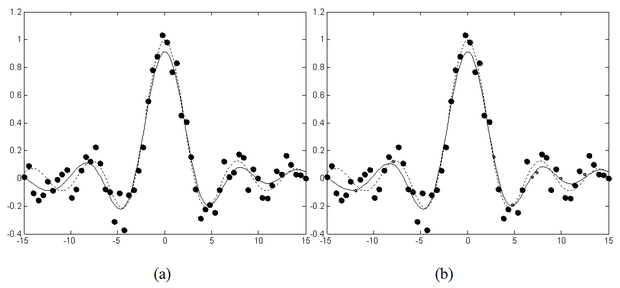
A 6.14 ábrán egy egyszerű példát mutatunk be LS-SVM használatával megoldott regressziós feladatra. Látható, hogy még jelentősebb mértékben zajos tanítópontok mellett is jó megoldást kapunk.

A Least-Squares megoldás egyik hátránya, hogy a megoldás nem ritka (sparse), hiszen mint láttuk, minden tanító vektor szupport vektor is egyben. Ha a végeredményt neurális hálózatként értelmezzük, akkor ebben P (azaz a felhasznált tanítópontok számával megegyező számú) nemlineáris neuron található, így az eredmény komplexitása (a háló mérete) nagyobb, mint a hagyományos SVM-mel nyert hálózatoké, melyek valóban szelektálnak a bementek közül. Ez abból is látszik, hogy a megoldásban felhasználjuk az ${\alpha }_i=C{e}_i$ egyenletet, ami mutatja, hogy a i-edik tanítópontban kapott hiba arányos a tanítóponthoz, mint szupport vektorhoz tartozó ${\alpha }_i$ súllyal. Figyeljük meg, hogy a négyzetes hibafüggvényalkalmazása miatt az $\epsilon$ sáv hiányában gyakorlatilag nincs 0 hibaérték, így nincs ${\alpha }_i=0$ érték sem. Ahhoz, hogy a hagyományos SVM ritkasági tulajdonságát visszanyerjük további lépésekre van szükség.

Intuitíven állíthatjuk, hogy a kisebb ${\alpha }_i$ -k kevésbé járulnak hozzá a megoldáshoz, azaz a kialakított modellhez. A következő „pruning” (metszési) eljárás egy ezen alapuló iteratív módszer, mellyel az LS-SVM alkalmazásánál is elérhető egy egyszerűbb eredmény, azaz kisebb hálózat. A megoldás menete az alábbi:

Tanítsuk a hálózatot az összes rendelkezésre álló (P) tanítóponttal.

Távolítsuk el egy kisebb részét (pl. 5%–át) a pontoknak úgy, hogy azokat hagyjuk el, melyekhez a legkisebb $\left|{\alpha }_i\right|$ -k tartoznak.

Tanítsuk újra az LS-SVM-et a kisebb tanítókészlettel.

Folytassuk a 2. lépéstől, amíg a válasz minősége nem romlik. Ha a teljesítmény romlik, akkor a hiperparaméterek ( $C$ és Gauss kernel esetén a $\sigma$ ) hangolásával esetleg korrigálhatjuk, illetve még tovább csökkenthetjük a megoldás méretét.

A negyedik pontban említett hiperparaméter hangolásának oka jól látható például egy Gauss kerneles hálózat esetén. Ha a metszési (pruning) eljárás eredményeképpen csökken a kernelek száma, akkor az egymástól távolabb eső középpontok miatt gyakran növelni kell a Gauss függvények szélességét ( $\sigma$ ).

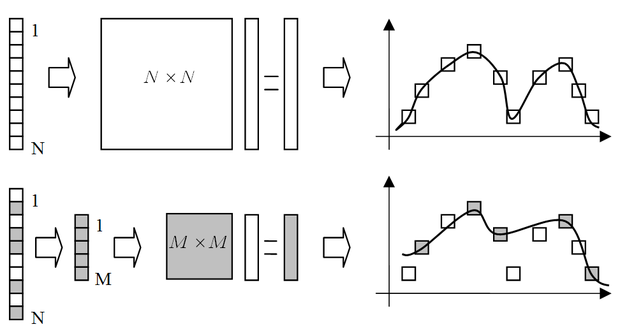
Fontos megjegyezni, hogy a metszési eljárás során, a minták elhagyásával gyakorlatilag a tanítókészlet méretét redukáljuk, ami – főként jelentősebb redukció esetén – információvesztéssel és így a háló minőségének romlásával jár(hat). Ez egyértelmű különbség a Vapnik-féle SVM-hez képest, hiszen ott a ritka megoldást úgy nyertük, hogy közben a Lagrange multiplikátorok meghatározásában az összes tanítópont részt vett. Ennek a kedvezőtlen hatásnak egyfajta mérséklését, vagy kiküszöbölését oldja meg a későbbiekben bemutatásra kerülő LS²-SVM. A mintapontok redukciójának hatását illusztrálja a 1.15 ábra. Az ábrán az üres négyzetek képviselik az összes tanítópontot, az árnyékolt négyzetek pedig a redukált mintakészlet pontjait.

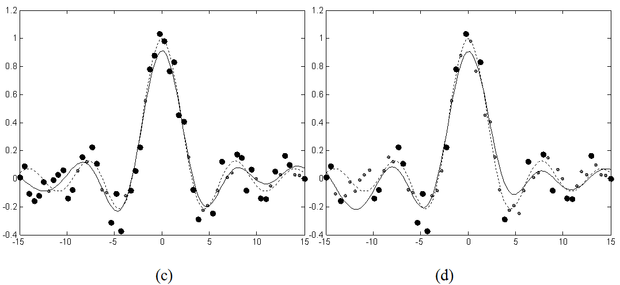
A 6.16 ábrasorozat az eljárás valós példán történő futtatásának eredményét mutatja. Az (a) ábrán az eredeti LS-SVM megoldása látható. A további ábrák az egyre nagyobb mértékű redukció eredményét mutatják: a (b), (c) és (d) ábrákon egyre több pontot hagytunk el az eredeti tanítókészletből, miközben az approximáció minősége jelentősen nem változott.

A négyzetes hibafüggvény a nem normál eloszlású zaj (például kilógó minták, „outlier”-ek) esetén nem optimális, ezért ilyen tanítómintáknál a modellt egy további módosítással hangolhatjuk. A módszer, hasonlóan a „pruning”-hoz az ${\alpha }_i=C{e}_i$ összefüggésen alapul. Ez az összefüggés azt mutatja, hogy az egyes pontokban kapott hiba, e_i arányos az eredményként kapott α_i súlyokkal. A módosított eljárás célja, hogy az egyes mintapontok szerepét a szerint mérlegelje, hogy ott mekkora a hiba. Ha e_i nagy, akkor az ehhez tartozó mintapont kevésbé megbízható, tehát a teljes eljárásban a szerepét célszerű csökkenteni, míg a pontosabb mintapontok szerepét, ahol e_i kisebb, érdemes növelni. Ezt a hatást egy újonnan bevezetett $v_i$ súlykészlettel érjük el. Az optimalizálandó egyenlet (a regressziós esetre felírva) ekkor a következőképpen módosul:

$\underset{w,b,e}{\text{min}}J\text{(}w,b,e\text{)}=\frac{1}{2}{w}^{T}w+C\frac{1}{2}{\displaystyle \sum _{i=1}^P{v}_i{e}_i^2}$ . (6.95)

A tanítópontokra vonatkozó feltételek nem változnak:

$d_i=w^T\phi \left(x_i\right)+b+e_i$ , $i=\mathrm{1,...,}P$ . (6.96)

A lineáris egyenletrendszerben ez a következőket jelenti:

$\left[\begin{array}{cc}0& {\overrightarrow{1}}^T\\ \overrightarrow{1}& \Omega +V_C\end{array}\right]\left[\begin{array}{c}b\\ \alpha \end{array}\right]=\left[\begin{array}{c}0\\ d\end{array}\right]$ (6.97)

ahol a $V_C$ az alábbi diagonál mátrix:

$V_C=\text{diag}\left(\left[\frac{1}{C{v}_1},\mathrm{...},\frac{1}{C{v}_P}\right]\right)$ (6.98)

A $v_i$ súlyokat az $e_i=\frac{{\alpha }_i}{C}$ értékek alapján választhatjuk meg, például a következők szerint:

$\begin{array}{ccc}{v}_i& =& \{\begin{array}{ccc}\begin{array}{l}1\\ \end{array}& \begin{array}{l}\text{ha}\\ \end{array}& \begin{array}{l}\left|e_i/s\right|\le c_1\\ \end{array}\\ \frac{c_2-\left|e_i/s\right|}{c_2-c_1}& \text{ha}& c_1\le \left|e_i/s\right|\le c_2\\ \begin{array}{l}\\ {10}^{-4}\end{array}& \begin{array}{l}\\ \text{egyébként}\end{array}& \end{array}\end{array}$ (6.99)

ahol c₁, c₂ és s megválasztása a statisztikában ismert módszerek alapján történhet [Suy02].

Az algoritmus menete a következő:

Ez az eljárás iteratívan ismételhető, de a gyakorlatban egy súlyozó lépés általában elegendő.

A tanítási sebesség növelésére, valamint a memóriaigények csökkentésére az LS-SVM lineáris egyenletrendszerét kell gyorsabban, kisebb memóriában megoldani. Erre Johan Suykens a Heistens-Stiefel konjugált gradiens módszert javasolja [Suy02]. Ez a lineáris egyenletrendszer egy iteratív megoldása, ami ez eredeti LS-SVM felírásnak megfelelő egyenletrendszer eredményére vezet.

Más lehetőség a ritka megoldás és a hatékonyság növelésének együttes alkalmazása, ami az LS-SVM módosítását jelenti. Ennek eléréséhez például a következőkben bemutatásra kerülő LS²-SVM-et vagy az LS-SVM-mel lényegében ekvivalens ridge regresszió egy redukált változatát, a csökkentett rangú kernel ridge regressziót alkalmazhatjuk.

Az új megközelítés kiindulópontja az LS-SVM lineáris egyenletrendszere. Ha a tanító készlet P mintapontot tartalmaz, akkor az egyenletrendszer $\text{(}P+1\text{)}$ ismeretlent, az $\alpha$ -kat és a b-t, $\text{(}P+1\text{)}$ egyenletet és ${\text{(}P+1\text{)}}^{\text{2}}$ együtthatót tartalmaz. Az együtthatók a $K\left(x_i,x_j\right)$ $i,j=\mathrm{1,...,}P$ kernel függvény értékek. A mintapontok száma tehát meghatározza az egyenletrendszer méretét, ami egyúttal a megoldás komplexitását, a hálózat méretét is megszabja. Hogy ritka megoldást, azaz egy kisebb modellt kapjunk, az egyenletrendszert, illetve az együtthatómátrix méretét redukálni kell.

Vizsgáljuk meg közelebbről az LS-SVM regressziós problémát leíró egyenletrendszert és jelentését. Az első sor jelentése:

${\displaystyle \sum _{k=1}^P{\alpha }_k}=0$ (6.100)

míg a j-edik sor a

$b+{\alpha }_{1}K\left(x_j,x_1\right)+\mathrm{...}+{\alpha }_k\left[K\left(x_j,x_k\right)+C^{-1}\right]+\mathrm{...}+{\alpha }_{P}K\left(x_j,x_P\right)=d_j$ (6.101)

feltételt, megkötést tartalmazza.

Az egyenletrendszer redukálásánál sorokat, illetve oszlopokat hagyhatunk el.

A fentiek alapján az egyenletrendszert leíró mátrix legfontosabb része a [ $\Omega +C^{-1}I$ ] részmátrix, ahol $\Omega$ az összes lehetséges tanítóvektor kombinációját tartalmazza ( ${\Omega }_{i,j}=K\text{(}{x}_i,x_j\text{)}$ ). A mátrix redukálása során abból sorokat, oszlopokat, illetve mindkettőt (sort a hozzá tartozó oszloppal) törölhetünk.

Minden oszlop egy neuronnak felel meg, míg a sorok bemenet-kimenet relációkat, azaz a megoldás által teljesítendő feltételeket fogalmaznak meg. A mátrix az alábbi két módon redukálható:

Az $\left(x_j,d_j\right)$ tanítópontot teljesen elhagyjuk, azaz mind a hozzá tartozó sort, mind pedig az oszlopot töröljük. Az alábbi egyenlet a tanító minták teljes elhagyásának hatását mutatja. A törölt elemeket szürkével jelöltük.

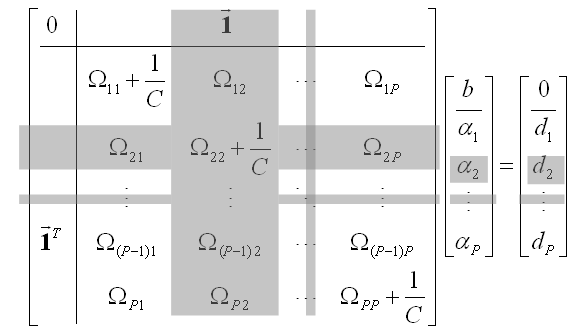(6.102)

A hagyományos metszési (pruning) technika esetében pontosan ez történik, hisz a metszési algoritmus iteratívan kihagyja a tanítópontok egy részét. Az elhagyott tanítópontok által hordozott információ ezért teljesen elvész. A tanítópontok által hordozott információ megőrzése a részleges redukció mellett lehetséges.

A $\left(x_j,d_j\right)$ tanító mintát csak részben hagyjuk el, úgy, hogy töröljük a ponthoz tartozó oszlopot, de megtartjuk a hozzá tartozó sort. Így a tanítóminta által hordozott megkötés továbbra is érvényben marad, hisz az adott sor súlyozott összegének amennyire csak lehet egyezni kell a $d_j$ kívánt kimenettel .

Ha kiválasztunk $M$ ( $M<P$ ) “szupport vektort” (oszlopot), de megtartjuk az összes megkötést (sort), az egyenletrendszer túlhatározottá válik. A részleges redukció hatását a mutatja a következő összefüggés, ahol a szürkével jelölt részeket távolítjuk el.

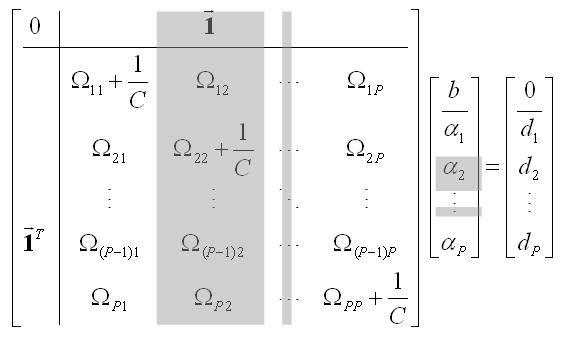(6.103)

A fentiek alapján kapott túlhatározott ( $P\times M$ méretű) egyenletrendszert legkisebb négyzetes hiba értelemben oldhatjuk meg. Egyszerűsítsük a jelöléseinket úgy, hogy a fenti egyenletrendszer mátrix alakja legyen:

$$ $Au=v$ , (6.104)

melynek legkisebb négyzetes hibájú megoldása:

$u={\left(A^{T}A\right)}^{-1}{A}^{T}v$ . (6.105)

Az oszlopok törlése a sorok megtartása mellet biztosítja, hogy a kernelek (neuronok) száma csökkenjen, miközben az eljárás az összes ismert megkötést (tanítómintát) figyelembe veszi. Ez a kulcsa annak, hogy a modell komplexitása a pontosság megtartása mellett is csökkenthető legyen.

Látható, hogy a kernel mátrix redukciója során az oszlopok elhagyásával a regularizálás „aszimmetrikussá” válik, hiszen a továbbiakban nem minden sorban szerepel regularizáció. Ennek kiküszöbölésére megtehető, hogy a regularizációt már csak a kernel térbeli megoldás során használjuk, ami a kernel térbeli margó maximalizálásnak ( $\Vert \alpha \Vert$ minimalizálásának) felel meg. Ez hasonló az SV megoldások nemlineáris kiterjesztéséhez, ahol a w súlyvektor minimalizálása valójában a jellemző térben történik. A kernel térben regularizált megoldás:

$\text{(}{A}^{T}A+C^{-1}I\text{)}u=A^{T}v$ , (6.106)

ahol

$A=\left[\begin{array}{cc}0& 1^T\\ 1& \Omega \end{array}\right]$ , $\Omega =\left[\begin{array}{ccc}K\text{(}{x}_1,x_1\text{)}& \cdots & K\text{(}{x}_1,x_M\text{)}\\ & & \\ ⋮& \ddots & ⋮\\ & & \\ K\text{(}{x}_P,x_1\text{)}& \cdots & K\text{(}{x}_P,x_M\text{)}\end{array}\right]$ . (6.107)

A módosított, részlegesen redukált egyenletrendszert legkisebb négyzetes hibájú (least-squares) értelemben oldjuk meg, ezért nevezzük ezt a módszert Least Squares LS-SVM-nek vagy röviden LS²-SVM-nek [Val04].

Az itt bemutatott részleges redukció hasonlít a hagyományos SVM kiterjesztéseként bevezetett redukált szupport vektor gép (Reduced Support Vector Machine − RSVM) alapelvéhez [Lee01b]. Az RSVM esetén azonban, mivel az SVM eleve kisebb (ritka) modellt eredményez, a részleges redukció célja az algoritmikus komplexitás csökkentése, míg az LS-SVM esetében elsődlegesen a modell komplexitásának, a hálózat méretének csökkentése, azaz a ritka LS-SVM elérése a cél.

A fenti részleges redukció alkalmazása esetén szükség van valamilyen módszerre, ami meghatározza a szükséges szupport vektorokat. A kernel mátrix oszlopaiból kiválasztható egy lineárisan független részhalmaz, melynek elemeiből lineáris kombinációival a többi előállítható. Ez a kernel mátrix „bázisának” meghatározásával érhető el, hiszen az oszlopvektorok terének bázisa az a legkisebb vektorkészlet, amellyel a feladat megoldható. Ha a bázis meghatározásánál nem követeljük meg, hogy az oszlopvektorok által kifeszített tér és a kiválasztott bázisok által kifeszített tér azonos legyen, hanem bizonyos toleranciát is megengedünk, akkor a tolerancia mértékének meghatározásával egy szabad paramétert kaptunk. Ez a szabad paraméter lehetővé teszi, hogy kontroláljuk a bázisvektorok számát (M), hiszen a célunk az, hogy a P darab P-dimenziós oszlopvektorból M<P bázisvektort határozzunk meg, ahol M minél kisebb.

A bázisvektorok száma, ami egyben a szupport vektorok száma is, valójában nem függ a mintapontok számától (P), csak a probléma nehézségétől, hiszen M a mátrix lineárisan független oszlopainak száma. A gyakorlatban ez azt jelenti, hogy ha egy probléma nehézsége M neuront igényel, akkor a tanításhoz felhasznált mintapontok számától függetlenül a modell mérete nem növekszik.

A szupport vektorok kiválasztása az $A^T$ mátrix RRE alakra (reduced row echelon form, RREF) hozása során részleges pivotolással végrehajtott Gauss-Jordan eliminációval történik [Pre02], [Gol89b] (ld. Függelék). A tolerancia figyelembevétele a pivot elem (p) ellenőrzésével lehetséges. Eredetileg a pivotolás lényege, hogy az elimináció végrehajtása során szükséges osztásban a lehető legnagyobb elemet használjuk fel a numerikus stabilitás érdekében. A kiválasztott pivot elem nagysága azonban információt hordoz arról is, hogy mennyire fontos a hozzá tartozó oszlop a pontos megoldáshoz. Ha $p\le {\epsilon }^{\prime }$ (ahol ε’ a tolerancia paraméter), akkor az adott oszlop elhagyható, ellenkező esetben az oszlopnak megfelelő bemenet egy szupport vektor. A módszer azon oszlopvektorok listáját adja meg, melyek az ε’ toleranciaérték értelmében lineárisan függetlenek.

A megfelelő tolerancia helyes meghatározása hasonló a többi hiperparaméter (C, ε, valamint a kernel paraméterek) megválasztásához. Egy lehetséges megoldás a kereszt kiértékelés (cross-validation) alkalmazása. Minél nagyobb a tolerancia, annál kisebb a hálózat, és annál nagyobb az approximáció hibája. Az ε’ helyes megválasztása egy olyan kompromisszum alapján lehetséges, ahol a pontos approximáció, illetve a modell komplexitása áll szemben egymással.

A 6.17 ábra zajos mintapontok mellett mutatja az LS²-SVM eredményét. Fontos hangsúlyozni, hogy nulla tolerancia esetén az LS²-SVM és az LS-SVM megoldás azonos, mivel ebben az esetben a kiválasztási módszer a mátrix minden oszlopát, azaz az összes tanítómintát megtartja (kivéve, ha a tanítópontok között volt redundancia).

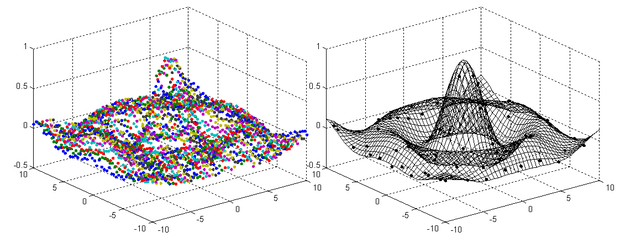
Az alábbiakban az LS²-SVM alkalmazására mutatunk két mintapéldát. A 6.18 ábrán egy kétdimenziós sinc függvény LS²-SVM-mel történő approximációja látható. A bal oldali ábra a kiinduló tanítópontokat mutatja, a jobboldali pedig a megoldást, ahol külön megjelennek az eljárás által meghagyott tanítópontok (szupport vektorok) is. Láthatóan a tanítópontok elenyésző töredéke elég a megfelelően pontos approximáció eléréséhez. A 6.19 ábra a klasszikus kettős spirál probléma megoldását adja meg. A módszer hatékonyságnövelő hatása itt is jól követhető.

Az LS-SVM-nél megmutattuk, hogy egy iteratív eljárással súlyozott megoldás is adható, ami zajos esetben, főként kilógó minták (outlierek) esetén jelentősen jobb megoldásra vezet.

Amennyiben ismert vagy becsülhető a tanító mintákat terhelő zaj mértéke, ezt az információt az LS²-SVM esetén is fel lehet használni. A mintapontok azonos kezelése helyett ebben az esetben a pontosabb mintákat nagyobb, a pontatlan, azaz zajos mintákat kisebb súllyal célszerű figyelembe venni. A hiba súlyozott számítása:

${\epsilon }_v=\text{}{\displaystyle \sum _{i=1}^P{v}_i{e}_{{}^i}^2}=\text{}{\displaystyle \sum _{i=1}^P{v}_i{\text{(}{d}_i-y_i\text{)}}^2}$ (6.108)

A túlhatározott LS²-SVM egyenletrendszer súlyozott megoldása az előbbiekben bevezetett átírást alkalmazva:

$A^{T}VAu=A^{T}Vv$ , (6.109)

ahol a V súlyozó mátrix egy diagonálmátrix, amely a főátlóban a $v_i$ súlyokat tartalmazza. A súlyokat úgy kell beállítani, hogy jól tükrözzék az egyes tanítóminták hatását a lineáris illesztésre. A zaj mértéke, illetve a súlyozás meghatározható egy előzetes megoldás alapján (vagy a priori információ alapján), de a túlhatározott egyenletrendszer megoldására használhatunk olyan statisztikai megoldó módszereket is, amelyek csökkentik a nagyon hibás adatok hatását. Ilyen például a Least Absolute Residuals – LAR, a Bisquare weights vagy a Least Trimmed Squares - (LTS) módszer [Ciz04], [Hol77], [Hub81].

A korábban bemutatott osztályozási problémának megfelelően itt is az ${\left\{x_i,d_i\right\}}_{i=1}^P$ tanító mintakészlet alapján keressük az $y\text{(}x\text{)}=x^{T}w$ lineáris modellt. A ridge regresszió is a négyzetes hibát minimalizálja, de az LS-SVM-hez hasonlóan közben a súlyvektor hosszának minimumát is biztosítani szeretné, ami regressziós feladatoknál a minél laposabb megoldást biztosítja [Sch02]. Ennek megfelelően a $w\in R^N$ súlyvektort ridge regresszióval a következőképpen határozzuk meg. Jelölje J(w) most is a minimalizálandó kritériumfüggvényt (az 1/2-es szorzó a deriválás utáni eredmény egyszerűsítése miatt szerepel):

$J\text{(}w\text{)}=\frac{1}{2}{\Vert w\Vert }_{}^2+\frac{1}{2}C{\displaystyle \sum _{i=1}^P{\text{(}{d}_i-x_i^{T}w\text{)}}^2}$ (6.113)

A $\frac{\partial J}{\partial w}$ parciális deriválás eredményéből az optimális w az alábbiak szerint számítható:

${\displaystyle \sum _{i=1}^P\text{(}{d}_i-x_i^{T}w\text{)}{x}_i}=\frac{\text{1}}{C}w$ (6.114)

$w={\left({\displaystyle \sum _{i=1}^P{x}_i{x}_i^T+}\frac{\text{1}}{C}I\right)}^{-1}\left({\displaystyle \sum _{j=1}^P{d}_j{x}_j}\right)$ (6.115)

Mátrix alakban felírva (ahol $d={\begin{array}{ccc}\text{[}{d}_1& \dots & d_P\text{]}\end{array}}^T$ a tanítópontok kívánt válaszaiból képezett vektor és X az $x_i$ $i=\mathrm{1...}P$ tanítóminta-bemenetekből, mint sorvektorokból képezett mátrix):

$X=\left[\begin{array}{c}{x}_1{}^T\\ x_2{}^T\\ ⋮\\ x_P{}^T\end{array}\right]$ , (6.116)

a megoldás súlyvektor:

$w={\left(X^{T}X+\frac{\text{1}}{C}I\right)}^{-1}{X}^{T}d=X^T{\left(X{X}^T+\frac{\text{1}}{C}I\right)}^{-1}d$ . (6.117)

Az

$\alpha ={\left(X{X}_{}^T+\frac{\text{1}}{C}I\right)}^{-1}d$ (6.118)

jelölés bevezetésével

$w=X^T\alpha$ (6.119)

így a végeredmény:

$y\text{(}x\text{)}=x_{}^T{X}^T\alpha ={\displaystyle \sum _{i=1}^P{\alpha }_i{x}_{}^T{x}_i}$ (6.120)

Vegyük észre, hogy ez a felírás egy kis különbséggel megegyezik a 6.1 részben bevezetett egyszerű kernel gép összefüggéseivel. A kis különbség abból adódik, hogy itt a kiinduló kritériumfüggvény a súlyvektor hosszának négyzetét, mint minimalizálandó mennyiséget, is tartalmazza. Ennek következménye a w illetve az $\alpha$ vektorok összefüggéseiben ((6.117), illetve (6.118) összefüggések) a $C^{-1}I$ regularizációs tag megjelenése. A ridge regresszió tehát az egyszerű kernel gép regularizált változata. Azt is észrevehetjük, hogy ez az eredmény megegyezik az eltolás-érték nélküli lineáris LS-SVM-re kapott összefüggéssel.

Természetesen a ridge regresszió is kiterjeszthető nemlineáris esetre a szokásos $\phi \left(x\right)$ transzformáció, és a kernel trükk alkalmazásával.

A nemlineáris ridge regresszió esetén – csakúgy, mint az SVM vagy az LS-SVM kiterjesztésénél – a lineáris regressziós modellt egy magasabb dimenziós térben, a jellemző térben alkalmazzuk, ami a szokásos módon egy nemlineáris transzformáció eredménye.

A ϕ(.) leképezés segítségével a lineáris esetben megismert célfüggvény a következőképpen módosul:

$J\text{(}w\text{)}=\frac{1}{2}{\Vert w\Vert }_{}^2+\frac{1}{2}C{\displaystyle \sum _{i=1}^P{e}_i^2}$ (6.121)

ahol:

$e_i^{}=d_i-w^T\phi (x_i)$ , $i=\mathrm{1,...,}P$ . (6.122)

Az LS-SVM regressziónál bemutatott lépéseknek megfelelően az $L(w,e,\alpha )$ Lagrange-függvény írható fel az ${\alpha }_i$ ( $i=\mathrm{1,...,}P$ ) Lagrange együtthatókkal. A deriválások után a kernel trükk alkalmazásával az alábbi megoldás nyerhető (mátrix alakban):

$\alpha ={\text{(}\Omega +\frac{1}{C}I\text{)}}^{-1}d$ , (6.123)

ahol az ${\Omega }_{i,j}=K(x_i,x_j)$ a tanítómintákból képzett kernel mátrix. Látható, hogy a nemlineáris eset itt is a kernel térben kerül megoldásra. A megoldás ugyanakkor megfelel egy regularizált kernel térbeli megoldásnak. Ez annyit tesz, hogy a ${\Vert w\Vert }_{}^2$ jellemzőtérbeli minimalizálása az ${\Vert \alpha \Vert }^2$ kernel térbeli minimalizálására vezet.

A kernel ridge regressziós modell:

$y\text{(}x\text{)}={\displaystyle \sum _{i=1}^P{\alpha }_{i}K\text{(}x,x_i\text{)}}$ , (6.124)

ami a regularizációtól eltekintve ismét megegyezik az egyszerű nemlineáris kernel gép válaszával (ld. (6.14) összefüggés).

Az eredeti ridge regressziós megoldásokban a kernel mátrix négyzetes, ami azt jelenti, hogy a modell a tanító pontoknak megfelelő számú szupport vektort tartalmaz, azaz nem ritka. A csökkentett rangú kernel ridge regresszió (Reduced Rank Kernel Ridge Regression - RRKRR) [Caw02] eljárás a ritka megoldást a kernel mátrix redukciójával éri el. Az RRKRR eljárás tehát hasonló célt tűz ki, mint az LS²-SVM, a célhoz azonban más úton jut el.

Az eljárást eltolásérték (bias) alkalmazása mellett mutatjuk be, hogy az eredmény összevethető legyen az LS-SVM eredményével.

A ritka megoldáshoz az approximációban felhasznált kernel függvények – azaz a kernel középpon-toknak megfelelő szupport vektorok – számát kell csökkenteni. Az eredeti ridge regresszió (és természetesen az LS-SVM is) olyan kernel mátrixot használ fel, ahol mind az oszlopok, mind a sorok számát a tanítópontok száma határozza meg, hiszen minden tanítópont egy kernel középpont – ezek felelnek meg az oszlopoknak – és ugyanakkor minden tanítópont a jellemzőtérben egy lineáris egyenletet is jelent – ezek felelnek meg a soroknak. Az RRKRR eljárás az oszlopok számát redukálja úgy, hogy a tanítópontokból kiválaszt egy részhalmazt – ezek fogják képezni a kernel középpontokat –, és megtartja az összes tanítópontot, tehát megtartja a sorok számát. Az RRKRR eljárás tehát az LS²-SVM-hez hasonlóan részleges redukciót alkalmaz.

Az oszlopok kiválogatásához az alábbiakból indulhatunk ki. Az LS-SVM (6.83) és (6.91) összefüggései a w súlyvektort, mint a $\phi (x_i)$ jellemzőtérbeli vektorok súlyozott összegét fejezik ki.:

$w={\displaystyle \sum _{i=1}^P{\alpha }_i\phi \text{(}{x}_i\text{)}}$ (6.125)

Ez azt jelenti, hogy a súlyvektorok terét a $\phi \text{(}{x}_i\text{)}$ vektorok meghatározzák; mint bázisvektorok kifeszítik a teret. Kérdés azonban, hogy az összes $\phi \text{(}{x}_i\text{)}$ , i=1,…,P jellemzőtérbeli vektorra szükség van-e a súlyvektor (adott pontosságú) reprezentációjához. Tételezzük fel, hogy ehhez a tanítópontok egy S részhalmaza elegendő. Ekkor a w súlyvektor felírható az S részhalmazba tartozó jellemzővektorok súlyozott összegeként:

$w={\displaystyle \sum _{i\in S}{\beta }_i\phi (x_i)}$ . (6.126)

Ha ez a megadás pontos, akkor az S-be tartozó $\phi \text{(}{x}_i\text{)}$ vektorok is kifeszítik a súlyvektorok terét, tehát bázist alkotnak ebben a térben. Ha S elemeinek száma kisebb, mint P, eredményként ritka megoldást kapunk. Természetesen itt a β_i súlyok különbözni fognak az (6.125) szerinti megadás α _i súlyaitól.

Ha az S részhalmazba tartozó jellemzővektorok bázist alkotnak a jellemzőtérben, akkor bármely x bemenet jellemzőtérbeli képe is kifejezhető, mint az S-beli $\phi \text{(}{x}_i\text{)}$ vektorok lineáris kombinációja.

$\phi \text{(}x\text{)}={\displaystyle \sum _{i\in S}{\zeta }_i\phi \text{(}{x}_i\text{)}}$ . (6.127)

Ha a bázisvektorok $\phi \text{(}x\text{)}$ -nek csak közelítő reprezentációját, ${\widehat{\phi }}_S\text{(}x\text{)}$ -et adják, akkor olyan bázisfüggvényeket kell kiválasztanunk, melyek mellett ez a közelítés a legkisebb hibájú. A hibát most mint a két vektor normalizált euklideszi távolságát definiálhatjuk:

${\delta }_j=\frac{{\Vert \phi \text{(}{x}_j\text{)-}{\widehat{\phi }}_S\text{(}{x}_j\text{)}\Vert }^2}{{\Vert \phi \text{(}{x}_j\text{)}\Vert }^2}$ . (6.128)

Megmutatható [Bau01], hogy ez a hiba a kernel trükk felhasználásával a kernel mátrix segítségével is felírható:

${\delta }_j=1-\frac{K_{Sj}^T{K}_{SS}^{-1}{K}_{Sj}^{}}{k_{jj}}$ . (6.129)

ahol $K_{SS}^{}$ a K kernel mátrix almátrixa: $K_{SS}^{}={\left\{K_{ij}\right\}}_{i,j\in S}^{}$ , $K_{Sj}^{}={\left\{K_{ji}\right\}}_{j\in S}^T$ pedig egy belső szorzatokból képezett oszlopvektor, míg k_jj = K_jj, a kernel mátrix j-edik főátlóbeli eleme.

A jellemzőtér bázisának meghatározásához az így definiált hiba átlagát kell minimalizálni a tanítókészlet összes pontját tekintetbe véve. Vagyis maximalizálni kell a

$J\text{(}S\text{)}=\frac{1}{P}{\displaystyle \sum _{j=1}^P\frac{K_{Sj}^T{K}_{SS}^{-1}{K}_{Sj}^{}}{k_{jj}}}$ (6.130)

mennyiséget. Az eljárást az üres halmazzal, vagyis $S=\varnothing$ -val indítjuk, és mohó stratégiát alkalmazunk. Minden egyes lépésben azt a tanítóvektort adjuk S–hez, mely a (6.130) kifejezést maximálja. Az eljárás magától leáll, ha $K_{SS}^{}$ már nem invertálható, jelezve, hogy a megfeleleő bázist megtaláltuk, illetve leállítható, ha a hiba adott korlát alá csökken vagy egy előre meghatározott számú bázisvektort már kiválasztottunk.

Mivel a súlyvektor (6.126) szerint kifejezhető S-be tartozó bázisvektorok lineáris kombinációjaként, a következő duális egyenletet kapjuk, melyet $\beta$ és b szerint kell minimalizálnunk.

$J\text{(}\beta ,b\text{)}=\frac{1}{2}{\displaystyle \sum _{i,j\in S}{\beta }_i{\beta }_{j}K\text{(}{x}_i,x_j\text{)}}+\frac{1}{2}C{\displaystyle \sum _{i=1}^P{\text{(}{d}_i-{\displaystyle \sum _{j\in S}{\beta }_{j}K\text{(}{x}_i,x_j\text{)}}-b\text{)}}^2}$ . (6.131)

A $\beta$ és $b$ szerinti parciális deriváltak alapján megkeresve a minimumhelyeket, valamint ezt C-vel leosztva az alábbi egyenletet kapjuk:

${\displaystyle \sum _{i\in S}{\beta }_i{\displaystyle \sum _{j=1}^{P}K\text{(}{x}_i,x_j\text{)}}}+b={\displaystyle \sum _{j=1}^P{d}_j}$ (6.132)

és $\forall r\in S-\text{re}$

$\begin{array}{l}{\displaystyle \sum _{i\in S}{\beta }_i\left(\frac{1}{C}K\text{(}{x}_i,x_r\text{)}+{\displaystyle \sum _{j=1}^{P}K\text{(}{x}_j,x_r\text{)}K\text{(}{x}_j,x_i\text{)}}\right)}+b{\displaystyle \sum _{i=1}^{P}K\text{(}{x}_i,x_r\text{)}}=\\ ={\displaystyle \sum _{j=1}^P{d}_{j}K\text{(}{x}_i,x_r\text{)}}\end{array}$ (6.133)

A fenti egyenletek az alábbi $\text{(}\left|S\right|+1\text{)}\times \text{(}\left|S\right|+1\text{)}$ méretű lineáris egyenletrendszerre vezetnek ( $\left|S\right|$ az S halmaz elemeinek a száma):

$\left[\begin{array}{cc}\Omega & \Phi \\ \Phi & P\end{array}\right]\left[\begin{array}{c}\beta \\ b\end{array}\right]=\left[\begin{array}{c}c\\ {\displaystyle {\sum }_{i=1}^P{d}_i}\end{array}\right]$ , (6.134)

ahol

${\Omega }_{r,i}=\frac{1}{C}K\text{(}{x}_i,x_r\text{)}+{\displaystyle \sum _{j=1}^{P}K\text{(}{x}_j,x_r\text{)}K\text{(}{x}_j,x_i\text{)}}$ , $i,r\in S$

${\Phi }_r={\displaystyle \sum _{i=1}^{P}K\text{(}{x}_i,x_r\text{)}}$ , $\forall i\in S$

c pedig egy olyan $\left|S\right|$ -dimenziós vektor, melynek r-edik eleme:

$c_r={\displaystyle \sum _{j=1}^P{d}_{j}K\text{(}{x}_i,x_r\text{)}}$ $\forall i\in S$

Az egyenletrendszer megoldása egy csökkentett rangú (bázisú) ritka megoldásra vezet, mivel az csak $\left|S\right|$ számú kernelt és az eltolást tartalmazza.