Az előzőekben bemutatott egyszerű kernel gép arra adott példát, hogy az 5. fejezetben bemutatott bázisfüggvényes hálók kernel gépként is értelmezhetők. Ennél az értelmezésnél a probléma megfogalmazása nem változott az eredeti bázisfüggvényes megfogalmazáshoz képest: mindkét esetben az átlagos négyzetes hiba minimumát biztosító megoldásra törekedtünk.
Kernel gépek azonban más megközelítésből is konstruálhatók. A Bernhard Boser, Isabel Guyon és Vladimir Vapnik által javasolt szupport vektor gép [Bos92 ] talán a legfontosabb, több új szempontot is hozó kernel gépnek tekinthető. A szupport vektor gépek olyan kernel gépek, melyek a statisztikus tanuláselmélet eredményeit is hasznosítják. Alapváltozatuk lineáris szeparálásra képes, amely azonban kiterjeszthető nemlineáris szeparálásra és nemlineáris regressziós feladatokra is.
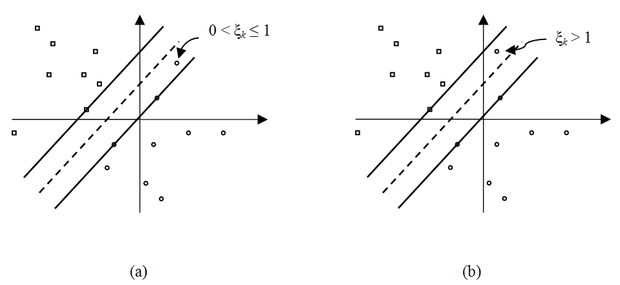
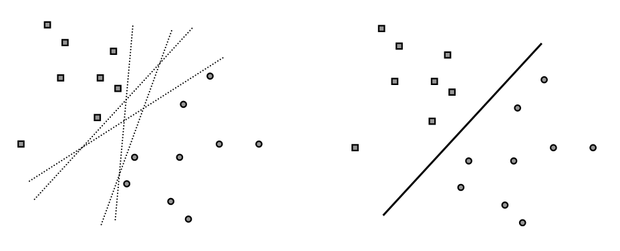
Amint azt korábban láttuk, a lineáris szeparálási feladat megoldható egy egyszerű perceptronnal. A Rosenblatt perceptron azonban egy lineárisan szeparálható feladat egy lehetséges megoldását adja, miközben tudjuk, hogy lineárisan szeparálható mintapontok esetében általában végtelen sok különböző megoldásunk lehet. Ezek a megoldások egyenértékűek abból a szempontból, hogy mindegyikük egy olyan lineáris elválasztó felületet határoz meg, amely a tanítópontokat hibátlanul szétválasztja. A szeparálás minősége azonban az egyes megoldásokban mégis jelentősen különbözhet. Ezt illusztrálja a 6.2 ábra.
Bár az ábra bal oldali részén látható összes egyenes hibátlanul szétválasztja a tanítópontokat, az a sejtésünk, hogy a jobb oldalon látható folytonos vonallal rajzolt egyenes kitüntetett a lehetséges megoldások között. A mintapontokból történő tanulásnál ugyanis nemcsak a tanítópontok megtanulására törekszünk, hanem megfelelő általánosítóképesség elérésére is. A mintapontok valamilyen − számunkra általában ismeretlen − eloszlású mintahalmazokból származnak, és a feladat nemcsak a véges számú ismert válaszú tanítópont helyes osztályozása, hanem az egész osztályozási feladat minél jobb megoldása is. Feltételezve, hogy a tanítópontok kellően reprezentálják a megoldandó problémát, azt várjuk, hogy az az elválasztás eredményez jobb általánosítóképességet, amely a két osztályba tartozó tanítópontok között, a tanítópontoktól a lehető legnagyobb távolságra helyezkedik el. A lineáris kétosztályos osztályozási feladat megoldását adó szupport vektor gép ezt az „optimális” elválasztó felületet határozza meg.
A következőkben előbb ezt a legegyszerűbb esetet és a megfelelő megoldást mutatjuk be, majd a szupport vektor gépeket kiterjesztjük lineárisan nem megoldható osztályozási, végül nemlineáris regressziósfeladatok megoldására is.
6.3.1. Lineárisan szeparálható feladat lineáris megoldása
Fentiek értelmében optimális lineáris szeparálásnak azt a megoldást tekintjük, amikor az elválasztó egyenes (sík, hipersík) a két osztályba tartozó tanítópontok között a pontoktól a lehető legnagyobb távolságra helyezkedik el. A pontok között középre elhelyezett szeparáló felületet a tanítópontoktól egy margó (margin), azaz egy biztonsági sáv választja el, ezért az így megoldható feladatokat maximális tartalékot vagy maximális margót biztosító lineárisan szeparálható osztályozási feladatoknak is nevezzük. A következőkben ennek a feladatnak a megoldását mutatjuk be.
Legyenek adottak az
tanítópontok, ahol az
N-dimenziós bemeneti pontok két osztály valamelyikéből származhatnak, vagyis a kívánt válaszok a két lehetséges érték egyikét veszik fel:
. Egy olyan
szeparáló függvényt keresünk, amely a tanítópontokat hiba nélkül osztályozza:
i=1,2,…, P (6.23)
továbbá, ahol a hipersíkhoz legközelebb álló tanítópontoknak a síktól vett távolsága maximális.
A (6.23) egyenlőtlenségben a valamilyen kis pozitív konstans, di pedig az xi-hez tartozó kívánt
válasz.
A hipersík paramétereinek megfelelő skálázásával biztosítható, hogy
(6.24)
legyen, vagyis a síkhoz legközelebb eső pontokban az elválasztó függvény abszolút értéke 1 legyen. Így a feladat az alábbi tömörebb formában is felírható:
(6.25)
Jelölje az optimális szeparáló lineáris felület paramétereit
és
, és határozzuk meg egy x pontnak ettől a hipersíktól való távolságát. A 6.3 ábrát követve jelölje
az
pont merőleges vetületét a szeparáló felületre. Ekkor a pont felírható a vetület és a szeparáló felület normálvektora segítségével:
. (6.26)
Mivel
,
, vagyis az x pontnak az optimális szeparáló hipersíktól való távolságára
(6.27)
adódik, ahol
a
vektor euklideszi normáját jelöli. Az optimális hipersík a síkhoz legközelebbi tanítópontok távolságának maximumát biztosítja.
Az egységnyi távolságúra skálázott feladatban a határoló felülethez legközelebb eső pontokra
vagy
. Ekkor a szeparáló hipersíkhoz legközelebb eső, különböző osztályba tartozó bemeneti vektorok közötti, a síkra merőlegesen mért távolság
. (6.28)
Az optimális hipersík által biztosított margó tehát:
. (6.29)
Az egyenlet szerint az osztályozási tartalék akkor lesz maximális, ha
minimális értékű.
A megoldandó feladat ezek után a következőképpen fogalmazható meg: adott egy lineárisan szeparálható mintapont készlet
, (6.30)
és keressük azt a minimális normájú w* vektort és azt a b* skalár értéket, melyekkel a tanítópontok mindegyikét helyesen osztályozzuk, vagyis keressük a
(6.31)
megoldását, azzal a feltételellel, hogy
. (6.32)
A feladatot tehát feltételes szélsőérték-keresési problémaként tudjuk megfogalmazni, ahol a feltételek egyenlőtlenségek formájában vannak megadva. A feltételes szélsőérték-keresési feladat megoldását egy Lagrange kritérium (ld. Függelék) megoldásával kereshetjük:
, (6.33)
ahol az
együtthatók a Lagrange multiplikátorok. Az optimalizálási feladatnak ezt a felírását elsődleges alaknak (primal problem) nevezzük.
A optimalizálási feladat megoldásához a Karush-Kuhn-Tucker (KKT) elmélet (ld. Függelék) szerint a fenti Lagrange kritériumot kell minimalizálni
és
szerint és maximalizálni
szerint, vagyis a Lagrange kritérium által definiált kritériumfelület nyeregpontját (saddle point) kell meghatározni. A megoldás két lépesben érhető el:
-
először w és b szerinti szélsőértéket keresünk a megfelelő deriváltak számításával,
-
majd ezek eredményét behelyettesítve a Lagrange kritériumba kapjuk az ún. másodlagos feladatot (dual problem), melynek megoldásai az
•
• Lagrange multiplikátorok.
Az
Lagrange kritérium
és
szerinti parciális deriválásából az optimumra az alábbi két feltételt kapjuk:
, (6.34)
(6.35)
Látható, hogy ha a Lagrange multiplikárokat ismerjük, a feladatot megoldottuk, hiszen
csak az
Lagrange multiplikátoroktól és a tanítópont-értékektől függ.
A feltételes optimalizálási feladat megoldásához felírható annak duális alakja, melyben már csak az
Lagrange multiplikátorok az ismeretlenek. Mivel az
(6.36)
kifejtésében a harmadik tag (1.35) alapján nulla, és mivel (6.34) alapján
(6.37)
az
duális optimalizálási feladat az alábbi:
(6.38)
a
(6.39)
és a
,
(6.40)
feltételekkel.
A duális probléma egy olyan, a keresett
értékekben másodfokú szélsőérték-keresési feladat, mely mellett a megoldásnak egy egyenlőség, (6.39) és egy egyenlőtlenség, (6.40) típusú mellékfeltételt is ki kell elégítenie. Az ilyen típusú optimalizálási feladatok kvadratikus programozással (quadratic programming, QP) oldhatók meg. Az optimumhoz tartozó Lagrange multiplikátorok – az
értékek – ismeretében, felhasználva az optimális súlyvektorra vonatkozó (6.34) összefüggést, a lineáris kétosztályos osztályozó szupport vektor gép válasza felírható, mint
. (6.41)
Vegyük észre, hogy a válasz összefüggésében a bemeneti mintavektorok nem közvetlenül, hanem egy skalár szorzat részeként szerepelnek, tehát a (1.11) összefüggéshez hasonlóan itt is kernel megoldást kaptunk. A megoldás érdekessége, hogy az
-k nagyrésze általában 0, így mind a súlyvektor kifejezésében, mind a szupport vektor gép válaszában a tanítópontoknak csak egy része – a P tanítópontból csak Ps – vesz részt.
Azokat a tanítópontokat, amelyek résztvesznek a megoldás kialakításában, amelyekhez tartozó Lagrange multiplikátorok értéke nem nulla, szupport vektoroknak (support vectors) nevezzük.[] A szupport vektor gépek tehát olyan kernel gépek, ahol a kernel tér tényleges dimenziója nem a tanítópontok számával (P), hanem a szupport vektorok számával (Ps) egyezik meg. Ez jelentős egyszerűsítést jelenthet a válasz számításában, különösen, ha Ps<<P. A szupport vektor gépeknek ezt a tulajdonságát ritkasági (sparseness) tulajdonságnak nevezzük.
Azt is észrevehetjük, hogy azon tanitópontokra, ahol
, teljesül a
(6.42)
összefüggés, vagyis ezek a tanitópontok – tehát a szupport vektorok – lesznek az elválasztó hipersíkhoz legközelebb lévő mintapontok. Itt w* már az optimális Lagrange együtthatókkal meghatározható súlyvektor:
, (6.43)
A szupport vektoroknál (6.42) alapján a (6.24) és a (6.25) egyenlőtlenségek egyenlőségként állnak fenn. Az optimális eltolásérték (bias) (
) a
egyenletből számítható, ahol
egy szupport vektor.
A maximális margójú lineáris szeparálás általánosítóképessége
Az előzőekben láttuk, hogy egy tanuló rendszer létrehozásánál a konstrukciós lépések meghatározásán túl fontos kérdés, hogy a létrehozott rendszert minősíteni is tudjuk. A 3. fejezetben részletesebben tárgyaltuk a minősítés lehetőségeit és bemutattuk, hogy a minősítéshez valójában az ún. valódi kockázat meghatározására lenne szükség. Azt is láttuk, hogy a valódi kockázatot – a mintapont-eloszlás ismeretének hiányában – nem tudjuk meghatározni. A statisztikus tanuláselmélet azonban megadja azokat a feltételeket, melyek fennállta esetén a valódi kockázatnak legalább egy felső korlátja megadható.
A (2.31) összefüggés osztályozási feladatra adott felső korlátot. A felső korlát két tagból állt: egyrészt a tanítópontokban meghatározható eredő hibából, a tapasztalati kockázatból, és egy ún. konfidencia tagból, ami a megoldás komplexitásától függ. A statisztikus tanuláselmélet a komplexitás mértékeként a VC-dimenziót használja. Ha tehát egy megoldás VC-dimenziójára tudunk mondani valamit, a valódi kockázat egy felső korlátja megadható. A felső korlát (2.31) összefüggése alapján azt is láttuk, hogy olyan megoldásra van szükségünk, amely egyidejűleg mindkét tagot minimalizálja, tehát a tapasztalati hibát úgy próbálja minél kisebbre leszorítani, hogy közben a VC-dimenzió értéke is minél kisebb legyen. A megoldás elve a strukturális kockázat minimalizálás (SRM) elv volt. A strukturális kockázat minimalizálás elve szerint azt a legkevésbé komplex megoldást keressük, melynél a két tag összege minimumot ad.
A lineáris osztályozó szupport vektor gépnél, azon túl, hogy a tanítópontok hibátlan osztályozását kívánjuk elérni, még azt is célnak tekintjük, hogy a szeparálás maximális biztonsággal, maximális margó mellett történjen meg. A maximális margójú megoldás a lineáris szeparálások között kitüntetett. A maximális margó biztosítása mellett ugyanis a megoldás komplexitásának mértékére, a VC-dimenzióra is adható egy felső korlát, és ennek segítségével a lineáris szupport vektor gép általánosítóképességéről is tudunk állítani valamit.
A statisztikus tanuláselmélet eredményei szerint [Vap95], [Vap98] a
(6.44)
által megadott optimális szeparáló hipersík VC-dimenziójára az alábbi felső korlát adható:
(6.45)
ahol N a bemeneti tér dimenziója, r a szeparációs tartalék, a margó,
pedig az összes bemeneti vektort tartalmazó legkisebb átmérőjű gömb sugara. Az összefüggésben a
művelet azt a legkisebb egészet jelöli, ami nagyobb vagy egyenlő, mint a művelet argumentuma.
Bár egy függvényosztály VC-dimenzióját általános esetben nehéz meghatározni, N-dimenziós szeparáló hipersík esetén könnyen megmutatható, hogy a VC-dimenzió értéke h=N+1. Ha azonban nemcsak a mintapontok lineáris szeparálását végezzük, hanem maximális margójú lineáris szeparálást biztosítunk, már a (6.45) összefüggéssel megadott felső korlát érvényes. Ez az összefüggés azt mondja, hogy maximális margójú szeparáló hipersík mellett – ha az r margó értéke elegendően nagy – a VC-dimenzió értéke lehet (N+1)-nél kisebb is. Ennek különösen nemlineáris esetben van jelentősége, ahogy ezt a későbbiekben látni fogjuk. Az a tény, hogy egy felső korlát adható a VC-dimenzióra azt jelenti, hogy a megoldás általánosítóképessége a bemeneti tér dimenziójától függetlenül kontrol alatt tartható a szeparálás tartalékának megfelelő megválasztásával.
A tartalék (6.29) összefüggése szerint a margó fordítottan arányos a súlyvektor normájával.
A (6.33) Lagrange kritérium olyan optimalizálási feladatot fogalmaz meg, ahol a tanítópontok megfelelő osztályozásán túl a súlyvektor normanégyzetének minimumát is biztosítani szeretnénk. A szupport vektor gépeknél az osztályozási hiba minimuma mellett a maximális tartalék, vagyis a minimális VC-dimenzió elérésére törekszünk, összhangban a strukturális kockázat minimalizálási elvvel. A szupport vektor gépekre ezért a statisztikus tanuláselméletnek a 2. fejezetben összefoglalt eredményei alkalmazhatók. Ez lényeges különbség, ha a szupport vektor gépeket az előzőekben bemutatott ún. klasszikus hálókkal, de elsősorban a többrétegű perceptronnal hasonlítjuk össze.
Az MLP hálózatoknál a komplexitás a rejtett réteg méretétől függ. A háló struktúrájának rögzítése a rejtett réteg méretét is meghatározza. A tanítás során ezen már nem változtatunk. Ezzel szemben a szupport vektor gépeknél nem a szabad paraméterek száma határozza meg a komplexitás mértékét, hanem a VC-dimenzió, melynek felső korlátja a maximális margó értékével befolyásolható. A kétféle megközelítés közötti alapvető különbség tehát, hogy míg az MLP-nél csak a tapasztalati hiba, addig a szupport vektor gépeknél mind a tapasztalati hiba, mind az általánosítóképeséget befolyásoló komplexitásmérték, a VC-dimenzió minimalizálása megtörténik.
6.3.2. A lineárisan nem szeparálható feladat lineáris megoldása
Az előzőekben tárgyalt maximális margójú lineáris szeparálásra képes megoldás az alapelvek bemutatására alkalmas. A gyakorlatban azonban ritkán találkozunk olyan feladatokkal, melyek úgy szeparálhatók lineárisan, hogy még osztályozási tartalék is biztosítható. Általában vagy csak olyan lineáris szeparálás lehetséges, ahol a két osztály között csak nagyon kis biztonsági sáv alakítható ki, vagy lineáris szeparálás hibamentesen nem is lehetséges. A kis biztonsági sávot növelhetnénk, ha nem ragaszkodnánk ahhoz, hogy minden tanítópont a sávon kívül helyezkedjen el. Ha a pontok többsége a sávon kívül lesz, de néhány mintapontnál megengedjük, hogy a sávon belülre kerüljenek (sőt esetleg azt is megengedjük, hogy egyes mintapontok az elválasztó hipersík „rossz” oldalára kerüljenek), akkor ezen az áron a sáv mérete esetleg jelentősen növelhető. A következőkben olyan lineáris megoldást mutatunk be, ahol megfelelő kompromisszum alapján dől el a biztonsági sáv mérete és a hibás osztályozás valószínűsége.
Ha megengedjük, hogy a biztonsági sávban is legyenek tanítópontok, miközben továbbra is cél a lehető legnagyobb margó biztosítása, ún. lágy vagy szoft margójú megoldásról beszélünk. Azoknál a pontoknál, amelyek a biztonsági sávon belül helyezkednek el a maximális margójú osztályozást biztosító
(6.46)
egyenlőtlenség nem áll fenn. Az ilyen mintapontokra vonatkozó, az előző egyenlőtlenségnek megfelelő formális kapcsolat ún. gyengítő (slack) ξi változók bevezetésével lehetséges. A gyengítő változók bevezetése lehetővé teszi, hogy a (6.46) összefüggés az egyes tanítópontoknál különböző mértékben gyengítve érvényesüljön. Ennek megfelelően az összes pontra most a következő egyenlőtlenség írható fel:
i=1,2,…,P (6.47)
Azon tanítópontoknál, ahol
, visszakapjuk az alapfeladatot. Ha
, az adott tanítópont a hipersík megfelelő oldalán, de a biztonsági sávban vagy a sávhatáron helyezkedik el, ha pedig
az adott tanítópont a sík ellenkező oldalán (a hibás oldalon) van. Ezt illusztrálja a 6.4 ábra.
Az optimális hipersíkot úgy kell meghatározni, hogy a hibás osztályozások száma minimális legyen, miközben továbbra is törekszünk a lehető legnagyobb margó elérésére. A minimalizálandó kifejezés − amit a továbbiakban J(w)-vel jelölünk − ennek megfelelően két tagból áll:
, (6.48)
ahol C a két tag közötti kompromisszumot beállító együttható. Ha C=0, visszakapjuk az előző, gyengítő változó nélküli esetet. Ha C értéke kicsi, a minimalizálandó összefüggésben a második tag súlya kicsi, vagyis nem nagyon büntetjük, ha egy tanítópont a margón belülre, netán a rossz oldalra kerül. Ez azt jelenti, hogy a biztonsági sáv szélesebb lehet, de több pont kerül a sávon belülre vagy a rossz oldalra. Ha C értékét növeljük, ezeket az eseteket jobban büntetjük, ami keskenyebb biztonsági sávot eredményez, hiszen ekkor nyilván kevesebb pont eshet a sávon belülre.
A megoldás most is a megfelelő Lagrange kritérium felírását igényli, hiszen itt is feltételes szélsőérték-keresési feladattal állunk szemben. Egyfelől (6.48) minimumát kívánjuk elérni, de közben a (6.47) által a tanítópontokra megfogalmazott egyenlőtlenségeket is teljesíteni kívánjuk. Ennek megfelelően a következő Lagrange kritériumot tudjuk felírni.
(6.49)
A kritérium a (6.47) által a tanítópontokra megfogalmazott gyengített feltételek figyelembevételén kívül egy új taggal is bővült. Az utolsó tag – amely szintén egy Lagrange multiplikátoros tag − azt fejezi ki, hogy törekszünk arra, hogy a
értékek lehetőleg nullák, de legalábbis minél kisebbek legyenek. Itt
-k a megfelelő Lagrange multiplikátorok. A módosított Lagrange kritériumot w, b és
-k szerint minimalizálni, míg
-k és
-k szerint maximalizálni kell. A feladatot most is két lépésben oldhatjuk meg. Először a Lagrange kritérium w , b és
szerinti deriváltját írjuk fel.
, (6.50)
(6.51)
. (6.52)
Ezt követően a gradiensek értékének nullává tételével kapott összefüggéseket behelyettesítve a Lagrange kritériumba kapjuk a (6.38) összefüggéssel megegyező duális feladatot:
, (6.53)
ahol
, (6.54)
és melyből az
-k most is kvadratikus programozással határozhatók meg. Figyeljük meg, hogy a gyengítő változók bevezetése az optimalizálási feladat duális alakját csak a Lagrange multiplikátorokra vonatkozó feltételekben módosítja. Az osztályozó eredménye is megegyezik a lineárisan szeparálható feladatra megadottakkal (6.41). Ennek megfelelően itt is lesznek nulla értékű
-k, melyekhez tartozó tanítópontok nem vesznek részt a kimenet előállításában. Ha pedig
, a megfelelő tanítópontok szupport vektorok lesznek, melyekre a
(6.55)
egyenlőség áll fenn. Ez azt jelenti, hogy most a szupport vektorok sem feltétlenül a margó határán helyezkednek el. A margóhoz viszonyított helyzetüket a
értékek befolyásolják.
A (6.48) minimalizálandó kritériumban szereplő
konstanst hiperparaméternek is szokás nevezni. Szerepe – ahogy az előbb említettük – az, hogy a súlyvektor hosszának, illetve a tanító mintákra számított osztályozási hibának a viszonyát beállítsa. C meghatározása nem könnyű feladat, általában kereszt kiértékeléssel történhet.
A szoft margójú lineáris szeparálás általánosító képessége
A gyengítő változó bevezetése azt eredményezte, hogy az összes pont már nem esik a biztonsági sávon kívülre. Ennek a megoldás általánosítóképességére is lesz hatása. A VC-dimenzió (6.45) összefüggése a szoft margójú megoldásra már nem lesz érvényes, így nem lesz érvényes a valódi kockázat felső korlátját megadó (2.31) összefüggés sem. Azonban a lágy margójú megoldás általánosítási hibájára is származtattak felső korlátokat, melyek figyelembe veszik a gyengítő változók értékeit is. Ezek bemutatásával itt nem foglakozunk. A származtatás és az eredmények az irodalomban [Cri00], [Sha02] megtalálhatók.
6.3.3. Nemlineáris szeparálás
A valós osztályozási feladatok túlnyomó része nem szeparálható lineárisan. A lineárisan nem szeparálható feladatoknál – ahogy ezt már többször láttuk – egy megfelelő (és általában dimenziónövelő)
nemlineáris transzformációval lineárisan szeparálhatóvá alakítjuk a feladatot. Az SVM előnyeinek kihasználására az így kapott jellemzőtérben az előzőeknek megfelelő optimális (maximális margójú) megoldást keressük.
A nemlineárisan szeparálható feladat SVM-el történő megoldásában tehát két lépés szerepel:
-
nemlineáris transzformáció a bemeneti térből a jellemzőtérbe,
-
a jellemző térben az optimális lineáris szeparáló hipersík meghatározása.
Ez utóbbi lépést azonban itt sem a jellemzőtérben, hanem az ebből származtatott kernel térben oldjuk meg.
A nemlineáris megoldás a lineáris eset megoldásából egyszerűen az
helyettesítéssel nyerhető. Az optimális hipersíkot a következő alakban keressük:
(6.56)
Ennek alapján a korábbi lineárisan szeparálható esetre kapott eredményünknek megfelelően az optimális súlyvektor:
, (6.57)
ahol
az
mintához tartozó jellemző (feature) vektor. Az optimális eltolásérték (bias) (
) a
vagy a
egyenletből számítható, ahol
egy-egy megfelelő osztályba tartozó szupport vektor. A jellemzőtérben megkonstruált szeparáló felületet tehát a következő egyenlet adja meg:
. (6.58)
Látható, hogy a megoldáshoz most is csak az
Lagrange multiplikátorok meghatározása szükséges, amit a (6.38) összefüggésnek megfelelő duális feladat kvadratikus programozással történő megoldásával nyerhetünk. A különbség mindössze annyi, hogy a duális feladatnál x helyére mindenhol
kell kerüljön. Ha a jellemzőtérben maximális margójú megoldás kapható, akkor a Lagrange multiplikátorokra az
feltétel, ha csak a gyengített változat, akkor az
feltétel teljesül.
A
szorzatot a kernel trükknek megfelelően egy magfüggvényként írjuk fel, azaz
. (6.59)
A nemlineáris osztályozó tehát:
(6.60)
alakban adja meg egy x bemenetre a választ. Az összegzés az összes tanítópontra vonatkozik, valójában azonban csak a szupport vektorokra kell elvégezni, hiszen a többi esetben
. A szupport vektor gépek tehát nemlineáris esetben is ritka (sparse) megoldást eredményeznek.
A szupport vektor gépes megoldás előnye a kerneles megoldások előnyéhez hasonlóan itt is azáltal jelentkezik, hogy a feladatot nem a jellemzőtérben oldjuk meg, hanem a kernel térben, azáltal, hogy a
nemlineáris transzformációt nem közvetlenül, hanem csak a kernel függvényen keresztül, közvetve definiáljuk.
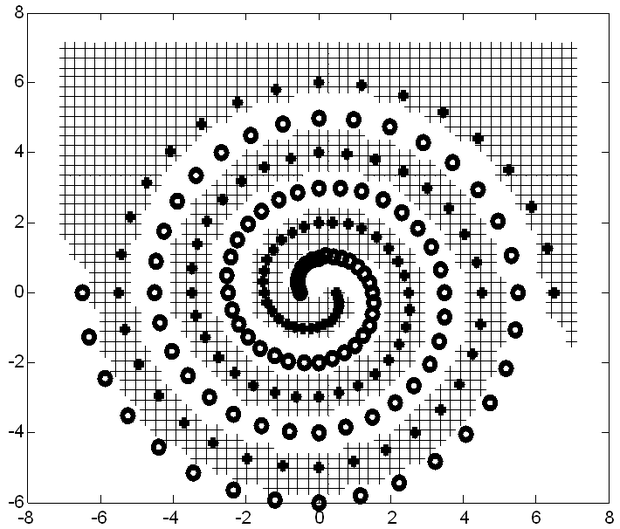
A 6.5 ábrán a nemlineáris SVM osztályozás illusztrálására gyakran használt kettős spirál feladat egy megoldását mutatjuk be. A szeparálandó két osztály két egymásba tekeredő spirál pontjaival van megadva, melyek tanítópontokként szerepelnek. A két osztályba tartozó tanítópontokat (+), illetve (o) jelek jelölik az ábrán. A feladat tehát olyan elválasztó görbe meghatározása, mely a két spirál pontjait szeparálja. A feladatot, mint benchmark problémát gyakran használják osztályozó rendszerek, köztük neuronhálók teljesítőképességének összehasonlítására. Ezt az indokolja, hogy bár a feladat nagyon egyszerűnek tűnik, megoldása nem könnyű, pl. egy MLP számára különösen nehéz.
6.1 példa
Példaként oldjuk meg a XOR problémát szupport vektor géppel. Minthogy a feladat lineárisan nem szeparálható, csak a nemlineáris változat használható. Első lépésként meg kell választani a kernel függvényt. A feladat viszonylagos egyszerűsége miatt az eddig említett kernel függvények bármelyike használható. Jelen esetben használjunk polinomiális kernelt: K(x,x)=(xTx+1)2. A polinomiális kernel előnye, hogy ebben az egyszerű esetben még a jellemzőtérre való leképezést biztosító ϕ(x) függvények is meghatározhatók. A jellemzővektorra a következő adódik:
(6.61)
Látható, hogy a jellemzőtér egy 6-dimenziós tér (5 dimezió + az eltolás). Az osztályozási feladat megoldásához fel kell írnunk és meg kell oldanunk a duális egyenletet.
, (6.62)
a következő feltételek mellett:
(6.63)
A kvadratikus egyenlet felírásánál feltételeztük, hogy a bemenetek és a kimenetek nem bináris, hanem bipoláris megadásúak, vagyis a XOR probléma leképezése a következő:
A kvadratikus programozási feladat megoldásához fel kell írni a kernel mátrixot. Mivel a XOR problémánál összesen 4 pontunk van, melyek mind tanítópontok, a kernel mátrixra a következő adódik:
(6.64)
A kvadratikus programozás eredményeképpen azt kapjuk, hogy mind a négy α azonos értékű lesz, és mind különbözik nullától:
. Ez azt jelenti, hogy az összes pont szupport vektor, ami a feladat ismeretében nem meglepő. A szupport vektoroknál a háló válasza alapján az eltolásérték is meghatározható, ami b*=0-ra adódik. A háló válasza a kernel térben tehát:
(6.65)
A szupport vektor gépeknél a jellemzőtérbeli reprezentáció és megoldás általában nem határozható meg, és nincs is rá szükség. Ebben az egyszerű példában azonban ismerjük a jellemzőtérre való leképezést biztosító
függvényeket, és a Lagrange multiplikátorok ismeretében a w* jellemzőtérbeli súlyvektor is meghatározható:
(6.66)
Ennek ismeretében a megoldás a jellemzőtérben is megkapható. A döntési függvény:
g(x)=x1x2. (6.67)
Arra az érdekes eredményre jutottunk, hogy bár a választott kernel által meghatározott nemlineáris transzformáció hatdimenziós jellemzőteret definiál, a döntés egyetlen dimenzió alapján meghozható, melyet a két bementi komponens szorzata határoz meg. Ez egyben arra is példa, hogy előfordulhat olyan eset, amikor a „dimenziónövelő” nemlineáris transzformáció valójában kisebb dimenziójú térbe képez le, mert a lineáris szeparálás ott is lehetséges. Ez természetesen általánosan nem igaz, de feladattól függően, ha megfelelő nemlineáris transzformációt választunk, előfordulhat. A nemlineáris SVM a jellemzőtérben biztosítja a maximális margót, ami itt
-re adódik.
6.3.4. Szupport vektor gépek regressziós feladatra
A szupport vektor gépekaz osztályozási feladatokon túl regressziós feladatokra is alkalmazhatók. A regressziósvagy függvényapproximációs feladatok esetén azonban nem definiálható az osztályozásnál értelmezett margó, azaz az osztályozási tartalék fogalma. Ennek megfelelően szükség van a regressziós feladat egy olyan értelmezésére, felírására, ami lehetővé teszi az SVM kiegészítő feltételének felhasználását.
Hasonlóan az osztályozónál bemutatottakhoz itt is lehetőség lenne először a lineáris esetet, majd annak nemlineáris kiterjesztését tárgyalni, de a tömörebb tárgyalás kedvéért itt közvetlenül a nemlineáris (azaz a jellemzőtérben lineáris) regressziót mutatjuk be.
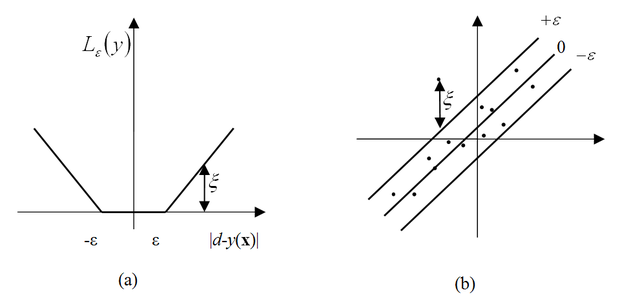
Az osztályozós és a regressziós feladatok között a kapcsolat viszonylag könnyen megteremthető, ha a függvényapproximációs feladatoknál az átlagos négyzetes hiba helyett egy ún. ε-érzéketlenségi sávvalrendelkező abszolútérték hibafüggvényt (ε-insensitive loss function) alkalmazunk az eltérés mérésére.
(6.68)
Az ε érzéketlenségű veszteségfüggvény felhasználásával tulajdonképpen az osztályozási esethez nagyon hasonló probléma áll elő. Azokra a mintákra, melyek az érzéketlenségi sávon belül esnek, a hiba értéke 0, míg a kívül eső pontok hibáját büntetjük. Ez megfeleltethető egy olyan osztályozási feladatnak, ahol a helyes osztályozás hibája 0, míg biztonsági sávba eső vagy a rosszul osztályozott pontokat pedig gyengítő (
) változók bevezetésével büntetjük. Ennek megfelelően az alábbiakban bemutatott regressziós megoldást a lineárisan nem szeparálható osztályozási feladatra kapott eredményekkel célszerű összevetni. Hibafüggvényként az abszolútérték-függvény használatát az is indokolja, hogy ekkor a megoldás az esetlegesen jelen lévő kilógó adatokra (outlier) kevésbé lesz érzékeny, mint a gyakran alkalmazott négyzetes hibafüggvénynél. Ennek ellenére szokás ε-érzéketlenségi sávú négyzetes hibafüggvényt is alkalmazni. Jelen tárgyalásnál azonban megmaradunk a Vapnik féle alapmegoldásnál, ahol az abszolútérték-függvény szerepel.
Írjuk fel a háló kimenetét. Ez most is nemlineáris bázisfüggvények lineáris kombinációjaként áll elő, azaz a
-ek által reprezentált (M-dimenziós) jellemzőtérben lineáris megoldást keresünk:
,
,
(6.69)
A kielégítendő feltételek (a gyengítő változók bevezetésével) a következők:
(6.70)
A minimalizálandó költségfüggvény:
(6.71)
a (6.70) egyenlőtlenségek által megfogalmazott mellékfeltételekkel (
):
A megfelelő Lagrange kritérium az
Lagrange multiplikátorok felhasználásával:
(6.72)
A Lagrange függvényt kell w, b és a
és
gyengítő vektorváltozók szerint minimalizálni,
, valamint
és
szerint maximalizálni. Elvégezve a deriválást, és a deriváltak értékét nullává téve, a következő összefüggéseket kapjuk:
(6.73)
Behelyettesítve ezeket a Lagrange függvénybe jutunk a duális feladatra:
(6.74)
a
(6.75)
megkötésekkel. Az eredmény a kvadratikus programozással meghatározható
Lagrange multiplikátorok, a kiszámított
és a
kernel függvény alapján:
(6.76)
Csakúgy, mint az osztályozási esetben, az SVM modell most is ritka, ugyanis csak azok a tanítópontok vesznek részt a kimenet előállításában, melyekre
. Fontos megjegyezni, hogy most is a kernel függvényből indulunk ki, így a jellemzőtér bázisfüggvényeit a kernel függvény implicit módon definiálja. Ez a jellemzőtér azonban nagyon nagy dimenziós, akár végtelen dimenziós is lehet, ezért míg lineáris esetben a probléma az eredeti térben is megoldható, nemlineáris esetben a jellemzőtérben már nem minden esetben lehetséges a megoldás.
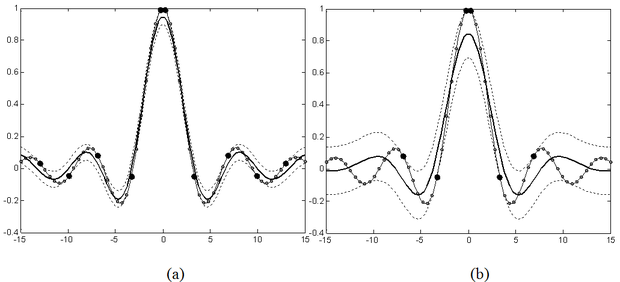
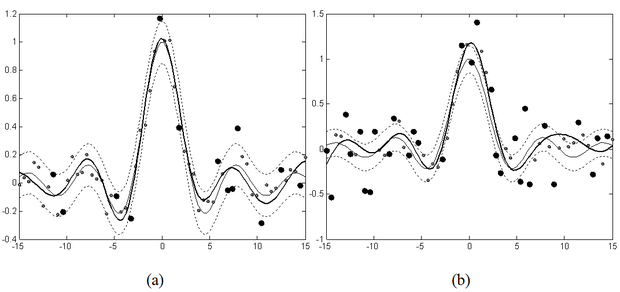
Figyeljük meg, hogy a regressziós megoldásnál az SVM kialakításában az osztályozós esethez képest eggyel bővül a hiperparaméterek száma, hiszen az ε érzéketlenségi paraméter megadására is szükség van. Az ε hiperparaméternek az approximációra gyakorolt hatása zajmentes tanítópontok esetén szemléletesen is értelmezhető (6.7 ábra).
Az ábrán látható, hogy ha a megoldás köré egy ε szélességű sávot húzunk úgy, hogy az SVM válaszfüggvényét
-nal eltoljuk, akkor minden tanítópont ezen a sávon belül helyezkedik el. A sávhatárra eső pontok lesznek a szupport vektorok (az ábrán a nagyobb fekete pontok). Az ábra azt is mutatja, hogy kisebb szélességű sáv több, a nagyobb szélességű pedig kevesebb szupport vektort eredményez. Ezt úgy biztosítja az SVM, hogy minél nagyobb ε értéke, annál simább megoldást kapunk. Ezt a hatást illusztrálja a 6.8 ábra is. Ezen az ábrán is szerepel egy ε szélességű sáv, ami azonban most az approximálandó függvényt veszi közre, és annak
-nal történő eltolásával kapható. Az SVM zajmentes esetben mindig olyan megoldást ad, amely ebbe az ε szélességű sávba belefér, miközben a válasz a lehető legsimább. Látható, hogy a szélesebb sáv simább, a keskenyebb kevésbé sima megoldást eredményez.
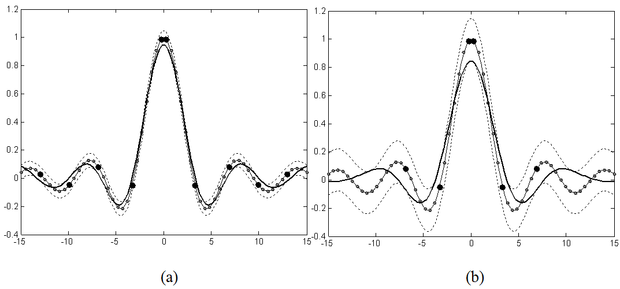
Fentiek alapján ε hatása zajmentes esetben jól követhető, és ennek alapján a megfelelő ε érték megválasztható, hiszen minél kisebb ez az érzéketlenségi sáv, annál pontosabban próbálja a modell a tanítópontokra illeszteni a megoldást. A valós feladatokban azonban szinte mindig zajos bemenetekkel van dolgunk.
Ebben az esetben a kis ε arra késztetné a modellt, hogy minden pontot jól (kis hibával) közelítsen, ami túltanuláshoz vezethet, holott a cél itt éppen egy simább függvény illesztése lenne. Nagyobb zaj esetén tehát célszerű nagyobb ε-t, szélesebb érzéketlenségi sávot használni. Zajos tanítópontok mellett ε hatására a 6.9 ábra mutat példát.
Az SVM minél simább válasza annak a következménye, hogy a súlyvektor normáját minimalizáljuk. A költségfüggvényben szereplő
tag osztályozós esetben a maximális margóért, regressziós esetben pedig a sima és minél laposabb megoldásért felelős.
A megoldás hibája, valamint komplexitása közötti kompromisszumot regressziós esetben is a C paraméter állítja be, azaz az ε és a C hiperparaméterek értékét összehangoltan kell megválasztani. Általánosságban is elmondható, hogy a szupport vektor gépek hiperparamétereinek (az ε, a C, valamint a kernel függvény paramétereinek – Gauss kernel esetén a
szélességparaméternek) a megválasztása igen összetett feladat, mert az egyes paraméterek nem függetlenek egymástól, így a lehetséges beállítások terében kell egy jó, esetleg optimális kombinációt megtalálni. A kernel paraméterek hatása – ha Gauss kernelt választunk – hasonló a Gauss bázisfüggvényes RBF hálók szélességparaméterének hatásához: a nagy
simább, míg a kis
változékonyabb (erősen lokalizált) közelítést eredményez, ami hatással van például a megfelelő C értékre is. C értékét az előbbi esetben kisebb, míg az utóbbi esetben várhatóan nagyobbra kell megválasztani. A hiperparaméterek megfelelő megválasztásával számos irodalom pl. [Sch02], [Cha02], [Kwo03] foglalkozik.
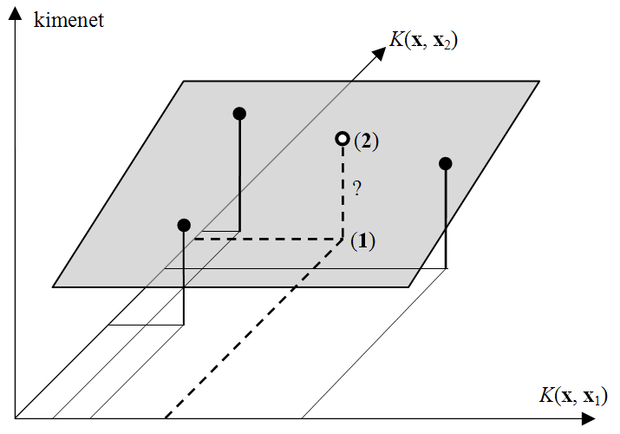
Láttuk, hogy a nemlineáris problémák lineáris kezelésének kulcsa, hogy az eredeti feladatot egy olyan többdimenziós térbe transzformáljuk, ahol az már lineárisan megoldható. A kernel gépek mindezt a kernel térben tudják megoldani. A szupport vektor gépek ezt kiegészítik azzal, hogy a lineáris megoldás kiszámításához olyan módszert adnak, ami alapján a lehetséges megoldások közül a legjobb számítható ki.
A működés mechanizmusának jobb megértéséhez a kernel tér alábbi jellemzőit hangsúlyozzuk:
-
A kernel tér a jellemzőtér, illetve az ehhez tartozó leképezés konkrét ismerete nélkül is elérhető.
-
A kernel tér véges dimenziójú.
-
A kernel függvény és a kernel középpontok (szupport vektorok) ismeretében minden bemeneti vektor leképezhető a kernel térbe.
A probléma a kernel térben már lineáris, így itt az SVM-nek megfelelő optimális hipersíkot kell meghatározni. Ez osztályozás esetén megfelel a kernel térbe leképezett két ponthalmazt (a jellemző térben) maximális margóval elválasztó hipersíknak, regresszió esetén pedig a kernel térbeli pontokra illesztett hipersíknak. A tanítási lépés során tehát a hipersíkot leíró egyenlet szabad paramétereit, az
Lagrange multiplikátorokat és b-t kell meghatározni.
Amennyiben a szupport vektorok száma M, a kernel tér (M+1) dimenziós, ahol M koordinátát a
kernel leképezéssel számítunk ki, míg a további egy dimenzió a kimenetnek felel meg. A keresett hipersík a leképezett tanítópontok és a hozzájuk tartozó kimenet közötti összerendelést definiálja. A működés szemléltetéséhez tekintsük a regressziós esetet. A megtanított SVM működését a 6.10 ábra szemlélteti.
Az SVM modell eredményét leíró
(6.77)
egyenlet alapján a működés a következő. A vizsgált x bemeneti vektort leképezzük a kernel térbe. Ez a szupport vektoroknak megfelelő számú
kernel érték kiszámítását jelenti. Az eredmény a hipersík által definiált pont a leképezéssel kapott pozícióban.
A regressziós feladat megoldása során az SVM által konstruált optimális hipersík − amennyire lehetséges − jó választ ad a tanító pontokra, azaz illeszkedik rájuk. A modell akkor működik megfelelően, ha nemcsak a tanítópontok esetében, hanem később a teszteléshez használt pontok esetén is a hipersíkra esik a kimenet, vagy másképpen a hipersík értéke jól közelíti a valós kimenet értéket.
6.3.5. Az SVM neurális értelmezése
Bár a gyakorlatban a szupport vektor gépeket ritkán alkalmazzák neurális hálózat alakjában, ez az értelmezés hasznos, mert egyszerűbb tárgyalásmódot tesz lehetővé a pusztán matematikai megközelítésnél.
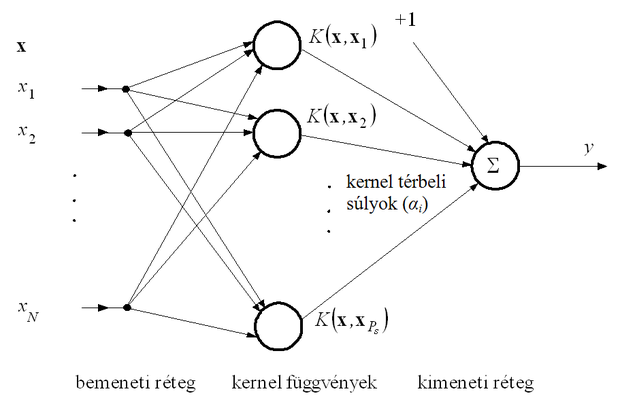
A szupport vektor gépek tanítása, és használata is megfelelő számítások sorozata, ahol a válasz számításának összefüggése pontosan megfeleltethető egy egy-rejtett-rétegű neurális hálózatnak. A rejtett réteg tipikusan nemlineáris neuronokat tartalmaz. A 6.11 ábra egy szupport vektor gépnek megfeleltethető neurális hálózatot mutat be.
A bemenet egy N-dimenziós vektor. A nemlineáris kernel függvényeket a rejtett réteg neuronjai tartalmazzák. Ezen neuronok száma megegyezik a szupport vektorok számával (Ps). A hálózat válasza (
) a rejtett réteg neuronjai kimenetének súlyozott összege. A súlyokat a tanítás során kiszámított Lagrange multiplikátor értékek (
) határozzák meg. Ennek megfelelően, minél kisebb a hálózat, annál kevesebb számításra van szükség a válasz megadásához, így a cél a lehető legkisebb hálózat elérése.
Láthatóan a kernel gép neurális interpretációja egy struktúrájában a bázisfüggvényes hálózatokkal gyakorlatilag tökéletesen megegyező háló. Ez azonban csak formai hasonlóság, a kétféle megközelítés közötti lényeges különbséget nem szabad szem elől téveszteni.
6.3.6. Az SVM hatékonyabb megvalósításai
A szupport vektor gépek gyakorlati felhasználásának egyik legnagyobb akadálya az SVM tanításához szükséges kvadratikus programozás nagy algoritmikus komplexitása, valamint a kernel mátrix nagy mérete. Az alábbiakban olyan módszereket mutatunk be röviden, melyek a számítás gyorsítását, valamint a szükséges memória méretének csökkentését célozzák. Ezt a feladatot kétféleképpen oldhatjuk meg. Ezek:
-
az eredeti felírás megoldásához szükséges számítások (a kvadratikus programozás) felgyorsítása, valamint ezek kisebb tárterületen történő megoldása,
-
az eredeti felírás módosítása úgy, hogy könnyebben megoldható legyen, s így gyorsabb algoritmussal hasonló tulajdonságú megoldásra vezessen. Itt olyan módosításról beszélünk, ami az eredeti SVM optimumot adja, tehát a feladatot nem, csak annak matematikai felírását változtatja. (A későbbiekben olyan SVM változatok bemutatására is sor kerül, ahol azonos elméleti háttér mellet már egy másik probléma (optimum) kerül kiszámításra.)
A QP hatékonyabb megoldása
A tanítási sebesség növeléséhez az SVM tanításban használt kvadratikus programozásilépést kell gyorsabban (és kevesebb memória felhasználásával) végrehajtani. Erre számos hatékony QP megoldó áll rendelkezésre. Ezek iteratív eljárások, amelyek az eredeti optimalizálási feladatot kisebb részfeladatok sorozataként oldják meg. A részfeladatok kiválasztásának alapját az optimalizálási feladat KKT (Karush-Kuhn-Tucker) feltételei jelentik. Azok a minták, amelyek teljesítik az optimumra vonatkozó KKT feltételeket, nem vesznek részt az optimalizálásban, míg a feltételeket megszegő pontok igen. A KKT feltételek osztályozós esetre az alábbiak
-re:
(6.78)
Egy mintapont akkor és csak akkor lehet optimum pontja (6.53)-nak, ha teljesülnek a KKT feltételek és a kernel mátrix pozitív semidefinit.
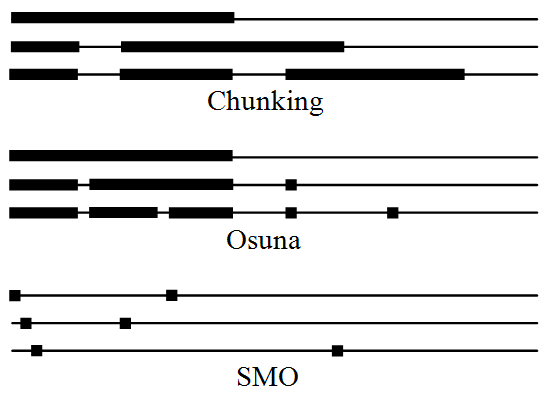
A szupport vektor gépekhez használt három legfontosabb, azonos alapelvek szerint működő, egymást továbbfejlesztő gyorsítási algoritmus [Sch99]:
-
Szeletetés - A szeletelési (chunking) eljárás [Vap79] alapja, hogy a nulla
•
• -khöz tartozó minták nem befolyásolják a megoldást. Először a minták egy részhalmazán oldjuk meg a QP-t, majd az adott alproblémából mindig a szupport vektorokat tartjuk meg. Ezekhez azt az M tanítómintát veszünk hozzá, amelyek a leginkább megszegik a KKT-feltételeket, majd újra megoldjuk a kvadratikus optimalizálást. Ha M-nél kevesebb minta szegi meg a feltételeket, akkor mindet beillesztjük a következő alfeladatba. Az iteráció végére az összes nem nulla multiplikátort meghatározzuk, így az eredeti feladatot is megoldottuk. A kezelt alprobléma nagysága az iterációk során általában nő. A chunking nem jól használható, ha nagyon sok a tanítópont vagy sok a nem nulla
•
• , hiszen ebben az esetben még mindig nagy a memóriaigény.
-
Osuna algoritmusa - Az előzőhöz hasonló módszer Edgar Osuna dekompozíciós módszere [Osu99], amely mindig egy állandó méretű részhalmazon dolgozik, miközben a többi változót rögzített értéken tartja. A kvadratikus programozást így mindig egy rögzített méretű munkahalmazon oldja meg, és kisebb optimalizálási feladatok sorozatán keresztül jut el a teljes megoldásig.
-
SMO -A Sequential Minimal Optimization (SMO) olyan dekompozíciós eljárás [Pla99], amely során iterációnként mindössze két
•
• változó optimalizálása történik meg. Előnye, hogy teljesen kikerüli a QP számítást, mert a két változó analitikusan is optimalizálható. Két változó analitikus optimalizálása után a következő két
•
• kiválasztására kerül sor, amely heurisztikusan történik.
A 6.12 ábra az említett három alapeljárás szeletelési stratégiáját mutatja. Mindhárom módszernél három lépést mutat az ábra, ahol a legfelső a kezdőlépés. A vízszintes vonalak minden esetben a tanító készletet reprezentálják, a megvastagított fekete szakaszok pedig az adott iterációs lépésben optimalizált Lagrange multiplikátorokat jelzik.
Az SVM módosított verziói közül a hatékonyság és a memóriaigény szempontjából Olvi Mangasarian és munkatársainak a munkái a legfontosabbak.
Az SSVM (Smooth Support Vector Machine) [Lee01a] az eredeti feladatot egy olyan optimalizálási feladatra fogalmazza át, ami egyszerű gradiens módszerekkel megoldható. Az így kapott kvadratikus hibafelület minimuma (itt már nincsenek feltételek, mint az eredeti QP-ben) megfelel az SVM által megoldott kvadratikus programozási feladat minimumának.
Az RSVM (Reduced Support Vector Machine) [Lee01b] valójában az SSVM egy kiterjesztése, ahol az összes mintapontnak csak egy részhalmazából kerülhetnek ki szupport vektorok. Az eljárás ezzel valójában tovább redukálja a megoldandó feladat méretét, hiszen az eredeti kvadratikus kernel mátrix helyett egy kisebb mátrixot kell csak előállítani. Ennek a kulcsa, hogy ellentétben a kvadratikus programozással, ami csak kvadratikus mátrixra futtatható, a gradiens módszerekkel már egy ilyen egyenletrendszer is megoldható.