6.5. Kernel CMAC: egy LS-SVM gép véges tartójú kernel függvényekkel

Az eddigiekben láttuk, hogy a bázisfüggvényes hálózatok értelmezhetők kernel gépként is, amennyiben a jellemzőtérből a belső szorzat felhasználásával áttérünk a kernel térre. A kernel interpretáció származhat újfajta megközelítésből (szupport vektor gépek), melynek nincs a klasszikus neuronhálók között ekvivalense, de olyan úton is származtatható, hogy az eredmény valójában a klasszikus bázisfüggvényes megoldással ekvivalens (LS-SVM, ridge regresszió és változataik). Az előbbi esetben a komplexitásra vonatkozó előnyökön túl további előnyök is jellemzik a kernel gépeket: a szupport vektor gépeknél az általánosító-képességre is megfogalmazhatók állítások. Az utóbbi esetben ilyen következménye nincs a kernel megközelítésnek. A komplexitás jelentős redukciója, a limitált komplexitás biztosítása azonban önmagában is jelentős előny. Az LS-SVM vagy a ridge regressziós megközelítést tehát érdemes akkor is alkalmazni, ha ezzel csupán a kapott háló komplexitását tudjuk redukálni. Ennek különösen akkor van jelentősége, ha az eredeti változatot a nagy komplexitás miatt esetleg meg sem tudjuk valósítani, miközben a kernel változat könnyen implementálható. Ilyen esetre ad példát az előző fejezetben bemutatott CMAC háló, amely számos előnyös tulajdonsága ellenére, többdimenziós esetben komplexitás-problémák miatt csak korlátozottan alkalmazható.

A következőkben azt mutatjuk be, hogy ez a komplexitás-probléma a kernel reprezentáció segítségével hogyan oldható meg. A kernel-CMAC származtatásához induljunk ki a CMAC válaszát megadó (5.48) összefüggésből:

y(x)=a(x) Tw. (6.135)

A választ megkapjuk, ha az optimális súlyvektor (5.55) kifejezését ebbe behelyettesítjük. Ezzel egy adott x-re a CMAC válasza:

y(x)=a (x) T w ∗ =a (x) T A T (A A T ) −1 d MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiaabIcacaWH4bGaaeykaiabg2da9iaahggacaqGOaGaaCiEaiaabMcadaahaaWcbeqaaiaadsfaaaGccaWH3bWaaWbaaSqabeaacqGHxiIkaaGccqGH9aqpcaWHHbGaaeikaiaahIhacaqGPaWaaWbaaSqabeaacaWGubaaaOGaaCyqamaaCaaaleqabaGaamivaaaakiaabIcacaWHbbGaaCyqamaaCaaaleqabaGaamivaaaakiaabMcadaahaaWcbeqaaiabgkHiTiaaigdaaaGccaWHKbaaaa@4EA1@ (6.136)

Vegyük észre, hogy ez az összefüggés formailag azonos az egyszerű kernel gép válaszával ((1.9) összefüggés), ha az ottani x ^ MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabCiEayaajaaaaa@36E5@ bemenet helyére a CMAC kimeneti rétegének bemenetét (az asszociációs vektort) helyettesítjük, és hasonlóan az X ^ MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabCiwayaajaaaaa@36C5@ mátrix helyére az asszociációs mátrixot A-t írjuk. A CMAC bázisfüggvényes háló, tehát az asszociációs vektor a bázisfüggvényes hálók φ(x) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacceGae8NXdOMaaeikaiaahIhacaqGPaaaaa@39EF@ vektorának felel meg. Vagyis a CMAC válasza az (6.14) összefüggéshez hasonlóan kernel formában is megadható:

y(x)=a (x) T A T α= ∑ i=1 P α i (a (x) T a( x i ))= ∑ i=1 P α i K i (a(x)) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiaabIcacaWH4bGaaeykaiabg2da9iaahggacaqGOaGaaCiEaiaabMcadaahaaWcbeqaaiaadsfaaaGccaWHbbWaaWbaaSqabeaacaWGubaaaOGaaCySdiabg2da9maaqahabaGaeqySde2aaSbaaSqaaiaadMgaaeqaaOGaaeikaiaahggacaqGOaGaaCiEaiaabMcadaahaaWcbeqaaiaadsfaaaaabaGaamyAaiabg2da9iaaigdaaeaacaWGqbaaniabggHiLdGccaWHHbGaaeikaiaahIhadaWgaaWcbaGaamyAaaqabaGccaqGPaGaaeykaiabg2da9maaqahabaGaeqySde2aaSbaaSqaaiaadMgaaeqaaOGaam4samaaBaaaleaacaWGPbaabeaakiaabIcacaWHHbGaaeikaiaahIhacaqGPaGaaeykaaWcbaGaamyAaiabg2da9iaaigdaaeaacaWGqbaaniabggHiLdaaaa@6548@ . (6.137)

A kernel függvény a CMAC-nál az asszociációs vektorok skalár szorzataként származtatható:

K i (a(x))=a (x) T a( x i )=K(a(x),a( x i ))=K(x, x i ) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4samaaBaaaleaacaWGPbaabeaakiaabIcacaWHHbGaaeikaiaahIhacaqGPaGaaeykaiabg2da9iaahggacaqGOaGaaCiEaiaabMcadaahaaWcbeqaaiaadsfaaaGccaWHHbGaaeikaiaahIhadaWgaaWcbaGaamyAaaqabaGccaqGPaGaeyypa0Jaam4saiaabIcacaWHHbGaaeikaiaahIhacaqGPaGaaeilaiaahggacaqGOaGaaCiEamaaBaaaleaacaWGPbaabeaakiaabMcacaqGPaGaeyypa0Jaam4saiaabIcacaWH4bGaaiilaiaahIhadaWgaaWcbaGaamyAaaqabaGccaqGPaaaaa@58A6@ . (6.138)

Az α MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCySdaaa@3711@ vektor a kernel térbeli súlyvektor:

α= (A A T ) -1 d MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCySdiabg2da9iaabIcacaWHbbGaaCyqamaaCaaaleqabaGaamivaaaakiaabMcadaahaaWcbeqaaiaab2cacaqGXaaaaOGaaCizaaaa@3E9A@ (6.139)

Előfordulhat, hogy az A A T MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCyqaiaahgeadaahaaWcbeqaaiaadsfaaaaaaa@386E@ mátrix nem invertálható, pl. numerikus problémák miatt. Ekkor a szokásos regularizáció alkalmazható, vagyis A A T MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCyqaiaahgeadaahaaWcbeqaaiaadsfaaaaaaa@386E@ helyett a regularizált ( A A T + C −1 I MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCyqaiaahgeadaahaaWcbeqaaiaadsfaaaGccqGHRaWkcaWGdbWaaWbaaSqabeaacqGHsislcaaIXaaaaOGaaCysaaaa@3CD3@ ) mátrixot invertáljuk. Vegyük észre, hogy ekkor valójában egy eltolásérték (bias) nélküli LS-SVM-et oldottunk meg, hiszen – mint láttuk – a mátrix inverziónál bevezettet regularizáció hatása ekvivalens egy olyan LS-SVM megoldásával, ahol a kritériumfüggvénybe a súlyvektor hosszának négyzete, mint minimalizálandó mennyiség is szerepel.

A kernel reprezentáció előnye nyilvánvaló: amíg az eredeti jellemzőtérbeli reprezentációnál a wi súlyok száma a tanítópotok számánál jóval nagyobb (ld. a (5.50)-(5.52) összefüggéseket), addig a kernel térbeli α i súlyok száma a tanítópontok számával egyezik meg. A különbség különösen többdimenziós esetben jelentős. Az 5. fejezetben láttuk, hogy a súlymemória többdimenziós esetben még viszonylag kisméretű (néhány dimenziós) feladatnál is olyan óriási, hogy semmilyen eszközzel nem implementálható. A különféle módosítások (hash kódoló réteg bevezetése, a többdimenziós feladat egy- vagy kétdimenziós részfeladatokra való dekomponálása, stb.) célja az volt, hogy a hatalmas méretű memóriát megvalósítható méretűre redukáljuk. Láthatóan a kernel reprezentáció is egy eszköz az extrém komplexitás letörésére.

A kernel térben a CMAC válaszát kernel függvények súlyozott összegeként állítjuk elő. A kernel gépekre ugyanakkor az is jellemző, hogy a kernel függvényekből indulunk ki, és a jellemzőtérbeli leképezés nemlineáris transzformációját megvalósító φ(x) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacceGae8NXdOMaaeikaiaahIhacaqGPaaaaa@39EF@ leképezést csak implicit módon határozza meg a kernel függvény. A kernel CMAC-nál nem ez a helyzet. Itt valóban a CMAC négyszögletes (bináris) bázisfüggvényeiből belső szorzat útján határozzuk meg a kernel függvényeket.

A bináris véges tartójú bázisfüggvények miatt kernel függvényként egydimenziós esetben a háromszögfüggvényt kapjuk. Többdimenziós esetben a kernel függvény attól függ, hogy teljes lefedést vagy csak C-szeres lefedést alkalmazunk. Az eredeti Albus CMAC esetében az extrém komplexitás miatt a teljes lefedés szóba sem kerülhet, ha a bemeneti dimenzió 3-4-nél nagyobb. A kernel reprezentációnál azonban a komplexitást nem a jellemzőtér, hanem a kernel tér dimenziója határozza meg. A kernel tér dimenziója semmiképpen sem lehet nagyobb, mint a mintapontok száma, bármekkora – akár végtelen – is a jellemzőtér dimenziója. Ez azt jelenti, hogy a kernel reprezentáció esetén nincs szükség a lefedések számának korlátozására, a teljes lefedés is alkalmazható. A kétféle megoldás mindössze annyiban tér el egymástól, hogy más kernel függvényt eredményez, de a kernel függvények száma azonos lesz.

A teljes lefedés azzal az előnnyel is jár, hogy így elkerülhető a C-szeres lefedés következtében előálló approximációs képességbeli korlátozás. Láttuk, hogy többdimenziós esetben a C-szeres lefedésű bináris CMAC csak az additív függvényeket tudja hibátlanul megtanulni (ld. (5.58) konzisztencia-egyenlet). Teljes lefedés, illetve az annak megfelelő kernel változat mellett ez a korlátozás megszűnik.

A 6.20 ábrán a bináris CMAC kernel függvényét mutatja egydimenziós (a) és többdimenziós esetben. A többdimenziós CMAC-nál mind a C-szeres lefedésnek (b), mind a teljes lefedésnek (c) megfelelő kernel függvény látható. A teljes lefedéshez tartozó kernel függvényt kvantált változatban is megadjuk (d).

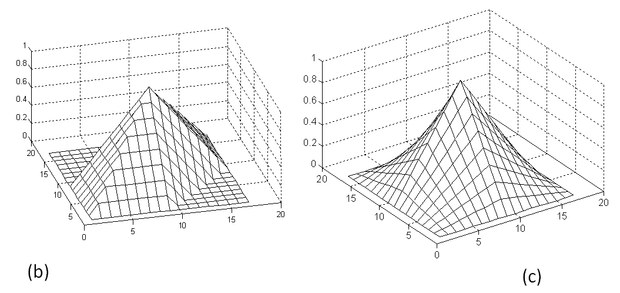
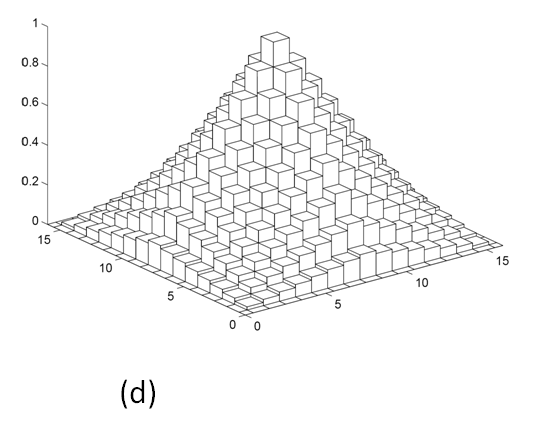
6.20. ábra - A CMAC hálózat kernel függvényei (a) egydimenziós eset, (b) kétdimenziós C-szeres lefedésű, (c) kétdimenziós teljes lefedésű, (d) kétdimenziós teljes lefedésű kvantált.
A CMAC hálózat kernel függvényei (a) egydimenziós eset, (b) kétdimenziós C-szeres lefedésű, (c) kétdimenziós teljes lefedésű, (d) kétdimenziós teljes lefedésű kvantált.

A kernel változatnak azonban van egy hátrányos következménye. Az ábrából látható, hogy a kernel függvények már nem bináris függvények, emiatt a kimenet előállításánál a szorzásokat ténylegesen el kell végezni, a szorzónélküli felépítés, mint előnyös tulajdonság elveszett. A véges tartójú bázisfüggvények következtében azonban a kernel függvények is véges tartójúak, ami azt jelenti, hogy adott bemenet mellett a kimenet előállításában a kernel függvényeknek csak egy töredéke vesz részt, így a szorzások száma is erősen korlátozott.

A válaszokat tekintve a kernel változat ekvivalens az eredeti változattal. Ez azt jelenti, hogy a kernel reprezentáció mellett is megjelenik a nagy általánosítási hiba mindazon esetekben, ha a C/t nem egész (t az egyes dimenziók mentén az egyenletesen elhelyezkedő mintapontok távolságát jelenti kvantumokban mérve). Ennek a hibának a jelentős mérséklését egy súlykiegyenlítő vagy súlysimító regularizáció alkalmazásával értük el (ld. 5. fejezet). A következőkben röviden azt foglaljuk össze, hogy ez a súlykiegyenlítő regularizációa kernel CMAC esetében is alkalmazható.

6.5.1. Kernel CMAC súlykiegyenlítő regularizációval

A regularizált kernel CMAC megoldását a minimalizálandó kritériumfüggvény felírásából származtathatjuk [Hor07].

J( w,e )= 1 2 w T w+ γ 2 ∑ j=1 P e j 2 + λ 2 ∑ j=1 P ∑    i: a j,i =1 ( d j C − w j,i ) 2 MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOsamaabmaabaGaaC4DaiaacYcacaWHLbaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaIXaaabaGaaGOmaaaacaWH3bWaaWbaaSqabeaacaWGubaaaOGaaC4DaiabgUcaRmaalaaabaacciGae83SdCgabaGaaGOmaaaadaaeWbqaaiaadwgadaqhaaWcbaGaamOAaaqaaiaaikdaaaaabaGaamOAaiabg2da9iaaigdaaeaacaWGqbaaniabggHiLdGccqGHRaWkdaWcaaqaaiabeU7aSbqaaiaaikdaaaWaaabCaeaadaaeWbqaamaabmaabaWaaSaaaeaacaWGKbWaaSbaaSqaaiaadQgaaeqaaaGcbaGaam4qaaaacqGHsislcaWG3bWaaSbaaSqaaiaadQgacaGGSaGaamyAaaqabaaakiaawIcacaGLPaaaaSqaaiaayIW7caaMi8UaaGjcVlaadMgacaGG6aGaamyyamaaBaaameaacaWGQbGaaiilaiaadMgaaeqaaSGaeyypa0JaaGymaaqaaaqdcqGHris5aOWaaWbaaSqabeaacaaIYaaaaaqaaiaadQgacqGH9aqpcaaIXaaabaGaamiuaaqdcqGHris5aaaa@6D84@ (6.140)

ahol aj,i a j-edik bemenethez rendelt asszociációs vektor i-edik bitje. (A továbbiakban a négyzetes hibatag együtthatóját γ-val jelöljük az eddigi C-vel szemben, hogy a CMAC C paraméterével való jelölésbeli ütközést elkerüljük.) Látható, hogy a kritériumfüggvény az LS-SVM kritériumfüggvényének felel meg, azzal a különbséggel, hogy egy regularizációs taggal bővült. A regularizációs tag együtthatója λ. Valójában az LS-SVM kritériumfüggvénye is értelmezhető regularizált kritériumfüggvényként, így itt most két egymástól független regularizációt alkalmazunk.

Az LS-SVM-nél szokásos utat követve felírhatjuk a Lagrange függvényt:

L(w,e,α)= 1 2 w T w+ γ 2 ∑ j=1 P e j 2 + λ 2 ∑ j=1 P ∑      i: a j,i =1 ( d j C − w j,i ) 2                     − ∑ j=1 P α j ( w T a j + e j − d j ) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGmbGaaeikaiaahEhacaGGSaGaaCyzaiaacYcacqaHXoqycaqGPaGaeyypa0ZaaSaaaeaacaaIXaaabaGaaGOmaaaacaWH3bWaaWbaaSqabeaacaWGubaaaOGaaC4DaiabgUcaRmaalaaabaacciGae83SdCgabaGaaGOmaaaadaaeWbqaaiaadwgadaqhaaWcbaGaamOAaaqaaiaaikdaaaaabaGaamOAaiabg2da9iaaigdaaeaacaWGqbaaniabggHiLdGccqGHRaWkdaWcaaqaaiabeU7aSbqaaiaaikdaaaWaaabCaeaadaaeWbqaamaabmaabaWaaSaaaeaacaWGKbWaaSbaaSqaaiaadQgaaeqaaaGcbaGaam4qaaaacqGHsislcaWG3bWaaSbaaSqaaiaadQgacaGGSaGaamyAaaqabaaakiaawIcacaGLPaaaaSqaaiaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaamyAaiaacQdacaWGHbWaaSbaaWqaaiaadQgacaGGSaGaamyAaaqabaWccqGH9aqpcaaIXaaabaaaniabggHiLdGcdaahaaWcbeqaaiaaikdaaaaabaGaamOAaiabg2da9iaaigdaaeaacaWGqbaaniabggHiLdaakeaacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiabgkHiTmaaqahabaGae8xSde2aaSbaaSqaaiaadQgaaeqaaOWaaeWaaeaacaWH3bWaaWbaaSqabeaacaWGubaaaOGaaCyyamaaBaaaleaacaWGQbaabeaakiabgUcaRiaadwgadaWgaaWcbaGaamOAaaqabaGccqGHsislcaWGKbWaaSbaaSqaaiaadQgaaeqaaaGccaGLOaGaayzkaaaaleaacaWGQbGaeyypa0JaaGymaaqaaiaadcfaa0GaeyyeIuoaaaaa@9499@ , (6.141)

ami a következő alakra hozható:

L(w,e,α)= 1 2 w T w+ γ 2 ∑ j=1 P e j 2 − ∑ j=1 P α j ( a j T diag( a j )w+ e j − d j )                   + λ 2 ∑ j=1 P d j 2 C −λ ∑ j=1 P d j C a j T diag( a j )w+ λ 2 ∑ j=1 P w T diag( a j )w MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGmbGaaeikaiaahEhacaGGSaGaaCyzaiaacYcacqaHXoqycaqGPaGaeyypa0ZaaSaaaeaacaaIXaaabaGaaGOmaaaacaWH3bWaaWbaaSqabeaacaWGubaaaOGaaC4DaiabgUcaRmaalaaabaacciGae83SdCgabaGaaGOmaaaadaaeWbqaaiaadwgadaqhaaWcbaGaamOAaaqaaiaaikdaaaaabaGaamOAaiabg2da9iaaigdaaeaacaWGqbaaniabggHiLdGccqGHsisldaaeWbqaaiab=f7aHnaaBaaaleaacaWGQbaabeaakmaabmaabaGaaCyyamaaDaaaleaacaWGQbaabaGaamivaaaakiaabsgacaqGPbGaaeyyaiaabEgacaqGOaGaaCyyamaaBaaaleaacaWGQbaabeaakiaabMcacaWH3bGaey4kaSIaamyzamaaBaaaleaacaWGQbaabeaakiabgkHiTiaadsgadaWgaaWcbaGaamOAaaqabaaakiaawIcacaGLPaaaaSqaaiaadQgacqGH9aqpcaaIXaaabaGaamiuaaqdcqGHris5aaGcbaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaey4kaSYaaSaaaeaacqaH7oaBaeaacaaIYaaaamaaqahabaWaaSaaaeaacaWGKbWaa0baaSqaaiaadQgaaeaacaaIYaaaaaGcbaGaam4qaaaaaSqaaiaadQgacqGH9aqpcaaIXaaabaGaamiuaaqdcqGHris5aOGaeyOeI0Iaeq4UdW2aaabCaeaadaWcaaqaaiaadsgadaWgaaWcbaGaamOAaaqabaaakeaacaWGdbaaaaWcbaGaamOAaiabg2da9iaaigdaaeaacaWGqbaaniabggHiLdGccaWHHbWaa0baaSqaaiaadQgaaeaacaWGubaaaOGaaeizaiaabMgacaqGHbGaae4zaiaabIcacaWHHbWaaSbaaSqaaiaadQgaaeqaaOGaaeykaiaahEhacqGHRaWkdaWcaaqaaiabeU7aSbqaaiaaikdaaaWaaabCaeaacaWH3bWaaWbaaSqabeaacaWGubaaaaqaaiaadQgacqGH9aqpcaaIXaaabaGaamiuaaqdcqGHris5aOGaaeizaiaabMgacaqGHbGaae4zaiaabIcacaWHHbWaaSbaaSqaaiaadQgaaeqaaOGaaeykaiaahEhaaaaa@AC1C@ (6.142)

ahol diag(aj) egy olyan diagonálmátrix, melynek főátlójában aj található. A megfelelő deriválások és behelyettesítések elvégzése után itt is egy lineáris egyenletrendszert kapunk, melynek megoldása:

α= ( K D + 1 γ I ) −1 ( I− λ C K D )d MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCySdiabg2da9maabmaabaGaaC4samaaBaaaleaacaWHebaabeaakiabgUcaRmaalaaabaGaaGymaaqaaiabeo7aNbaacaWHjbaacaGLOaGaayzkaaWaaWbaaSqabeaacqGHsislcaaIXaaaaOWaaeWaaeaacaWHjbGaeyOeI0YaaSaaaeaacqaH7oaBaeaacaWGdbaaaiaahUeadaWgaaWcbaGaaCiraaqabaaakiaawIcacaGLPaaacaWHKbaaaa@4A14@ . (6.143)

Itt D= ∑ j=1 P diag( a j ) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCiraiabg2da9maaqahabaGaaeizaiaabMgacaqGHbGaae4zaiaabIcacaWHHbWaaSbaaSqaaiaadQgaaeqaaOGaaeykaaWcbaGaamOAaiabg2da9iaaigdaaeaacaWGqbaaniabggHiLdaaaa@4475@ és

K D =A ( I+λD ) −1 A T MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaC4samaaBaaaleaacaWHebaabeaakiabg2da9iaahgeadaqadaqaaiaahMeacqGHRaWkcqaH7oaBcaWHebaacaGLOaGaayzkaaWaaWbaaSqabeaacqGHsislcaaIXaaaaOGaaCyqamaaCaaaleqabaGaamivaaaaaaa@42E8@ . (6.144)

a regularizált esetnek megfelelő kernel mátrix. Látható, hogy a regularizáció hatására a kernel mátrix megváltozott. A regularizáció tehát módosítja a kernel függvényt. A (6.138) által megadott kernel függvény helyett a

K D,j (a(x))=a (x) T ( I+λD ) −1 a( x j )= K D (a(x),a( x j ))= K D (x, x j ) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4samaaBaaaleaacaWGebGaaiilaiaadQgaaeqaaOGaaeikaiaahggacaqGOaGaaCiEaiaabMcacaqGPaGaeyypa0JaaCyyaiaabIcacaWH4bGaaeykamaaCaaaleqabaGaamivaaaakmaabmaabaGaaCysaiabgUcaRiabeU7aSjaahseaaiaawIcacaGLPaaadaahaaWcbeqaaiabgkHiTiaaigdaaaGccaWHHbGaaeikaiaahIhadaWgaaWcbaGaamOAaaqabaGccaqGPaGaeyypa0Jaam4samaaBaaaleaacaWGebaabeaakiaabIcacaWHHbGaaeikaiaahIhacaqGPaGaaeilaiaahggacaqGOaGaaCiEamaaBaaaleaacaWGQbaabeaakiaabMcacaqGPaGaeyypa0Jaam4samaaBaaaleaacaWGebaabeaakiaabIcacaWH4bGaaiilaiaahIhadaWgaaWcbaGaamOAaaqabaGccaqGPaaaaa@63BE@ . (6.145)

kernel függvényt kapjuk. Mivel D a tanítópontok elhelyezésének függvénye, valójában adatfüggő kernel függvényt kaptunk. A kernel függvény azonban csak a tanítópontoknak a bemeneti térben való elhelyezkedésétől függ, a kívánt válaszoktól nem.

A háló válasza a regularizált esetben a következőre adódik:

y(x)=  a T (x) ( I+λD ) −1 A T [ α+ λ C d ] MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiaabIcacaWH4bGaaeykaiabg2da9iaayIW7caWHHbWaaWbaaSqabeaacaWGubaaaOGaaeikaiaahIhacaqGPaWaaeWaaeaacaWHjbGaey4kaSIaeq4UdWMaaCiraaGaayjkaiaawMcaamaaCaaaleqabaGaeyOeI0IaaGymaaaakiaahgeadaahaaWcbeqaaiaadsfaaaGcdaWadaqaaiaahg7acqGHRaWkdaWcaaqaaiabeU7aSbqaaiaadoeaaaGaaCizaaGaay5waiaaw2faaaaa@5114@ . (6.146)

Ez az alábbi formában is felírható:

y(x)= ∑ j=1 P β j K D (x,  x j ) = K D T (x)β MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiaabIcacaWH4bGaaeykaiabg2da9maaqahabaGaeqOSdi2aaSbaaSqaaiaadQgaaeqaaOGaam4samaaBaaaleaacaWGebaabeaakiaabIcacaWH4bGaaeilaiaabccacaWH4bWaaSbaaSqaaiaadQgaaeqaaOGaaeykaaWcbaGaamOAaiabg2da9iaaigdaaeaacaWGqbaaniabggHiLdGccqGH9aqpcaWHlbWaa0baaSqaamaaCaaameqabaGaaCiraaaaaSqaaiaadsfaaaGccaqGOaGaaCiEaiaabMcacaWHYoaaaa@51EC@ , (6.147)

ahol a β MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCOSdaaa@3712@ együtthatóvektor a módosított kernel függvényekkel felépített kernel térbeli megoldás súlyvektorát jelöli:

β=α+ λ C d MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaCOSdiabg2da9iaahg7acqGHRaWkdaWcaaqaaiabeU7aSbqaaiaadoeaaaGaaCizaaaa@3DB0@ . (6.148)

A regularizálás a kernel reprezentációs megoldás mellett is biztosítja a háló sima válaszát, tehát az általánosítóképesség jelentős javítását. A regularizált kernel CMAC tehát nemcsak a komplexitás jelentős redukcióját biztosítja, hanem az approximációs- és általánosítóképességet is javítja.

A regularizált kernel CMAC azon túl, hogy egy jobb tulajdonságú tanuló rendszert eredményez, arra is példa, hogy regularizációs formában az alapkritérium mellett további mellékfeltételek is belefogalmazhatók egy feladatba. Az eljárás hatékonysága attól függ, hogy az így definiált optimalizálási feladat milyen nehézségek árán oldható meg.