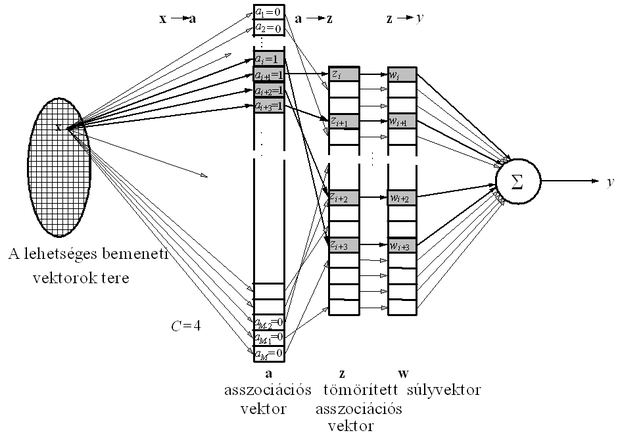
5.2. A CMAC hálózat
A CMAC ( Cerebellar Model Articulation Controller ) hálózatot 1975-ben javasolta James Albus [Alb75]. A perceptronból származtatott hálózat kétlépéses leképezést valósít meg, így sok szempontból rokonítható az RBF hálózatokhoz. A hálózat itt is a bemenet valamilyen nemlineáris transzformációját valósítja meg, majd a transzformált értékek egy lineáris, ellenőrzött tanítású réteg bemenetére kerülnek.
Az RBF és a CMAC hálózatok között az alapvető különbség a nemlineáris leképezésben van. A CMAC hálózat a bemenetet egy ún. asszociációs vektorra képezi le, mégpedig úgy, hogy véges számú, diszkrét bemeneti értéket tételez fel, és minden lehetséges bemeneti értékhez egy kölcsönösen egyértelmű asszociációs vektort rendel. Ez azt jelenti, hogy a CMAC hálózat kvantált bemenetekkel dolgozik. b -bites kvantálót feltételezve, egydimenziós bemenetnél , N -dimenziós bemenetnél különböző bemeneti értékünk lehet. Az egyszerűség kedvéért először az egydimenziós bemenet esetét vizsgáljuk, majd ezután végezzük el a többdimenziós bemenetre való kiterjesztést.
Az egyes bemeneti értékekhez rendelt asszociációs vektor egy olyan sokbites bináris vektor, amelyben minden diszkrét bemeneti értékhez rögzített számú, egymás mellett elhelyezkedő bit lesz aktív (1 értékű), míg a vektor összes többi bitje 0 értéket vesz fel. Az aktív bitek száma − amelyet a továbbiakban C -vel jelölünk − a hálózat fontos paramétere, befolyásolja a hálózat általánosító-képességét. Megjegyezzük, hogy a bináris asszociációs vektor miatt az Albus által javasolt CMAC hálózatot szokás bináris CMAC-nak is nevezni. Később javasoltak ún. magasabbrendű CMAC változatokat is, melyeknél az asszociációs vektor elemei nemcsak bináris értékeket vehetnek fel. Ezekkel a változatokkal a későbbiekben foglalkozunk.
Az asszociációs vektort úgy is elképzelhetjük, mint egy sokelemű neuronréteget, melynek neuronjai közül minden különböző diszkrét bemenetre pontosan C kerül gerjesztett állapotba, vagyis ad 1 értékű kimenetet. A gerjesztett neuronok célszerűen a rétegben egymás melletti helyeken találhatók és olyan módon kerülnek kiválasztásra, hogy az egymáshoz közeli bemeneti értékekre válaszul részben azonos neuronok aktivizálódjanak. Az egyes neuronoknak itt is van érzékelési mezőjük ( receptive field ). Adott bemenetnél mindazon neuronok aktivizálódnak, melyek érzékelési mezői tartalmazzák az adott bemenetet. Minél közelebbi értékek kerülnek a hálózatra, annál nagyobb lesz az átfedés az aktív neuronok, vagyis az asszociációs vektor aktív bitjei között, hiszen a közeli bemenetek nagyrészt azonos érzékelési mezőkbe esnek. Szomszédos, tehát egymástól egy kvantumnyira lévő bemenetekhez a C aktív bitből C -1 lesz közös, míg a legalább C kvantum távolságban lévő bemenetekre adott asszociációs vektor válaszokban már nem találunk közös aktív biteket.
Az érzékelési mezőkkel történő értelmezés alapján az egyes neuronokat tekinthetjük úgy is, mintha minden neuronhoz egy bázisfüggvény tartozna. Ebben az értelmezésben a CMAC háló is egy bázisfüggvényes háló , ahol bináris és valóban véges tartójú bázisfüggvényekkel dolgozunk. Egydimenziós bemenet esetén a bázisfüggvények tartója C kvantumnyi intervallum, míg többdimenziós bemenetnél a tartó egy C kvatumnyi oldalhosszúsággal rendelkező N -dimenziós hiperkocka.
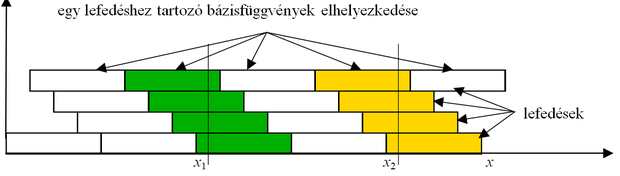
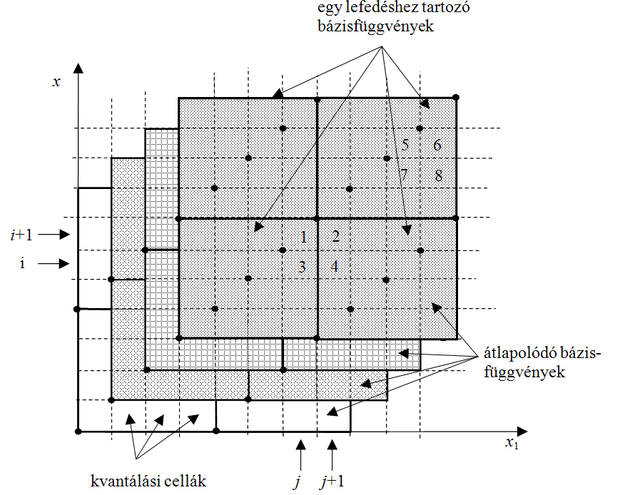
A bázisfüggvényeknek úgy kell elhelyezkedniük, hogy bármely megengedett diszkrét bemenet C bázisfüggvény tartójába essen. Így bármely bemenet hatására C rejtett neuron aktivizálódik. Ezt úgy valósíthatjuk meg, ha minden bemeneti kvantum (elemi cella) a bázisfüggvényekkel C -szeresen lesz lefedve. Egy lefedés azt jelenti, hogy a bázisfüggvények tartói „hézagmentesen” és átlapolódásmentesen a teljes bemeneti tartományt lefedik. Ezt mutatja egydimenziós esetre C =4 mellett az 5.6 ábra.
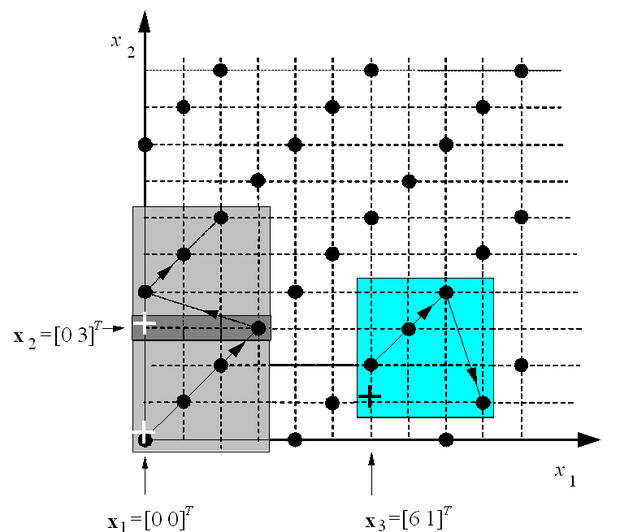
Az ábrán látható, hogy az egyes lefedésekhez tartozó bázisfüggvények tartói egy kvantumnyi távolsággal vannak eltolva egymáshoz képest. Így biztosított, hogy bármely diszkrét bemenet mindig C bázisfüggvény tartójába esik és a szomszédos bemenetek által aktivált bázisfüggvények közül C -1 közös. Az ábrán az is látható, hogy adott bemenetekhez mely bázisfüggvények lesznek kiválasztva: x 1 a sötétebben, x 2 pedig a világosabban árnyékolt bázisfüggvények érzékelési mezőibe esik bele.
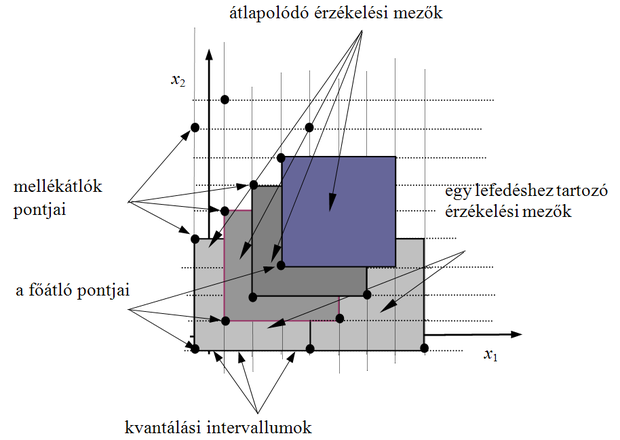
Ha többdimenziós esetben is hasonlóan fednénk le bázisfüggvényekkel a bemeneti teret, akkor a minden dimenzió mentén egy kvantumnyi eltolás azt eredményezné, hogy N -dimenziós esetben C N lefedést lehetne kialakítani. Ezt a lefedést teljes lefedésnek ( full overlay ) nevezzük, és ez azt jelentené, hogy a bázisfüggvények száma a dimenzióval exponenciálisan növekedne (a dimenzió átka probléma). Ha megelégszünk azzal, hogy dimenziótól függetlenül bármely bemenethez C aktív bit tartozzon az asszociációs vektorban, vagyis egy bemenet mindig csak C bázisfüggvény tartójába essen, jóval kevesebb bázisfüggvényre van szükségünk. Az 5.7 ábra kétdimenziós bemeneti tartományra mutatja a bázisfüggvények elhelyezésének egy lehetséges módját, amely a C -szeres lefedést biztosítja C =4 mellett.
Látható, hogy egy lefedés a bemeneti tér teljes „kicsempézését” jelenti. A bázisfüggvények úgy helyezkednek el, hogy minden lehetséges diszkrét bemenet egy lefedésen belül egy és csakis egy bázisfüggvény érzékelési mezőjébe esik. Az asszociációs vektorban a C aktív bit úgy biztosítható, ha pontosan C lefedést alkalmazunk.
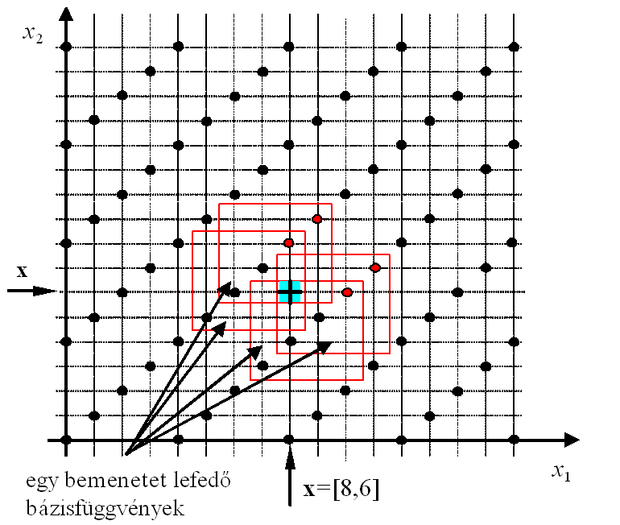
Az 5.8 ábrán egy bemeneti mintapontot (a + jellel megjelölt x pont ) és a kvantált bemenet miatt a pontot is magába foglaló elemi cellát (árnyékolt terület) lefedő C érzékelési mező elhelyezkedése látható ( C =4). Minden egyes érzékelési mező egy bázisfüggvényhez tartozik és minden bázisfüggvény egy bitet jelent az asszociációs vektorban. Az adott x bemenet mellett az ábrán bejelölt érzékelési mezőknek megfelelő asszociációs bitek lesznek aktívak.
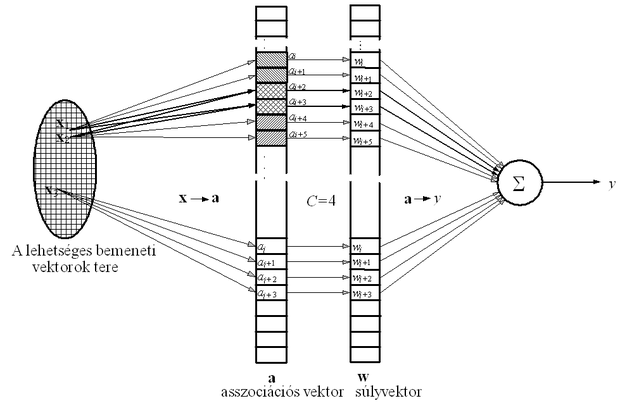
Az asszociációs vektor a hálózat kimeneti rétegének bemenetéül szolgál. Minthogy bináris vektorral van dolgunk, ez azt jelenti, hogy az asszociációs vektorban lévő aktív bitek C súlyértéket választanak ki a kimeneti réteg súlyai közül, majd a kimeneti összegző ezen súlyok összegeként állítja elő a hálózat bemenetre adott válaszát. Vegyük észre, hogy ha C =1, akkor minden diszkrét bemenethez csak 1 aktív bit tartozik az asszociációs vektorban, és a hálózat kimenete ezen bit által kiválasztott súly értéke lesz. Ha tehát az asszociációs vektor pontosan annyi bites, ahány különböző diszkrét bemeneti értékünk lehet, akkor egy egyszerű táblázattal állunk szemben. Ha a táblázat értékei − az egyes súlyok − a diszkrét bemenetekre adandó kívánt válaszok, akkor a hálózat minden diszkrét bemeneti értékre nyilvánvalóan a pontos kívánt választ fogja adni.
A CMAC hálózat alapvető architektúráját és leképezéseit mutatja az 5.9 ábra. A gyakorlatban C értékét egynél nagyobbra, de az asszociációs vektor hosszánál jóval kisebbre választjuk. A bemenetről az asszociációs vektorra való leképezés tulajdonképpen egy bináris kód hozzárendelése a bemenethez, és mivel az M-bites vektorban csupán C<<M aktív bit lesz, a bináris kód ritka kód lesz.
Az aktív bitek határozzák meg, hogy a kimeneti lineáris összegző rétegben mely súlyok összegeként áll elő a kimeneti érték. Az aktív asszociációs bitek elrendezése biztosítja a hálózat általánosító képességet. Két bemeneti vektor, x 1 és x 2 hasonlóságát a hozzájuk tartozó a 1 és a 2 asszociációs vektorok metszete mutatja. Ezt az esetet illusztrálja az 5.9 ábra, ahol a 1 és a 2 aktív bitjei közül kettő közös. Ugyanakkor az ábrán az is látható, hogy egymástól távol lévő bemeneti vektorok ( x 3 és x 1 vagy x 2 ) esetében nincsenek közös aktív asszociációs bitek ( a 3 és a 1 vagy a 2 ). A jobb áttekinthetőség kedvéért az ábrán csak az aktív biteket és az általuk kiválasztott súlyokat jelöltük. Természetesen nem szükséges − és többdimenziós bemenet esetén nem is lehetséges −, hogy minden bemeneti értékhez az asszociációs vektor szomszédos C bitje legyen aktív. A bemenetről az asszociációs vektorokra való leképezésnél mindössze azt kell biztosítani, hogy minél közelebb van egymáshoz két bemeneti vektor, annál nagyobb átfedés legyen az asszociációs vektorok között, vagyis az asszociációs vektorok Hamming távolsága annál kisebb legyen.
A kimeneti érték – hasonlóan bármely más bázisfüggvényes hálózathoz – az asszociációs vektor (a bázisfüggvényes rejtett réteg válasza, a(x ) és a súlyvektor skalár szorzataként határozható meg:
y ( x )= a ( x ) T w. ( 5 . 48 )
A CMAC asszociációs vektora bináris vektor, ezért a skalár szorzást valójában nem is kell elvégezni, elegendő az aktív bitek indexeit ismerni, mivel ezek fogják kijelölni a súlyokat tároló memória azon rekeszeit, amelyekben az adott bemenethez tartozó kimenetet meghatározó súlyok találhatók. A kimenet számítása ezért ténylegesen csak összeadást igényel, ami egyértelmű implementációs előnyt jelent minden eddigi hálóval szemben:
( 5 . 49 )
Az 5.9 ábrán bemutatott elvi felépítésből látható, hogy bár a CMAC hálószintén bázisfüggvényes háló, jelentős mértékben különbözik az előbbiekben tárgyalt RBF hálóktól. A különbségnek több oka van. Egyrészt a CMAC háló kvantált bemenetekkel dolgozik, ezért itt csak véges számú különböző bemenet fordulhat elő. Másrészt az alkalmazott bázisfüggvények nem rendelkeznek szabad paraméterekkel. A háló első rétegének egyetlen megválasztható paraméterét, C-t előre rögzíteni kell, és ebből a háló teljes felépítése következik. Mivel a bázisfüggvények rögzített elhelyezésűek, a CMAC hálóknál valóban csak a kimeneti lineáris réteg súlyait kell meghatározni, ami mind analitikus összefüggés alapján, mind iteratív tanulással (pl. LMS algoritmussal ) lehetséges.
A háló komplexitását is C értéke és a bemenet dimenziója határozza meg. A háló első rétege a kvantált bemenetekből állítja elő az asszociációs vektor aktív bitjeinek megfelelő memóriacímeket. Ezek a címek adják meg, hogy az aktív bitekhez tartozó bázisfüggvények súlyai egy súlymemóriában hol találhatók. Mind az első réteg, mind a második, lineáris réteg komplexitását a bázisfüggvények száma, az asszociációs vektor hossza határozza meg. Az első réteg a diszkrét bemenetek és az asszociációs vektorok között kölcsönösen egyértelmű leképezést valósít meg, tehát minden lehetséges diszkrét bemenethez egy egyedi asszociációs vektor tartozik. Ebből adódik, hogy C aktív bit mellett egydimenziós esetben az asszociációs vektor hossza
( 5 . 50 )
lesz, ahol R a lehetséges diszkrét bemenetek száma. N -dimenziós esetben, teljes ( C N -szeres) lefedésnél ez
( 5 . 51 )
lenne, ami nagyon nagy érték is lehet. Az összefüggésekből látható, hogy az asszociációs vektor közelítőleg annyi bites, mint ahány lehetséges diszkrét bemeneti érték van. Pl. egy 10-dimenziós feladatnál, ahol minden bemeneti komponenst 10 bitre kvantálunk, a lehetséges diszkrét bemeneti vektorok és így az asszociációs bitek száma már megvalósíthatatlanul nagy: . Eddigi formájában a CMAC hálózat súlyait tároló memória tehát csak meglehetősen kis bemeneti dimenzió és durva kvantálás mellett lenne realizálható méretű. Ha a teljes lefedés helyett az előbbiekben már említett C -szeres lefedést alkalmazzuk, akkor az asszociációs vektor hossza közelítőleg már „csak”
( 5 . 52 )
lesz (itt benne lévő értéknél nagyobb legkisebb egészt jelöli). Bár nagyságrendekkel kisebb is lehet, mint M , ha a dimenziószám, N nagy, a címtartomány még mindig akkora, hogy a súlyok tárolásához szükséges memória még mindig irreálisan nagy. Pl. az előzőekben említett 10-dimenziós bemeneti vektorok esetében, ha a bemeneti komponenseket 10 bitre kvantáljuk és C =128, a címtartomány mérete, közelítőleg még mindig 2 37 , ami 128 Gbyte.
A realizálhatóság érdekében a súlyok számát valamilyen módon tovább kell csökkenteni. Ez viszonylag egyszerűen akkor tehető meg, ha van valamilyen a priori ismeretünk a bemeneti mintapontok eloszlásáról. Ha a bemeneti mintatérben vannak sűrűsödési helyek, ahol nagy számban találhatók tanítópontok, akkor elsősorban ezen tartományokhoz kell aktív asszociációs biteket és így súlyokat rendelnünk. A bemeneti mintatér többi részéhez, ahol kis valószínűséggel találunk tanítópontot, egyáltalán ne rendeljünk súlyokat. A priori ismeret hiányában ez a megoldás azonban nem alkalmazható. Iktassunk be ezért egy újabb, tömörítő leképezést az asszociációs vektor és a súlyvektor közé. S minthogy a bemeneti mintapontok eloszlásáról nincs a priori ismeretünk, a legjobb amit tehetünk egy véletlen(szerű) leképezés alkalmazása.
Rendeljünk az a asszociációs vektorhoz egy z ún. tömörített asszociációs vektort úgy, hogy a minden egyes bitjéhez rendeljük hozzá z egy bitjét. A véletlen hozzárendelés miatt az egy bemeneti mintapontra válaszként kapott a asszociációs vektor aktív bitjei között fennálló kapcsolat (pl. szomszédosság) z aktív bitjeire már nem lesz igaz. A súlyokat ezek után nem a, hanem z bitjei választják ki, tehát a kimeneti érték előállításához azon súlyok összegét kell képezni, amelyekre z aktív bitjei mutatnak. A tömörítést is alkalmazó CMAC hálózat leképezéseit az 5.10 ábra mutatja.
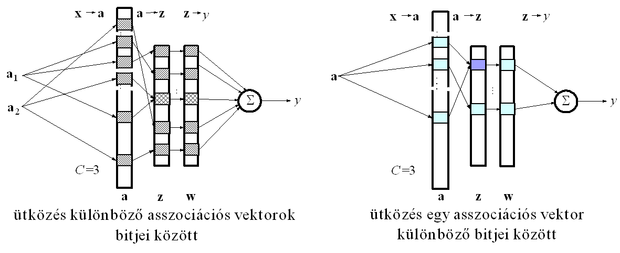
Ha z bitjeinek száma sokkal kisebb, mint a -é, akkor jelentősen csökkenteni tudjuk a súlyok számát. Természetesen e tömörítő leképezés csak úgy valósítható meg, ha megengedjük, hogy a különböző cellái véletlenszerűen ugyanarra a z cellára legyenek leképezve, tehát valójában több-egyértelmű leképezést alkalmazunk. Az eljárás a nem kölcsönösen egyértelmű leképezés ellenére a gyakorlati feladatok megoldásánál jól működik. Ugyanis a hálózat bemenetére a lehetséges diszkrét bemeneti mintáknak rendszerint csak egy kis töredéke kerül, így annak valószínűsége, hogy különböző bemeneti mintákhoz azonos z asszociációs vektorok tartozzanak csaknem nulla. Annak valószínűsége azonban, hogy egymástól távol lévő bemeneti minták z asszociációs vektoraiban közös aktív bitek is legyenek már nagyobb. Ilyen esettel elsősorban akkor találkozhatunk, ha a tömörítés mértéke igen nagy, vagyis z sokkal kisebb méretű, mint a . Ezt a jelenséget "ütközés"-nek hívjuk. Az ütközés következtében az egymástól távol lévő tanító pontok részben azonos súlyokat választanak ki, ami a tanításnál interferenciát okoz. Ha az ütközések valószínűsége kicsi, a hatás elhanyagolható, illetve a tanító lépések számának növelésével az ütközésből adódó interferencia csökkenthető.
Az ütközésnek egy másik fajtája is előfordulhat a tömörítés következtében. Egy bemeneti vektorhoz C aktív bit tartozik az asszociációs vektorban, így előfordulhat, hogy a C bit közül kettőt vagy többet ugyanarra a z -beli bitre képezünk le, vagyis a tömörített vektorban az aktív bitek száma C .
A kétfajta ütközést illusztrálja az 5.11 ábra. Az ütközések gyakorisága a tömörítő leképezés megvalósításától, továbbá az aktív bitek számának a tömörített asszociációs vektor hosszához viszonyított arányától is függ.
Megmutatható, hogy ha az aktív bitek száma kisebb, mint kb. 1%-a a tömörített asszociációs vektor hosszának, akkor csak kis valószínűséggel következik be ütközés. Annak valószínűsége pedig, hogy két eltérő asszociációs vektorban több mint két bitnél is ütközés következzen be, illetve, hogy egy asszociációs vektor kettőnél több bitje ugyanarra a tömörített vektor-bitre legyen leképezve gyakorlatilag nulla. Ez arra utal, hogy megfelelő tömörítő leképezés alkalmazása nem rontja jelentősen a hálózat képességeit [Ell91].
A tömörítő leképezés azt jelenti, hogy a kiinduló (virtuális) címtartományt egy kisebb (fizikai) címtartományra képezzük le. A két címtartomány közötti leképezés hash kódolás saltörténhet. A hashelés (a szó azt jelenti, hogy összekeverni, összezagyválni valamit) véletlenszerű leképezése különösen a tömörítés miatt fontos, hiszen ez biztosítja, hogy az a asszociációs vektor bitjei a kisebb, tömörített asszociációs vektoron belül egyenletesen szétszórva helyezkedjenek el, csökkentve a véletlen ütközés valószínűségét.
A hash kódolás gyakorlati megvalósítására többféle eljárás alkalmazható [Knu88]. A CMAC hálózatoknál jól használható pl. a polinomosztás. Ha a virtuális címtartomány minden egyes címét, mint egy bináris polinomot képzeljük el, akkor ezen polinom osztása során keletkezett maradék-polinom a tömörített, fizikai címtartomány megfelelő címét reprezentálja. Az osztó polinom természetesen befolyásolja a leképezés tulajdonságait, ezért tetszőlegesen nem választható meg. Ennek részleteire azonban itt nem térhetünk ki, csupán a megfelelő irodalomra, pl. [Pet72] utalunk.
A módszert az alábbi példa illusztrálja.
5 .1 Példa
Tételezzük fel, hogy egy 32 megaszó méretű virtuális memóriáról kell a hash kódolás során 64 kiloszavas fizikai memóriára elvégezni a tömörítést. A virtuális memória megcímzéséhez 25 bit szükséges, a fizikai címek megadásához 16 bit elegendő. A polinomosztással történő hashelés tehát azt jelenti, hogy egy 25 bites bináris címet reprezentáló 24-ed fokú polinomot kell elosztanunk egy olyan polinommal, hogy a maradék 16 bites legyen. A virtuális címnek megfelelő polinomot V ( x )-szel, a fizikai címnek megfelelő polinomot P ( x )-szel és az osztó polinomot G ( x )-szel jelölve:
.
A 16 bites fizikai címet 15-ödfokú polinommal reprezentálhatjuk, vagyis G ( x ) fokszáma 16 kell legyen. Legyen az osztó polinom a következő:
Ezzel pl. a 28.792.695 virtuális cím, amelynek 24-ed fokú polinom reprezentációja:
G ( x )-szel történő osztása után a maradékpolinom:
,
vagyis a fizikai cím: 28.401.
Az eddigiekből látható, hogy a CMAC hálózat az egyéb előrecsatolthálózatokkal szemben számos előnyös, és mint látni fogjuk számos hátrányos tulajdonsággal is rendelkezik. Ebben az alfejezetben ezeket a tulajdonságokat elemezzük. Előbb megvizsgáljuk a háló approximációs- és általánosító-képességét, majd a háló tanításával kapcsolatos kérdésekkel foglalkozunk.
A modellező képesség, a hálózat által megvalósítható leképezés tulajdonságainak tárgyalásánál alapvetően két kérdésre keresünk választ: (*) milyen feltételek mellett tudja a CMAC háló pontosan megtanulni a tanító pontokat, továbbá, (**) milyen leképezést valósít meg a háló a tanító pontok között, milyen a háló általánosító-képessége.
Fenti kérdésekre adható válaszok bizonyos mértékig eltérnek az eddig tárgyalt (MLP, RBF) hálózatoknál kapott válaszoktól. Az eltérés a CMAC néhány lényeges specialitásából adódik. Az approximációs képesség szempontjából a CMAC hálózat legfontosabb sajátossága, hogy kvantált bemenetekkel dolgozik, vagyis adott kvantumon belül tetszőleges bemeneti érték mellett a hálózat kimenete azonos lesz. A hálózat ebből adódóan szakaszosan konstans kimenetet szolgáltat, vagyis a megvalósított leképezés eleve nem folytonos. A bemeneti kvantálás felbontását elvben tetszőlegesen finomra is választhatjuk, de ennek gyakorlati korlátai vannak. Egyrészt a bemeneti analóg jel kvantálására szolgáló A/D átalakítók felbontása véges, másrészt minél nagyobb felbontást alkalmazunk, annál nagyobb a hálózat súlyainak száma (ld. az (5.50), ill. az (5.52) összefüggéseket), ami különösen többdimenziós bemenetnél realizálhatatlanná teszi a hálózatot. Itt jegyezzük meg, hogy a bemenet kvantálása nem szükségképpen kell, hogy egyenletes legyen, így azon tartományok, elemi cellák nagysága, amelyeken belül a háló leképezése konstans, a bemenő jeltől függően változhat is [Eld97]. Ugyancsak lehetséges, hogy a kvantálás finomsága dimenziónként eltérő legyen (ld. pl. [Gon98]), vagy több, különböző felbontással dolgozó CMAC háló kombinálásával egy moduláris háló architektúrát alakítunk ki [Moo89].
A továbbiakban a szakaszonként konstans leképezést, mint tényt elfogadva azt vizsgáljuk, hogy a lehetséges kvantált diszkrét bemeneti értékekhez milyen kívánt válaszok előállítására alkalmas a hálózat, vagyis létezik-e olyan súlykészlet, amellyel a tanítópontokban előírt, tetszőleges bemeneti-kimeneti kapcsolatot pontosan előállítja a háló. A tanítópontokban adott válaszok mellett fontos kérdés, hogy a tanítópontok közötti pontokban milyen a háló válasza. Az előbbi kérdést, vagyis a háló tanítópontokban adott válaszainak a minősítését a háló approximációs képességének nevezhetjük, míg az utóbbit az általánosító-képességének. Triviális, de megjegyezzük, hogy általánosító-képességgel csak akkor rendelkezik a háló, ha C> 1.
A háló approximációsképességének vizsgálatánál meg kell különböztetnünk az egydimenziós és a többdimenziós esetet. Egydimenziós esetben tömörítő leképezésre nincs szükség, hiszen itt nincs komplexitásprobléma, ezért a háló leképezését döntően a bemenetről az asszociációs vektorra történő leképezés határozza meg. A háló kimenetét megadó (5.48) összefüggés alapján az összes tanítópontra adott válasz
( 5 . 53 )
formában adható meg. Az A asszociációs mátrix a tanítópontokhoz tartozó asszociációs vektorokból, mint sorvektorokból álló P × M -es mátrix, ahol P a tanítópontok száma, M pedig az asszociációs vektor hossza, amit egydimenziós esetben az (5.50) összefüggés ad meg. Amennyiben a d vektorral megadott kívánt válaszokat szeretnénk megtanítani, a megoldás súlyvektort az
( 5 . 54 )
egyenletet kielégítő (vagy azt átlagos négyzetes értelemben közelítő) w * adja meg. Az asszociációs mátrix semmiképpen nem lehet négyzetes, mivel M > P még akkor is, ha a bemeneti tér minden lehetséges pontja egyben tanítópont is. Az (5.54) összefüggés tehát egy alulhatározott lineáris egyenletrendszer, melynek végtelen sok különböző megoldása lehet. Tetszőlegesen rögzítve (pl. 0-ra választva) M - P súly értékét, ha A rangja P , a lineáris egyenletrendszer egyértelmű megoldásra vezet, amit a pszeudo-inverz segítségével határozhatunk meg.
( 5 . 55 )
Ez a megoldás azt biztosítja, hogy a tanítópontokban a háló válaszai pontosan megegyeznek a kívánt válaszokkal. A háló összes lehetséges bemenetre adott válasza ennek megfelelően az
( 5 . 56 )
formában adható meg, ahol T az összes lehetséges bemenethez tartozó asszociációs vektorokból képezett R × M -es mátrix.
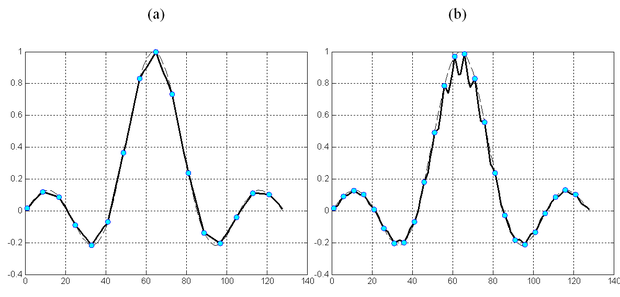
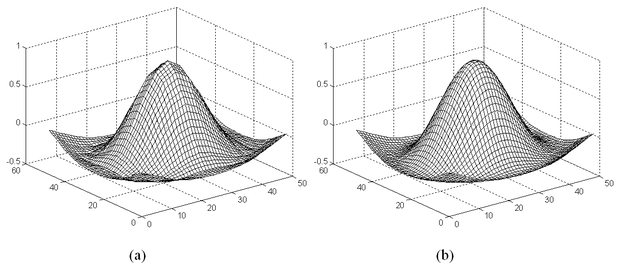
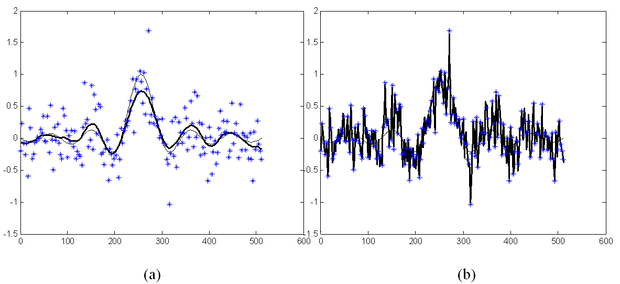
A tanítópontoktól eltérő bemenetekhez tartozó válaszok részletes elemzése a TA és B mátrixok vizsgálata alapján lehetséges. Ezek a mátrixok szabják meg, hogy a háló milyen interpolációs képességgel rendelkezik. A mátrixoknak, és különösen a B mátrixnak az elemzése általános esetben komoly nehézségekbe ütközik. Speciális esetben azonban, amikor a tanítópontok egyenletesen, egymástól pontosan t kvantumnyi távolságra helyezkednek el, a mátrixok analitikusan is felírhatók, és így a háló válaszai tetszőleges bemenethez analitikusan is meghatározhatók. A vizsgálat arra az eredményre vezet, hogy amennyiben a C / t arány egész, a háló a tanítópontok között lineárisan interpolál. Erre mutat példát az 5.12 (a) ábra. Természetesen a kvantálás hatását itt nem tekintjük, a lineáris interpoláció az egyes kvantumokhoz tartozó értékekre vonatkozik.
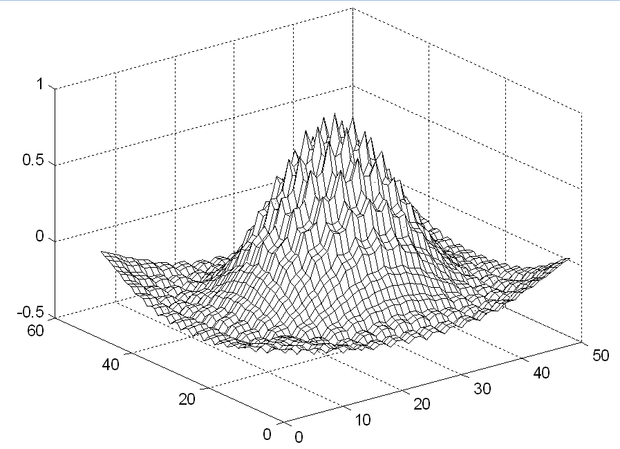
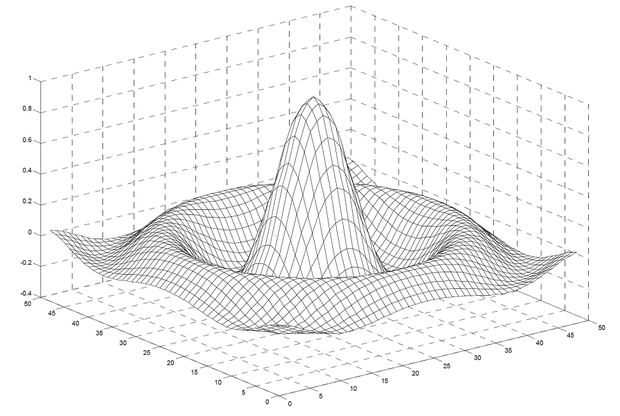
Ennél érdekesebb azonban, hogy egyéb esetekben, tehát ha a C / t arány nem egész szám, akkor a lineáris interpolációhoz képest jelentős eltérés lehet a válaszokban. Ez nyilvánvaló azokban az esetekben, amikor C < t, ugyanis a véges tartójú bázisfüggvények miatt ilyenkor található olyan súly, amelyet egyáltalán nem módosítunk a tanítás során. Ha C < t /2, az is előfordulhat, hogy egyes bemenetek csak olyan súlyokat választanak ki, melyek egyike sem módosul a tanításnál. Az ilyen bemeneteknél a háló válaszát a súlyok kezdeti értékei határozzák meg, tehát a válasznak semmi köze a tanítópontok által szolgáltatott információhoz. Az általánosítási hiba ezekre az esetekre analitikusan is könnyen származtatható. A nagy hiba miatt azonban a C < t tartománynak nincs gyakorlati jelentősége. A háló általánosítási képességénekvizsgálatából azonban az is kiderül, hogy még akkor is jelentős hiba léphet fel, amikor C > t . Ilyen esetet mutat az 5.12 (b) ábra, ahol a sinc(.) függvény CMAC-val történő approximációja látható C =8 és t =5 mellett.
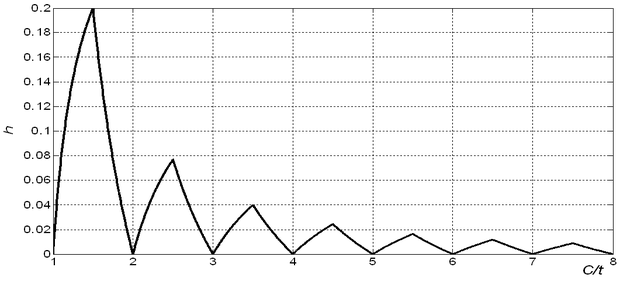
Az általánosítási hiba, pontosabban a válaszok lineáris interpolációtól való eltérésének a lineáris interpolációs válaszhoz viszonyított relatív hibája C > t mellett is felírható analitikusan. Ezt az értéket, amit relatív általánosítási hibának nevezünk, a következő összefüggés adja meg [Hor07]:
( 5 . 57 )
A fenti összefüggésben az egész rész függvény. A relatív általánosítási hiba alakulását mutatja az 5.13 ábra. E szerint a hiba akár 20% is lehet.
Ez a vizsgálat a tanítópontok egyenletes elhelyezkedése mellett érvényes. A gyakorlatban ritkán találkozunk ilyen esettel, a tanítópontok általában véletlen pozíciókban találhatók a bemeneti térben. A vizsgálat általánosítása tetszőleges pontelrendezésre azt mutatja, hogy kedvezőtlen esetben a relatív hiba még nagyobb is lehet, akár a 33%-ot is elérheti.
Többdimenziós esetben a helyzet bonyolultabb. Az egydimenziós esetnek megfelelő többdimenziós CMAC-t akkor kapnánk, ha a teljes, C N -szeres lefedést alkalmaznánk. Láttuk, hogy a komplexitás exponenciális növekedése miatt ez legfeljebb 2-3 dimenzióig lehetséges. A komplexitás csökkentését szolgálta a teljes lefedés helyett a bemenetek dimenziójától függetlenül alkalmazott C -szeres lefedés és a tömörítő leképezés. A tömörítő leképezés hatása megfelelően megválasztott tömörítő eljárás mellett közelítőleg elhanyagolható, a pontos hatás elemzése viszont meghaladja a jelen kereteket, ezért ezzel a kérdéssel nem foglalkozunk. (Meg kell azonban jegyeznünk, hogy a tömörítés mindenképpen gyengíti a háló képességeit, ezért ahol csak lehet, célszerű az alkalmazását elkerülni [Wan96], [Zho97]. A későbbiekben, a kernel gépekkel foglalkozó 6. fejezetben be fogjuk mutatni a CMAC olyan értelmezését, mely segítségével a tömörítő hash kódolás elkerülhető, anélkül, hogy a háló komplexitását extrém módon megnövelnénk.)
A háló approximációs képességéttöbbdimenziós esetben is a bemeneti réteg leképezése határozza meg. Itt is biztosítani kell, hogy az egymáshoz közeli bemeneti vektorok részben ugyanazokat a súlyokat válasszák ki, tehát, hogy a megfelelő memóriacímek részben azonosak legyenek. E követelményt teljesítő leképezés egy lehetséges megvalósításának elvét kétdimenziós bemenet esetére az 5.14 ábra mutatja, feltételezve, hogy a hálózat általánosító paramétere C =4.
Az ábrán nem a bázisfüggvények elhelyezkedését látjuk, hanem azt, hogy adott bemenet mellett mely bázisfüggvényekhez rendelt súlyok kiválasztása történik meg. A fekete pontok jelölik, hogy a bemeneti értékekhez hogyan rendelhetjük hozzá az asszociációs vektor aktív bitjeit. Minden egyes megjelölt fekete pont (rácspont) egy bitet képvisel az asszociációs vektorban (egy bázisfüggvényt képvisel), tehát ezekhez a pontokhoz kell a címeket hozzárendelnünk. Látható, hogy a kétdimenziós diszkrét mintatérben az egymástól C értékkel eltolt átlók rácspontjait használhatjuk fel. Az eljárás könnyen általánosítható N dimenzióra, ahol a megfelelő N- dimenziós C élhosszúságú hiperkockák testátlóinak rácspontjai képviselik az asszociációs vektor bitjeit. Az árnyékolt területek − melyek kétdimenziós bemeneteknél C × C -s négyzetek − különböző bemeneti vektorokhoz tartozó összerendelt rácspontokat és így az összerendelt címeket jelölik.
Az egymáshoz közeli bemeneteknél ( és ) most is lesznek közös címek, míg a kellő távolságban lévőknél ( és , illetve és ) ilyeneket nem találunk. Ugyanakkor az is látható, hogy a szükséges címek tartománya csak C =1 esetben egyezik meg a lehetséges diszkrét bemeneti vektorok számával, vagyis ilyenkor memóriacímre van szükség, ha az i -edik bemeneti komponens lehetséges értékeinek száma. C >1 esetben a címtartomány mérete csökken, minthogy ekkor az összes rácspont helyett csak a főátlóbeli és az ezzel párhuzamos, tőle kC értékkel ( k =1,2,…) eltolt mellékátlóbeli rácspontokhoz rendelünk asszociációs biteket.
Többdimenziós esetben a C -szeres lefedés azt eredményezi, hogy a tanítópontok számától függően az összefüggés jelenthet mind alulhatározott, mind túlhatározott egyenletrendszert. A -nak most is P sora van, hiszen P tanítópont áll rendelkezésünkre, az oszlopok számát (az asszociációs vektor hosszát) pedig az (5.52) összefüggés adja meg ( M C ). Mivel M C <<R és P ≤ R, M C és P viszonya bármi lehet. Az analitikus megoldást, a súlyvektor LS becslésétaz (5.55) összefüggés definiálja. Alulhatározott esetben most is végtelen sok megoldásunk lehet.
Iteratív tanításnál bármely, az A mátrix rangjának megfelelő számú tanítóponthoz tartozhat egy megoldás, melyek túlhatározott esetben ( P>M C ) különbözhetnek egymástól. Az egyes megoldások a megoldástérben egy tartományt jelölnek ki − melyet minimális konvergencia-tartománynak nevezhetünk. Ezen belül bármelyik érték kiadódhat attól függően, hogy mi a tanítópontok elővételi sorrendje és mekkora a tanulási tényező értéke. A tanulási eljárás közben, ha a tanítópontokat ciklikusan vesszük elő, a megoldás ebben a tartományban ciklikusan vándorol, megoldásként határciklust kaphatunk, míg véletlenszerű elővételnél a súlyvektor is véletlenszerű értékeket vesz fel, de a konvergencia-tartományból most sem lép ki. A pontonkénti tanításnál tehát ebben az esetben a súlymódosítás sohasem áll le. Batch tanításnál, ami megegyezik az analitikus LS megoldással, eredményként a minimális konvergencia-tartomány egy pontja adódik [Par92]. Túlhatározott esetben az analitikus LS megoldás és az iteratív LMS alapú megoldás nem feltétlenül azonos. Csak az biztos, hogy mindkét megoldás a minimális konvergencia tartományon belül van.
Többdimenziós esetben a bináris CMAC korlátozott approximációs képességgel rendelkezik. Ennek bemutatásához az 5.15 ábrán látható illusztrációt használhatjuk. Az ábra segítségével azt láthatjuk be könnyen, hogy a szomszédos cellák válaszai nem minden esetben lehetnek tetszőlegesek.
Vizsgáljuk meg a négy számozott elemi cella lefedését. Az 1. ( x 1 = j , x 2 = i +1) és a 2. cellánál ( x 1 = j +1, x 2 = i +1) a négy lefedő bázisfüggvény közül három azonos, csupán a negyedikben van eltérés. Ez azt jelenti, hogy a két bemeneti tartományhoz tartozó válaszok különbsége ennek a lefedésbeli különbségnek a következménye. A 3. ( x 1 = j , x 2 = i ) és a 4. ( x 1 = j +1, x 2 = i ) cellák lefedése között ugyanazt a különbséget találjuk, mint az előző két cellánál. Ebből adódóan a számozott cellákhoz tartozó válaszok nem lehetnek tetszőlegesek. A közöttük lévő kapcsolatot az ún. konzisztencia-egyenletfejezi ki [Bro93]:
, ( 5 . 58 )
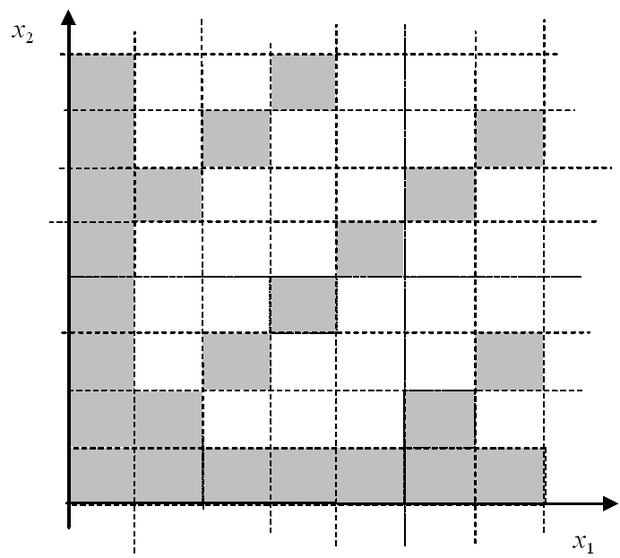
ahol y ( i ) az i- edik cella válasza. A konzisztencia-egyenlet szerint a négy szomszédos elemi cella mindegyikéhez nem rendelhetünk tetszőleges kívánt választ; a négy válasz közül három rögzítése megszabja, hogy milyen értéket tud a hálózat előállítani a 4. cellánál. Hasonló kapcsolat található az 5-8 számozású cellák válaszai között is és minden további, hasonló pozíciójú szomszédos cellanégyes között. Ez azt jelenti, hogy az elemi cellák mindegyikénél nem szabható meg a kívánt leképezés, ha azt szeretnénk, hogy a háló pontosan állítsa elő a kívánt válaszokat. A konzisztencia-egyenleteket végigterjesztve a teljes bemeneti tartományon látható, hogy a bemeneti celláknak csak egy, a C értékétől függő töredékén szabható meg a kívánt válasz szabadon. Ezt illusztrálja C =4 mellett az 5.16 ábra, ahol, ha az árnyékolt celláknál megszabjuk a kívánt válaszokat, a többi cella által előállítható válaszok kiadódnak.
Fentiek alapján látható, hogy a bináris CMAC egydimenziós bemenet mellett − a kvantálásból adódó hatásoktól eltekintve − a tanítópontokat hibátlanul képes megtanulni. Többdimenziós bemeneteknél azonban ez már nem igaz. Minél nagyobb C -t alkalmazunk, annál kevesebb diszkrét bemeneti értékhez rendelhetünk szabadon kívánt választ, annál több megkötést teljesítő leképezést képes csak a hálózat megvalósítani. A konzisztencia-egyenleteket tetszőleges C érték mellett csak az additív függvényosztály tagjai elégítik ki, vagyis csak olyan N -dimenziós leképezések valósíthatók meg pontosan, amelyek az alábbi formába írhatók:
( 5 . 59 )
Bár az függvények tetszőleges egyváltozós függvények lehetnek, az additív függvényosztályra való korlátozás modellező képesség tekintetében hátrány az univerzális approximátor MLP és RBF hálókhoz képest.
A háló által megvalósítható leképezésnek a konzisztencia-egyenletekben megfogalmazott korlátozása a bázisfüggvények számának növelésével gyengíthető, sőt teljes lefedésnél ez a korlátozás meg is szűnik. A bázisfüggvények számának növelése azonban komplexitási okokból erősen korlátozott. A klasszikus Albus-féle CMAC a bázisfüggvényeket az eddigiekben bemutatott módon a bemeneti tér fő- és mellék-átlóbeli rácspontjaihoz rögzíti, míg a teljes lefedés az összes rácsponthoz rendel bázisfüggvényt. A két határeset között bármilyen közbenső megoldás alkalmazható, tehát az Albus-féle megoldáshoz további bázisfüggvények adhatók. A hozzáadott bázisfüggvények számát elsősorban a komplexitás növekedése korlátozza. A többlet bázisfüggvények elhelyezésére pl. [Lan92]-ban találunk javaslatokat.
Az approximációs képességet anélkül is javíthatjuk, hogy a bázisfüggvények számát növelnénk. Ha a bázisfüggvények számát nem növeljük, a háló „szabadságfoka” nem nő, így a szabadon felvehető értékű mintapontok száma sem fog nőni. A szabadon felvehető és a kiadódó pontok elhelyezkedését azonban módosíthatjuk, elkerülve azt, hogy a kiadódó válaszok az 5.16 ábrán látható módon a bemeneti térben sávokban jelentkezzenek. Ez részben a tanításnál a tanítópontok elővételi sorrendjének megváltoztatásával, részben a bázisfüggvények elhelyezésének módosításával érhető el.
A véletlenszerű tanítópont elővételi sorrend az iteratív tanulásnál biztosíthatja, hogy a pontosan megtanulható pontok ne az ábrán látható szabályos elrendezés szerint helyezkedjenek el. A bázisfüggvények elhelyezésére [Bro94]-ben találunk javaslatot. Az eredeti Albus CMAC által alkalmazott lefedések a főátló pontjaihoz, mint referenciapontokhoz vannak rögzítve (ld. az 5.7 és az 5.15 ábrákat). Ha ezeket a referenciapontokat a bemeneti térben véletlenszerűen helyezzük el, a hiba „sávosodása” elkerülhető. Meg kell jegyezzük, hogy ez utóbbi két módszer az approximációs hibát nem szünteti meg, csak a bemeneti téren belül egyenletesebben osztja szét.
Látható, hogy approximációs képesség tekintetében lényeges különbség van az egydimenziós és a többdimenziós CMAC hálók között. Az általánosítási képességet tekintve, viszont többdimenziós esetben is hasonló viselkedést tapasztalunk, mint egydimenziós esetben. Amennyiben a tanítópontok egyenletes t osztástávolságú rácson helyezkednek el és C / t=l egész szám, a tanítópontok közötti lineáris interpoláció adja meg a háló válaszát. Erre mutat egy példát az 5.17 ábra. Az (a) ábrán a kétdimenziós sinc függvény egy szegmensének CMAC-vel történő approximációját látjuk C = t =4 beállítás mellett. Az eredeti függvény a (b) ábrán látható (az ábrán a kvantálás hatásától most is eltekintünk).
Ha C / t ≠ l , az egydimenziós esethez hasonlóan igen jelentős általánosítási hiba léphet fel. Az előző feladat megoldása C =4 és t =3 mellett látható az 5.18 ábrán.
A nagy általánosítási hiba oka − ha C / t arány nem egész szám − az, hogy a súlyok nagyon különböző értéket vesznek fel még akkor is, ha a kívánt válaszok minden tanítópontban azonosak. A különböző értékek azért alakulnak ki, mert az egyes súlyoknál a módosítások száma eltérő. A súlymódosítások száma minden súlynál csak akkor lesz azonos, ha C / t egész szám. Ezt egydimenziós esetben könnyű belátni. Tekintsük azt az esetet, amikor C / t= 1. Mivel a C tartójú bázisfüggvények miatt minden tanítópont C szomszédos bázisfüggvényt aktivizál és tanításnál az ezekhez tartozó súlyokat módosítjuk, nem lesz olyan súly, melyet több tanítópont is ki fog választani. Minden tanító lépésben más és más C súly módosítására kerül sor úgy, hogy a tanítópontok egyszeri felhasználása során minden súlyt egyszer és csakis egyszer módosítunk. Mivel az egy tanítóponthoz tartozó C súly módosítása azonos mértékű (ld. az LMS algoritmus megfelelő összefüggését), ha a kezdeti értékek azonosak voltak, az egy tanítópont által kiválasztott C súly azonos értékű lesz egy teljes tanítási ciklus, epoch után is. Hasonló súlyeloszlást kapunk, ha C / t = l , ahol l ≥ 2 egész. A különbség mindössze annyi, hogy most minden súlyt pontosan l -szer fogunk módosítani. Ezzel szemben, ha a C / t arány nem egész, a módosítások száma egyes súlycsoportoknál eltérő lesz, ami eltérő súlyértékeket is eredményez.
A fenti hatás mérséklése lehetőséget ad a nagy általánosítási hiba csökkentésére. Olyan módon kell módosítani a tanulási eljárást, hogy a tanítópontokban fellépő hiba redukciója mellett azt is biztosítsuk, hogy az egy tanítóponthoz tartozó súlyok minél inkább egyformák legyenek. Az eljárást a következő részben mutatjuk be.
Mivel a CMAC csak a kimeneti lineáris rétegben tartalmaz tanítható súlyokat, ezek meghatározása az előzőek szerint vagy analitikusan, vagy iteratív eljárással, leggyakrabban az LMS algoritmus alkalmazásával történhet. A hálózat speciális kialakítása miatt azonban még az LMS algoritmus is egyszerűsödik.
A hálózatban a kimeneti réteget kivéve csak bináris értékek találhatók, a bemeneti nemlineáris leképezést megvalósító rész tisztán digitális hálózat: a kvantált bemenetek bináris reprezentációjából az asszociációs vektor ritka bináris reprezentációját állítja elő. Mivel a kimeneti réteg bináris bemenetekkel dolgozik, tényleges szorzásra a hálózatban nincs is szükség. A súlymódosítás az LMS algoritmus szerint
, ( 5 . 60 )
ahol a i ( k ) a k -adik bemenethez tartozó asszociációs vektor i -edik bitje. Tehát az asszociációs vektor aktív bitjei által kiválasztott C súlyt azonos mértékben kell módosítani. A módosítás mértéke pedig a hiba, valahányad, célszerűen kettő negatív egész hatványad része. Így tehát nemcsak a háló kimeneti értékének kiszámításához − a visszahívási fázishoz −, hanem a tanításhoz sem szükséges szorzás. Ez a tulajdonság a hálózatot különösen alkalmassá teszi a digitális VLSI megvalósításra, lehetővé téve így a nagysebességű parallel implementációt [Mil91].
További előny a CMAC hálózat ún. inkrementális tanulásiképessége. Ennek oka, hogy hasonlóan az RBF hálózathoz a tanítópontok hatása csak korlátos bemeneti tartományra terjed ki, a hálózat lokális általánosító-képességgel rendelkezik. Míg azonban az RBF hálónál valójában nem lokális tartójú bázisfüggvényeket használunk, itt ténylegesen véges ( C kvantum oldalhosszúságú hiperkocka) a bázisfüggvények tartója Egy tanítóponttól nagyobb távolságra a leképezés kialakításában e pontnak nincs hatása, vagyis az egymástól távolabbi bemeneti tartományokhoz tartozó válaszok egymástól függetlenül alakíthatók ki. Egy tanító lépésben a kimeneti réteg súlyainak csak a töredéke − maximum C súly − módosul, vagyis az egymástól távol lévő tanítópontok a hálózat súlyainak eltérő, egymástól független csoportjaira hatnak, szemben a globális általánosító-képességgel rendelkező többrétegű perceptronnal, ahol minden tanító lépésben az összes súly módosul.
A hálózat lényeges jellemzője a viszonylag gyors tanulás. A gyorsaság azt jelenti, hogy hasonló méretű feladat MLP és hibavisszaterjesztéses eljárás feltételezésével csak nagyságrendekkel több tanító lépés alatt oldható meg, mint CMAC hálózattal. A nagyobb sebesség részben a lokális tanulás következménye − ezért általában viszonylag kevés iterációs lépésre van szükség −, részben abból adódik, hogy egyszerű műveletekre van csak szükség. A hálózat leggyorsabban akkor tanítható, ha módunk van a tanítópontok olyan megválasztására, hogy az összes tanítópont egyszeri felhasználásával minden súlyt módosítsunk, de mindegyiket csak egyszer. Az előbbiekben láttuk, hogy ez egydimenziós bemenetnél akkor érhető el, ha a tanítópontok pontosan C kvantumnyi távolságban vannak egymástól, így az egyes tanítópontok mindig másik C elemű súlykészletet módosítanak. Ebben az esetben nemcsak az érhető el, hogy a súlyokat egy tanítási ciklusban ki tudjuk alakítani, hanem az is, hogy a hálózat válasza minden tanítópontban megegyezik a kívánt válasszal, a tanítópontok közötti közbenső bemeneti értékekre adott válaszok pedig a szomszédos válaszok közötti lineáris interpoláció eredményeként adódnak, ahogy ezt az általánosítóképesség vizsgálatánál láttuk. A tanítópontok egyszeri felhasználása – egyetlen epoch – akkor ad hibátlan eredményt, ha megfelelő tanulási tényezőt alkalmazunk. Ez a fenti tanítópont elrendezésnél μ =1/ C mellett lehetséges.
A tanulási szabály módosítása, súlykiegyenlítő regularizáció
Az általánosítási hiba okainak elemzése azt mutatta, hogy a hiba csökkentése lehetséges, ha a tanítás során törekszünk arra, hogy az egyszerre kiválasztott súlyok minél inkább azonosak legyenek. Ezt úgy érhetjük el, hogy a kritériumfüggvényt kiegészítjük egy olyan taggal, mely ezt a járulékos feltételt kényszeríti rá a súlyokra. A megoldás egy regularizációseljárás, ahol a kritériumfüggvény a szokásos négyzetes tag mellett egy regularizációs tagot is tartalmaz:
( 5 . 61 )
Látható, hogy a regularizációs tag azt fogalmazza meg, hogy az egy bemenethez tartozó súlyok értékei minél inkább a d / C értéket vegyék fel, ahol d az adott bementhez tartozó kívánt válasz. Azonos súlyértékeket általános esetben nyilván nem kaphatunk, hiszen ekkor a tanítópontokban kapnánk nagy hibát. A két tag egyensúlyát a λ regularizációs együttható megfelelő megválasztásával biztosíthatjuk.
A fenti kritériumfüggvénynek megfelelő iteratív, gradiens alapú tanító eljárás a következő:
( 5 . 62 )
A kapott tanulási szabályt súlykiegyenlítő, vagy súlysimító regularizációs szabálynak nevezzük, ahol a két tag arányát μ és λ megválasztásával állíthatjuk be. A regularizációs eljárás hatása az 5.19 és az 5.20 ábrán látható.
Az előbbi egy egydimenziós, az utóbbi egy kétdimenziós sinc függvény esetén mutatja a háló válaszát C =4, t =3 értékekre. Az 5.19 (a) ábrán a regularizált változat válasza látható; az összehasonlításhoz a (b) ábrán az eredeti Albus változat válaszát is megadtuk. Látható, hogy regularizált esetben a válasz nemcsak sokkal simább, hanem az approximáció átlagos négyzetes hibája is jelentősen csökkent.
Az 5.20 ábra kétdimenziós mintapéldája is azt mutatja, hogy az 5.18 ábrán látható jellegzetes CMAC válasz helyett sima választ kapunk.
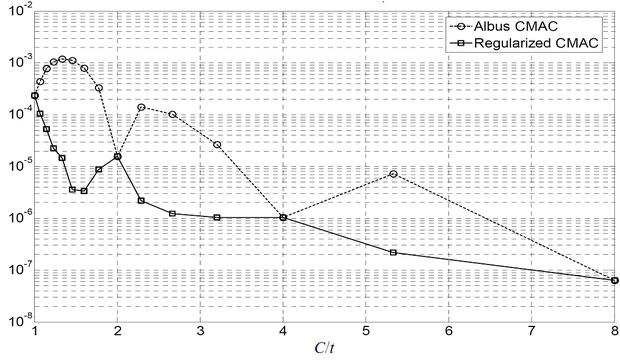
A súlykiegyenlítő regularizációnakaz általánosítási hibát csökkentő hatását mutatja az 5.21 ábra, ahol a C / t arány függvényében az approximáció átlagos négyzetes hibáját adjuk meg az eredeti és a regularizált tanítás mellett az egydimenziós sinc függvény tanításánál. A hiba − ahogy vártuk − a kétféle tanító eljárás mellett a C / t arány egész értékeinél azonos, köztük viszont a regularizált esetben sokkal, egyes tartományokban akár több nagyságrenddel is kisebb. Sőt az is látszik, hogy regularizált esetben még akkor is jobb megoldást kaphatunk, mint regularizáció nélkül, ha közben a tanítópontok számát csökkentjük ( C / t arányt növeljük). Az ábra konkrét esetre adja meg az approximációs hiba értékét, az eredmény azonban jellegre általánosan is érvényes.
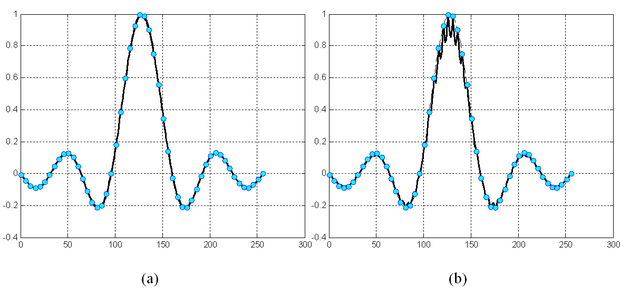
A regularizáció hatását zajos tanítópontok mellett mutatja az 5.22 (a) ábra. Összehasonlításként az 5.22 (b) ábrán a klasszikus Albus CMAC válasza látható azonos tanítópont-készlet és háló paraméterek mellett. Amint az várható az Albus CMAC-nál a tanítópontokban a válasz hibátlan, ami zajos esetben kimondottan káros. A tanítópontokra való tökéletes illeszkedés − ahogy ezt az előzőekben már bemutattuk − egydimenziós esetben az eredeti CMAC alaptulajdonsága a szabad paraméterek nagy száma miatt. A szabad paraméterek számának korlátozása, vagy valamilyen simasági mellékfeltétel figyelembevétele a háló eredő approximációs képességeit javítja.
Az elmúlt több mint 30 évben a CMAC hálózatoknak igen sok változata alakult ki. Ezek a változatok olyan módosítások eredményeként születtek, melyek egyrészt a háló képességeinek javítását, másrészt a többdimenziós eset extrém nagy komplexitásának csökkentését célozzák. A következőkben előbb az ún. magasabbrendű CMAC hálózatokkal foglakozunk, majd néhány olyan strukturális változtatást mutatunk be röviden, melyek a súlyok számának drasztikus csökkentését úgy próbálják elérni, hogy közben a háló teljesítőképessége ne romoljon.
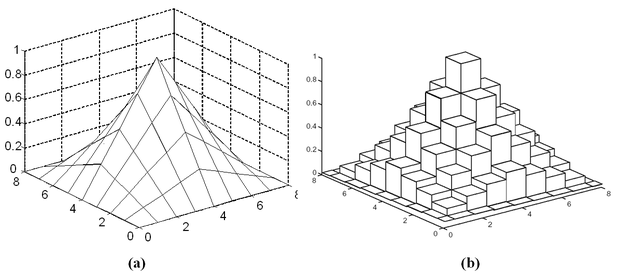
Az eredeti Albus-féle CMAC hálózat bináris bázisfüggvényeket használ, vagyis ezen bázisfüggvények értéke bármely olyan bemenetre, amely az érzékelési mezőbe esik 1, míg az összes többi bemenetre 0. A bináris bázisfüggvény következménye az egyszerű realizálhatóság − a szorzó nélküli struktúra −, de részben ennek a következménye a korlátozott modellező képesség is. Magasabbrendű CMAC hálózatnál a négyszögletes függvény helyett lineáris, kvadratikus, stb. bázisfüggvényeket használunk. Az egyváltozós lineáris bázisfüggvény a következő:
, ( 5 . 63 )
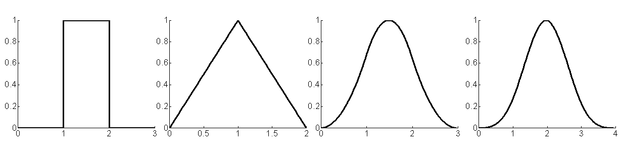
ha t a C szélességű bázisfüggvény középpont paramétere. Ezek a bázisfüggvények a B-spline függvénycsalád elemeinek is tekinthetők. A bináris bázisfüggvény az elsőrendű, a lineáris a másod-, a négyzetes a harmad-, stb., és a ( k -1)-ed fokú polinommal létrehozott a k -ad rendű B-spline függvény . Az 5.23 ábra k =1, 2, 3, 4 esetre mutatja az első néhány B-spline függvényt. A B-spline függvények előnye a könnyű előállíthatóság és az, hogy egy k -ad rendű B-spline ( k -1)-szer deriválható.
A k -ad rendű B-spline bázisfüggvény az elsőrendű B-spline függvény önmagával vett k -szoros konvolúciója útján állítható elő. Ha a bemeneti tartományt kvantáljuk, a kvantált intervallumokhoz hozzárendelt B-spline függvényértékek a következő rekurzív összefüggések alapján is számíthatók:
( 5 . 64 )
ahol I j =( λ j -1 λ j ] a j -edik bemeneti intervallum.
N -változós bázisfüggvény az egyváltozós függvények szorzataként nyerhető:
( 5 . 65 )
A lineáris bázisfüggvényt (másodrendű B-spline-nak megfelelő) kétdimenziós esetre az 5.24 ( a) ábra mutatja.
Bár a magasabbrendű bázisfüggvények alkalmazása a modellező képességet javítja, a kvantált bemenet miatt a háló által megvalósított leképezés szakaszosan konstans tulajdonsága megmarad, ugyanis egy bemeneti cellán (kvantumon) belül, bármely bemeneti értékhez egyetlen asszociációs vektor és ennek megfelelően konstans válasz tartozik. A modellező képesség azon hiányossága, hogy a háló a kvantált bemenetek miatt a folytonos bemenet függvényében szakaszosan konstans leképezést valósít meg sok esetben nem jelent hátrányt, hiszen a bemeneti mintáink úgyis digitalizált formában állnak rendelkezésre (pl. digitális szabályozási feladatok esetén).
Ekkor a ténylegesen alkalmazott bázisfüggvény az 5.24 (a) ábrán látható helyett a (b) ábrán bemutatott lépcsős függvény lesz. Ennek ellenére már az elsőrendű bázisfüggvény alkalmazása is biztosítja, hogy a CMAC háló ne csak az additív függvényosztály elemeinek megvalósítására legyen alkalmas.
Amennyiben mégis analóg bemenetekkel dolgozunk, a kvantálás hatásának kiküszöbölésére több lehetőségünk is van. A magasabbrendű bázisfüggvények alkalmazása lehetővé tenné a folytonos leképezés megvalósítását akkor, ha egy bemeneti cellához nem konstans függvényértéket, vagyis nem lépcsős függvényt rendelnénk. Ez azt jelenti, hogy pl. kétdimenziós bemenet és lineáris bázisfüggvény mellett valóban az 5.24 (a) ábrán látható bázisfüggvénnyel dolgoznánk. Az így kapott B-spline [Lan92] bázisfüggvényekkel a folytonos leképezés megvalósítható, sőt nemcsak a függvényértékek, hanem a függvény bizonyos deriváltjai is előállíthatók: k-ad rendű B-spline bázisfüggvények alkalmazásával a (k-1)-edik deriváltakig bezárólag a függvény differenciálhányadosai is approximálhatók. E megoldás fő nehézsége a bázisfüggvényértékek meghatározásának nagyobb számításigénye, valamint az, hogy a bináris CMAC hálók egyik legfontosabb előnyét, nevezetesen, hogy sem a tanítási, sem a visszahívási fázisban nem igényelnek szorzást elveszítjük. A lépcsős bázisfüggvények mellett jóval kisebb a számításigény és jóval hatékonyabb hardver struktúra alakítható ki, mint a folytonos függvények alkalmazásakor [Hor98], [Ker95]. Alkalmazástól függ, hogy a nagyobb számításigényű magasabbrendű, esetleg folytonos változat, vagy az egyszerűbb, de korlátozott képességekkel rendelkező eredeti változat mellett döntünk.
Folytonos leképezés lépcsős bázisfüggvények mellett a kvantálásnál szokásos egyenletes eloszlású additív zaj ( dither ) [Lip92] alkalmazásával valósítható meg. Ennek ára, hogy visszahívási fázisban egy bemenetet nem egyszer, hanem többször, különböző additív zaj értékek mellett kell a hálózatra adni és a kimenetek átlaga adja a tényleges választ.
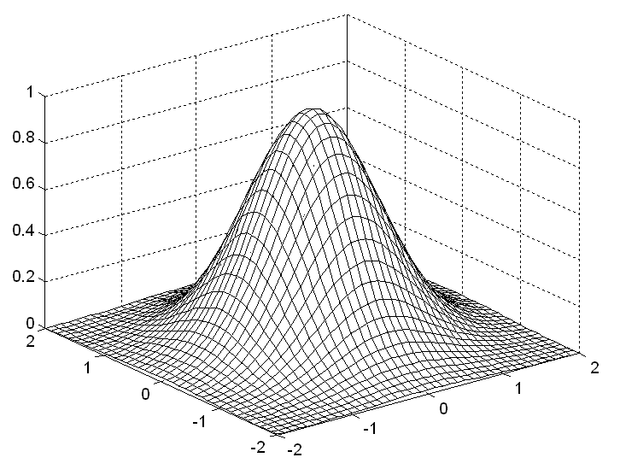
A magasabbrendű változatok között megtalálható a Gauss függvényes megoldás is, amely egy olyan k -ad rendű B-spline bázisfüggvényes hálónak felel meg, ahol k elég nagy. Ugyanis k növelésével a B-spline függvények tartanak a Gauss függvényhez; k > 6 esetén a közelítés már igen jó. Gauss bázisfüggvényekkel a CMAC az RBF-hez hasonló, azzal az eltéréssel, hogy megtartjuk a CMAC-ra jellemző felépítést, vagyis a bázisfüggvények elhelyezési rendszerét és azt, hogy a bázisfüggvények véges tartójúak. Gauss-CMAC hálóknál a tartó most is egy C kvantumnyi oldalhosszúságú hiperkocka (5.25 ábra).
A háló képességeit a tanuló eljárás módosításával is javíthatjuk. A kredit-hozzárendeléses tanításnál egy tanító lépésben a kiválasztott C súly módosítása nem azonos mértékű. Az egyes súlyokhoz hozzárendelt kredit attól függ, hogy az adott súlyt előzőleg hányszor módosítottuk. Minél többször módosítottunk egy súlyt, annál kisebb mértékben fogjuk a további tanítási ciklusokban módosítani. A CA-CMAC tanítási összefüggése:
( 5 . 66 )
ahol f i az i -edik súly eddigi módosításainak száma, az összefüggés pedig az i -edik bázisfüggvényhez (a w i súlyhoz) rendelt kredit érték.
A CA-CMAC eljárás [Su03] hatása részben hasonló a súlykiegyenlítő regularizáció hatásához. Egyrészt simább választ eredményez, másrészt a tanítást gyorsíthatja is.
A többdimenziós CMAC esetenként extrém komplexitású lehet, annak ellenére, hogy a válaszok számításához csak a súlyok tárolására és egyszerű műveletek elvégzésére van szükség. A szükséges memória mérete azonban megvalósíthatatlanul nagy is lehet (a dimenzió átka probléma), ezért ennek redukálása az alkalmazhatóság előfeltétele. Az Albus által javasolt hash kódolás ugyan jelentősen csökkenti a súlymemória méretét, de az említett ütközések a tanítás konvergencia tulajdonságait rontják, annak ellenére, hogy az ütközések valószínűsége igen kis értékre szorítható [Wan96], [Zho97].
Hash kódolás helyett a súlymemória méretének csökkentésére több lehetőségünk van. Egyrészt egy N -változós CMAC dekomponálható kisebb dimenziós CMAC hálózatokra, melyek eredményeit valamilyen módon összesíteni kell, másrészt a CMAC-nál is alkalmazható az ún. kernel trükk, mely a problémát a bázisfüggvények teréből egy ún. kernel térbe transzformálja. A kernel térben a probléma komplexitása dimenziótól függetlenül a tanítópontok száma által korlátozott. Az így született kernel-CMAC-t a kernel gépeknél, a 6. fejezetben mutatjuk be. A kisebb-dimenziós hálózatokra történő dekomponálás fő eredményeit itt foglaljuk össze.
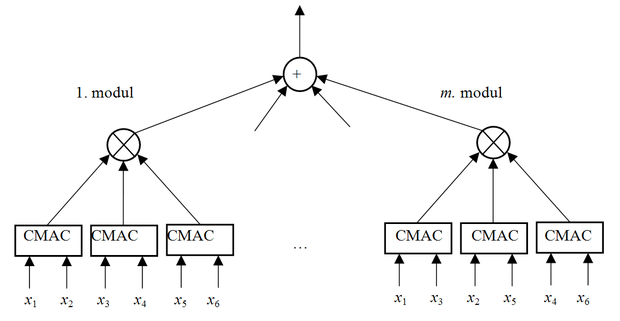
Egy N -változós CMAC komplexitását igen hatékonyan redukálhatjuk, ha dekomponáljuk egy- vagy kétváltozós hálókra, majd ezek eredményeit egyesítjük, hogy az eredő háló az eredeti N -változós feladat megoldását adja. A dekomponálásra több lehetőségünk is van. Ezek egyike az ún. szorzatok összege ( sum-of-product , SOP) struktúra, amely egy olyan moduláris architektúra, ahol egy- vagy kétváltozós hálók kimeneteinek szorzata képezi egy modul kimenetét.
A teljes hálót több ilyen modul összegeként kapjuk meg. A modulok számát a tanulási eljárás részeként határozhatjuk meg fokozatos bővítés útján. Ha adott számú modul összegeként kapott eredő válasz hibája még nem elegendően kicsi, további modult alakítunk ki, melyet szintén integrálunk az eddigi hálózatba. Ha egyváltozós elemi CMAC hálókból építkezünk, minden modulban mind az N bemeneti változóhoz rendelünk egy egydimenziós hálót. Ha az elemi hálók kétdimenziósak, minden modul más-más kétdimenziós CMAC hálók szorzatát képezi [Lin96], [Li04]. A szorzatok összege struktúra kétdimenziós elemi hálókkal az 5.26 ábrán látható.
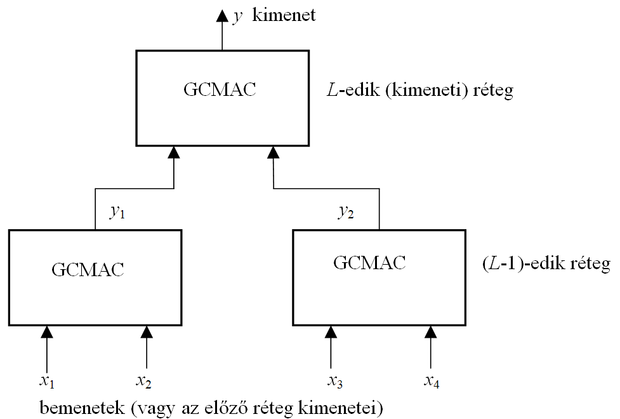
A HCMAC háló ugyancsak kétváltozós elemi hálókat alkalmaz, és egy hierarchikusbináris fa struktúrát épít fel [Lee03]. Itt az elemi kétváltozós hálók kimeneteit is kétváltozós CMAC hálók dolgozzák fel tovább, tehát egy többszintű hálóarchitektúra jön létre. N -változós bemenetek mellett log 2 N hierarchia szintre van szükség. Az egyes kétváltozós CMAC hálók Gauss bázisfüggvényekkel dolgoznak, ahol a bemeneti teret folytonosnak tekintjük. A Gauss bázisfüggvények elrendezése ettől függetlenül követi az Albus-féle bázisfüggvény elrendezést, ahogy ezt az 5.15 ábra mutatja. A hierarchikus architektúra miatt minden egyes rétegben találunk tanítandó paramétereket, a kétdimenziós CMAC súlyait. Ezek tanítása a hibavisszaterjesztéses algoritmus alkalmasan módosított változatával lehetséges. A háló architektúráját az 5.27 ábra adja meg. Az ábrán GCMAC a Gauss bázisfüggvényekkel dolgozó hálókat jelöli.
A dekompozíció egy más formáját alkalmazza az MS-CMAC háló [Hun99], [Hun01]. Az N -változós hálót itt úgy bontjuk fel egy egyváltozós hálókból építkező hierarchikus architektúrára, hogy az egyes hálókat egymástól függetlenül lehessen tanítani. A háló az egydimenziós elemi CMAC hálók esetében megtartja az eredeti Albus-féle felépítést, úgy, hogy egy hierarchiaszinten az N változóból csak egynek az értéke változhat, míg a maradék N -1 értéke rögzített. Ez azt jelenti, hogy az első hierarchia szinten, a bementi rétegnél csak egy változó, pl. x 1 a valódi bemeneti változó, és annyi egydimenziós hálót kell felépíteni, ahány rögzített értéket a tanítópontokban felvehet a maradék N -1 változó: x 2 , …, x N . Láthatóan ez a megoldás kihasználja, hogy a bemenetek kvantáltak, de a kvantálás nem lehet nagyon finom, különben az egydimenziós hálók száma nagyon nagy lehet. Pl. egy 3-bemenetű hálónál, ha a tanítópontoknál az egyes bemeneti komponensek csupán 10-10 diszkrét értéket vehetnek fel, az első rétegben 100, a másodikban 10, a harmadikban pedig 1 egydimenziós CMAC hálóra van szükség.
Bár összességében az így megvalósított N -dimenziós CMAC jóval kevesebb súlyt igényel, mint az eredeti verzió, nagy bemeneti változószám és finomabb felbontás mellett ez is elfogadhatatlanul nagy memória-komplexitású megoldásra vezet. Ráadásul további korlátozásoknak kell eleget tenni: a háló csak akkor tanítható, ha a tanítópontok egy szabályos rács pontjain helyezkednek el. A háló válasza bármely diszkrét érték mellett meghatározható, de ha a tanítópontok közötti bemenetekre adott válaszokat akarjuk megkapni, a bemeneti réteg kivételével a többi réteg elemi CMAC hálóinál visszahíváskor be kell iktatni egy tanítási fázist is.