5.1. Az RBF (Radiális Bázisfüggvényes) hálózat
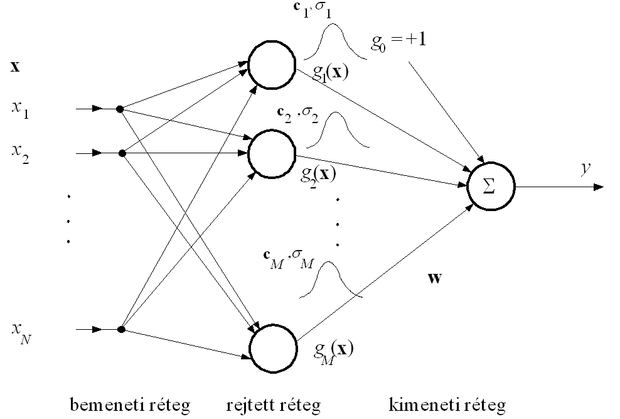
Az RBF hálózat olyan két aktív rétegű előrecsatolt hálózat, melyben a rejtett réteg radiális bázisfüggvényekkel dolgozó nemlineáris leképezést valósít meg. A háló felépítése az 5.2 ábrán látható.
A hálóban az első rétegbeli processzáló elemek valósítják meg a bázisfüggvényeket. Az RBF hálóknál ezek gömbszimmetrikus függvények. Az egyes processzáló elemekhez általában két paraméter tartozik, melyek a bázisfüggvények középpont- és szélességparaméterei. A rejtett réteg processzáló elemei minden bemeneti vektorhoz eltérő paraméterekkel rendelkező bázisfüggvény-értékeket rendelnek, a kimeneti processzáló elemek pedig ezen függvény-értékek lineáris kombinációit határozzák meg. Ha x a hálózat bemeneti vektora, g (.) jelöli a radiális bázisfüggvényt, pedig az i -edik processzáló elemhez tartozó függvény középpont-paraméterét, akkor az RBF hálózat által megvalósított leképezés a következő formába írható:
. ( 5 . 1 ’)
Ez azt jelenti, hogy a rejtett réteg minden processzáló eleme előbb meghatározza a bemeneti vektornak a processzáló elemhez rendelt középpont-paramétertől való távolságát, majd e távolságérték valamely nemlineáris függvényét számítja ki.
Az RBF hálózat szintén képes függvényapproximációra. Mint az 1.4. szakaszban láttuk (ld. 1.6. tétel), megfelelően megválasztott g (.) függvény és alkalmas és paraméterek mellett a hálózat tetszőleges folytonos függvény tetszőleges pontosságú approximációjára képes, ha a rejtett réteg mérete, a bázisfüggvények száma megfelelő. Az approximáció valójában úgy történik, hogy a tanítópontokra vagy a tanítópontokból valamilyen módon kialakított ún. klaszterközéppontokra bázisfüggvényeket illesztünk, és ezen bázisfüggvények lineáris kombinációját határozzuk meg. A bázisfüggvények legtöbbször a
( 5 . 2 )
Gauss függvények, de más bázisfüggvény is választható. Szokásos további függvények pl:
|
|
(szakaszonkénti lineáris approximáció) | |
|
|
(köbös approximáció) | |
|
|
0< β <1 |
( β =1/2-nél multikvadratikus függvény) |
|
|
α >0 |
( α =2-nél inverz multikvadratikus függvény), |
ahol c >0 és , melyben a értékek az alkalmasan megválasztott középpontok.
Az RBF hálók konstrukciója a háló méretének (a rejtett rétegbeli elemek számának), a bázisfüggvények paramétereinek (amennyiben vannak a bázisfüggvényeknek szabad paraméterei) és a kimeneti réteg súlyainak meghatározását jelenti.
A hálózat komplexitása a rejtett rétegbeli processzáló elemek számától, vagyis az eltérő középpontú bázisfüggvények számától függ. A középpontok számának meghatározása azonban nem független a középpontok helyzetének megválasztásától. A két kérdést tehát együttesen kell vizsgálni.
Gauss bázisfüggvények esetén a középpontokon kívül az ún. szélességparaméterekre ( ) is szükség van. A értékekre azonban az approximáció kevéssé érzékeny, ezért ezek széles határok között megválaszthatók. Legtöbb esetben a szélességparaméter minden rejtett processzáló elemre azonos, vagyis .
A rejtett rétegbeli processzáló elemek paramétereit és a kimeneti réteg paramétereit eltérő módon választjuk meg, ill. határozzuk meg. A kimeneti réteg paraméterei, a súlyok vagy analitikus úton meghatározhatók, vagy ellenőrzött tanítás során alakíthatók ki. A bázisfüggvény paramétereinek (a és esetenként a értékeknek) a megválasztására különböző eljárásokat alkalmazhatunk.
A bázisfüggvények számának és a középpont paramétereknek a meghatározása a tanítópontok számától is függ. Kevés tanítópont esetén triviális megoldás lehet, ha minden egyes tanítópont egyben függvényközéppont is lesz, vagyis a rejtett rétegben a processzáló elemek száma megegyezik a tanítópontok számával. A kimeneti lineáris réteg tanítása ilyenkor − ahogy ezt a lineáris elemi neuron, az adaline tanításánál láttuk − egy olyan lineáris egyenletrendszer megoldását jelenti, ahol az egyenletek száma és az ismeretlenek száma megegyezik. Itt tehát analitikus megoldás is nyerhető. Ha az x i tanítópontokra adott kívánt válaszokat most is , i =1, 2, ..., P jelöli, akkor a megoldandó egyenlet:
, ( 5 . 3 )
ahol a G az ún. interpolációs mátrix (a bázisfüggvények által megvalósított leképezések P × P -s mátrixa) és d a kívánt válaszokból álló oszlopvektor. A kvadratikus mátrix elemei: . Amennyiben G nem szinguláris a megoldásvektor létezik:
. ( 5 . 4 )
A gyakorlatban (5.4) megoldása nehézségekbe ütközik, ha G közel szinguláris. Ebben az estben a regularizáció elmélet (ld. 2.1. szakasz) segítségével juthatunk a megoldáshoz. A regularizáció során a G mátrix helyett a G + λ I perturbált mátrixot alkalmazzuk, ahol λ a regularizációs együttható, melynek már igen kis értéke mellett is biztosított, hogy a perturbált mátrix invertálható lesz. A regularizáció valójában azt jelenti, hogy a összefüggés helyett egy összefüggés megoldását keressük, vagyis olyan súlyokat keresünk, melyekkel a háló leképezése a tanítópontokban sem lesz pontos, tehát ott sem fog a kívánt válaszokkal megegyező kimeneteket előállítani. Az eltérés függ a regularizációs együttható értékétől. A regularizáció azáltal, hogy a tanítópontokban is megenged eltérést a kívánt válaszoktól, valójában egy simább leképezést megvalósító hálót eredményez. A regularizáció és a simaság kapcsolatáról a későbbiekben, a kernel gépeknél (6. fejezet) még lesz szó.
Az analitikus megoldáshoz az összes tanítópont ismeretére szükség van, és a megfelelő mátrix invertálási műveletet el kell végezni. A mátrix invertálás elkerülhető, ha pontonkénti iteratív tanítást (pl. LMS eljárást) alkalmazunk.
Nagyszámú tanítópont mellett minden tanítópont középpontként való felhasználása nem alkalmazható, hiszen ekkor sok rejtett processzáló elemet tartalmazó, igen nagy hálót is nyerhetünk. Ez egyrészt a szükséges számítások mennyiségét nagyon megnövelné, másrészt a sok processzáló elem szükségtelen is.
Amennyiben a tanítópontoknak csak egy részéhez rendelünk bázisfüggvényeket, akkor részint a megfelelő súlyértékeket az előbbiekben bemutatott megoldástól némileg eltérő módon nyerjük, részint meg kell adnunk a középpontként felhasználandó tanítópontok kiválasztási eljárását.
Ha a mintapontok száma, P nagyobb, mint a bázisfüggvények száma, vagyis a meghatározandó súlyok száma, M, a G mátrix nem lesz kvadratikus. P>M esetében túlhatározott egyenletrendszerrel van dolgunk és analitikus megoldást LS értelemben a pszeudo-inverz meghatározásával a (3.23) összefüggésnek megfelelően nyerhetünk:
( 5 . 5 )
Előfordulhat, hogy a G T G mátrix nem invertálható, lehet szinguláris vagy közel szinguláris akár numerikus problémákból adódóan. Ekkor itt is a regularizáció alkalmazható:
( 5 . 6 )
A megoldást iteratív úton most is meghatározhatjuk az LMS algoritmus alkalmazásával. Túlhatározott egyenletrendszer esetén a pontonkénti tanulásnál azonban nem kapunk egyértelmű megoldást. Meghatározható egy olyan tartomány, melyen belül kell legyen a megoldásvektor. A tartományon belüli konkrét megoldás, azonban függ a tanítópontok sorrendjétől és a tanulási tényezőtől is.
A középpontok kiválasztásának, illetve meghatározásának néhány lehetőségével a következő részben foglakozunk.
A középpont kiválasztó eljárások célja minden esetben az, hogy az összes tanítópontnál kevesebb bázisfüggvénnyel oldjuk meg a feladatot és ezen bázisfüggvények középpont paramétereit valamilyen módon a tanítópont-készlethez igazodóan meghatározzuk. A középpont kiválasztó eljárások nagy mintapontszám mellett biztosítják, hogy megvalósítható méretű hálóhoz jutunk.
Nagy mintapontszám több esetben is előállhat. Egyrészt rendelkezésünkre állhat nagyon nagyszámú − több tízezer, vagy akár több százezer − tanítópont is, melyek mindegyikét nem lehet és nem is szükséges felhasználnunk. Elegendő egy megfelelő részhalmaz kiválasztása és ennek felhasználásával ún. ritka ( sparse ) megoldás létrehozása. Ebben az esetben a tanító készletünk tulajdonképpen redundáns, így valójában információvesztés nélkül lehet a tanítópontok közül egy részhalmazt kiválasztani: a középpontokat egyszerűen a tanítópontokból véletlenszerűen kiválasztott K pont képezi.
Az is lehetséges, hogy a tanítópontok egyes csoportjaihoz rendelünk középpontokat. Ekkor valójában a pontok klaszterezését kell elvégeznünk. A tanítópontok csoportosítására, klaszterek képzésére bármilyen klaszter kialakító algoritmus használható.
Nagyszámú mintapont akkor is előállhat, ha a megoldandó probléma sokdimenziós. Ekkor a sokdimenziós bemeneti tér miatt eleve sok tanítópontra van szükség, hogy a feladatot kellően reprezentáló tanítópont-készlet alapján történhessen a háló konstrukciója. (Ezt a sokdimenziós feladatoknál jelentkező nehézséget szokás a dimenzió átkának ( curse of dimensionality ) is nevezni. A kérdéskört általánosabban a 13. fejezetben vizsgáljuk.) Ilyen esetekben a nagy mintapontszám általában nem redundancia következménye, és a középpontok számának csökkentése mindenképpen információvesztéssel jár, a pontokból egy részhalmaz kiválasztása komolyabb megfontolást igényel. A véletlenszerű kiválasztás helyett, a megfelelő pontok kiválasztásánál figyelembe kell vennünk az eredményül kapott háló képességeit is.
A kétféle esetre számos megoldás született. A következőkben előbb egy olyan iteratív eljárást mutatunk be, amely fokozatosan növeli a középpontok számát újabb és újabb tanítópontok középpontként való beiktatásával, amíg megfelelő képességű hálóhoz nem jutunk; majd az egyik legegyszerűbb és az RBF hálózatok középpont-paramétereinek meghatározásánál gyakran alkalmazott klaszterező eljárást, a K- átlagképző vagy K -közép ( K-means ) eljárást ismertetjük röviden.
Az ortogonális legkisebb négyzetes hibájú (OLS) eljárás [Che91] iteratív módon választ középpontokat úgy, hogy közben figyelembe veszi a háló képességét is. Ez azt jelenti, hogy a háló méretét lépésről lépésre növeljük, újabb és újabb bázisfüggvények bekapcsolásával egészen addig, amíg megfelelő teljesítőképességet el nem érünk.
A módszer bemutatásához induljunk ki a háló által megvalósított leképezésből ((5.1’) egyenlet). Ha csak egyetlen bázisfüggvényt alkalmazunk, a szummás kifejezésnek csak egy tagja lesz: a kimenetek egy adott középpontra illesztett bázisfüggvény súlyozott értékeiként adódnak. Hogy az így kapott egy rejtett elemű „háló” milyen képességekkel rendelkezik, azt a rendelkezésre álló ismert válaszú pontokra adott válaszok alapján állapíthatjuk meg. Az egyetlen súly értéke egy olyan túlhatározott lineáris egyenletrendszer megoldásaként nyerhető (ld. (5.5) összefüggés), melynél a G mátrix egyetlen oszlopot és a rendelkezésre álló P tanítópontnak megfelelő P sort tartalmaz. A kapott LS megoldásnak az összes tanítópontra vonatkozó teljesítőképessége alapján dönthető el, hogy az egy rejtett elemű „háló” megfelelően oldja-e meg a feladatot vagy sem.
A megoldás minősége függ az alkalmazott egyetlen bázisfüggvény elhelyezésétől, vagyis a középpont paramétertől. Hogy az egy bázisfüggvénnyel dolgozó hálók közül a legjobbat kapjuk, bázisfüggvény-középpontként az összes tanítópontot végig kell vizsgálni. Amennyiben az egy bázisfüggvényes hálók legjobbika sem elegendően kis hibájú, több bázisfüggvénnyel kell a feladatot megoldani. Így elvben meghatározhatjuk a legjobb két, három, stb. rejtett neuronos RBF hálót. Az eljárás gyakorlati alkalmazása a hatalmas számításigény miatt nem célszerű vagy nem is lehetséges.
Kisebb számításigényű az a változat, amikor a hálót oly módon bővítjük fokozatosan, hogy a már kiválasztott középpontokhoz választunk újabb és újabb középpontokat. Így egy adott komplexitású háló középpontjait már nem módosítjuk. A feladat „mindössze” annyi, hogy a még középpontként fel nem használt pontok közül kell minden lépésben az LS értelemben legjobbat kiválasztani, és a már kiválasztottakhoz új bázisfüggvény-középpontként hozzávenni. A háló méretét most is fokozatosan bővítjük egészen addig, amíg a megfelelő teljesítőképességet el nem érjük. A második változat csak szuboptimumot eredményez, és még mindig elfogadhatatlanul nagy számításigényű. Az OLS eljárás a háló fokozatos bővítését egy ortogonalizáló lépés közbeiktatásával az előbbinél jóval hatékonyabban oldja meg.
Az OLS eljárás bemutatásához induljunk ki a háló leképezésének mátrixos alakjából:
, ( 5 . 7 )
ahol a G mátrix i -edik sora a háló rejtett rétegének válasza az x i bemeneti vektorra , i =1, 2, …, P ; a tanítópontokra adott válaszokból képezett vektor, és w a kimeneti réteg súlyvektora. G tehát felírható, mint egy P sorból álló mátrix:
( 5 . 8 )
Ugyanakkor G az alábbi módon is értelmezhető
( 5 . 9 )
Itt g j az j -edik bázisfüggvénynek a P tanítópontra adott válaszaiból képezett vektor. E szerint a háló válaszaiból képezett vektor
( 5 . 10 )
formában is értelmezhető. Minthogy a kimenetek vektora a g j vektorok súlyozott összegeként állítható elő, ha a g j vektorok lineárisan függetlenek, akkor egyben bázist is alkotnak a kimeneti vektorok terében.
Adott súlyvektor mellett azonban a háló válaszai nem feltétlenül állítják elő hibátlanul a kívánt válaszokat, tehát:
, ( 5 . 11 )
ahol e az egyes tanítópontokban kapott válaszok hibáiból képezett vektor. Gw d -nek a g j bázisvektorok által kifeszített térre való vetületét adja. Minél kevesebb bázisfüggvényt használunk, annál nagyobb hibával tudjuk d -t közelíteni a bázisvektorok által kifeszített térben. A hiba azonban nemcsak attól függ, hogy hány bázisvektort használunk, hanem attól is, hogy melyek ezek a bázisvektorok. A bázisvektorok számát a háló bázisfüggvényeinek száma adja meg, azt pedig, hogy mely bázisvektorokat használjuk, a bázisfüggvények középpont paraméterei határozzák meg. Minél inkább korreláltak a bázisvektorok, annál kisebb hozzájárulást jelentenek a d kimeneti vektor előállításához. Legkedvezőbb az lenne, ha a bázisvektorok ortogonálisak lennének, ekkor ugyanis mindegyik bázisvektor a többitől független hozzájárulást jelentene, ahol az egyes bázisvektorok hozzájárulásának mértéke egyenként számítható. Az OLS eljárás a g j vektorok transzformációja útján egy ortogonális bázisvektor-rendszert hoz létre.
Ennek érdekében dekomponáljuk a G mátrixot az alábbi módon:
. ( 5 . 12 )
Itt A egy olyan M × M -es felső háromszögmátrix, melynek főátlójában csupa egyesek szerepelnek
, ( 5 . 13 )
B pedig egy P × M -es ortogonális mátrix. Az ortogonalitás következménye, hogy B T B = H egy olyan diagonálmátrix, melynek főátlójában a értékek találhatók.
Az ortogonális vektorok által kifeszített tér azonos a g j bázisvektorok által kifeszített térrel, vagyis a kimenetek vektora, d előállítható az ortogonális vektorok súlyozott összegeként is:
, ( 5 . 14 )
ahol a b j ortogonális bázisvektorok súlyait a v vektor komponensei adják. Ennek a súlyvektornak a meghatározása szintén történhet a négyzetes hiba minimalizálásával.
( 5 . 15 )
Itt azonban az ortogonalitás miatt H -1 sokkal egyszerűbben számítható, így a súlyokat egyenként is meg tudjuk határozni.
( 5 . 16 )
Ugyanakkor az is igaz, hogy
, ( 5 . 17 )
vagyis, ha ismerjük A -t és v -t, a keresett w súlyvektor is meghatározható.
Az (5.17) összefüggés származtatásához például a klasszikus a Gram-Schmidt ortogonalizáló eljárással juthatunk el. Alkalmazzuk az eljárást G ortogonalizálására. Az ortogonalizáló eljárás k -adik lépésében olyan b k vektort keresünk, amely a megelőző lépésekben meghatározott k -1 vektor mindegyikére ortogonális. B első vektoraként a g j vektorok bármelyikét választhatjuk. Legyen ezért
( 5 . 18 )
A k -adik vektor ( k =2,…, M ) ezek után a következőképpen nyerhető
, ( 5 . 19 )
ahol
1 ≤ j < k ( 5 . 20 )
Az ortogonalizáló eljárással tehát mind a b j ortogonális bázisvektorok, mind az A mátrix a jk együtthatói meghatározhatók.
Az OLS eljárás célja azonban most nemcsak az, hogy a bázisvektorok mátrixát ortogonalizáljuk, hanem az is, hogy az ortogonális bázisvektorok egy megfelelő részhalmazát kiválasszuk. Addig, amíg a kiindulásnál a G mátrix maximum annyi oszlopból állt, ahány tanítópontunk van (egy bázisfüggvényes hálónál, ha minden tanítópont egyben bázisfüggvény középpont is, a G mátrix egy P × P -s mátrix, ld. (5.3)), most az ortogonális bázisvektorok egy kisebb számú részhalmazát szeretnénk felhasználni. Az eddigi eljárásból az is látszik, hogy az ortogonális bázisvektor-rendszer a kiinduló lépés függvénye, tehát függ attól, hogy b 1 -ként melyik g j bázisvektort választjuk. Sőt, ha nem az összes vektort akarjuk felhasználni, akkor az ortogonális bázisvektorok előállítási sorrendje sem közömbös.
A legfontosabb bázisvektorok kiválasztásához vizsgáljuk meg előbb az egyes bázisvektorok szerepét. Mivel b i és b j ortogonálisak, ha i ≠ j, a kívánt kimenetek négyzetes értéke felírható az alábbi formában:
( 5 . 21 )
Tételezzük föl, hogy a d kívánt válaszok vektora nulla várható értékű (ha ez nem teljesül, akkor vonjuk ki belőle a várható értékét). Ekkor d varianciájának a becslése:
. ( 5 . 22 )
Az (5.22) összefüggés első tagja az a variancia-komponens, ami a bázisvektorokkal kifejezhető, míg a második tagja az ezekkel nem kifejezhető rész. Ebből az is látszik, hogy a kimeneti varianciához a j -edik bázisfüggvény hozzájárulása . Minél nagyobb arányt képvisel ez az érték a kimeneti varianciában, annál fontosabb a b j bázisvektor felhasználása. A j -edik bázisvektornak a kimeneti varianciához való relatív hozzájárulását az
( 5 . 23 )
mennyiség fejezi ki. Ez az arány egy egyszerű és hatékony mértéke lehet az egyes bázisvektorok fontosságának. Ennek felhasználásával relative kis számításigénnyel minden lépésben azt az ortogonális bázisvektort és a megfelelő v j súlyozó együtthatót meg tudjuk meghatározni, melynek a kimeneti varianciához való hozzájárulása a legnagyobb.
Ehhez a Gram-Schmidt eljárást a következő módon alkalmazzuk:
Az első lépésben minden 1 ≤ j ≤ M értékre számítsuk ki a következőket
( 5 . 24 )
Keressük azt az j értéket mely mellett
( 5 . 25 )
és válasszuk ki első bázisvektornak a
( 5 . 26 )
vektort.
A k -adik lépésben, ha k ≥ 2, minden 1 ≤ j ≤ M, j ≠ j 1 , …, j ≠ j k- 1 értékre számítsuk ki a következőket
( 5 . 27 )
Keressük azt a j értéket, mely mellett
, ( 5 . 28 )
és a k -adik bázisvektornak válasszuk a
( 5 . 29 )
vektort, ahol , 1 ≤ i < k .
Az eljárást az M s -edik lépésben állítsuk le, ha
, ( 5 . 30 )
ahol 0 < ρ < 1 egy előre megválasztott küszöbérték.
Az eljárással M s bázisvektort választottunk ki. Bár az OLS eljárás szintén számításigényes, az eredeti középpont-válogató eljárásnál jóval hatékonyabb, hiszen minden egyes új bázisvektor beiktatása az addigi bázisvektorok változatlanul hagyása mellett történik. Az ortogonális bázisvektorok miatt az is igaz, hogy minden újabb bázisvektor a megelőzőktől független hozzájárulást jelent a kimenetek előállításához és ez a hozzájárulás kiszámítható az éppen aktuális háló teljes kiértékelése nélkül. Az aktuális súlyvektor kiszámításához sem kell minden egyes lépésben a pszeudo-inverz számítást elvégezni, hiszen az újonnan kiválasztott bázisvektorok együtthatói egymástól függetlenül számíthatók.
Az eljárás alkalmazásánál fontos a ρ küszöbérték megfelelő megválasztása, mivel ez szabályozza, hogy a végleges háló adott komplexitás mellet milyen pontosságot ér el. Számos alkalmazásban ρ meghatározása maga is az eljárás része. Erre ad egy rendszer-identifikációhoz kapcsolódó példát [Che89].
A standard K -közép ( K-means ) klaszter kialakító algoritmus is feltételezi, hogy az összes tanítópont a rendelkezésünkre áll. A K -means algoritmus célja, hogy K olyan klaszter-középpontot ( , k =1,2,..., K ) határozzon meg, hogy a tanítópontok és a hozzájuk legközelebb eső klaszter-középpont négyzetes távolságainak összege minimális értéket vegyen fel. Tehát, ha X az x i , i =1, 2, ..., P tanítópontok halmazát, pedig azon halmazt jelöli, melynek pontjai a ( k =1,2,..., K ) középponthoz lesznek legközelebb, akkor a következő kifejezés megoldását keressük :
( 5 . 31 )
Az algoritmus az alábbi lépésekből áll:
1. Inicializálás: véletlenszerűen válasszunk meg K középpontot: , k =1,2,..., K.
2. Határozzuk meg minden tanítópontra, hogy mely középponthoz van a legközelebb, vagyis alakítsuk ki a K klasztert. Ha x i -től a legkisebb távolságra lévő középpont , akkor x i a k -adik klaszter, eleme lesz.
3. Határozzuk meg az így kialakított klaszterek új középpontjait. Egy klaszter új középponja legyen a klaszterekbe tartozó mintapontok átlaga: ( 5 . 32 ) ahol az klaszterbe tartozó tanítópontok száma.
4. Fejezzük be az eljárást, ha a mintapontok klaszterbe sorolása már nem változik, illetve adott számú iteráció után.
A középpontok meghatározására további lehetőség az ellenőrzött tanítás alkalmazása. Ebben az esetben a bázisfüggvények paramétereit a kimeneti réteg súlyaihoz hasonló, tanítható paraméterekként kezeljük és például gradiens eljárással tanítjuk. Mivel a bázisfüggvények paraméterei a rejtett réteg leképezését befolyásolják, a kimenti hibát a rejtett, bázisfüggvényes rétegre vissza kell terjeszteni, vagyis itt a hibavisszaterjesztéses algoritmusegy RBF hálóra kidolgozott változatáról van szó.
Ha a pillanatnyi gradiens alapú eljárást alkalmazzuk, meg kell határozni a kimeneti négyzetes hiba adott középpontra vonatkozó parciális deriváltját. Feltételezve, hogy az alábbi általános (vagyis nem skalár σ szélességparaméterrel rendelkező) Gauss bázisfüggvényt alkalmazzuk:
, ( 5 . 33 )
valamint, hogy egykimenetű hálózatunk van, a láncszabályt alkalmazva a derivált a következőre adódik:
( 5 . 34 )
Itt az i -edik bázisfüggvény c i ( k ) szerinti deriváltja az x ( k ) bemenetre adott értéknél, w i pedig az a súly, amivel az i -edik rejtett neuron kimenete szerepel a háló kimentében. A középpont módosító összefüggés ennek megfelelően:
, ( 5 . 35 )
ahol μ a szokásos tanulási tényező. A tanulási tényező értékének megválasztása gyakorlatilag csak tapasztalati úton lehetséges és ez az érték általában más is, mint a kimeneti réteg súlyainak tanításánál alkalmazott LMS eljárás tanulási tényezője. Míg az LMS eljárásnál μ konvergencia-tartományát meg tudjuk határozni, itt ez hasonló módon nem lehetséges. Ennek oka, hogy a kimeneti négyzetes hiba nem kvadratikus függvénye c i -nek, sőt ez a függvénykapcsolat nem is konvex. A nemkonvex hibafelület további következménye, hogy a gradiens alapú eljárás lokális minimumot eredményezhet.
A tanítással meghatározott középpontok természetesen nem fognak egybeesni a bemeneti pontokkal vagy azok részhalmazával. Sokkal inkább úgy igazodnak a tanítópontok elhelyezkedéséhez, mintha egy klaszterező eljárást alkalmaznánk. A középpontok tanítással történő meghatározása a középpontok számának meghatározását nem oldja meg, tehát hasonlóan a K -közép algoritmushoz, ezt a kérdést a tanítástól függetlenül kell megoldani.
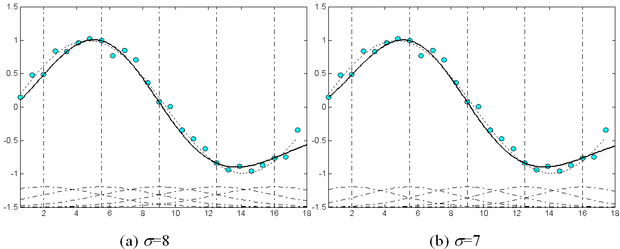
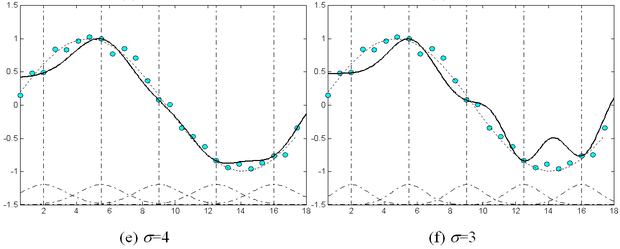
Az RBF hálózatok − extrém értékektől eltekintve − nem érzékenyek a σ k szélességparaméterek megválasztására. Ezt illusztrálja az 5.3 ábra. Az ábrán a szinusz függvény 1 periódusának approximációja látható, különböző szélességparaméter-értékek mellett, zajos mintapontok alapján. Az ábrán a bázisfüggvények száma és elhelyezése mindegyik esetben azonos. Az 5.3 (a) - (f) ábrákon látható eredmények rendre σ =8, 7, 6, 5, 4 és 3 értékkel készültek. Az (e) és (f) beállítások kivételével, ahol σ értéke már túl kicsi, a többi esetben az approximációs tulajdonságok jelentősen nem térnek el egymástól. Az ábra szaggatott vonallal a bázisfüggvényeket is mutatja.
Bár a szélességparaméter viszonylag széles határok között változhat anélkül, hogy az approximációs tulajdonságok lényegesen megváltoznának, a megfelelő σ tartomány, illetve σ érték meghatározására célszerű módszert adni. Egy egyszerű heurisztikus eljárás az R legközelebbi szomszéd módszer ( R-nearest neighbour heuristics ):
, ( 5 . 36 )
ahol az R különböző középpont a középpont R legközelebbi szomszédja.
RBF hálózatoknál gyakori, hogy minden rejtett rétegbeli elemnél azonos σ -t használunk, vagyis σ k = σ, k= 1, ..., K -ra. Tapasztalati eredmények azt mutatják, hogy a közös szélességparaméterre jó becslés, ha egy középpont és a hozzá legközelebbi középpont euklideszi távolságainak az átlagát vesszük:
( 5 . 37 )
ahol a középpont legközelebbi szomszédja. Láthatóan (5.36) és (5.37) között csak az a különbség hogy az előbbi esetben R, az utóbbiban K távolság átlagát vesszük. Az R -heurisztikánál R értéke általában kicsi (2-3), míg K értékét az öszes középpont száma adja meg.
A értékek meghatározása ellenőrzött tanítással is lehetséges. Ekkor − hasonlóan a középpont-értékek tanításához − egy megfelelően származtatott hibavisszaterjesztéses tanításthasználhatunk. Meg kell tehát határoznunk a kimeneti négyzetes pillanatnyi hiba szélességparaméterek szerinti gradiensét. Ha általános esetet tételezünk fel, minden rejtett neuronhoz más szélességparaméter tartozhat, sőt, mivel a bázisfüggvények többdimenziós térben értelmezendők az sem kötelező, hogy a bázisfüggvényekhez skalár értékek tartozzanak. Ekkor a (5.33) szerinti többdimenziós Gauss bázisfüggvénynél az összes dimenzió menti azonos szélességparaméter helyett egy mátrixot tekintve tanító összefüggését kell meghatározni.
, ( 5 . 38 )
ahol
( 5 . 39 )

Ezzel a módosító összefüggés általános alakja:
( 5 . 40 )
A gradiens alapú tanítással meghatározott szélességparaméterekre érvényesek a középpontok ellenőrzött tanításánál említett általános megjegyzések. Tehát itt sem garantálja a tanító eljárás az optimális értékek elérését a lokális minimumok lehetősége miatt. A tanulási tényező megválasztására vonatkozó megállapítás is igaz, vagyis a szélességparaméter tanításánál alkalmazandó μ nagy valószínűséggel különbözni fog mind a kimeneti súlyok, mind a középpontok tanításánál alkalmazott tanulási tényezőktől.
Az RBF hálózatoknak is több változata létezik. John Moody és Christian Darken javasolták a normalizált bázisfüggvények alkalmazását [Moo88]. Gauss függvény esetén ez az alábbi:
. ( 5 . 41 )
A normalizálás itt azt jelenti, hogy bármely bemeneti vektornál ( x ), vagyis az összes rejtett processzáló elem kimenetének (súlyozatlan) összege 1-et ad. A normalizált bázisfüggvények alkalmazását az approximációs tulajdonságok javulását mutató tapasztalatok indokolják [Wer93].
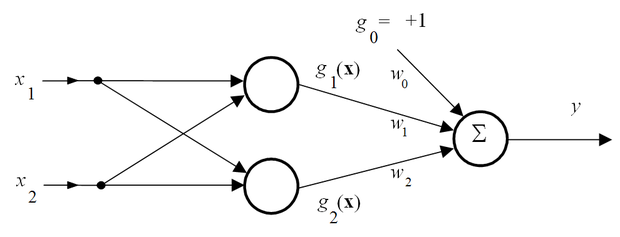
További változatok hozhatók létre attól függően, hogy a kimeneti rétegben alkalmazunk-e eltolás ( bias ) tagot vagy nem. Mind az 5.1, mind az 5.2 ábrán bemutatott hálózat tartalmaz eltolásértéket, amit w 0 biztosít. Ezek az ábrák általános bázisfüggvényes, illetve általános RBF struktúrát mutatnak. Eltolás alkalmazására azonban a bázisfüggvényes hálózatoknál − beleértve az RBF hálózatokat is − nincs mindig szükség. Az RBF hálózatoknak az a változata, amikor minden tanítópont egyben bázisfüggvény középpont is, nem igényli az eltolás alkalmazását. Ezt az RBF háló változatot szokás regularizációs hálónak is nevezni, mert származtatása egy megfelelő regularizációs taggal kiegészített, négyzetes hibát minimalizáló eljárással is lehetséges [Pog90].
Az RBF hálózatok alkalmazásával kapcsolatban részben hasonló nehézségekkel kell szembenéznünk, mint az MLP hálózatok esetében. Itt is gondot jelent a hálózat méretének, vagyis a rejtett rétegbeli processzáló elemek számának ( M ) a meghatározása. Ismereteink szerint jelenleg erre nincs egzakt módszer, értékét tapasztalati megfontolások alapján választhatjuk meg. Ugyanakkor meg kell jegyezni, hogy az előbbiekben bemutatott OLS eljárás valójában a háló komplexitási problémára adható egy lehetséges válasz.
Hasonlóan, a szélességparaméternél R értékének megállapítására is csak tapasztalati eljárások állnak rendelkezésünkre. Ezen módszerek lényegében különböző értékű M és R paraméterek mellett felépített hálózatok tanítását és tesztelését végzik, és a megtanított hálózatok képességeiből próbálnak a megfelelő hálózat-méretre következtetni, így tulajdonképpen a kereszt kiértékelés valamilyen változatának tekinthetők. A kereszt kiértékelési eljárásnak a tanítópontok számától függő valamelyik változata tehát alapvető fontosságú szerepet tölt be a hálók konstrukciójánál.
A rejtett neuronok számának meghatározásakor figyelembe kell venni az RBF (és általában a bázisfüggvényes hálózatok) egy specialitását. E hálózatok többsége − szemben az MLP-vel − lokális approximációtvégez, ami azt jelenti, hogy egy bázisfüggvénynek a középpont egy véges környezetében van csak számottevő hatása. E véges környezet mérete függ a bázisfüggvénytől és a függvény σ szélességparaméterétől. Minél kisebb σ értéke, annál kisebb tartományba eső bemenet esetén lesz az adott bázisfüggvénynek (az adott rejtett rétegbeli neuronnak) jelentős hozzájárulása a kimenethez. Azt a tartományt, amelybe eső bemenetekre a bázisfüggvény jelentős értéket ad a bázisfüggvény érzékelési mezőjének ( receptive field ) szokás nevezni. Az RBF hálózatoknál az érzékelési mező a legtöbb esetben gyakorlatilag véges, még végtelen tartójú pl. Gauss bázisfüggvényeknél is.
A bázisfüggvények számát a szélességparaméter, de leginkább az approximálandó függvény Fourier transzformált tartománybeli tulajdonságai határozzák meg. Ha a tanítópontok egyben középpontok is, az RBF háló valójában a tanítópontok között végez interpolációt úgy, hogy a tanítópontokban a megtanulandó függvényt pontosan előállítja. A tanítópontokat ebben az esetben, mint mintavételi értékeket is értelmezhetjük, így az RBF hálózatos függvény-approximáció egy mintavételi értékekből történő (általában többdimenziós) jelvisszaállítási feladatként is felfogható. A megfelelő jelvisszaállítás − amennyiben a függvény Fourier tartománybeli viselkedését ismerjük − megszabja a mintavételezés sűrűségét, a mintavételi pontok számát, ami itt egyben a tanítópontok számát és a rejtett neuronok számát is jelenti. A gyakorlatban a mintavételezés Nyquist elmélete alapján történő rejtett réteg konstrukció általában nem lehetséges, hiszen az approximálandó függvény jellemzőit nem ismerjük. Ráadásul gyakorlati feladatoknál a rendelkezésünkre álló tanítópontok (a mintavételi pontok) a függvény értelmezési tartományának számunkra fontos részén belül szinte sohasem helyezkednek el egyenletesen, ezért a probléma a nemegyenletes (többdimenziós) mintavételezéssel, a nemegyenletesen elhelyezkedő mintavételi pontokból történő jelvisszaállítással [Kim90] hozható kapcsolatba.
Ha a tanítópontoknál kevesebb a rejtett rétegbeli neuronok száma, tehát amikor pl. klaszterezéssel határozzuk meg a középpont paramétereket, a helyzet még nehezebb, hiszen itt a középpontok mintavételi pontokként nem is értelmezhetők. A mintavételi értékekből való jelvisszaállítással való kapcsolat azonban arra felhívja a figyelmet, hogy a tanítópontok száma és elhelyezkedése, az approximálandó függvény Fourier tartománybeli viselkedése, a bázisfüggvények megválasztása és a rejtett neuronok száma nem függetlenek egymástól.
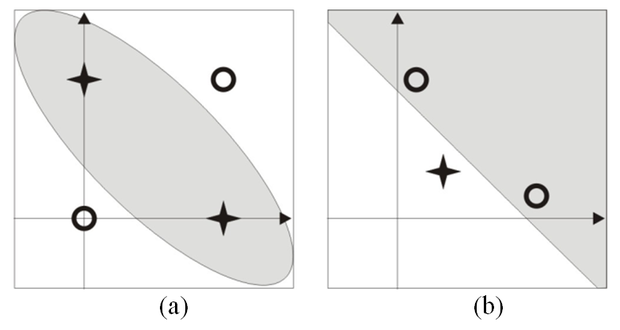
Láttuk, hogy az RBF háló interpretálható úgy is, mint egy olyan perceptron, ahol a bemenetek nem közvetlenül, hanem egy nemlineáris transzformációt követően kerülnek a perceptron bemeneteire. A nemlineáris transzformáció – a perceptron kapacitásáravonatkozó Cover tétel alapján [Cov65] – általában dimenziónövelő transzformáció is egyben. Számos esetben azonban a nemlineáris transzformáció dimenziónövelés nélkül is biztosíthatja a lineáris szeparálhatóságot. Erre mutatunk példát a kizáró VAGY (XOR) kapcsolat RBF hálóval történő megoldásával.
Konstruáljunk egy olyan RBF hálót, melynek két rejtett neuronja van, tehát két bázisfüggvényt alkalmazzunk (5.4 ábra).
A Gauss bázisfüggvények legyenek az alábbiak
( 5 . 42 )
ahol a c 1 és c 2 középpontvektorok
, . ( 5 . 43 )
Az (5.42) összefüggés olyan Gauss bázisfüggvényt definiál, ahol 2 σ 2 =1. Az ábrán látható RBF háló a XOR probléma négy mintapontja közül kettőt használ középpontnak. A hálónak három szabad paramétere van: a w 0 eltolásérték, valamint w 1 és w 2 . A súlyok analitikusan is meghatározhatók. Mivel négy tanítópontunk van, ehhez egy túlhatározott lineáris egyenletrendszert kell megoldanunk, ami a pszeudo-inverz meghatározásával lehetséges.
( 5 . 44 )
A rejtett réteg válaszaiból képezett G mátrix a fenti bázisfüggvények mellett a következőre adódik:
( 5 . 45 )
A kívánt válaszok vektora a XOR problémának megfelelően
( 5 . 46 )
Elvégezve a pszeudo-inverz számítást a megoldásvektor a következőre adódik:
( 5 . 47 )
Az 5.5 (a) ábra a bemeneti térben, a (b) ábra a transzformált térben mutatja a mintapontokat. Látható, hogy a transzformált térben a pontok már lineárisan szeparálhatók. Ugyanakkor az is látható, hogy a szeparáló egyenes nem megy át az origón, ami azt jelenti, hogy szükség van eltolás tagra, amint ezt a megoldás mutatja is.