3.2. Az adaline

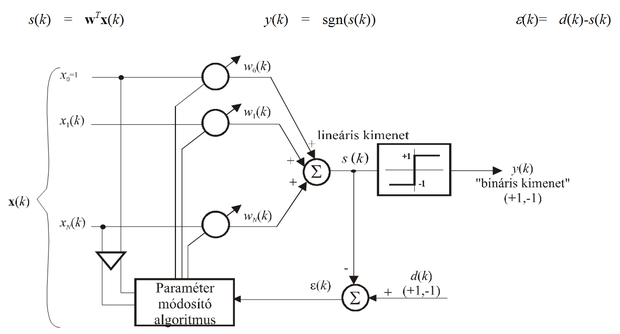
A küszöbfüggvényt alkalmazó perceptronon kívül az előbbi hálózat különböző változatai is elterjedtek. Ezen változatokban a különbség a kimeneti hiba értelmezésében, illetve a kimeneti nemlinearitásban és ebből következően a tanulási eljárásban van. A perceptronnal lényegében megegyező felépítésű hálózat az adaline, amely csaknem egyidős a perceptronnal és amelyet Bernard Widrow és munkatársai javasoltak [Wid60]. A két hálózat közötti alapvető különbség a hiba értelmezésében és a háló tanításában van. Míg a Rosenblatt-féle perceptronnál a hálózat tényleges kimenetét hasonlítjuk össze a kívánt válasszal, addig az adaline-nál a lineáris kombináció eredményét, tehát egy lineáris hálózatrész kimenetét vetjük össze egy kívánt jellel (ld. 3.4 ábra). (A hálózat elnevezése is ezt tükrözi: adaline = adaptive linear element, vagy adaptive linear neuron.) A hálózat tényleges kimenete azonban itt is egy küszöbfüggvény nemlinearitás után kapható.

3.2.1. Az adaline tanítása

Mivel a hiba szempontjából a lineáris kimenetet tekintjük az adaline kimenetének, a kimenet a paraméterek lineáris függvénye és négyzetes hiba estén a kritériumfüggvény kvadratikus felületet jelent. Az adaline tanításánál tehát alkalmazhatók a 2.5.1. alfejezetben bemutatott eljárások. Az adaline súlyvektorának optimális értékét tehát akár analitikusan, a Wiener-Hopf egyenlet alapján, akár gradiens alapú iteratív eljárással meghatározhatjuk. Az iteratív gradiens alapú eljárások közül is leggyakrabban az LMS algoritmust alkalmazzuk, annak nagyfokú egyszerűsége miatt.

3.4. ábra - Az adaline felépítése a hibaképzéssel és a paramétermódosítással
Az adaline felépítése a hibaképzéssel és a paramétermódosítással

A Wiener-Hopf egyenlet a négyzetes hiba várható értékének minimumához tartozó paraméter-vektort eredményezte, az LMS algoritmusról pedig láttuk, hogy olyan iteratív eljárás, amely mindig a pillanatnyi négyzetes hiba csökkentésének irányában módosítja az aktuális paramétervektort. Azt is láttuk, hogy a hiba várható értékét csak becsülni tudjuk, mivel a mintapontok eloszlását általában nem ismerjük. A mintapontok eloszlásának ismerete nélkül kritériumfüggvénynek a mintapontokban meghatározható négyzetes hiba átlagát vagy összegét tekinthetjük:

C(w)= 1 P ∑ i=1 P ( d i −f(w, x i ) ) 2 MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqkLspw0le9v8qqaqFD0xXdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGdbGaaeikaiaahEhacaqGPaGaeyypa0ZaaSaaaeaacaqGXaaabaGaamiuaaaadaaeWbqaamaabmaabaGaamizamaaBaaaleaacaWGPbaabeaakiabgkHiTiaadAgacaqGOaGaaC4DaiaacYcacaWH4bWaaSbaaSqaaiaadMgaaeqaaOGaaeykaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaeaacaWGPbGaeyypa0JaaGymaaqaaiaadcfaa0GaeyyeIuoaaaa@4FA8@ (3.15)

Adaline-nál a lineáris kapcsolat miatt f(w,x)= w T x  MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaiaabIcacaWH3bGaaiilaiaahIhacaqGPaGaeyypa0JaaC4DamaaCaaaleqabaGaamivaaaakiaahIhacaaMc8oaaa@4069@ . Az átlagos négyzetes hiba ilyenkor felírható az alábbi mátrixos formában is:

C(w)= (d−Xw) T (d−Xw) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqkLspw0le9v8qqaqFD0xXdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGdbGaaeikaiaahEhacaqGPaGaeyypa0JaaeikaiaahsgacqGHsislcaWHybGaaC4DaiaabMcadaahaaWcbeqaaiaadsfaaaGccaqGOaGaaCizaiabgkHiTiaahIfacaWH3bGaaeykaaaa@4805@ (3.16)

ahol d a tanítópontokbeli kívánt válaszokból képezett P elemű oszlopvektor, X a bemeneti vektorokból képezett mátrix

X=[ x 1 T x 2 T ⋮ x P T ] MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqkLspw0le9v8qqaqFD0xXdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWHybGaeyypa0ZaamWaaeaafaqabeabbaaaaeaacaWH4bWaa0baaSqaaiaaigdaaeaacaWGubaaaaGcbaGaaCiEamaaDaaaleaacaaIYaaabaGaamivaaaaaOqaaiabl6UinbqaaiaahIhadaqhaaWcbaGaamiuaaqaaiaadsfaaaaaaaGccaGLBbGaayzxaaaaaa@4703@ , (3.17)

w pedig a keresett paramétervektor. A megoldásvektor ideális esetben azt biztosítja, hogy

d=Xw MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqkLspw0le9v8qqaqFD0xXdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWHKbGaeyypa0JaaCiwaiaahEhaaaa@3C80@ , (3.18)

vagyis egy lineáris egyenletrendszert kapunk. A lineáris egyenletrendszer megoldása

w= X −1 d MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqkLspw0le9v8qqaqFD0xXdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWH3bGaeyypa0JaaCiwamaaCaaaleqabaGaeyOeI0IaaGymaaaakiaahsgaaaa@3E5F@ , (3.19)

amennyiben X inverze létezik. X-1 létezésének szükséges feltétele, hogy X kvadratikus mátrix legyen. (3.17) alapján látható, hogy X P sorból és N+1 oszlopból áll. A sorok száma az egyenletek számát, az oszlopok száma az ismeretlenek számát adja meg. Inverz csak akkor létezhet, ha P=N+1, sőt még így is csak akkor, ha X rangja teljes, vagyis N+1. Ez akkor áll elő, ha pont annyi tanítópontunk van, mint ahány ismeretlen súly található a hálózatban továbbá, ha a bemeneti vektorok lineárisan függetlenek egymástól. Ha az inverz nem létezik, a pszeudo- vagy Moore-Penrose inverz alkalmazható, amikor is a megoldásvektort az alábbi formában kapjuk:

w ∗ = X † d= ( X T X ) −1 X T d MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaC4DamaaCaaaleqabaGaey4fIOcaaOGaeyypa0JaaCiwamaaCaaaleqabaGaaCiiGaaakiaahsgacqGH9aqpdaqadaqaaiaahIfadaahaaWcbeqaaiaadsfaaaGccaWHybaacaGLOaGaayzkaaWaaWbaaSqabeaacqGHsislcaaIXaaaaOGaaCiwamaaCaaaleqabaGaamivaaaakiaahsgaaaa@45EC@ (3.20)

Vegyük észre, hogy ugyanerre a megoldásra jutunk, ha a (3.16) összefüggés gradiensének nulla értékét biztosító paramétervektort határozzuk meg:

∂C(w) ∂w =−2 X T d+2 X T Xw=0 MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqkLspw0le9v8qqaqFD0xXdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWcaaqaaiabgkGi2kaadoeacaqGOaGaaC4DaiaabMcaaeaacqGHciITcaWH3baaaiabg2da9iabgkHiTiaaikdacaWHybWaaWbaaSqabeaacaWGubaaaOGaaCizaiabgUcaRiaaikdacaWHybWaaWbaaSqabeaacaWGubaaaOGaaCiwaiaahEhacqGH9aqpcaWHWaaaaa@4C63@ . (3.21)

Ugyanis ekkor eredményként a normál egyenletnek nevezett összefüggést kapjuk:

X T Xw= X T d MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqkLspw0le9v8qqaqFD0xXdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWHybWaaWbaaSqabeaacaWGubaaaOGaaCiwaiaahEhacqGH9aqpcaWHybWaaWbaaSqabeaacaWGubaaaOGaaCizaaaa@4062@ , (3.22)

melyből a megoldásvektor a keresett paraméter LS becslése, amely megegyezik (3.20)-szal:

w ∗ = ( X T X ) −1 X T d MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqkLspw0le9v8qqaqFD0xXdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWH3bWaaWbaaSqabeaacqGHxiIkaaGccqGH9aqpdaqadaqaaiaahIfadaahaaWcbeqaaiaadsfaaaGccaWHybaacaGLOaGaayzkaaWaaWbaaSqabeaacqGHsislcaaIXaaaaOGaaCiwamaaCaaaleqabaGaamivaaaakiaahsgaaaa@44F0@ (3.23)

Vegyük észre azt is, hogy a (3.23) összefüggés megfeleltehető a Wiener-Hopf egyenletnek, mivel XTX az R=E{xxT} autokorrelációs mátrix, Xd pedig a p=E{xd} keresztkorrelációs vektor becslésének tekinthető.

A két elemi neuron összehasonlításánál meg kell állapítanunk, hogy a felépítésük azonossága mellett több szempontból is jelentős különbségeket mutatnak. A perceptron és az adaline tanítása alapvetően eltérő még akkor is, ha a perceptron tanulás (3.2) összefüggéssel megadott iteratív eljárása formailag megegyezik az LMS algoritmussal. A perceptron tanulás egy hibakorrekciós eljárás, ahol − lineárisan szeparálható mintapontok esetén − a konvergencia bármely α > 0 mellett biztosított, míg az LMS algoritmus egy pillanatnyi gradiensen alapuló gradiens eljárás. Ennek konvergenciáját már szigorúbb feltétel biztosítja, hiszen itt a tanulási tényezőre a (2.69) összefüggésben megadott felső korlátnak is érvényesnek kell lennie.

A hiba értelmezésénél, illetve a tanításnál lévő különbségek mellett a számítási képességet tekintve is különbözik az adaline a Rosenblatt perceptrontól. Az adaline bármely feladat megoldásánál használható, és minden esetben megoldást ad. Tehát nem kell kikötnünk, hogy a megoldandó feladat lineárisan szeparálható legyen. Ugyanakkor azt is látni kell, hogy egy általános feladatnál semmi biztosítékunk nincs arra, hogy a mintapontok által képviselt leképezést az adaline hibátlanul meg tudja tanulni. A tanuló eljárás mindössze annyit garantál, hogy megoldásként a kvadratikus hibafelület minimumpontjához tartozó paramétervektort kapjuk. Ebből azonban még nem következik, hogy az optimumnál a négyzetes (átlagos négyzetes) hiba nulla is lesz.