A Rosenblatt perceptron vagy egyszerű perceptron egy olyan hálózat, amely képes arra, hogy – megfelelő beállítás, tanítás után – két lineárisan szeparálható bemeneti mintahalmazt szétválasszon. A lineáris szeparálhatóság azt jelenti, hogy a bemeneti mintateret egy síkkal (hipersíkkal) két diszjunkt tartományra tudjuk bontani úgy, hogy a két tartomány eltérő osztályba tartozó bemeneti mintapontokat tartalmazzon. Az egyszerű perceptron tehát kétosztályos esetekben lineáris osztályozási feladatok ellátására alkalmas. A későbbiekben az egyszerű perceptront továbbfejlesztették több-elemű, ill. többrétegű hálózatokká (multilayer perceptron, MLP), amelyek képességei az egyszerű perceptron képességeit messze felülmúlják.
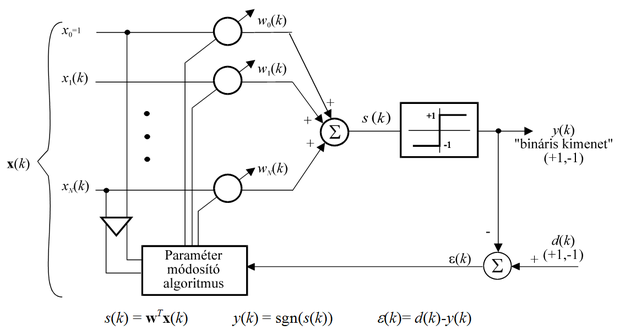
Az egyszerű perceptron felépítéséből (3.1 ábra) látható, hogy ez egy lineáris kombinációt megvalósító hálózat, amelynek a kimenetén egy küszöbfüggvény-nemlinearitás szerepel, vagyis valójában egyetlen memória nélküli processzáló elem.
A küszöbfüggvény a lineáris kombináció eredményeként kapott súlyozott összeg (s) előjelét szolgáltatja kimeneti jelként.
, (3.2)
ahol sgn(.) az előjelfüggvény (szignum függvény).
A perceptron bemenetére az x (N+1)-dimenziós vektor kerül, ahol az x1, … , xN bemeneti komponensek jelentik a tényleges bemenőjelet, x0 pedig az ún. eltolás (bias) értéket. A bias szerepe azt biztosítani, hogy a kimenet előjelváltása ne feltétlenül a nulla bemeneti vektornál, hanem a kívánt leképezésnek megfelelő bemeneteknél történjen. A tényleges bemenet dimenziója tehát N, az eltolásérték figyelembevételével kapott x dimenziója pedig N+1.
A tanítás során a megfelelő elválasztó felület meghatározása a cél, vagyis azon w súlyvektor meghatározása, kialakítása, amely mellett az egyik osztálybeli bemeneti adatokra a lineáris kombináció eredménye pozitív, míg a másik osztálybeli pontokra negatív. Az elválasztó felületet azon bemeneti pontok határozzák meg, ahol
. Az elválasztó felület a bemeneti mintatérben tehát egy, az origón átmenő, a súlyvektorra (w) merőleges sík (hipersík).
Felmerül a kérdés, hogy mi történik, ha a bemeneti mintapontok nem választhatók szét lineáris felülettel. Ebben az esetben nyilvánvaló, hogy semmilyen tanító eljárással sem kaphatunk olyan hálózatot, amely az osztályozási feladatot tökéletesen megoldja. Ilyenkor a feladat lineárisan nem szeparálható, s így a perceptron az ilyen feladatok megoldására alkalmatlan. Természetesen elképzelhető egy olyan megoldás is, amelynél az elválasztó hipersík a mintapontok többségét helyesen választja szét, de − a bemeneti adatok elhelyezkedésétől függően − lesznek olyan mintapontok, melyekre a hálózat rossz választ ad. Ebben az esetben nyilván az a célunk, hogy a hibásan osztályozott adatok számát minimalizáljuk.
A továbbiakban a hálózat működését úgy vizsgáljuk, hogy a bemenetről feltételezzük a lineáris szeparálhatóságot. E feltételezés mellett megmutatjuk, hogy a perceptron a lineáris szeparáló felületet véges számú tanuló lépés alatt megtalálja.
3.1.1. A perceptron tanulása
Vezessük be a következő jelöléseket. Jelölje
azon bemeneti mintapontok halmazát, amelyek az (1) osztályba,
pedig azon bemeneti mintapontok halmazát, amelynek elemei a (2) osztályba tartoznak, és tételezzük fel, hogy mind
, mind
véges számú vektort tartalmaz. Jelöljön továbbá
egy olyan súlyvektort, amely mellett a hálózat jól osztályoz, vagyis
>0, ha
és
<0, ha
.
A hálózat tanítását a következőképpen végezzük: egyenként vegyük sorra az összes bemeneti mintapontot, határozzuk meg mindegyik lépésben a hálózat válaszát, és az alábbi összefüggés szerint módosítsuk a súlyvektort:
(3.3)
A súlymódosítás (3.3) összefüggése formailag megegyezik az előző fejezetben bemutatott LMS algoritmussal, ha az itt szereplő α-t megfeleltetjük az LMS algoritmus μ tanulási tényezőjének. Az egyezés azonban csak formai, ahogy ez a következőkből kiderül. Amennyiben mind d(k), mind y(k) csak két értéket (±1 vagy 0 és 1) vehet fel, és α értékét 1-re választjuk, hibás válasz esetén ε(k) abszolút értéke is csak két lehetséges konstans érték (2, ill. 1) egyike lehet, míg a hiba előjele a tényleges értékektől függően változik; vagyis valójában a pillanatnyi bemenőjel konstans-szorosával történik a súlykorrekció:
, (3.4)
ahol α(k) értéke ±2, ill. ±1 lehet.
A súlymódosítás ez utóbbi formája mutatja, hogy a formai hasonlóság ellenére itt valóban nem az LMS algoritmussal van dolgunk, vagyis a súlymódosítás nem egy hibafelület negatív gradiensének irányában történik, hanem a súlyvektort egyszerűen a helytelenül osztályozott bemenővektorral arányosan módosítjuk. Ez a módosítás szemléletesen azt jelenti, hogy a súlyvektort a hibásan osztályozott bemeneti vektor irányában (vagy azzal ellentétes irányban) elforgatjuk, s így a módosítás után a skalár szorzat a kívánt értékhez közelít.
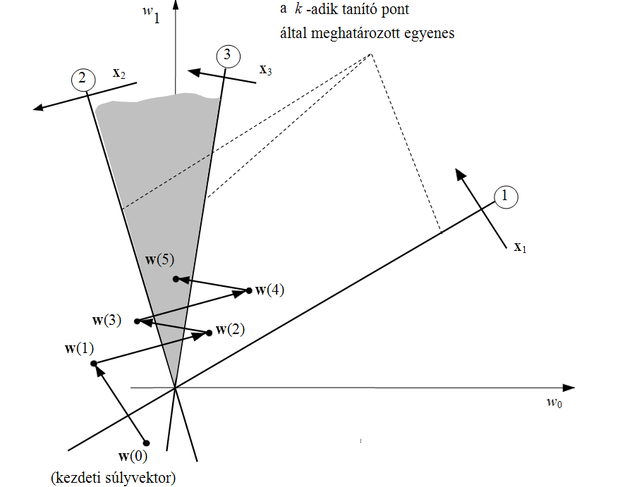
A tanító lépés során a súlyvektort olyan módon változtatjuk, hogy a módosított súlyvektorral a hálózat válasza a helyes értékhez közelítsen. A tanítás hatását a súlyvektorok terében a 3.2 ábrán követhetjük nyomon. A súlyvektorok terében minden bemenővektor egy hipersíkot (kétdimenziós súlytérben egy egyenest) határoz meg. Az egyenes pontjai egyben azon súlyvektorokat is megadják, amelyek mellett a bemenővektor és a súlyvektor skalár szorzata zérus, vagyis az egyenes merőleges a bemeneti mintavektorra. (Másképp fogalmazva a mintavektort a súlytérben olyan hipersíkkal reprezentáljuk, amelynek normálvektora épp a mintavektor.) A hipersík (egyenes) negatív oldalán elhelyezkedő súlyvektorok esetén a hálózat kimenete -1 lesz, míg ha a súlyvektor az egyenes pozitív oldalán található, akkor a hálózat válasza +1.
Súlymódosításra akkor van szükség, ha az aktuális súlyvektor egy tanítópont által meghatározott hipersíknak (egyenesnek) nem a tanítópont osztályának megfelelő oldalán helyezkedik el, vagyis a skalár szorzat nem megfelelő előjelű. Ilyenkor a súlyvektort olyan módon változtatjuk, hogy a skalár szorzat a módosított súlyvektorral megfelelő előjelű legyen − a súlyvektor a hipersík megfelelő oldalára kerüljön −, vagy legalábbis a súlyvektort a helyes irányba mozdítsuk.
Az ábra azt a feltételezett esetet mutatja, amikor három tanítópontunk van, amelyek közül x1 és x3
elemei, míg x2
eleme, vagyis
> 0, ha i=1 és 3, ill.
< 0, ha i=2. A
megoldásvektornak tehát a súlytérben az x1 és x3 tanító pontokat reprezentáló egyenesek (1 és 3) pozitív oldalán, míg az x2-t reprezentáló egyenes (2) negatív oldalán kell elhelyezkednie. Ezeket a feltételeket a súlytérben árnyékoltan jelölt területet pontjai elégíti ki, tehát a megoldásvektornak ezen területen belül kell lennie.
A súlyvektor lépésenkénti módosítását az ábrán követhetjük. x2 esetében pl. módosításra van szükség, hiszen
> 0, holott
, tehát negatív eredményt kellett volna kapnunk. A súlyvektor értékét x2-vel arányosan csökkentenünk kell. E módosítás következtében létrejött w(2) súlyvektor viszont rosszul osztályozza x3-at, tehát ismételt módosításra van szükség, ezúttal a súlyvektorhoz egy, az x3-mal arányos vektort kell hozzáadnunk. Az eljárást így kell folytatnunk mindaddig, míg az összes tanító vektorral megfelelő előjelű skalár szorzatot nem kapunk, vagyis, amíg a megoldás-tartományon belülre nem kerül a súlyvektor. Az ábrán ez w(5)-nél következik be.
A továbbiakban megmutatjuk, hogy a perceptron a lineáris szeparáló felületet véges számú tanuló lépés alatt megtalálja.
A bizonyítás azon alapul, hogy
növekedése két korlát közé szorítható: egyrészt
<
kM, másrészt
, ahol M a bemeneti mintavektorok normanégyzetének felső korlátja:
, b pedig a megoldás-súlyvektorra vonatkozó
ha
és
ha
feltételek kis pozitív konstansa.
3.1.2. A perceptron tanulás konvergenciája
Az egyszerűbb tárgyalás kedvéért a kiinduló tanítópontokból alakítsunk ki egy módosított mintahalmazt,
-ot, ami az
-beli pontokból és az
-beli pontok mínusz egyszereséből áll. Ez azt jelenti, hogy
-ra
> 0 kell teljesüljön, vagyis a módosított tanítóhalmaz min-den elemére igaz, hogy a megoldás súlyvektor által meghatározott sík pozitív felén fog elhelyez-kedni.
Tanító lépésre akkor van szükség, ha a pillanatnyi súlyvektor a bemenetre kerülő mintavektort nem megfelelő osztályba sorolja, vagyis, ha bármely
-ra a pillanatnyi súlyvektorral végzett skalár szorzat
. A módosított mintahalmazzal végzett tanítás esetén
, (3.5)
ahol x(k) tehát a k-adik tanító lépésben a perceptronra kerülő olyan minta, amit az aktuális súlyvektor mellett a perceptron rosszul osztályoz. Minden korrekciós lépésben a pillanatnyi (módosított) bemenővektor konstansszorosát adjuk a súlyvektorhoz, ahol most már α > 0.
A módosított tanító pontok felhasználása során képezzünk egy képzeletbeli listát, amelybe csak azok a tanító pontok tartoznak, amelyeket az adott lépésben a hálózat hibásan osztályoz. Ez azt jelenti, hogy ha w(k-1) jelöli a k-adik lépésben az aktuális súlyvektort és x(k) a képzeletbeli listának azt az elemét, amit a k-adik lépésben veszünk elő, akkor
adódik, tehát súlymódosításra van szükség. A tanítás során a listában az eredeti mintahalmaz minden eleme akárhányszor előfordulhat.
Kövessük végig a súlyvektor alakulását feltételezve, hogy a kiinduló érték
. Az első, a második, ill. a k-adik lépésben kialakuló súlyvektor ennek megfelelően:
(3.6)
Képezzük a
skalár szorzatot:
, (3.7)
Felhasználva a Schwartz egyenlőtlenséget
(3.8)
amiből adódik, hogy:
(3.9)
vagyis, a súlyvektor normanégyzete legalább a lépésszám négyzetével arányosan nő.
A súlyvektor normanégyzetére ugyanakkor felső korlát is állítható, ugyanis
, (3.10)
így felírható, hogy
. (3.11)
Mivel tanító lépésre azért van szükség, mert
, ebből következik, hogy
. (3.12)
Amennyiben a kezdeti súlyvektor hossza nulla, vagyis
, a fentiekből adódik, hogy
, (3.13)
feltéve, hogy kiinduló megállapításunk, miszerint az összes tanító vektor normanégyzete felülről korlátos, igaz. Ez azt jelenti, hogy a vektor normanégyzete nem nőhet a lépésszámmal arányosnál gyorsabban. A két korlát összevetéséből következik, hogy véges számú lépés után az eljárásnak le kell állnia.
A tanító lépések számának felső korlátja,
arányos a bemeneti vektor dimenziójával, de nem függ a tanítópontok számától. Természetesen egy tényleges tanító eljárásnál a konvergencia ideje függ a tanítópontok számától, hiszen minél több tanítópontunk van, annál több pontra kell elvégezni az ellenőrzést, hogy vajon a pillanatnyi súlyvektor mellett a hálózat már helyesen működik-e. Azt is látnunk kell, hogy a konvergencia ténye nem függ α értékétől, hiszen csupán annyit kötöttünk ki, hogy legyen α > 0. A konvergencia sebességét azonban már befolyásolja α megválasztása. Így a perceptron tanulásnak különböző változatai alakultak ki, melyek α megválasztásában térnek el. Az eddig bemutatott tanulásnál α előre rögzített konstans, ezért ezt szokás fix növekményes tanulási szabálynak is nevezni, szemben a lépésenként változó α-t használó módszerekkel. Minthogy elvi különbség ezen módszerek között nincs, a változó növekményes eljárásokat nem részletezzük. A különböző perceptron tanulási változatok részletes bemutatása megtalálható pl. a következő irodalmakban: [Nil65], [Has95], [Vee95].
3.1.3. A perceptron kapacitása
Mint a neurális hálózatok többsége, a perceptron is felfogható, mint egy asszociatív memória. A hálózatnak bizonyos bemenetekre kell jó válaszokat adnia, asszociálnia, amelyet úgy érünk el, hogy a hálózat súlyainak meghatározásához tanítópontokat használunk fel. Valójában tehát a tanítópontok felhasználása úgy is felfogható, mint egy tárolási folyamat, ahol a tanítópontokat valamilyen módon a hálózat súlyaiban tároljuk. Felmerül a kérdés, hogy hány tanítópont tárolható a hálózatban úgy, hogy a háló a megkívánt működést mutassa, illetve általában milyen válaszokat ad a hálózat egy megtanított esetben. Erre a kérdésre ad feleletet a hálózatok kapacitása. Az alábbiakban a perceptron kapacitásátvizsgáljuk [Cov65].
A perceptront eddig úgy mutattuk be, mint egy olyan egyszerű hálózatot, amely az N-dimenziós mintateret egy (N-1)-dimenziós hipersíkkal két tartományra tudja bontani. A perceptron szeparáló képességével kapcsolatban a következő kérdés merül fel: hány, két különböző osztályból származó pontot helyezhetünk el véletlenszerűen egy N-dimenziós mintatérben akkor, ha azt kívánjuk, hogy a két osztály pontjai egy hipersíkkal szétválaszthatók legyenek. Másképp fogalmazva: N-dimenziós bemeneti pontok esetén, P véletlenszerűen kiválasztott pont mellett
kétosztályos szeparálás − vagyis amikor a pontok egy részéhez +1-et, a többihez -1-et rendelünk − lehetséges; kérdés, hogy a
lehetőség közül hány olyan eset van, amikor a két osztályba tartozó pontok elválasztása hipersíkkal megtörténhet, tehát amikor a szeparálási feladatot egy perceptron meg tudja oldani.
Jelöljük ezen esetek számát L(P,N)-nel. Definiáljuk a perceptron kapacitását úgy, mint a lineárisan szeparálható kétosztályos esetek számának és az összes kétosztályos eset számának arányát, vagyis C(P,N)=L(P,N)/
. Megmutatható, hogy a kapacitás a következő összefüggéssel adható meg:
(3.14)
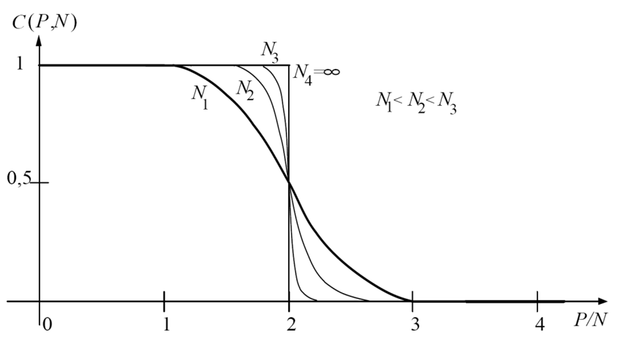
A kapacitás meghatározásának részletes bemutatásától eltekintünk (az érdeklődő olvasó a részletes származtatást például a [Her91] irodalomban megtalálja). A kapacitás alakulását a P/(N+1) arány függvényében a 3.3 ábrán mutatjuk be.
Látható, hogy ha N elég nagy, akkor P<2N esetében gyakorlatilag az összes kétosztályos szeparálás lineáris szeparálás, míg ezen érték fölött lineáris szeparálás egyre kevésbé lehetséges: ha P/N>>2 a lineárisan szeparálható esetek száma nullához tart. Az is látható, hogy, ha
, akkor C(P, N)=1, vagyis, ha a mintapontok száma nem nagyobb, mint a bemeneti tér dimenziója és a pontok általános elhelyezkedésűek, a lineáris szeparálás mindig lehetséges, bármilyen módon is rendeljük a pontokat a két osztályhoz. A pontok akkor és csak akkor általános elhelyezkedésűek, ha (*) P>N és a P pontból nem tudunk kiválasztani N+1 olyan pontot, melyek egy (N-1)-dimenziós hipersíkon helyezkednek el; illetve, ha (**) P≤N és a P pont nem helyezkedik el egy N-2 dimenziós hipersíkon.
A perceptron kapacitásra vonatkozó eredmény alapján látható, hogy ha a tanítópontok száma a pontok dimenziójához képest elegendően nagy, akkor a mintapontok lineárisan nem lesznek szeparálhatók. A gyakorlati problémák döntő többsége lineárisan nem szeparálható feladat, vagyis az egyszerű perceptronnal nem megoldható.
A perceptron kapacitásmeghatározásának a jelentősége az, hogy ezáltal megmutatható, hogy a bemeneti szeparálandó pontok számához viszonyítva kellően nagyra választva a bemeneti tér dimenzióját − ami azt is jelenti egyben, hogy kellően nagyra választva a perceptron súlyainak számát − a kétosztályos feladatok lineárisan szeparálható feladatok lesznek. Ezt az eredményt bizonyos hálózatok konstrukciójánál fel is használhatjuk (ld. pl. a bázisfüggvényes hálózatokat, melyeket a 6. fejezet mutat be).