Amikor neuronhálók tanulásáról beszélünk a tanulás egyik legalapvetőbb, elemi formájáról van szó. Mérési adatokból, megfigyelésekből kell egy megfigyelt rendszerről, jelenségről, folyamatról általános ismereteket nyerni. Láttuk, hogy a tanuló eljárás értelmezhető úgy is, mint egy, a mintapontokkal jellemzett rendszer egyfajta modelljének a létrehozása. A rendszerről egy olyan modellt szeretnénk megalkotni, melynek bemenet-kimenet kapcsolata minél inkább megegyezik a rendszer bemenetei és kimenetei közötti kapcsolattal. Ha a modellezési feladat valójában csak arra irányul, hogy a rendszer által megvalósított leképezést minél pontosabban adjuk meg, akkor ún. fekete doboz modellezési feladatról beszélünk. A fekete doboz modellezésnél nem törekszünk arra, hogy a modell felépítése kövesse a rendszer felépítését, csupán azt célozzuk, hogy kívülről nézve, tehát adott bemenetekre kapott válaszokat tekintve a modell minél inkább úgy viselkedjen, mint a modellezendő rendszer.

A fekete doboz modellezésnél ennek megfelelően nem használunk a rendszer belső felépítését tükröző ismereteket, kizárólag összetartozó bemeneti és kimeneti adatokból, mintapontokból történik a modell létrehozása.

Egy modell konstrukciójánál először meg kell határozni a modell felépítését, struktúráját, majd meg kell adni a modellben megjelenő szabad paraméterek értékeit. A struktúra rögzítése egy modellosztály rögzítését jelenti, mely modellosztályba tartozó konkrét modellek a szabad paraméterek meghatározása útján nyerhetők.

Neuronhálóknál a modell struktúráját a háló típusa és mérete határozza meg. Ezek rögzítése után a háló tanítása a szabad paraméterek meghatározását jelenti.

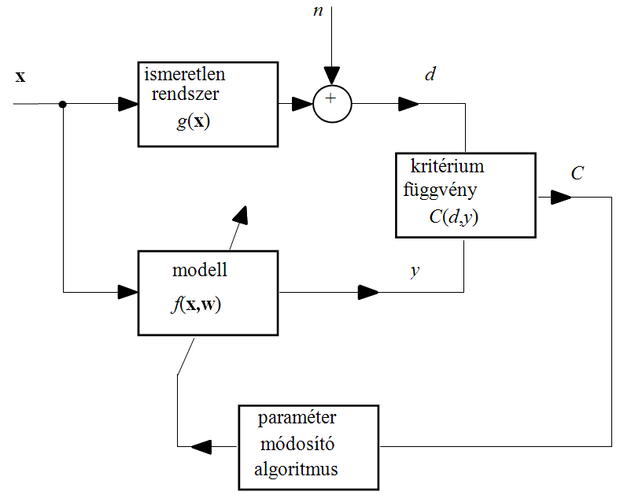
Mint azt az 1. fejezetben láttuk, egyes neuronháló architektúrák univerzális approximátorok, vagyis alkalmasak meglehetősen általános bemenet-kimenet leképezést megadó függvények tetszőleges pontosságú közelítésére. A megfelelő pontosságú approximáció a háló méretének a megválasztásával és a szabad paramétereknek a meghatározásával biztosítható. A háló struktúrájának – típusának és méretének – a meghatározása általában nem része a tanulási folyamatnak, a tanulás a szabad paraméterek meghatározására szolgál. Valójában tehát a tanulássorán egy paraméterbecslési feladattal állunk szemben (2.9 ábra).

A paraméterbecslés során mindig valamilyen cél elérése vagy kritérium teljesítése érdekében kívánjuk az „optimális” paraméterértékeket meghatározni. A tanulási eljáráshoz ezért elsődlegesen egy célfüggvényt vagy kritériumfüggvényt kell megfogalmaznunk. A kritériumfüggvény a modell minőségének a mérésére szolgál, tehát az előzőekben megfogalmazott kockázat épp ilyen kritériumfüggvény szerepet tölthet be, és a kockázat minimalizálása lehet az eljárás célja. A tanulás tehát egy paraméterbecslési eljárásként is felfogható, amikor adott modell struktúra mellett az ismeretlen paramétereket a mintapontok alapján egy kritériumfüggvény szélsőértékének (általában minimumának) elérése érdekében határozzuk meg.

A kritériumfüggvény, továbbá a rendelkezésünkre álló egyéb információ alapján különböző paraméterbecslési eljárásokról beszélhetünk. Amennyiben a kívánt és a tényleges válaszok közötti eltérés négyzetét tekintjük hibafüggvénynek (veszteségfüggvénynek) és az ebből származtatott tapasztalati kockázat minimumát biztosító paramétereket szeretnénk megkapni, legkisebb átlagos négyzetes hibájú (LS) becslésről beszélünk.

LS becslésnéla megoldás a

$C\text{(}w\text{)}=\frac{\text{1}}{l}{\displaystyle \sum _{i=1}^l{\left(d_i-f\text{(}w,x_i\text{)}\right)}^2}$ (2.36)

kritériumfüggvény minimumát biztosító paramétervektor (a keresett paramétervektor becslése: $\widehat{w}$ ). A megoldás tehát

${\widehat{w}}_{\text{LS}}=\text{arg }\underset{w}{\text{min}}C\text{(}w\text{)}$ . (2.37)

Látható, hogy ${\widehat{w}}_{\text{LS}}$ a (2.16) összefüggéssel definiált tapasztalati kockázat minimumát biztosító paramétervektor, ha négyzetes veszteségfüggvényt alkalmazunk. Az LS becslő a megfigyeléseken kívül semmilyen további információt nem használ fel a becslés meghatározásához.

Az adataink, a megfigyelések azonban általában zajosak. Zajos kimenet mellett a bemenet-kimenet leképezést egy $d_i=g\left(x_i\right)+n_i$ kapcsolat írja le (ld. 2.9 ábra). Ha az $n$ megfigyelési zaj statisztikai jellemzése is ismert, a paraméterbecslésnél már valószínűségi megközelítés is alkalmazható. A zaj hatását a $p\text{(}d|x\text{)}$ feltételes sűrűségfüggvénnyel írhatjuk le. Az adatok alapján a g(x) leképezést kívánjuk becsülni, ahol a becslést a modell $y_i=f\left(x_i|w\right)$ leképezése jelenti. Adott x mellett a modell y válasza tehát az f függvénytől (és annak w paramétervektorától) függ. A becslés jóságának mérésére ezért felhasználható a

$\begin{array}{l}p\left(\left\{x_1,\dots ,x_l\right\},\left\{d_1,\dots ,d_l\right\}|f\text{(}{x}_i|w\right)={\displaystyle \prod }_{i=1}^{l}p\left(x_i,d_i|f\text{(}{x}_i|w\text{)}\right)\\ ={\displaystyle \prod }_{i=1}^{l}p\left(d_i|x_i,f\text{(}{x}_i|w\right)p\text{(}{x}_{\text{i}}\text{)}\end{array}$ (2.38)

feltételes sűrűségfüggvény, amely megadja, hogy az $\left(x_1,d_1\right),\left(x_2,d_2\right)\mathrm{,...,}\left(x_l,d_l\right)$ tanító mintapontok milyen valószínűséggel lennének kaphatók, feltéve, hogy a közöttük lévő kapcsolatot egy adott $f\left(x|w\right)$ függvény írja le. Mivel a megfelelő f függvény (illetve a w paramétervektor) meghatározása a cél, és $p\text{(}{x}_i\text{)}$ nem függ f-től, továbbá, ha a bemeneteket egyenletes eloszlással generáljuk, $p\text{(}{x}_i\text{)}$ a (2.38) kifejezés jobb oldalából el is hagyható. Gyakorlati szempontok miatt a szorzat helyett annak negatív logaritmusával érdemes dolgozni. Az így kapott

$L\text{(}w\text{)}=-{\displaystyle \sum _{i=\text{1}}^l\text{ln }p\left(d_i|x_i,f\text{(}{x}_i|w\right)}$ (2.39)

log-likelihood függvény képezi a maximum likelihood (ML) becslés kritériumfüggvényét [Lju99].

A maximum likelihood (ML) becslésolyan paraméterértékeket keres, melyek mellett a rendelkezésre álló megfigyeléseink a legnagyobb valószínűségűek.

${\widehat{w}}_{\text{ML}}=\text{arg }\underset{w}{\text{max}}L\text{(}w\text{)}$ (2.40)

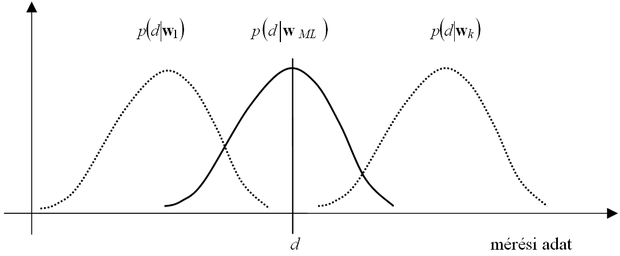
A valószínűség mértékét a paramétervektor függvényében a (log-)likelihood függvény adja meg. A likelihood függvény tehát a megfigyeléseink hihetőségének a mértékeként is értelmezhető. Az ML becslés alapgondolatát illusztrálja a 2.10 ábra.

Az ábra azt mutatja, hogy hogyan befolyásolja a paraméterevektor megválasztása a megfigyelések eloszlását. Azt a paramétervektort fogadjuk el ML becslésnek, mely mellett az aktuális megfigyelésünk (megfigyeléseink), (az ábrán d) a legnagyobb valószínűségű(ek).

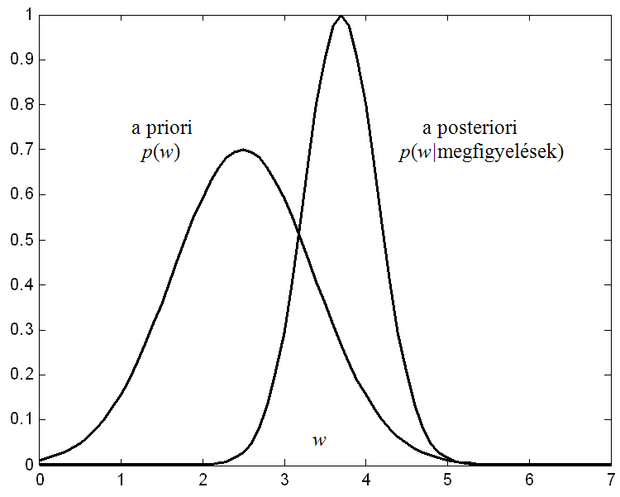
A paramétereink tekinthetők valószínűségi változóknak is. Amennyiben ezen valószínűségi változók eloszlása (sűrűségfüggvénye) ismert, származtatható a Bayes becslés, amelyabból indul ki, hogy az ismeretlen paraméterről van a priori ismeretünk, adott a paraméter ún. a priori eloszlása. Az a priori sűrűségfüggvény azt adja meg, hogy a keresett paraméter a megfigyelésekből származó ismeretek hiányában a paramétertérben milyen értékeket milyen valószínűséggel vehet fel.

A becslési eljárás célja, hogy a paraméterről az ismereteinket pontosítsuk a megfigyelések felhasználásával. Minthogy valószínűségi változóról van szó, a

pontosítás a paraméter eloszlásának pontosítását jelenti. A pontosított eloszlás a megfigyelések felhasználása után nyert eloszlás, amit a posteriori eloszlásnak hívnak. Az a priori és az a posteriori eloszlásokat a Bayes szabály kapcsolja össze:

$p\text{(}w|\text{megfigyelések}\text{)}=\frac{p\text{(megfigyelések}|w\text{)}p\text{(}w\text{)}}{p\text{(megfigyelések)}}$ (2.41)

ahol

_{$p\text{(}w\text{)}$} a paraméter a priori (a megfigyelések előtti) sűrűségfüggvénye,

_{$p\text{(megfigyelések)}$} a kapott megfigyelések (tanító adatok) sűrűségfüggvénye,

$p\text{(}w|\text{megfigyelések}\text{)}$ az a posteriori (a megfigyelések által szolgáltatott ismereteket is figyelembevevő) sűrűségfüggvénye, és

$p\text{(megfigyelések}|w\text{)}$ egy olyan feltételes sűrűségfüggvény, amely azt jellemzi, hogy az adott megfigyelések milyen eloszlásúak, feltéve, hogy azt a w paraméterű modell generálta.

A Bayes becslés az a posteriori sűrűségfüggvény meghatározására vezet. Amennyiben az ismeretlen paraméterről hordoznak információt a megfigyelések (a tanító mintapontok), akkor az a posteriori sűrűségfüggvény a konkrét paraméterérték szűkebb környezetére terjed ki (2.11 ábra).

Az a posteriori sűrűségfüggvény felhasználásával felírható a Bayes kockázat:

$R\text{(}w\text{)}={\displaystyle \underset{z,w}{\overset{}{\int }}L\text{(}z\text{,}w\text{)}}p\text{(}w,z\text{) }dzdw$ (2.42)

ahol p(w,z) a paramétervektor és a megfigyelések együttes sűrűségfüggvénye. A keresett paramétervektor Bayes becslése a Bayes kockázat minimalizálása útján határozható meg:

${\widehat{w}}_{\text{BAYES}}=\text{arg }\underset{w}{\text{min}}R\text{(}w\text{)}$ (2.43)

Az a posteriori sűrűségfüggvény a megfigyelések figyelembevételével a keresett paramétervektor teljes statisztikai leírását adja. A teljes statisztikai ismeretre azonban nincs mindig szükség (ráadásul az a posteriori sűrűségfüggvény meghatározása általában meglehetősen nehéz is), ezért célszerű, ha a lehetséges értékek közül egyet kiválasztunk, és azt tekintjük a Bayes becslésnek. Leggyakrabban ez az a posteriori sűrűségfüggvény maximumához tartozó paraméterérték, amit ezért maximum a posteriori vagy MAP becslésnekis szokás nevezni. A MAP becslés tehát szintén megfogalmazható szélsőérték-keresési problémaként:

${\widehat{w}}_{\text{MAP}}=\text{arg }\underset{w}{\text{max}}p\text{(}w|\text{megfigyelések}\text{)}$ . (2.44)

A Bayes becslés az előző becslési eljárásoknál több információt használ fel. A paraméter sűrűségfüggvényét a legtöbb esetben nem ismerjük, így ilyenkor vagy feltételezéssel élünk (pl. Gauss sűrűségfüggvényt tételezünk fel) vagy a Bayes becslést nem alkalmazhatjuk.

A neuronhálók nagy többségénél a tanulás LS becsléstjelent, hiszen egy négyzetes hibafüggvény minimumát biztosító paraméterértékek meghatározása a cél. Amennyiben a hálóhoz, illetve az általa megvalósított leképezéshez valószínűségi modell is rendelhető, maximum likelihoodvagy Bayes becsléskéntértelmezhető a tanulási folyamat. A valószínűségi megközelítések azzal az előnnyel járnak, hogy az eredmény optimalitásáról határozottabb állítások fogalmazhatók meg, illetve eredményként nem csupán a paraméterek értékét kapjuk meg, hanem ezen értékekhez egy konfidenciaintervallum is rendelhető, így valójában az eredményeknek valamilyen minősítése is megtörténik.