Az eddigiekben láttuk, hogy a tanulás során egy kritériumfüggvény vagy a kockázat funkcionál szélsőértékét keressük, vagyis azt a w értéket, ahol a kritériumfüggvény extremális értéket vesz fel. Szemléletesen a kritériumfüggvény a paramétertér felett egy felülettel jellemezhető – ezt szokás kritériumfelületnek vagy hibafelületnek is nevezni –, és ennek a felületnek a minimumához vagy maximumához tartozó paraméterérték meghatározása a cél. A tanuló eljárások tehátvalójában szélsőérték-kereső eljárások.
A szélsőérték-kereső eljárásoknak egész tárháza áll rendelkezésre, és ezen eljárások szinte mindegyikét alkalmazzák is a neuronhálóknál. Adott neuronháló tanításánál az eljárások széles választékából a megfelelő eljárás kiválasztása számos körülménytől, bizonyos feltételek teljesülésétől vagy hiányától függ. Az egyes eljárások alkalmazhatóságát döntően befolyásolja a kritériumfüggvény jellege. A kritériumfüggvény jellegét egyrészt a veszteségfüggvény, másrészt a tanuló rendszer leképezésének a keresett paraméterektől való függése határozza meg. Kiemelten fontos, ha ez utóbbi kapcsolat lineáris. Ebben az esetben a leggyakrabban alkalmazott négyzetes veszteségfüggvény mellett a kritériumfüggvény a keresett paraméter kvadratikus függvénye, ami − megfelelő feltételek fennállta estén − biztosítja az egyértelmű szélsőérték létezését.
A továbbiakban az egyszerűbb tárgyalás lehetőségének kedvéért általában minimumkeresésről fogunk beszélni, de az eredmények értelemszerűen érvényesíthetők maximumkeresés estére is.
Ha a kritériumfüggvény a keresett paraméter folytonos és differenciálható függvénye, a minimumkeresés során azt a w* értéket keressük, ahol a kritériumfüggvény w szerinti gradiense zérus. A gradiens alapú szélsőérték-kereső eljárásoknak kiemelten fontos szerepük van a neuronhálók tanításánál. Ha gradiens módszerek nem alkalmazhatók, vagy a gradiens analitikus vagy numerikus meghatározása túl bonyolult, kereső eljárásokkal lehet a minimumhelyet meghatározni. A kereső eljárások általában nem tételeznek fel semmit a kritériumfüggvényről. A keresés során valamilyen véletlen vagy determinisztikus algoritmus szerint feltérképezik a W paraméterteret, miközben kiértékelik a hibafelületet. A megoldást a megfelelő szélsőértékhez tartozó w* jelenti.
2.5.1. Gradiens alapú szélsőérték-kereső eljárások
Gradiens alapú eljárásoknál a
(2.45)
feltételt biztosító paraméter meghatározása a cél. A
kritériumfüggvény ismeretében a
megoldása a keresendő paraméterre nézve explicit kifejezést eredményezhet. Ekkor analitikus eredményt kapunk.
Az analitikus kifejezés meghatározása azonban bonyolultabb esetekben, különösen, ha a kritériumfüggvény a keresett paraméter nemlineáris függvénye, komoly matematikai nehézségeket okozhat. Sok esetben a kritériumfüggvényre analitikus kifejezés nem is adható. Ezekben az esetekben iteratív eljárások alkalmazhatók, ahol a tanuló rendszer paramétereit valamilyen algoritmus szerint addig változtatjuk, amíg a kritériumfüggvény minimumát el nem érjük vagy kellő mértékben meg nem közelítjük; vagyis itt a
összefüggésnek megfelelően jutunk a megoldáshoz.
A tanuló eljárások konstrukciója döntően ilyen algoritmusok kidolgozását jelenti, ahol az iteratív eljárás során a mintapontok nyújtotta információt fokozatosan, sok esetben a mintapontok többszöri, ismételt alkalmazása útján használjuk fel. Az iteratív szélsőérték-kereső eljárásoknak is igen széles skáláját dolgozták ki, igazodva a különféle feltételekhez és az eltérő kritériumfüggvényekhez. Ezek nagy részét neurális hálózatoknál is alkalmazni szokták. Leggyakrabban azonban azokat az eljárásokat alkalmazzák, ahol az egy iterációhoz szükséges műveletek száma viszonylag kicsi, és ahol a műveletek egyszerű számításokat igényelnek. A számítások egyszerűségén kívül további követelményeket is ki kell elégíteniük az eljárásoknak.
A fontosabbak követelmények:
-
a konvergencia sebessége legyen minél nagyobb,
-
az eljárás a kritériumfüggvények által meghatározott hibafelületek széles körére, vagyis a feladatok széles osztályára legyen alkalmazható.
A követelmények kielégítése neurális hálózatoknál különösen nehéz, hiszen a szélsőérték-kereső eljárások többségénél a konvergencia csak kvadratikus vagy konvex kritérium-felület mellett bizonyítható és neurális hálózatoknál ezt a feltételt a kritériumfelületek csak kivételes esetben teljesítik.
A neuronhálók döntő többsége nemlineáris bemenet-kimenet leképezést valósít meg. A nemlineáris leképezés a háló paramétereinek szerepét tekintve többféleképpen megvalósítható: a leképezés lehet paramétereiben lineáris vagy nemlineáris. Az előbbi esetben a kapcsolatot
, (2.46)
alakban, az utóbbiban
(2.47)
formában írhatjuk le, ahol mind
, mind ψ(.) valamilyen nemlineáris függvényt jelöl.
Szélsőérték-keresés paramétereiben lineáris modellek esetén
A paramétereiben lineáris modellek a neuronhálók témakörén belül is kitüntetett fontosságúak. Ekkor, továbbá, ha négyzetes hibafüggvényt alkalmazunk, kvadratikus hibafelületet kapunk, amelynek a minimumpontjához tartozó paramétervektor meghatározása a cél.
A négyzetes hibafelületre vonatkozó eljárásokat és eredményeket az
(2.48)
lineáris kapcsolat feltételezésével fogjuk megvizsgálni, de az eredmények értelemszerűen alkalmazhatók a (2.46)-ben megfogalmazott általánosabb kapcsolat esetére is.
Ha kritériumként az átlagos négyzetes hibát tekintjük, a minimalizálandó összefüggés:
(2.49)
ahol
a bemenet autokorrelációs mátrixa,
pedig egy olyan oszlopvektort jelöl, amely a kívánt kimenet és a bemenet közötti keresztkorrelációt mutatja.
A szélsőérték a C(w) négyzetes hiba w szerinti
, (2.50)
parciális deriváltjának nulla értékéhez tartozik, amelyből − amennyiben
létezik − az optimális paraméterkészlet a Wiener-Hopf egyenlet szerint határozható meg:
(2.51)
A (2.51) összefüggés szerint az átlagos négyzetes hiba minimumát biztosító megoldásvektor analitikusan is meghatározható, ha a di kívánt válaszok és az xi bemenetek statisztikai jellemzői, R és p ismertek, ami a gyakorlatban a legritkább esetben teljesül. Ha csak a mintapontok állnak rendelkezésünkre, az analitikus összefüggés alkalmazásához előbb R-et és p-t a véges számú mintapont alapján becsülnünk kell. Ennek, továbbá a (2.51) összefüggés szerinti mátrix invertálásnak az elkerülése érdekében a továbbiakban olyan módszereket fogunk vizsgálni, amelyek vagy eleve kevesebb ismeret meglétét igénylik, vagy amelyek a tanítópontokból iteratív úton igyekeznek minél több ismeretet összegyűjteni (pontosítani).
Mielőtt azonban ezekre rátérnénk, a [Wid85] irodalmat követve bemutatjuk a fentiekben vázolt, ideálisnak tekinthető megoldás néhány lényeges tulajdonságát.
Először a (2.51) összefüggést a (2.49) hibakifejezésbe helyettesítve megkapjuk az elérhető négyzetes hiba minimumát:
(2.52)
Sokszor előnyös, ha egy paraméter tényleges értéke helyett az ideális paraméter-értéktől való eltéréssel, azaz a paraméter-hibával dolgozunk. Ezért alakítsuk át ennek megfelelően a (2.49) összefüggést (2.52) felhasználásával. A hiba
(2.53)
alakba írható, ahol
. A (2.53) összefüggés jól mutatja, hogy a kritériumfüggvény a W paramétertér felett egy kvadratikus hibafelülettel jellemezhető, amelynek − ha R pozitív definit − a
mellett minimumpontja van.
A (2.49) és a (2.53) összefüggésekből kiindulva ebben a formába is felírható a gradiens vektor:
(2.54)
A négyzetes kritériumfüggvény tulajdonságai
Az átlagos négyzetes hiba (2.53) szerinti összefüggése tömör formában jelzi, hogy a kritériumfüggvény paraboloid hibafelületet ír le, melynek jellemzőit az R mátrix határozza meg. Ebből egyértelműen arra a következtetésre juthatunk, hogy a (2.49) összefüggéssel definiált hiba a négyzetes jelleg megtartása mellett csak a bemeneti jeltől, pontosabban annak korrelációs mátrixától függ. A későbbiekben látni fogjuk, hogy a szélsőérték-kereső eljárások hatékonyságát befolyásolják a hibafelület tulajdonságai − a hibafelület alakja −, ezért ezzel a kérdéssel most kiemelten foglalkozunk.
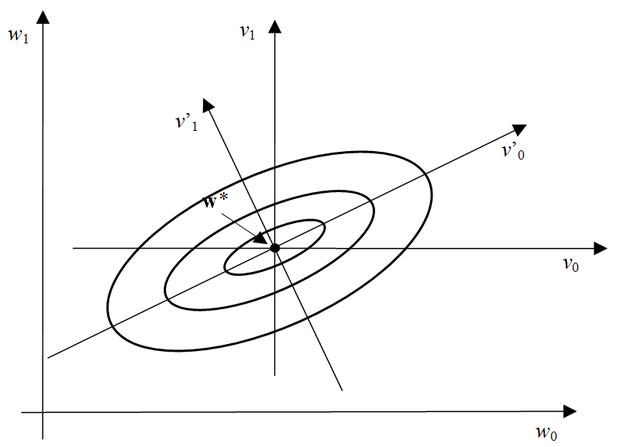
Elsőként − kétdimenziós paramétertér feltételezése mellett − gondolatban rajzoljuk fel a paraméterek síkján a (2.53) összefüggés szerinti hibafelület "szintvonalait". A szintvonalak − az ún. izokritérium görbék − egy görbesereget alkotnak. A görbesereg egy eleme − egy izokritérium görbe − azon pontok mértani helyét adja meg, amelyekhez (egy adott) állandó kritériumfüggvény-érték tartozik. Minden ilyen görbe egy-egy ellipszist jelöl ki, amely a síkban általános helyzetben (de egymáshoz képest kötötten), helyezkedik el a sík koordináta tengelyeihez képest. Egy ilyen ellipszis előállítható úgy is, hogy a paraboloid hibafelületet egy, a paraméterek síkjával párhuzamos, ettől a síktól a rögzített négyzetes hiba értéknek megfelelő távolságra lévő síkkal elmetszünk. Különböző hibaértékekhez különböző, de koncentrikus, azaz olyan ellipsziseket kapunk, melyek főtengely irányai egybeesnek (ld. 2.12 ábra). Ez a geometriai kép tetszőleges dimenzióra általánosítható. Könnyen belátható, hogy a metszék-ellipszisek (ill. ellipszoidok) főtengelyei kitüntetett irányok. A hibafelület ezen irányokban található bármely pontjánál ugyanis a gradiens irányok egybeesnek a főtengely irányokkal, azaz mindig a középpont felé mutatnak. Így ezen pontokból kiindulva a gradiensek mentén közvetlenül a középpont felé mozoghatunk, illetve ennek megfelelően a hibafelületen a minimumhely felé "ereszkedhetünk". A mértani helyet tovább vizsgálva arra az érdekes következtetésre juthatunk, hogy a főtengely irányokat az R mátrix sajátvektorai jelölik ki, tehát a későbbiekben jól felhasználható eredményre vezet az R mátrix sajátérték/sajátvektor rendszere. Ha feltesszük, hogy a sajátértékek multiplicitása egy és az R mátrix egy N×N-es mátrix (N a bemeneti vektorok dimenziója), akkor R felírható az alábbi formában
, (2.55)
ahol
a sajátértékekből képezett diagonál mátrix, Q pedig a sajátvektorok mátrixa. Ha a sajátvektorokat egységnyi hosszúságúra normáljuk, és felhasználjuk azt a tulajdonságot, hogy a szimmetrikus négyzetes mátrixok sajátvektorai ortogonálisak (vagyis Q ortonormált), akkor:
(2.56)
Behelyettesítve a (2.56) kifejezést a (2.53) összefüggésbe, a hibára
(2.57)
adódik. Az új kifejezésben v'-t egy forgatási transzformációval kaphatjuk meg v-ből, amit értelmezhetünk úgy, hogy a hibafelület "alatt" elforgattuk a paraméterek koordináta-rendszerét olyan mértékben, hogy a koordinátatengelyek éppen főtengely irányúak legyenek. Ebben a koordinátarendszerben a (2.54) összefüggésnek megfelelő gradiens vektor a következőre adódik:
(2.58)
A gradiens komponensei tehát a megfelelő sajátértékek és a paraméterhiba-komponensek szorzataként számíthatók. A sajátértékekhez szemléletes jelentés is rendelhető, ugyanis a főtengely-irányokban számított második derivált komponensek az R mátrix sajátértékeinek kétszeresei lesznek:
.
(2.59)
Mindezekből képet alkothatunk a paraboloid hibafelület geometriai tulajdonságairól. Ha a bemeneti jel autokorrelációs mátrixának sajátértékei jelentősen eltérnek egymástól, akkor a paraboloid hibafelület a különböző főtengely irányokban is jelentősen eltérő meredekségű lesz. Ez a tulajdonság − mint látni fogjuk − általában kedvezőtlen az ún. gradiens-alapú szélsőérték-kereső eljárások szempontjából. A 2.12 ábra nemcsak a hibafelületet jellemző izokritérium görbéket, hanem a w, v és v’ koordinátarendszereket is mutatja.
Szélsőérték-keresés Newton módszerrel.
Ha a gradiens
(2.60)
szerinti felírását balról megszorozzuk
-gyel, akkor átrendezés után a
(2.61)
alakot kapjuk, amely négyzetes hibafelület esetén tetszőleges kiinduló w mellett közvetlenül megadja az optimális megoldást.
Ha a hibafelület nem négyzetes, a (2.61) összefüggés akkor is alkalmas kiindulás egy iteratív eljárásra. (Nem kvadratikus függvényeknél tekinthetjük úgy, mintha ezek másodfokú Taylor-sorával dolgoznánk, annál is inkább, mivel a megoldás − a minimumhely − közelében a nem másodfokú függvények jó közelítéssel úgy viselkednek, mint a négyzetes függvények.) Az iteratív eljárásoknál lépésenként módosítjuk a megoldást: az épp érvényes megoldásból kiindulva, annak korrekciójával kapjuk a következő lépés érvényes megoldását.
A Newton eljárás iteratív összefüggése, ha az egyes iterációs lépések indexét k-val jelöljük
. (2.62)
ahol
a gradiensvektort jelöli a k-adik lépésben érvényes paramétervektor mellett, míg 0 < μ < 1 az ún. tanulási tényező (learning rate), amelyet négyzetes esetben az egylépéses konvergenciához 1/2-re kell választani. Megjegyezzük, hogy a μ tanulási tényezőt bátorsági tényezőnek is szokás nevezni, mivel értéke befolyásolja, hogy adott gradiens irányában mekkora lépésekben haladunk. Ha az utóbbi összefüggésben visszaírjuk a derivált (2.60) szerinti alakját, és mindkét oldalból levonjuk w*-ot, akkor a
(2.63)
összefüggést, illetve az ennek megfelelő
(2.64)
iterációs kapcsolatot kapjuk, amely konvergens, ha 0 < μ < 1, és négyzetes hibafelületnél egy lépésben optimumot ad, ha
.
Szélsőérték-keresés a "legmeredekebb lejtő" (steepest descent) módszerével
Ez a módszer a negatív gradiens irányában"ereszkedik" a hibafelületen. Iteratív összefüggése:
(2.65)
A (2.65) összefüggésben a fentiekhez hasonlóan visszaírva a gradiens (2.60) szerinti alakját, és ismét mindkét oldalból levonva
-ot, a
, (2.66)
illetve az ennek megfelelő
(2.67)
összefüggést kapjuk. Ez utóbbi kifejezésből látható, hogy ennél az eljárásnál a μ tanulási tényező megválasztása függ R-től. Ha áttérünk a főtengely-irányú koordinátákra, mint ahogy azt korábban a (2.57) összefüggésben tettük, akkor (2.67) helyére a
(2.68)
összefüggés írható, amely lehetővé teszi, hogy a paraméter-hibákat komponensenként vizsgáljuk. A (2.68) összefüggésből jól látható, hogy a konvergencia feltétele ekkor:
, (2.69)
ahol
R legnagyobb sajátértéke.
A (2.62), és (2.65) összefüggések összevetéséből látszik, hogy a Newton módszer szerinti iterációban elkerülhetetlen R ismerete, míg a gradiens menti iteráció R ismeretét közvetlenül nem igényli. A μ tanulási tényező helyes megválasztásához azonban mégis kell valamennyi ismeret a bemeneti jelről. Sokszor megfelelő a
(2.70)
összefüggés használata, amellyel a
(2.71)
előírás adódik, ahol tr(R), az autokorrelációs mátrix nyoma, amelyet a mintapontokból az alábbi módon becsülhetünk:
. (2.72)
Itt xij az i-edik bemeneti vektor j-edik komponense (i=1, 2, …, l ; j=1, 2, …, N). A tanulási tényező megválasztása a szélsőérték-keresés igen kritikus lépése, mert közvetlenül befolyásolja az eljárás stabilitását, ill. a konvergencia sebességét.
A (2.69) összefüggésből látható, hogy a konvergencia sebessége a bemeneti jel korrelációs mátrixától, pontosabban annak sajátértékeitől függ. Az is látható, hogy az eljárás konvergenciájának biztosításához a tanulási tényezőre felső korlát adható. A felső korlát azonban valóban csak a konvergencia tényét garantálja, miközben az eljárás gyakorlati alkalmazása szempontjából a konvergencia sebessége is fontos.
Az előzőekben láttuk, hogy a
sajátértékekhez szemléletes jelentés is rendelhető. A paraboloid hibafelület főtengely irányait R sajátvektorai adják meg. Az i-edik sajátvektor, qi irányában a hibafelület második deriváltja viszont arányos a sajátvektorhoz tartozó
sajátértékkel. Minél nagyobb egy sajátérték, annál nagyobb a hibafelület adott irány menti meredekség-változása, azaz a görbülete. A konvergenciára vonatkozó (2.69) összefüggés a konvergencia tényét még a hibafelület legmeredekebb iránya mentén is garantálja, viszont más irányok mentén még nagyobb μ mellett is garantált lenne a konvergencia. A főtengely irányok mentén az adott sajátvektorhoz tartozó sajátérték reciproka jelenti a konvergenciát még biztosító tanulási tényező felső korlátját.
A (2.69) által megfogalmazott korlát betartása azért szükséges, mert általában nem ismerjük, hogy a hibafelület mely pontjából indulunk ki, így a konvergencia csak akkor garantálható, ha az a kiindulási ponttól függetlenül minden körülmény mellett fennáll. A hibafelület kevésbé meredek részein a túl kis tanulási tényező ugyanakkor a lehetségesnél kisebb konvergencia-sebesség elérését eredményezi. A konvergencia-sebesség szempontjából tehát az a kedvező, ha a sajátértékek egyformák vagy közel azonosak, vagyis ha
. Különösen kedvezőtlen esettel állunk szemben, ha a legkisebb és a legnagyobb sajátértékek aránya,
. Ez egy keskeny hibafelületet jelent. Keskeny hibafelületnél kedvezőtlen kiinduló pont mellett a konvergencia nagyon lassú is lehet.
Felmerül a kérdés, hogy ilyen esetekben lehet-e valami olyan módosítást tenni, ami a konvergencia-sebesség növelését eredményezi. A válasz pozitív. Ha a bemeneteket olyan módon transzformáljuk, hogy a transzformált bemenetek autokorrelációs mátrixa közel egységmátrix, a sajátértékek közel egyformák lesznek, így kiindulóponttól függetlenül a legkedvezőbb tanulási tényező választható. Ennél a megoldásnál a legmeredekebb lejtő gradiens eljárást a „transzformált” térben végezzük. A módszer részletesebb bemutatását a későbbiekben a transzformált tartománybeli LMS eljárásnál adjuk meg.
A konjugált gradiensek módszere
A (2.51) összefüggés a w paraméterekre nézve egy lineáris egyenletrendszer megoldása, amelyhez az R mátrix inverze szükséges. Az
(2.73)
egyenlet megoldása egyszerűsíthető az ún. konjugált irányok ismeretében. A konjugált irányokat azok a
vektorok jelölik ki, amelyekre fennáll, hogy
(2.74)
Könnyen belátható, hogy a
vektorok lineárisan függetlenek és egy olyan bázist alkotnak, amely kifeszíti a
paraméterek terét, így segítségükkel előállítható a paraméterek terének az a vektora is, amely a
vektorból elvezet a
vektorba:
(2.75)
Itt
a lineáris kombináció súlytényező készletét jelöli. Ha a (2.75) összefüggés mindkét oldalát megszorozzuk balról
-rel, és
helyére behelyettesítjük p-t ((2.73) alapján), akkor a konjugált irányok (2.74) feltétele miatt az
-re nézve N-ismeretlenes lineáris (2.75) egyenletrendszer "szétesik", és
-k közvetlenül megadhatók lesznek (és egyben nyilvánvalóvá válik a konjugált q vektorok használatának az előnye is):
. (2.76)
Ezek után definiálhatunk egy iteratív eljárást w(k+1) számítására:
(2.77)
ahol
(2.78)
tehát N lépésben elérjük az optimumot.
A (2.77) összefüggésben szereplő
tényező egy alternatív kifejezése nyerhető, ha felhasználjuk a (2.74) és (2.78) összefüggéseket annak igazolására, hogy
(2.79)
Ekkor ugyanis a (2.76) összefüggésben w(0) w(j)-re cserélhető, és így (2.60) felhasználásával
(2.80)
adódik.
A
konjugált gradiens irányok meghatározása iteratívan történik úgy, hogy a kezdőérték
, azaz a kezdőpontban érvényes negatív gradiens adja a legelső irányt, majd a következő irányok rendre az aktuális gradiens és a megelőző irány lineáris kombinációjaként kerülnek kiszámításra:
(2.81)
Ha ezt a kifejezést jobbról megszorozzuk
-val, megkapjuk
ahhoz szükséges új értékét, hogy az új irány konjugált irány legyen:
(2.82)
Mivel (2.60) és (2.77) felhasználásával
(2.83)
a (2.82) összefüggésből
kiejthető és így
-ra a következő kapható
. (2.84)
Az algoritmus tehát a kezdőpontbeli negatív gradiens, mint kezdeti irány választása mellett számolja az új paramétert a (2.77) egyenlet szerint úgy, hogy olyan
értéket vesz, melynél a hibakritérium értéke minimális (az
szerinti derivált nulla; ún. vonalmenti keresés, line search módszer). Erre azért van szükség, mert az esetek többségében R ismeretének hiányában
(2.80) alapján nem számolható közvetlenül. Ezután az új paraméterhez tartozó gradienst számítjuk, amelynek birtokában (2.82) alapján új
-t határozunk meg. Ezzel az új irány (2.81)-ból számítható.
Meg kell jegyezni, hogy a
együtthatók meghatározására léteznek egyéb módszerek is, melyek más kifejezésre vezetnek. Ennek jelentősége abban rejlik, hogy azon esetben, ha az egymás után következő gradiensek különbsége nullává válik (vagyis az (2.84) szerinti összefüggés használhatatlan lesz a nevező nullává válása miatt), a konjugált gradiens módszer akkor is használható a
-kra vonatkozó más kifejezés alkalmazásával. Vizsgálatokat végeztek annak meghatározására is, hogy különböző feladattípusoknál a
-k meghatározásának melyik módszere a legjobb.
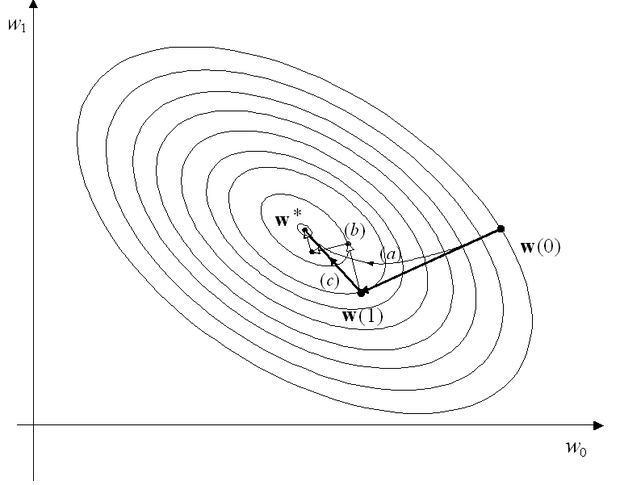
A módszer fontos jellemzője, hogy kvadratikus, N-dimenziós kritériumfelület esetén a (2.78) összefüggés értelmében a konjugált gradiensek módszere N lépésben konvergál. A gyorsabb konvergencia annak tudható be, hogy minden egyes lépésnél a (2.77), (2.78) és (2.80) egyenletek által meghatározott új w(k) a (2.49) egyenletben definiált négyzetes hibafüggvényt minimalizálja w szerint az addigi irányok (q0, q1,...,qk) által kifeszített altér felett. (Bizonyítható, hogy az algoritmus szerint számított gradiens irányok mindig merőlegesek a korábbi lépésekben meghatározott q irányokra. Ebből az ortogonalitásból pedig következik az előbbi kijelentés [Joh92]. Ezzel szemben a többi gradiens alapú eljárásnál, mint pl. a legmeredekebb lejtő módszernél, az új irány menti minimalizálás ″leronthatja″ a korábbiak hatását. Ezt illusztrálja a 2.13 ábra, ahol a konjugált gradiens módszeren (c) kívül a legmeredekebb lejtő módszer esetére is láthatunk két példát. Amennyiben a lépésnagyság az egyes iterációknál kicsi (kis μ tanulási tényezőt használunk), sok lépésben, de a trajektória (az ideális útvonal) mentén közelítjük meg a minimumhelyet (a), míg nagyobb lépésnagyság mellett láthatóan felesleges paraméterváltoztatásokra is sor kerül (b).
Összefoglalva az algoritmus a következő iterációs lépésekből áll:
-
Válasszunk egy kezdeti pontot: k=0, w(0), és határozzuk meg ebben a pontban a kritériumfelület gradiensét (
2.
12. ).
-
Ha
15.
25. =0, szélsőértékre jutottunk, állítsuk le az eljárást, egyébként legyen
27.
41. .
-
Határozzuk meg a megfelelő lépésnagyságot (
44.
56. ), és számítsuk ki az új súlyértéket (2.80)-nek, ill. (2.77)-nek megfelelően. Amennyiben R nem áll rendelkezésünkre,
58.
70. (2.80) alapján nem határozható meg. Ilyenkor
72.
84. meghatározására azt a tényt használjuk ki, hogy megfelelő lépésnagyság választás esetén
86.
98. irányban elmozdulva a kritériumfelületen feltételes szélsőértéket érünk el, vagyis:
-
Végezzük el a súlymódosítást, és az új pontban határozzuk meg az új gradiens,
101.
113. értékét. Ha
115.
127. =0, állítsuk le, egyébként folytassuk az eljárást.
-
A (2.81) és (2.84) összefüggések felhasználásával határozzuk meg az új konjugált irány,
130.
144. értékét.
-
Ha k=N, az eljárásnak vége, egyébként növeljük meg k értékét: k=k+1, és folytassuk az eljárást a 3. lépéssel.
A konjugált gradiens eljárást, vagy az eljárás valamilyen változatát kedvező konvergencia tulajdonságai miatt gyakran alkalmazzák neuronhálók tanításánál. Egyes neuronhálóknál kedvelt az ún. momentum módszer, amely a konjugált gradiens eljáráshoz hasonló heurisztikus gradiens alapú eljárás. A hasonlóság abban áll, hogy a paramétermódosítás adott iterációbeli iránya itt is a gradiens és az előző iterációban alkalmazott irány súlyozott összegeként határozható meg. A módosítás irányának meghatározása tehát itt is a (2.81) összefüggéshez formailag hasonló módon történik, azzal a különbséggel, hogy a súlyozó együtthatók meghatározása nem (2.84) alapján, hanem tapasztalati úton történik. Ennek megfelelően a momentum módszer egyes lépéseiben használt irányok nem is lesznek konjugált irányok. A momentum módszerrel részletesebben a 4. fejezetben foglakozunk.
Az LMS algoritmus és néhány változata
Az eddigi eljárások mind a (2.49) összefüggésben definiált hibakritériumból, vagyis a négyzetes hiba várható értékéből indultak ki. A várhatóérték-képzés következtében a kapott eljárások közvetlen vagy közvetett formában igényelték az R autokorrelációs mátrix ismeretét. Neuronhálóknál általában a tanító mintapont-készleten kívül más ismeretünk nincs, így az autokorrelációs mátrix is csak a mintapontokból becsülhető. A becslés viszonylag nagy számításigénye, továbbá az R mátrixszal történő további műveletek számításigénye miatt hatékonyabb lenne egy olyan eljárás, ami R ismerete nélkül is alkalmazható. A Bernard Widrow által javasolt LMS (Least Mean Squares) algoritmus épp ezt teszi. Az LMS algoritmus és az eddigi gradiens alapú eljárásokközötti alapvető különbség az, hogy az LMS eljárás a (2.49)-ben definiált átlagos négyzetes hiba, mint kritériumfüggvény helyett a pillanatnyi hiba alapján dolgozik.
Az LMS eljárásnál a hibakritériumot, mint a pillanatnyi hiba négyzetét definiáljuk:
. (2.85)
A pillanatnyi hiba alapján – gradiens módszert alkalmazva – a paramétermódosítás a kritériumfüggvény „pillanatnyi” gradiense alapján történhet.
(2.86)
Az LMS eljárás alapgondolata tehát az, hogy az átlagos négyzetes hiba helyett a pillanatnyi négyzetes hibából indulunk ki. Természetesen meg kell vizsgálnunk, hogy a várhatóérték-képzés elhagyásának milyen következményei lesznek.
Könnyen belátható, hogy (2.86) várható értéke megegyezik a gradiens vektor (2.54) összefüggésével [Wid85]. A pillanatnyi gradiens vektorral a "legmeredekebb lejtő" módszert alkalmazva a paraméter változtatás összefüggésére a következőt kapjuk:
. (2.87)
Az is megmutatható, hogy a paraméterváltoztatás eredményeképpen kapott megoldás várható értéke
(2.88)
amelyből, ha áttérünk az R sajátvektorai által meghatározott koordinátarendszerre, adódik, hogy
(2.89)
Fentiekből látszik, hogy ha k minden határon túl nő, az LMS megoldás várható értéke megegyezik az optimális megoldással (ami a zérus vektor a sajátvektor koordináta-rendszerben, vagyis az eredeti koordinátarendszerben épp a
), ha (2.89) jobb oldala nullához konvergál. E feltétel pedig azonos a legmeredekebb lejtő módszer konvergenciájának (2.69)-ben megfogalmazott feltételével, vagyis a tanulási tényezőre vonatkozó konvergencia-feltétel az LMS algoritmusnál is
. (2.90)
Az LMS eljárás legnagyobb előnye az eddig látott eljárásokkal szemben, hogy alkalmazásához a mintapontokon kívül másra nincs szükség, továbbá, hogy nagyon egyszerűen megvalósítható. Az eljárás egyszerűsége mellett azonban azt is látni kell, hogy a konvergencia feltételének megfelelő tanulási tényező megválasztásához itt is ismerni kell
-ot (vagy legalább annak (2.70) alapján nyerhető felső becslését), sőt a megfelelően gyors konvergenciához most is szükség van arra, hogy a
/
1 arány teljesüljön. Meg kell jegyezni, hogy a sajátértékek becslésének viszonylag nagy számításigénye miatt a gyakorlati alkalmazások többségében a tanulási tényezőt tapasztalati úton határozzák meg.
Rendkívüli egyszerűsége következtében az LMS eljárást igen elterjedten használják. Az a tény azonban, hogy minden lépésben a pillanatnyi gradiens irányában korrigálunk, az optimum közelében problémákat okozhat. E problémák jellegét érzékelhetjük, ha az ideális gradienstől való eltérés statisztikai jellemzőit vizsgáljuk. Az eltérést modellezzük egy
zaj folyamattal, amivel
(2.91)
Ha elegendően kicsi μ tanulási tényezővel dolgozunk, akkor elég jól megközelíthetjük az optimális
értéket, ahol már
, így
. (2.92)
Az
zaj kovarianciája
(2.93)
A (2.51) összefüggés segítségével és felhasználva, hogy
(2.94)
belátható, hogy az optimum közelében
, ezért (2.93) átírható a következő alakba:
(2.95)
Ha ennek a varianciának a hatását nyomon követjük az iterációk során, akkor a paraméter hiba-vektor (v(k)) kovarianciáját is becsülhetjük. A levezetés részletezése nélkül
(2.96)
azaz a paraméter hiba kovarianciavektora egyenesen arányos a tanulási tényezővel, ami azt jelenti, hogy a varianciát úgy tudjuk alacsony szinten tartani, hogy az optimum közelében kis μ értékkel dolgozunk.
A paraméter hiba kovarianciája a 2.14 ábrán látható módon lehetetlenné teszi a minimum elérését. A paraboloid hibafelület tulajdonságai következtében ugyanis a bekövetkező hibának nem
a várható értéke. A (2.57) összefüggésre alapozva és felhasználva a
(2.52) összefüggését a
-t meghaladó komponensre − az ún. többlet átlagos négyzetes hibára (excess mean-square error, EMSE) − a következő adódik:
, (2.97)
amelynek felhasználásával a hiba elérhető minimuma
(2.98)
lesz. A pillanatnyi gradiens alkalmazásának következménye önmagában is kifejezhető:
(2.99)
M értékét, amelyet az irodalomban „beállítatlanságnak” (misadjustment) neveznek, tehát a többlet hibának és a Wiener-Hopf megoldáshoz tartozó hibának (a minimális átlagos négyzetes hibának) az arányaként definiáljuk.
A továbbiakban az LMS eljárás néhány további változatával foglalkozunk: előbb az LMS és a Newton algoritmus ötvözeteként származtatható algoritmust mutatjuk be röviden, majd egy olyan változat főbb jellemzőit foglaljuk össze, amelynek során egy kedvezőtlen konvergencia tulajdonságú eset a bemeneti mintatér transzformálásával kedvezőbb esetté alakítható.
Ez az algoritmus a Newton és az LMS algoritmus egyes elemeit együttesen magába építi. A Newton algoritmus paramétermódosító algoritmusát a (2.62) összefüggés adta meg és láttuk, hogy amennyiben mind a gradiens, mind
ismert, akkor egy lépésben is elérhető a w* megoldás. Ha
-et nem ismerjük, és az iterációnkénti pontos gradiens helyett csak a pillanatnyi gradiens áll rendelkezésünkre, akkor az LMS eljárás alkalmazható. Az LMS/Newton algoritmusnálfeltételezzük, hogy
ismert, de a pillanatnyi gradiens alapján számolunk. Így az iterációs összefüggés a (2.62) és a (2.86) összefüggések kombinálásából származtatható, vagyis a Newton algoritmusban a gradiens értékét a pillanatnyi gradienssel helyettesítjük:
. (2.100)
A kapott összefüggés csak annyiban tér el az LMS algoritmustól, hogy a súlymódosító részben
is szerepel. Ha R azonos
sajátértékekkel rendelkező diagonálmátrix lenne, akkor
=I-re adódna, vagyis, ha μ helyett
μ-t használnánk, lényegében visszakapnánk az LMS algoritmust, ahol μ-t a sajátérték reciprokánál kisebbre kell választanunk. Alkalmazzuk ezt a választást akkor is, ha
nem diagonálmátrix, sőt a sajátértékek sem egyformák. Ekkor legyen
az R mátrix sajátértékeinek az átlaga. Az így kapott algoritmus az LMS/Newton algoritmus:
. (2.101)
Mindamellett, hogy az LMS/Newton algoritmust kedvező tulajdonságai miatt szokták "ideális adaptív algoritmusnak" is nevezni, a gyakorlati esetek többségében nem alkalmazható, mert
pontos ismeretét igényli. Létezik azonban olyan, a gyakorlatban is használható módosítása, amelyben rekurzívan becsüljük az
, ill.
mátrixot. A (2.100) összefüggés módosításával
(2.102)
ahol (
feltételezésével)
(2.103)
a korrelációs mátrix becsült értéke a (k+1)-edik időpillanatban,
pedig az ún. mátrix inverziós lemma (ld. Függelék) felhasználásával az alábbi formában adható meg:
. (2.104)
A (2.103) összefüggésben szereplő konstansok kapcsolata gyakran
. (Továbbá gyakori ajánlás η-ra a [0.9...0.99] közötti érték). A (2.102)-(2.104) összefüggésekkel jellemzett algoritmusnak léteznek további változatai, amelyek között érdemi különbség csak az R mátrix rekurzív becslésében van. Formai szempontból a (2.102)-(2.104) összefüggések az iteratív, gradiens alapú szélsőérték-kereső eljárások széles családját lefedik.
Transzformált tartománybeli LMS eljárás
A legmeredekebb lejtő módszer tárgyalásánál láttuk, hogy a konvergencia-sebességet az R mátrix sajátértékeinek alakulása nagymértékben befolyásolja. A konvergencia-sebesség szempontjából a legkedvezőbb eset, ha az összes sajátérték azonos, és különösen kedvezőtlen, ha a legkisebb és a legnagyobb sajátérték nagymértékben különböző, vagyis ha
. Láttuk azt is, hogy a konvergencia-sebesség szempontjából azért kedvezőtlen a sajátértékek nagyfokú különbözősége, mert ilyenkor a hibafelület különböző részein a felület meredeksége jelentősen eltér, így a
alapján választott tanulási tényező – bár a konvergenciát biztosítja – az esetek jelentős részében a szükségesnél óvatosabb lépések megtételét eredményezi. Minél meredekebb szakaszán mozgunk a hibafelületnek, annál kisebb a megengedhető μ. Ha nem tudjuk, hogy a hibafelület mely szakaszán haladunk, akkor a μ megválasztása szempontjából a legrosszabb esetet kell feltételeznünk, vagyis azt, mintha a felület legmeredekebb részén mozognánk. Ezt fejezi ki a (2.69) összefüggéssel megadott felső korlát, amely szerint μ -t a legnagyobb sajátérték reciprokánál kisebbre kell választani.
A hibafelület alakját az R mátrix jellemzi, ami a bemeneti mintákból számítható. A konvergencia-sebesség szempontjából kedvezőbb helyzet tehát úgy teremthető, ha a bemeneteket módosítjuk. A módosításnak arra kell irányulnia, hogy a módosított bemenetek autokorrelációs mátrixa minél inkább az egységmátrix legyen. A bemenetek módosítása valamilyen alkalmas transzformációval lehetséges. A transzformáció az
bemeneti mintapontokból
transzformált mintapontokat állít elő. A transzformáció következtében természetesen az eredeti probléma megoldásában szerepet játszó w paramétervektor helyett az ugyancsak megfelelő módon transzformált w’ paramétervektor fog szerepelni [Nar83].
A szélsőérték-keresési probléma a transzformált bemenetekre is megfogalmazható, így az eddig bemutatott eljárások mindegyike alkalmazható transzformált esetben is.
Megfelelően választott transzformációt és azt követő normalizálást alkalmazva biztosítható a
arány. Jelölje T az x(k) és X(k) közötti transzformációt leíró mátrixot:
X(k)=Tx(k). (2.105)
Ha a kiinduló bemenetek autokorrelációs mátrixa
, a transzformált bemenetek autokorrelációs mátrixát
(2.106)
formában kapjuk (a kétféle autokorrelációs mátrix megkülönböztetése miatt alkalmazzuk a bemenet autokorrelációs mátrixára az
jelölést az eddigi R helyett és az
jelölést a transzformált bementek autokorrelációs mátrixára). Legyen T egy ortonormált transzformáció, vagyis teljesüljön a TTT=I összefüggés. Ha még azt is előírjuk, hogy T=QT, ahol Q az
mátrix normált sajátvektoraiból képezett mátrix, akkor (2.55)-et figyelembevéve
, (2.107)
vagyis a transzformált bemenetek autokorrelációs mátrixa az
sajátértékeiből képezett diagonálmátrix. A diagonálmátrixból egységmátrix megfelelő normalizálással nyerhető. Ezért, ha a transzformáció mátrixát
-ra választjuk, a transzformált bemenet autokorrelációs mátrixára
(2.108)
adódik, vagyis minden sajátérték azonos és egységnyi lesz.
Az autokorrelációs mátrix sajátvektoraiból képezett Q mátrixszal elvégzett ún. főtengely transzformációt Karhunen-Loève transzformációnak (KL transzformáció, KLT) is nevezik. A kitűzött feladat szempontjából ez az optimális transzformáció, hiszen ha a főtengely transzformáció után a sajátértékek reciprokával (2.108) szerint még normalizálunk is, a kitűzött célt el is érjük, a sajátvektorok azonosak lesznek.
A konvergencia-sebesség növelésére a KL transzformációt, annak viszonylag jelentős számításigénye miatt, ritkán használják. Helyette könnyebben számítható ortogonális transzformációkat, például a diszkrét Fourier transzformációt vagy a diszkrét koszinusz transzformációt szokás alkalmazni. Ha a KL transzformációtól eltérő ortogonális transzformációt alkalmazzuk, meg kell vizsgálnunk, hogy ennek milyen hatása lesz a
arány alakulására.
Írjuk fel ehhez komponensenként a transzformált tartománybeli LMS eljárás súlymódosítását:
(2.109)
ahol a
értékek a transzformált tartománybeli súlyokat jelölik. A súlymódosításnál most minden komponens esetén más-más tanulási tényezőt (
) alkalmazhatunk. Ha a
(2.110)
választással élünk, akkor ez a transzformált tartományban normálást is jelent.
A súlymódosítást vektorosan is felírhatjuk, ha bevezetjük a
N × N-es diagonálmátrixot, melynek az (i,i)-dik eleme
.
. (2.111)
A transzformált tartományban a konvergencia sebessége
sajátértékeinek szóródásától vagy a legnagyobb és legkisebb sajátértékének arányától függ.
Ennek az aránynak a becsléséhez felhasználjuk, hogy egy A mátrix
aránya felülről becsülhető:
, (2.112)
mivel az A mátrix maximális sajátértéke a mátrix nyomával majorálható, minimális sajátértéke pedig a mátrix determinánsával minorálható:
, (2.113)
illetve, ha N>2
. (2.114)
Ha feltételezzük, hogy
, akkor
, (2.115)
továbbá
. (2.116)
és
. (2.117)
Mivel
, ezért feltételezhető, hogy
legfeljebb 1 lehet, ezért
, (2.118)
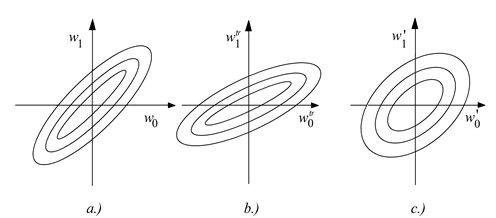
tehát megfelelően megválasztott transzformációnál – bár (2.118) erre feltétlen garancát nem ad – esély van arra, hogy a sajátérték-arány csökkenjen és így kedvezőbb feltételeket biztosítson a gyorsabb konvergenciához. A transzformált tartományra való áttérés hatását illusztrálja a 2.15 ábra.
Az ábra a hibafelület izokritérium görbéit mutatja a paramétertérben az eredeti bemenőjelre (a), a transzformált tartományban, normalizáció nélkül (b) és a transzformált tartományban normalizációval (c). Megjegyezzük, hogy az optimális transzformációt jelentő KL transzformáció esetén a kvadratikus hibafelület izokritérium görbéi koncentrikus körök lesznek.
A fentiek után még azt kell megnéznünk, hogy eredményként mit kapunk, ha a transzformált bemeneti térben alkalmazzuk a legmeredekebb lejtő módszert vagy az LMS algoritmust. Láttuk, hogy az eredeti bemeneti tartományban végzett LMS eljárás a (2.51) Wiener-Hopf egyenlet által megadott súlyvektorhoz tart
. (2.119)
ahol
a bemenet és a kívánt kimenet keresztkorrelációs vektora.
Könnyen belátható, hogy
, (2.120)
ahol
, mint (2.107)-ben megadtuk a transzformált bemenet autokorrelációs mátrixa,
pedig a transzformált bemenet és a kívánt válasz keresztkorrelációs vektora. Tehát a transzformált bemenetekre alkalmazott LMS eljárás eredményeképpen kapott súlyvektor az eredeti súlyvektor transzformáltja lesz.
Szélsőérték-keresés paramétereiben nemlineáris modellek esetén
Az eddigiekben feltételeztük, hogy kvadratikus kritériumfelülettel van dolgunk, amit a legegyszerűbben az
lineáris kapcsolat és a négyzetes hibafüggvény biztosíthat. A súlytér felett azonban akkor is kvadratikus kritériumfelületet kapunk, ha a vizsgált leképezést
alakban adhatjuk meg. Ekkor valójában először a bemeneti vektorok
általi (nemlineáris) transzformációja történik, a transzformált térről a kimeneti térre pedig már lineáris leképezést valósítunk meg. Az optimális paramétervektor meghatározása szempontjából azonban ez az eset nem különbözik az eddig tárgyalttól, hiszen a modellünk most is a paramétervektor lineáris függvénye. Egyes neuronhálók (pl. a radiális bázisfüggvényes – RBF – hálózatok) leképezése ez utóbbi általános formulával írható le, míg más hálóknál – pl. az MLP-knél – a nemlineáris leképezés már a paraméterekben is nemlineáris kapcsolattal történik. Ez utóbbi esetben – még ha négyzetes hibafüggvényt alkalmazunk is – a kritériumfüggvény nem lesz a paraméterek kvadratikus függvénye, sőt még az sem garantálható, hogy a kritériumfüggvény konvex függvény legyen. Ilyen esetekre az előzőekben bevezetett gradiens alapú eljárásokat és az eljárások eredményét külön kell értékelnünk.
A paramétereiben nemlineáris modellek egyik legfőbb jellemzője, hogy a hibafelület nem unimodális: a hibafelületen nem csak egy – globális – szélsőérték (maximum vagy minimum) található, hanem számos – lokális – szélsőérték is lehet. Vagyis a
(2.121)
feltételt nemcsak a globális szélsőértékhez tartozó w* paramétervektor, hanem egyéb paramétervektorok is biztosíthatják. Sőt, általános esetben az is előfordulhat, hogy egy egész paramétertartományban a felület gradiense zérus, ami azt jelenti, hogy a hibafelületen valamekkora kiterjedésű „lapos” terület is található.
A gradiens alapú eljárások ilyenkor is alkalmazhatók, az eredményeket azonban külön értékelni kell. A gradiens eljárásokkal kapott eredmény nem feltétlenül jelenti a legkisebb kritériumértékhez tartozó megoldást, így az eredmény minősége – a kritériumérték – alapján mérlegelni kell, hogy a kapott megoldásvektor a hibafelület globális minimumpontját adja meg, vagy csupán egy lokális minimumpontot. A megoldást még ezen utóbbi esetben is elfogadhatjuk, ha a kapott kritériumérték az adott alkalmazást tekintve elegendően kicsi. Ha nem, akkor újabb (lokális) minimumpontot kell keresni, ami szerencsés esetben egyben a globális minimumpont is lehet.
A nemkvadratikus hibafelületek további következménye, hogy olyan eljárásoknál, ahol a konvergenciához szükséges lépések száma kvadratikus hibafelület mellett meghatározható, most ez sem lesz érvényes. A konjugált gradiens eljárásnál például nem kvadratikus hibafelület mellett N iteráció után az algoritmus nem állítható le. Ilyenkor az az általánosan javasolt eljárás, hogy N iterációnként indítsuk újra az egész algoritmust egy új kezdeti gradiens meghatározásával. Meg kell azonban jegyeznünk, hogy valóságos esetekben az N-lépéses konvergencia még kvadratikus hibafelület mellett sem biztosított, hiszen numerikus problémák miatt a gradiens értékére sohasem fogunk nullát kapni. Ilyenkor az algoritmus leállítása sem történhet meg a gradiens értéke alapján. Helyette vagy egy adott iterációszám, vagy ha az egymást követő iterációkhoz tartozó kritériumértékek különbsége megfelelően kicsi jelentheti a leállás feltételét. A tapasztalat szerint azonban a konjugált gradiens módszer még nem ideális esetben (numerikus problémák, vagy nem "teljesen" négyzetes hibafelület) és az optimumtól távol is kedvezőbb konvergenciát mutat, mint a direkt gradiens módszerek.
További gradiens-alapú módszerek
Az előzőekben láttuk, hogy egyes eljárások, mint a Newton, a Newton/LMS, de a konjugált gradiens módszer is a hibafelületről az R mátrix figyelembevétele által a gradiensen túl további információt is felhasználnak. Kvadratikus hibafelület esetén R a hibafelület második parciális deriváltjaiból képezett H ún. Hesse mátrixszal egyezik meg, tehát R valójában a hibafelület görbületéről szolgál információval. Kvadratikus hibafelületet – mint láttuk – paramétereiben lineáris modell és négyzetes hibafüggvénymellett kapunk. A hibafelületre vonatkozó járulékos információ a konvergenciasebességet jelentősen megnöveli a csupán a gradiens felhasználásával dolgozó LMS eljáráshoz képest. A Newton módszerrel pl. négyzetes hibafelület mellett akár egy lépésben is eljuthatunk a hibafelület minimumpontjába.
A Newton illetve a Newton/LMS eljárások előnyös konvergencia tulajdonságai ellenére számos nehézséget is rejtenek. Egyrészt alkalmazásukhoz kell, hogy R pozitív definit legyen, másrészt R-1 számításigényes. További gondot jelenthet, ha a hibafelület nem négyzetes. Az alábbiakban bemutatott Levenberg-Marquardt eljárás ezekre a nehézségekre igyekszik megoldást találni.
A nemkvadratikus kritériumfelület kezelhető olyan módon hogy a C(w) kritériumfüggvényt Taylor-sorának első néhány tagjával közelítjük. Ha az első és másodfokú tagokat vesszük figyelembe, akkor egy nemkvadratikus kritériumfelület kvadratikus közelítésével dolgozunk.
(2.122)
ahol
(2.123)
a kritériumfelület második parciális deriváltjaiból felépített Hesse-féle mátrix. A (2.122) összefüggésnek a (2.53) összefüggéssel való összevetéséből látszik, hogy a H mátrix az R mátrixnak feleltethető meg.
Ha a (2.122) összefüggés minimumát w szerinti deriválással keressük, akkor a közelítő négyzetes hibafelület minimumpontját egy lépésben is elérhetjük. Ehhez a
(2.124)
feltételt kell kielégítenünk, amelyből a Newton módszert (lásd (2.61)) kapjuk:
(2.125)
Az 1/2-es szorzó a korrekciós tagból most hiányzik, mert a (2.122) összefüggés jobboldalának harmadik tagjában a (2.61) összefüggéssel ellentétben
szerepel. Az így kapott eljárás nemkvadratikus hibafelület esetén nem feltétlenül jobb, mint a gradiens alapú eljárás. Ezért hatékonyabb lehet, ha a Newton eljárás és az egyszerű gradiens alapú eljárás „keverékét” alkalmazzuk. Ezt javasolja a Newton módszer Levenberg-Marquardt félemódosítása:
(2.126)
Látható, hogy a (2.126) összefüggés valójában a legmeredekebb lejtő módszer és a Newton eljárás kombinációja, ahol a kétféle eljárás arányát a λ(k) lépésfüggő együttható szabja meg. Ha λ(k) nagy, a (2.126) alapján történő súlymódosítás a legmeredekebb lejtő módszert, míg ha λ(k) kicsi, a Newton eljárást közelíti. A λ(k)I beépítése az eljárásba regularizációként is értelmezhető, ami a mátrix invertálhatóságát akkor is biztosítja, ha H közel szinguláris.
A neurális hálózatok tanításánál hatékonynak bizonyult a H mátrix egy közelítése, amely a következő gondolatmeneten alapszik. Tételezzük fel, hogy a kritériumfüggvény önmagában négyzetes, de a paraméterfüggés nemlineáris, tehát
. (2.127)
Ekkor a gradiens vektor
(2.128)
alakban írható, illetve ennek minden sorát deriválva minden paraméter szerint megkapjuk a H mátrixot:
, (2.129)
ahol a szögletes zárójelben szereplő kifejezés y(w) másodrendű parciális deriváltjainak mátrixát szimbolizálja. Mivel a (2.129) kifejezés második tagja ε-nal szorzódik, a H mátrix az optimumhoz közeledve egyre inkább az első tagtól függ, hiszen akkor általában mind ε, mind y(w) görbülete egyre kisebb, ezért felvethető a
(2.130)
közelítés. Ha H (2.130) szerinti közelítését (2.126)-ban alkalmazzuk, akkor számítási hatékonyság szempontjából kedvezőbb megoldást nyerünk, hiszen a Hesse mátrix (2.130) szerinti becslése jóval kisebb számításigényű, mintha a valódi második deriváltak alapján számítanánk. Meg kell jegyezni, hogy sok sikeres alkalmazás fűződik egy olyan megoldáshoz, ahol az I egységmátrix helyett egy olyan Ω diagonálmátrixot alkalmazunk, melynek elemei megegyeznek H (2.130) szerinti becslésének diagonális elemeivel. Az így kapott eljárást az irodalomban Levenberg-Marquardt módszernek nevezik [Mor77].
Feltételes szélsőérték-kereső eljárások
Neuronhálók, illetve egyes tanuló rendszerek konstrukciójánál az optimális paraméterkészlet meghatározása sokszor feltételes szélsőérték-keresési eljárásra vezet. Ilyen esetekkel találkozunk például, ha a leképezés hibájára vonatkozó kritérium vagy kockázat minimalizálását bizonyos mellékfeltételek teljesülése mellett kell elvégeznünk. Mint az egyes hálóarchitektúráknál látni fogjuk, ilyen mellékfeltétel lehet a háló leképezésére megfogalmazott valamilyen simasági feltétel, vagy a paraméterekre vonatkozó megkötés: a paraméterek értékei a lehető legkisebbek legyenek, vagy a paramétervektor komponenseinek összege legyen egy adott érték, tipikusan 1. A mellékfeltételek megfogalmazásának egy lehetséges módja a 2.1 részben bemutatott regularizáció is.
A feltételes szélsőérték problémák gyakran a következő formában fogalmazhatók meg: keressük egy skalár értékű konvex C(w) kritériumfüggvény extrémumához tartozó w*-ot azzal a feltétellel, hogy egyidejűleg a g(w)=0 formában adott mellékfeltétel is teljesüljön.
Az ilyen típusú feltételes szélsőérték-keresési problémák hatékony megoldására szolgál a Lagrange multiplikátoros módszer. A Lagrange multiplikátoros eljárásnál meg kell fogalmazni egy módosított kritériumfüggvényt, amely mind az eredeti kritériumfüggvényt, mind a mellékfeltételt magában foglalja:
(2.131)
A feltételes szélsőérték a
megoldásából adódik.
Amennyiben nem egyenlőség, hanem egyenlőtlenség formájában vannak mellékfeltételeink, vagy az egyenlőség típusú feltételek mellett egyenlőtlenség típusú mellékfeltételeink is vannak, a Karush-Kuhn-Tucker (KKT) elmélet alkalmazásával kaphatunk megoldást, amely elmélet a Lagrange módszer kiterjesztésének tekinthető.
Mind a Lagrange, mind a KKT elmélet rövid összefoglalását a Függelékben adjuk meg.
2.5.2. Sztochasztikus szélsőérték-kereső eljárások
A gradiens módszerek hatékony működéséhez a kritériumfelületről bizonyos tulajdonságokat fel kell tételezni. A kedvező konvergencia-sebességet általában csak kvadratikus hibafelület mellett biztosítják, továbbá a minimumhely elérése csak akkor biztos, ha a felületen nincsenek lokális minimumok (unimodális felület).
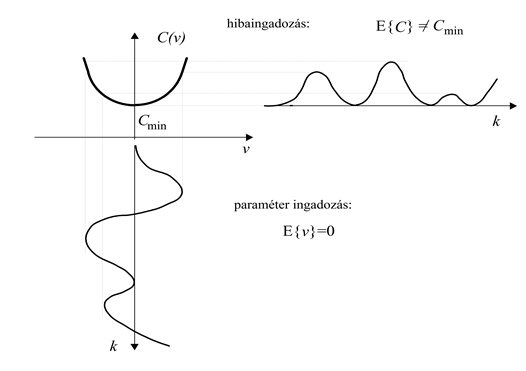
A neurális hálózatokra tipikusan a nem kvadratikus hibafelületek, a lokális minimumok fennálltának lehetősége és általában a konvergencia szempontjából kedvezőtlen tulajdonságok a jellemzőek. A lokális minimumhelyekben való bennragadás elkerülésére sztochasztikus gradiens eljárásokat dolgoztak ki, amelyek fő jellemzője, hogy a kritériumfelületen valamilyen − általában kis és az algoritmus során változó − valószínűséggel a felfelé mozgást is megengedik, lehetővé téve a lokális minimumból való kiszabadulást. A sztochasztikus gradiens eljárások célja, hogy a tanulási folyamat során véletlen zaj felhasználásával lehetővé tegyük, hogy a hálózat a lokális minimumból kikerüljön. Ennek egy egyszerű, heurisztikus módja, ha olyan esetekben, amikor a lokális minimumba kerülés gyanúja fennáll, vagyis a tanulási folyamat több lépése sem eredményez hibacsökkenést, a hálózat aktuális súlyaihoz zajt adunk. Additív zajként általában egyenletes vagy Gauss eloszlású valószínűségi változó aktuális értékeit tekintjük. A súlyoknak az ilyen véletlenszerű "megrázása" kiugrathatja a hálózatot a lokális minimumból.
A zaj felhasználás egy további lehetséges módja, ha az eddigi kritériumfüggvényt az alábbiak szerint módosítjuk:
, (2.132)
ahol
a módosított kritériumfüggvény, az
értékek az
független fehérzaj komponensei, a wi-k pedig a w súlyvektor komponensei. A c(k) lépésfüggő együttható az additív zaj amplitúdóját határozza meg; ezt olyan módon kell megválasztani, hogy a k diszkrét időindex előrehaladtával tartson nullához. Az így definiált kritériumfüggvény esetén a súlymódosítás az i-edik súlykomponens esetében:
. (2.133)
Az eljárás egyik kulcskérdése a c(k) paraméter megválasztása. Legtöbbször c(k) k monoton csökkenő függvénye, azonban néhány esetben bonyolultabb módon változtatjuk c(k)-t. Pl. c(k) értékét átmenetileg növelhetjük, ha észrevesszük, hogy lokális minimumba kerültünk. A legegyszerűbb választás az alábbi lehet:
, (2.134)
ahol β>0 és α>0. Ekkor β a kezdeti (k=0) zajamplitúdót határozza meg, míg α az additív zaj csillapodásának mértéke.
A sztochasztikus szélsőérték-kereső algoritmusok között kell megemlíteni a szimulált lehűtést (simulated annealing, SA) [Aar89] is, amely szintén megengedi, hogy a hibafelületen valamilyen valószínűséggel felfelé, a nagyobb hiba irányában is elmozduljunk. A felfelé mozgás valószínűsége a minimalizáló eljárás előrehaladtával fokozatosan csökken, mígnem a minimum közelében 0-hoz tart. A szimulált lehűtés előnye, hogy a globális minimumhoz konvergál 1 valószínűséggel, hátránya az eljárás nagyfokú lassúsága. A szimulált lehűtéssel részletesebben a 11. fejezetben foglalkozunk.
Tulajdonképpen az LMS eljárások is felfoghatók sztochasztikus gradiens módszerekként, hiszen a pillanatnyi gradiensen alapulnak, ami a valódi gradiens zajos értékének feleltethető meg. Láttuk is az LMS eljárás tárgyalásánál, hogy konstans μ mellett − még ha a μ a konvergenciát biztosító tartományon belül is van − a w* megoldásvektort nem fogjuk elérni, az eljárás nem áll le, hanem a súlyvektor w* valamekkora környezetében fog "vándorolni". Az eljárás konvergenciája csak akkor biztosítható, ha konstans μ helyett lépésenként csökkenő μ -t alkalmazunk. A lépésfüggő μ megválasztására a sztochasztikus approximáció ad támpontot. A sztochasztikus approximáció ún. Robbins-Monro-algoritmusa olyan sztochasztikus zérus-kereső módszer, amely zajos megfigyelések ellenére is biztosítja a konvergenciát (ld. még [Bat92]). A konvergencia akkor biztosítható, ha a lépésfüggő μ -re betartjuk az alábbi feltételeket:
. (2.135)
Megjegyezzük, hogy ezek a feltételek kielégíthetők pl. μ(k)=μ0/k választással (ahol μ0 alkalmasan megválasztott konstans).
Bár a felügyelt tanítású hálózatoknál többségében determinisztikus vagy sztochasztikus gradiens eljárásokatalkalmaznak, számos esetben egyéb, nem a hibafelület gradiensén alapuló eljárást használnak. A gradiens eljárások hátránya ugyanis − akár determinisztikus, akár sztochasztikus eljárásról van szó −, hogy a kritériumfelületről valamilyen a priori ismerettel kell rendelkezzünk. Az általános, nem gradiensen alapuló kereső eljárások viszont nem tételeznek fel semmit a kritériumfelületről. A keresés során valamilyen véletlen (egyes esetekben determinisztikus) algoritmus szerint feltérképezik a felületet. A legkézenfekvőbb megoldás a kritériumfelület teljes feltérképezése (a megoldási tér teljes végigtesztelése), azaz minden lehetséges paraméterérték (súlyvektor) mellett a kritériumfüggvény meghatározása. Mivel csak véges számú pontban határozható meg a kritériumfüggvény értéke, a paraméterek változtatása diszkrét lépésekben történhet. Ez azt jelenti, hogy a súlytérre egy megfelelő finomságú (nem feltétlenül egyenletes felbontású) rácsot helyezünk és a kritériumértékeket a rácspontokban határozzuk meg. Ez az ún. "kimerítő (teljes) keresés" (exhaustive search) megfelelően finom felbontás mellett biztosan megtalálja a globális minimumot.
A dimenziószám növelésével viszont a rácspontok száma hatványozottan növekszik, ezért a legegyszerűbb esetektől eltekintve − tehát szinte minden valós problémánál − az eljárás elfogadhatatlan mértékű számítást igényel. A nagy számításigény mérséklésére a determinisztikus teljes keresés helyett egyéb kereső eljárások alakultak ki, melyek a kritériumfelület feltérképezésének eltérő módját alkalmazzák. Ezen eljárások közös jellemzője, hogy a kritériumfelület feltérképezését nem előre meghatározott módon, hanem lépésről lépésre, a pillanatnyi állapottól függően végzik. A következőkben a (nem gradiens alapú) kereső eljárások két, jelentősen eltérő családjával foglalkozunk.
Véletlen kereső módszereknél a paraméterértékek véletlenszerű megváltoztatásával próbálkozunk. Ha egy próbálkozás eredményeképpen kapott paraméterhez tartozó kritériumérték az előző pontbelinél kisebb, az új pontot tekintjük a következő lépés kiinduló pontjának, ellenkező esetben a régi paraméterértéket tartjuk meg és a keresést tovább folytatjuk. A véletlen keresési eljárásoknak − a hatékonyság növelése érdekében − különböző változatait dolgozták ki. Az alábbiakban a véletlen keresés alapeljárásának és egy módosított változatának fő lépéseit foglaljuk össze.
Mátyás véletlen optimalizálási módszere [Mát65] 1 valószínűséggel biztosítja a globális minimumhoz való konvergenciát, abban az esetben, ha a keresési tér kompakt (korlátos és zárt). Jelölje W a kompakt keresési teret, w(k) pedig a keresési tér egy pontját.
A módszer a következő lépésekből áll:
-
válasszunk egy kezdeti pontot: k=0,
2.
12. ,
-
generáljunk egy nulla várható értékű, Gauss véletlen vektort:
15.
25. , módosítsuk a véletlen vektorral a pillanatnyi pont értékét:
27.
39. és ha
41.
53. , ugorjunk a 3. lépésre, egyébként ugorjunk a 4. lépésre,
-
ha
56.
70. <
72.
84. , akkor legyen
86.
102. , vagyis a módosított pontot (paraméterértéket) tekintsük a megoldás következő közelítésének,
ha
•
• , akkor a paraméterértéket ne változtassuk meg, tehát w(k+1)=w(k) maradjon,
-
növeljük meg k értékét: k=k+1 és folytassuk az eljárást a 2. lépéssel.
A konvergencia gyorsítható, ha a 3. lépést az alábbival helyettesítjük:
-
ha
4.
18. <
20.
32. , akkor
34.
50. és
legyen,
ha
és
<
, akkor:
és
legyen,
egyébként pedig
,
ahol m(k) a Gauss valószínűségi vektorváltozó várható értéke a k-adik lépésben.
A módosított eljárás tehát változó várható értékű Gauss véletlen vektort használ. Kezdetben a várható érték itt is nulla: m(0)=0. Bizonyítható [Sol81], hogy a módosított eljárás is 1 valószínűséggel konvergens és a globális minimumhoz konvergál, ha a keresési tér kompakt.
Neurális hálózatokra való alkalmazásnál általában nem biztosítható, hogy a keresési tér kompakt legyen. A súlyértékek nem szükségszerűen korlátos tartományban vehetnek fel csak értékeket. Ez azt jelenti, hogy a véletlen keresési módszerek nem feltétlenül konvergálnak a globális minimumhoz. Abban az esetben azonban, ha a keresési teret korlátozzuk, akkor e tartományon belül a globális minimumhoz való 1 valószínűségű konvergencia igaz. E nehézség ellenére, alkalmazástól függően a véletlen keresési módszerekkel más eljárásoknál gyorsabb konvergencia is elérhető.
A véletlen keresési módszerek sok esetben sikerrel alkalmazhatók egyéb szélsőérték-kereső eljárásokkal, pl. gradiens alapú módszerekkel kombinálva. Ilyenkor a gradiens módszert alkalmazzuk mindaddig, amíg a kritériumfüggvény értékének csökkenése egy adott korlátnál kisebb nem lesz, majd áttérünk a véletlen keresésre. A kritériumcsökkenés lelassulása vagy megállása annak jele, hogy a hibafelület meredeksége nagyon lecsökkent, esetleg lokális minimumhelyet értünk el. A minimumhelyben való bennragadás elkerülésére alkalmazzuk most a véletlen keresést, mindaddig, amíg a hibafelületen meredekebb részre nem érünk ismét, ahol célszerűen visszatérünk a gradiens alapú módszerre.
A genetikus algoritmusok [Hol75], [Gol89a] az evolúció számítógépes modelljei, a természetes szelekciót utánozzák. Az evolúció a természetes kiválasztódással központi szerepet tölt be a biológiában. A mesterséges intelligencia témakörében, a mesterséges intelligens rendszerek létrehozásánál az utóbbi időben egyre gyakrabban alkalmazzák a természetes kiválasztódás modelljét.
A genetikus algoritmusok sztochasztikus keresési algoritmusoknak tekinthetők, ahol a paramétertér feltérképezése és az iterációnként egyre jobb megoldások előállítása az eddigi eljárásoktól gyökeresen eltérő módon történik. Az eddigi szélsőérték-keresési eljárások − akár a gradiens módszerek, akár a véletlen keresés − a paramétertérben egy pontot mozgattak és a pont minden egyes állapotában − ami egy lehetséges megoldásnak felelt meg − kiértékelték a kritériumfüggvényt, majd ennek eredményétől függően folytatták az eljárást. Az alapvető eltérés e két módszer között csak az egymást követő pontok meghatározásában volt.
A genetikus algoritmusok ezzel szemben nem különálló pontokban vizsgálják a kritériumfelületet, hanem egyszerre több ponton értékelik ki, tehát egy lépésben a megoldások egész halmazával dolgoznak. Genetikus algoritmusoknál a megoldások egy adott lépésben érvényes halmazát populációnak nevezik. A populáció elemei különböző sikerrel oldják meg a feladatot, ami szélsőérték-keresésnél azt jelenti, hogy a populáció elemei a kritériumfüggvény különböző pontjait határozzák meg. E pontok között lesznek olyanok, amelyek a globális minimumhoz közelebb esnek − ahol a kritériumfüggvény értéke kisebb −, és lesznek a megoldástól távolabb eső pontok is. A populáció elemei tehát a feladat szempontjából eltérő tulajdonságúak, képességűek. A genetikus algoritmusoktól azt várjuk, hogy a természetes szelekció mintájára egy látszólag spontán fejlődés során egy adott populációból olyan újabb populációt, ill. olyan újabb és újabb populációkat hozzanak létre, amelyekben a jó megoldáshoz közeli megoldások egyre nagyobb számban lesznek megtalálhatók, és amelyekben a gyenge eredményt szolgáltató elemek egyre ritkulnak. Ez azt jelenti, hogy valójában a genetikus algoritmusok is egy hálót helyeznek a kritériumfelületre, azonban e háló nem rögzített felbontású, hanem lépésenként változik. Ezen túl a kritériumfüggvény kiértékelése a háló rácspontjaiban nem egyenként történik, hanem minden egyes lépésben a lépéshez tartozó háló összes rácspontjában. A kiértékelés eredményeképpen egy új háló jön létre, amelynek lehetnek közös rácspontjai az előző hálóval, de alapvető jellemzője, hogy miközben egyes régi rácspontok eltűnnek, új rácspontokkal is fog rendelkezni, és ezen rácspontok a kritériumfüggvény kedvezőbb tartományain sűrűsödnek: a rácspontok sűrűsége arányos lesz az adott tartomány jóságával. Bizonyos szempontból tehát a genetikus algoritmus a véletlen kereséssel rokonítható, hiszen itt is a teljes keresési tér valamilyen feltérképezéséről van szó. A genetikus algoritmus azonban − szemben a véletlen kereséssel − nem vakon keres. A keresés az egymást követő lépésekben egyre inkább a kritériumfüggvény minimumhelyei környezetére koncentrálódik.
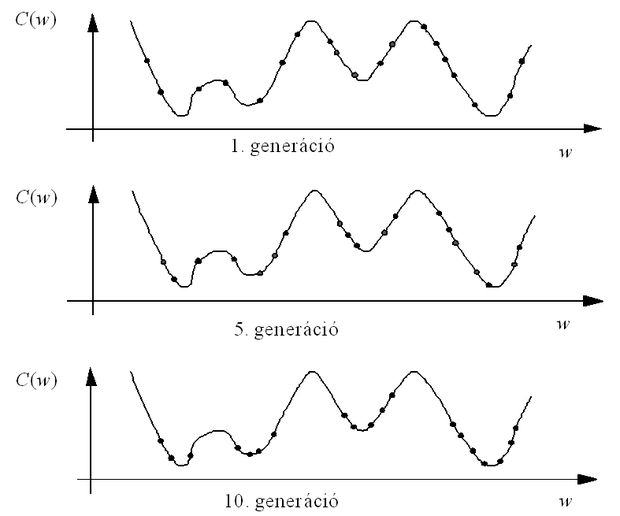
Az egymást követő populációkat − biológiai mintára − generációknak nevezzük, tehát az algoritmus az egymást követő generációk során egyre jobb megoldás-halmazokat állít elő. E folyamat követhető a 2.16 ábrán. Az egydimenziós paramétertérben az egyre későbbi generációk során a populáció jobb megoldást adó elemei a kritériumfüggvény minimumhelyei közelében sűrűsödnek.
Egy populáció elemeinek tulajdonságait valamilyen módon reprezentálni kell. E reprezentáció – megint csak biológiai szóhasználattal élve – kromoszómákkal történik, amely jelen esetben olyan bitfüzéreket – stringeket – jelent, amelyekben minden egyes bit egy tulajdonságot reprezentál. Ha a string egy adott pozícióján 1 található, az adott elem a kérdéses tulajdonsággal rendelkezik, míg a 0 érték e tulajdonság hiányát jelenti. A megoldások egy populációja tehát a kromoszómák, bináris stringek egy populációját jelenti, és az algoritmus lényegében az egymást követő string-populációk fejlődése során jut el a megfelelő megoldásig. A megoldási tér (paraméter tér) minden egyes pontjának egy kromoszóma felel meg.
Az eddigiek alapján összefoglalhatjuk a genetikus algoritmusok fő jellemzőit:
-
a paraméterek optimalizálása során nem az egyes paramétereket próbálja megtalálni, hanem az egész paraméterkészlettel (általában annak bináris kódolású változatával) dolgozik egyszerre,
-
a keresés során nem egyetlen – az optimális – paramétert keresi, hanem a megoldások egész halmazát adja meg; ezek mindegyike jó megoldás a kritériumfüggvény szempontjából, bár nem egyformán jók,
-
csak a kritériumfüggvény egyes értékeit használja, de a kritériumfüggvényről semmit sem tételez fel (pl. unimodalitás, folytonosság, differenciálhatóság), hiszen nem alkalmaz deriválást (a véletlen keresés módszerre hasonlít ebből a szempontból is),
-
valószínűségi átmenetekkel dolgozik.
Hogy az egymást követő populációk egyre jobb tulajdonságú stringeket tartalmazzanak, a stringek valamilyen kiértékelésére van szükség. Minden stringhez hozzárendelhetünk egy "jóság" (fitness) értéket, ami lényegében annak mértéke, hogy egy adott string által képviselt megoldás milyen kritériumfüggvény-értéket eredményez. Minél kisebb a kritériumfüggvény-érték, annál jobb a megoldás, tehát a fitness érték annál nagyobb.
A genetikus algoritmus a kromoszómák generációival dolgozik. A megfelelő működést az jelenti, ha az újabb generációk átlagos jósága (fitness-értéke) egyre nagyobb, de legalábbis nem csökken. Tehát az egyes lépések során a jó kromoszómák által hordozott információt kell tovább örökíteni a következő generációra.
A generációk közötti átmenet valószínűségi operátorokkal történik. A legegyszerűbb genetikus algoritmus a következő alap-operátorokkal rendelkezik:
A reprodukció (reproduction) az a folyamat, amikor egy string a következő generáció részeként is megjelenik, vagyis egy megoldás a következő generáció megoldás-halmazának is része marad. Egy adott stringnél a reprodukció, vagyis a túlélés bekövetkezésének valószínűsége a string jóságával van kapcsolatban. Minél nagyobb egy kromoszóma jósága az egy populációba tartozó kromoszómák átlagos jóságához viszonyítva, annál nagyobb számban fog reprodukálódni a kromoszóma, vagyis annál nagyobb számban fog előfordulni a következő generációban. A reprodukciónak ezt a módját arányos kiválasztási mechanizmusnak nevezzük.
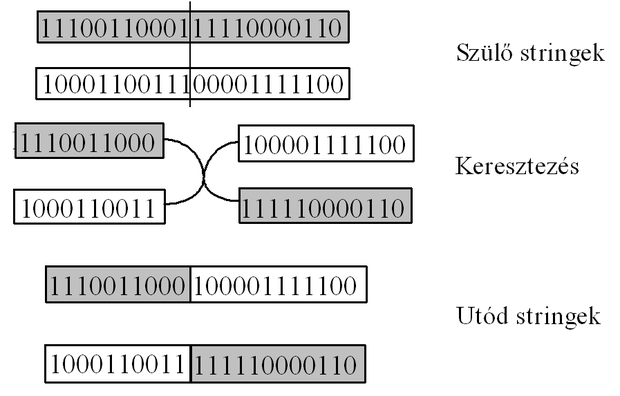
A keresztezésnél (crossover) egy generáció két kromoszómája – a szülő kromoszómák – a tulajdonságaik keresztezése révén hoznak létre új tulajdonságú utódokat. Ilyenkor a szülők bitmintái kereszteződnek új bitkombinációkat hozva létre. Az utódok bitkombinációi részben az egyik szülő, részben a másik szülő bitkombinációit fogják tartalmazni. A keresztezés operátor legegyszerűbb formája az ún. egypontos keresztezés, amikor az adott generáció bitfüzérei páronként úgy hoznak létre utódokat, hogy egy bitfüzér-pár mindkét tagja egy véletlenszerűen kiválasztott pontnál szétválik, és az így létrejövő részstringek keresztbe kapcsolódva hoznak létre új stringeket. A folyamatot a 2.17 ábrán követhetjük. Megjegyezzük, hogy a szülő kromoszómákból az utód kromoszómák létrehozásánál a keresztezés a legegyszerűbb operáció. Bár a természetben nem található erre minta, genetikus algoritmusoknál a szülő kromoszómák komplex összekeverése is lehetséges. Ezen komplex operációkat rekombinációnak hívják, amelyek egy speciális, egyszerű esete a keresztezés [Rad93].
A mutáció (mutation) során egy string egy bitje véletlenszerűen, általában igen kis valószínűséggel megváltozik. A mutáció következtében teljesen új bitkombinációk jöhetnek létre, így megakadályozhatják a további, fejlődésre képtelen, egyöntetű populáció létrejöttét. Az új bitkombinációk a megoldási tér olyan területeit is feltérképezhetik, amelyekre az eddigi populációk nem terjedtek ki.
Fentiek alapján az algoritmus a következő lépésekből áll:
-
egy kromoszóma populáció véletlen generálása,
-
a populáció minden kromoszómájának kiértékelése (a fitness értékek meghatározása),
-
új kromoszómák létrehozása a fenti három operátorral,
-
az új kromoszómák kiértékelése,
-
az új populáció (a következő generáció) létrehozása azáltal, hogy a régi kromoszómák közül a leggyengébbeket az újak közül a legjobbakkal váltjuk fel,
-
leállás: ha az eredmény elég jó, nem folytatjuk az eljárást.
A három operátor hatását az alábbi egyszerű példán követhetjük.
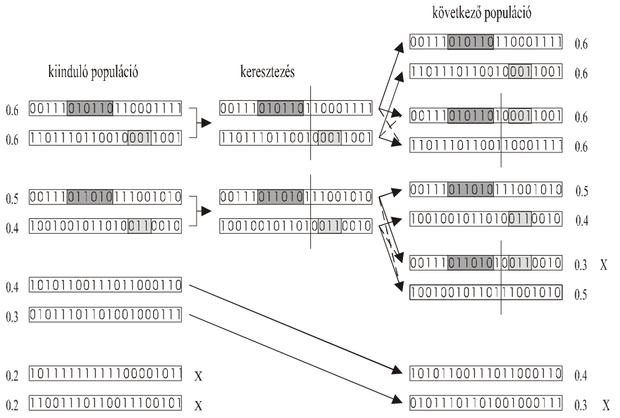
2.4 Példa
Tekintsünk egy 4 kromoszómából álló populációt, melyben az egyes kromoszómák (
) 10 bitesek. Legyen az egyes bitstringek jósága (
) rendre 0,9; 0,6; 0,6 és 0,3. Ekkor a populáció átlagos jósága
= 0,6 az egyes kromoszómák jóságainak az átlagos jósághoz viszonyított értékei (
) pedig rendre 1,5; 1,0; 1,0 és 0,5-re adódnak. Ha a kiválasztás ezen értékekkel arányos valószínűség szerint történik, akkor az egyes stringek reprodukciójának valószínűségei (
, n=4) 0,375; 0,25; 0,25 és 0,125.
A szelekció – arányos kiválasztási mechanizmust alkalmazva – ezek után a következőképpen zajlik. Határozzuk meg az egyes kromoszómák relatív jóságait – a
értékeket – a populációt jellemző összeg-jósághoz viszonyítva. Osszuk fel a [0,1] intervallumot ezen relatív jóságoknak megfelelő intervallumokra. Generáljunk a [0,1] intervallumban egyenletes eloszlású véletlen számokat és attól függően reprodukáljuk az egyes kromoszómákat, hogy a véletlen szám a [0,1] intervallum mely részintervallumába esik.
Mivel a részintervallum-hosszak arányosak az egyes kromoszómák relatív jóságával, a reprodukció valószínűsége is arányos lesz ezekkel az értékekkel, vagyis az arányos kiválasztási mechanizmust valósítottuk meg és az egyes kromoszómák
-vel arányos számban reprodukálódnak. A szelekciót követően a kromoszómák átlagos jósága növekedett:
=0,75.
A kromoszómák alakulását az egyes operátorok alkalmazása után a 2.1 táblázat mutatja. Ugyancsak a táblázatból látható a keresztezés (egypontos: az ötödik és a hatodik bit között) és a mutáció hatása. A táblázatból az is látható, hogy a keresztezés hatására az eddigieknél jobb képességű egyed (P3: f1=1) keletkezhet, de az is, hogy a keresztezés a populáció átlagos jóságának stagnálását, a mutáció pedig az átlagos jóság stagnálását ill. csökkenését is eredményezheti (
=0,75 ill.
=0,6).
A genetikus algoritmusok valódi teljesítőképessége jobban megérthető, ha bevezetjük a szkéma vagy hasonló mintázat fogalmát [Hol75]. Ha két vagy több string hasonló képességekkel rendelkezik, akkor a stringek egy vagy több pozíciójában egyezés található. A stringek közötti lényeges hasonlóságok kezelésére vezethető be a hasonló mintázat vagy szkéma elnevezés, amely egy olyan részstringet jelöl, amelyben a 0 és 1 értékű biteken kívül don't care, közömbös bitek is lehetnek. Pl. a 8 hosszúságú 1*0*01** szkéma mindazon stringeket képviselni fogja, amelyekben 1 található az első és a hatodik pozícióban, 0 a harmadikban és az ötödikben. A szkémák hossza megegyezhet a string hosszával, de legtöbbször annál kisebb. A szkéma fogalmának bevezetésével lehetőség nyílik annak bemutatására, hogy generációról generációra a jó tulajdonságú stringek száma – vagyis azon stringek száma, amelyekben jó tulajdonságú szkéma található – az egyes populációkban hogyan növekszik.
2.1. táblázat - A kromoszómák alakulása az egyes operációk után
|
Kromoszóma
|
Jóság
|
Populáció
|
|
1 1 1 1 1 1 1 0 1 1
0 1 1 0 1 0 1 0 1 1
1 0 0 0 0 1 1 1 1 1
0 0 0 0 0 1 1 1 0 0
|
0,9
0,6
0,6
0,3
|
Kiinduló (P1)
|
|
1 1 1 1 1 1 1 0 1 1
1 1 1 1 1 1 1 0 1 1
0 1 1 0 1 0 1 0 1 1
1 0 0 0 0 1 1 1 1 1
|
0,9
0,9
0,6
0,6
|
Szelekció után (P2)
|
|
1 1 1 1 1|1 1 1 1 1
1 1 1 1 1 1 1 0 1 1
0 1 1 0 1 0 1 0 1 1
1 0 0 0 0|1 1 0 1 1
|
1,0
0,9
0,6
0,5
|
Keresztezés után (P3)
|
|
0 1 1 1 1 1 1 0 1 1
1 1 1 1 1 1 1 0 1 1
0 1 1 0 1 1 1 0 1 1
1 0 0 0 0 1 1 0 1 1
|
0,9
0,6
0,6
0,3
|
Mutáció után (P4)
|
Vizsgáljuk meg, hogyan hatnak az egyes operátorok egy S szkéma előfordulási gyakoriságára a generációk függvényében. Ehhez vezessük be a következő jelöléseket: jelölje m(S,k) azon stringek számát, amelyek a k-adik generációban tartalmazzák az S szkémát, o(S) a szkéma rendjét (order), ami a szkémán belüli rögzített értékű bitek száma és
a szkéma meghatározó hosszát (definitive length), ami az első és utolsó rögzített bit pozíciói közötti távolság. Pl. az előző szkéma (1*0*01**) estében o(S)=4, δ(S) =5. A reprodukció során egy kromoszóma annál nagyobb valószínűséggel kerül kiválasztásra, minél nagyobb az adott kromoszóma jósága az egész populáció kromoszómáinak átlagos jóságához viszonyítva.
Ha
az i-edik kromoszóma jóságát jelöli, a reprodukció során egy stringet (kromoszómát)
(2.136)
valószínűséggel választunk ki. Ekkora valószínűséggel lesz tehát az i-edik kromoszóma eleme a következő generációnak. Ha kiválasztunk n kromoszómát a régi populációból, akkor az n elemű új populációban egy S szkémát tartalmazó stringek számát a következő összefüggés adja meg:
(2.137)
mivel
az n elemű új populáció átlagos jósága. Itt f(S) az S szkéma
jóságát, vagyis azon stringek átlagos jóságát jelöli, melyekben az S szkéma megtalálható. Ez azt jelenti, hogy azok a szkémák, amelyek jósága nagyobb, mint a populáció átlagos jósága, az új generáció kromoszómáiban növekvő számban lesznek megtalálhatók, míg az átlagosnál gyengébb képességű szkémák jelenléte az új generációban csökken. Ha f(S)=(1+c)
, ahol c konstans, akkor k generációt követően az S szkémát tartalmazó kromoszómák száma:
m(S, k)=m(S,0)
, (2.138)
vagyis a szkémák túlélése a generációk függvényében exponenciálisan nő (c>0) vagy csökken (c<0).
A szkémák előfordulási gyakoriságát befolyásolja a további két operátor is. Mind a kereszteződés, mind a mutáció következtében egy szkémát alkotó bitstring megváltozhat, a szkéma széteshet, aminek következtében egyes kromoszómákból az addig meglévő szkéma eltűnik. Egy szkéma túléli a kereszteződést, ha a kereszteződési pont kívül esik a szkéma bitcsoportján. Ha l a kromoszóma hossza és
a keresztezés bekövetkezésének valószínűsége, az egypontos keresztezésnél a túlélési valószínűség :
. (2.139)
A mutáció is elronthat egy szkémát azáltal, hogy a szkéma egy rögzített bitjét megváltoztatja. Ha
egy bit véletlen megváltozásának valószínűsége, akkor a túlélési valószínűség:
(2.140)
mivel
<<1.
Feltételezve, hogy a keresztezés és a mutáció azon hatása, hogy egy szkémát elrontanak egymástól független, valamint elhanyagolva a
–t tartalmazó tagot, a három alap-operátor hatását figyelembe véve egy adott S szkéma előfordulása a következő generációban az alábbi összefüggéssel adható meg:
. (2.141)
A (2.141) összefüggést, ami Holland szkéma elméletének eredménye, a genetikus algoritmus alaptételének nevezzük.
A mutáció, illetve a keresztezés hatására azon szkémák esnek szét nagyobb valószínűséggel, amelyek rendje, illetve meghatározó hosszúsága nagyobb. Ha egy szkémát tartalmazó kromoszóma jósága az átlag jóságnál nagyobb és a szkéma rövid, továbbá, ha szkéma rendje is kicsi, akkor a szkémát tartalmazó kromoszómák száma a generációk függvényében közel exponenciálisan nő.
A reprodukció és a keresztezés operátorok hatása az evolúció során a 2.18 ábrán követhető. Az ábrán eltérő árnyalatú bitcsoportok jelölik a szkémákat. Az egyes bitsorozatok mellé írt értékek a stringek jóságát jelentik. A legkevésbé megfelelő stringek – amelyek jósága a legkisebb – nem kerülnek át a következő generációba; az ábrán X jelöli ezen kromoszómákat. Az ábra azt is illusztrálja, hogy egy stringen belül több szkéma is előfordulhat. Ha több, kedvező tulajdonságokat reprezentáló szkéma a keresztezés hatására egy utód stringben együtt jelenik meg, lehetséges, hogy a keresztezés hatására a szülő stringeknél nagyobb jóságú utód jön létre.
A genetikus algoritmusok alkalmazása különösen ott célszerű, ahol a keresési tér nagy, komplex és kevéssé ismert, illetve, ahol a kritériumfüggvény jellege olyan, hogy más, pl. gradiens alapú eljárások nem alkalmazhatók. A keresési tér mérete ugyanakkor befolyásolja a genetikus algoritmus számításigényét, hiszen nyilvánvaló, hogy nagyobb keresési tér több elemű populációt igényel.
Tipikus feladatoknál a populáció elemszáma néhányszor tíztől több ezerig is terjedhet. A viszonylag nagy elemszám számos területen gátja a genetikus algoritmusok alkalmazásának. A populáció elemszámának meghatározásán túl fontos kérdés az algoritmus egyéb paramétereinek megválasztása. Ilyen további paraméterek pl. a keresztezés típusa (egypontos vagy többpontos keresztezés) és valószínűsége
, a mutáció valószínűsége
, stb. A paraméterek megválasztására általános eredmények jelenleg nincsenek. A paraméterválasztás alkalmazástól függően, tapasztalati úton történik. Ugyancsak alkalmazástól függ, hogy hogyan képezzük le egy adott problémánál a feladat paramétereit számfüzérekké, kromoszómákká.
Fontos kérdés még az algoritmus leállítása. A leállítás megtörténhet adott számú generáció után, illetve, ha az eredmény már elég jó, vagyis az utolsó generáció kromoszómáinak átlagos jósága egy adott értéknél nagyobb. Az algoritmust azonban le kell állítani akkor is, ha egy populáció stringjei nagymértékű hasonlóságot, homogenitást mutatnak. Ebben az esetben – függetlenül a populáció átlagos jóságától – a kromoszómák jósága a további generációk során már nem fog javulni, az algoritmus megreked.
A túl korai konvergenciát eredményező egyöntetű populáció kialakulásának esélyét a reprodukció előbb említett módja – vagyis amikor egy kromoszóma továbbélése annak jóságával arányos – növeli. Ennek megakadályozására számos módosított eljárást dolgoztak ki, melyek közös jellemzője, hogy nagyobb esélyt adnak a rossz stringek továbbélésének. E módszerek részletes ismertetésére itt nincs módunk, az érdeklődő olvasó a részleteket az irodalomban pl. [Gre87], [Gal89], [Mon89] megtalálja.
Feladatok
2.1 Mutassa meg, hogy az N-dimenziós térben a lineáris szeparáló függvények VC-dimenziója h=N+1.
2.2 Adjon szemléletes példát, amely azt mutatja, hogy az
, a>0 függvények VC-dimenziója végtelen.
2.3 Tekintsük a négyszögletes indikátorfüggvények osztályát, ahol egy indikátorfüggvényt a következőképpen definiálunk:
ahol c egy középpont-vektor, d pedig a koordináta tengelyekkel párhuzamos elhelyezkedésű négyszög szélességvektora. Mutassa meg, hogy ennek a függvényosztálynak a VC-dimenziója h=2N.
2.4 Mutassa meg, hogy a legmeredekebb lejtő módszerrel dolgozó szélsőérték-kereső eljárás konvergens, ha
. Van-e a konvergenciasebesség szempontjából optimális μ? Ha igen, határozza meg.
2.5 Az LMS eljárás a pillanatnyi gradiens alapján dolgozik. Mutassa meg, hogy az LMS eljárás eredménye torzítatlan becslése a legmeredekebb lejtő eljárással kapott eredménynek, vagyis a súlyvektor várható értéke a Wiener-Hopf megoldáshoz tart.
2.6 Az LMS eljárásnál a bemenet autokorrelációs mátrixa a következő:
Határozza meg a tanulási tényező, μ konvergenciatartományát.
2.7 A következő regularizált kritériumfüggvényt alkalmazza:
ahol d(k) a kívánt válasz és y(k) a kimenet a k-adik tanítópontra k=1,…, P. Határozza meg a pillanatnyi gradiens alapú tanítási összefüggést, ha egy y=sgm(wTx) kapcsolatot megvalósító rendszer paramétervektorát kell tanítania.
2.8 Hogyan befolyásolja az LMS eljárás konvergencia-sebességét a
arány, ha
a bemeneti jel autokorrelációs mátrixának legnagyobb illetve legkisebb sajátértéke?
2.9 Milyen esetben és hogyan alkalmazható a Karhunen-Loève transzformáció az LMS eljárás konvergencia-sebességének növelésére?
2.10 A genetikus algoritmus alaptétele ((2.141) egyenlet) megadja az S szkémát tartalmazó kromószómák számának alakulását a generációk függvényében. Az összefüggés arányos kiválasztási mechanizmust alkalmazó reprodukció mellett származtatható. Definiáljon más kiválasztási mechanizmust és határozza meg a megfelelő módosított alaptételt.
2.11 Genetikus algoritmus szimulációjával határozza meg az
függvény maximális értékét, ha
.