Az ERM elv szerint a kockázat minimalizálása elérhető a tapasztalati kockázat minimalizálása alapján. Az ERM konzisztenciája azt jelenti, hogy a tapasztalati kockázat tart a valódi kockázathoz, ha a mintapontok számát minden határon túl növeljük, tehát az ERM konzisztenciájára vonatkozó elméleti eredmények a tapasztalati hiba aszimptotikus alakulására vonatkoznak és megadják a tapasztalati hiba konvergenciájának szükséges és elégséges feltételét.

Felmerül a kérdés, hogy mi szükség van egy aszimptotikus elméletre, amikor véges számú minta alapján dolgozó tanuló algoritmusokat vizsgálunk. A konzisztencia elmélet szükségességét az támasztja alá, hogy ez az elmélet a tapasztalati hiba minimalizálás konzisztenciájának nemcsak szükséges, de elégséges feltételeit is megadja. Ezért az ERM elv konzisztenciájára vonatkozó bármely elméletnek ki kell elégítenie ezeket a feltételeket.

A probléma megfogalmazásához induljunk ki az eddigi jelölésekből. Jelöljön most is $z=\text{(}x,d\text{)}$ egy tanító be-kimeneti mintapárt. A tanítási feladat során rendelkezésünkre áll egy $z_1,z_2\mathrm{,...,}{z}_l$ tanítókészlet, melynek elemeiről feltételezzük, hogy egymástól független, azonos − de ismeretlen − eloszlású mintapontok. A p(z) sűrűségfüggvényt tehát nem ismerjük. Adott továbbá egy veszteségfüggvény, $L\text{(}z,w\text{)}$ , $w\in W$ , és a cél a (2.7)-ben definiált $R\text{(}w\text{)}$ kockázat minimumát biztosító $w_0$ paramétervektor meghatározása. Mivel a mintapontok eloszlását nem ismerjük, $R\text{(}w\text{)}$ -t sem tudjuk meghatározni, így a valódi kockázat minimumát biztosító $w_0$ paramétervektort sem. Az ERM elv szerint a valódi (ismeretlen) kockázat helyett a (meghatározható) $R_{\text{emp}}\text{(}w\text{)}$ tapasztalati kockázattal dolgozunk és az ennek minimumát biztosító $w^{\ast }$ paramétervektort keressük.

A tanuló eljárások többségénél ezt az eljárást követjük anélkül, hogy az eljárás elméleti megalapozottsága bizonyított lenne. Ez ugyan természetesen adódó megoldás, hiszen a mintapontok eloszlásának ismerete nélkül csak a tapasztalati hiba határozható meg, azonban az eljárás alkalmazhatóságához a matematikai igazolás is szükséges lenne. Az igazolás és a megfelelő feltételek meghatározása ezért mind elméleti, mind gyakorlati szempontból kiemelten fontos.

Az ERM elv alkalmazhatóságához azt kell belátni, hogy az ERM elv alapján kapott becslés, $w^{\ast }$ a valódi paramétervektorhoz konvergál, ha a tanítópontok számát növeljük. A statisztikus tanuláselmélet fő eredménye éppen az, hogy megadja az ERM konzisztenciájának feltételét.

Először nézzük, hogy mit is jelent az ERM elv konzisztenciája. Jelölje $R_{\text{emp}}\text{(}{w}^{\ast }|l\text{)}$ az l mintapont alapján meghatározott tapasztalati hiba optimumát, és $R\text{(}{w}^{\ast }|l\text{)}$ azt az ismeretlen valódi kockázatot, melyet ugyancsak az l tanítópont alapján számított tapasztalati hiba minimumát biztosító $w^{\ast }$ mellett kapnánk. Az ERM elv akkor konzisztens, vagyis az ERM elv alapján számított kockázat becslés akkor konzisztens, ha mind a tapasztalati kockázat, $R_{\text{emp}}\text{(}{w}^{\ast }|l\text{)}$ , mind a valódi kockázat, $R\text{(}{w}^{\ast }|l\text{)}$ ugyanahhoz az $R\text{(}{w}_0\text{)}={\text{min}}_{w}R\text{(}w\text{)}$ határértékhez tart, ha l→∞. Vagyis

$\begin{array}{l}R\text{(}{w}^{\ast }|l\text{)}\to R\text{(}{w}_0\text{)}\text{, }\text{ha}l\to \infty \\ R_{\text{emp}}\text{(}{w}^{\ast }|l\text{)}\to R\text{(}{w}_0\text{)}\text{, }\text{ha}l\to \infty \end{array}$ (2.17)

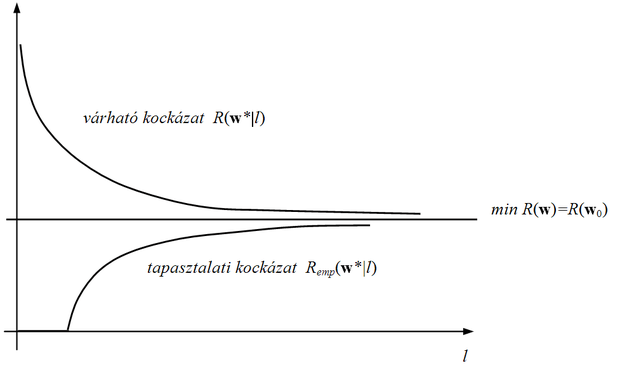
A konzisztenciát szemléletesen a 2.5 ábra illusztrálja. Amint az ábra mutatja, feltételezhető, hogy $R_{\text{emp}}\text{(}{w}^{\ast }|l\text{)}<R\text{(}{w}^{\ast }|l\text{)}$ , hiszen a tanuló eljárás a tapasztalati hiba és nem a valódi hiba minimalizálása útján határozza meg $w^{\ast }$ -ot. Intuitív módon azt várjuk, hogy l → ∞ esetén a tapasztalati kockázat bármely $w$ mellett konvergál az ugyanahhoz a $w$ paramétervektorhoz tartozó valódi kockázathoz. Ebből azonban még nem következik, hogy a tapasztalati hibát minimalizáló paramétervektor a valódi hibát is minimalizálni fogja, ha l → ∞. Hiszen a tapasztalati hiba mindig egy adott l elemű mintapontkészlet alapján határozható meg, így óhatatlanul az épp rendelkezésre álló mintakészlethez igazodó megoldást biztosít. A valódi kockázat viszont nem függ az aktuális mintakészlettől.

A statisztikus tanuláselmélet fő tételét Vladimir Vapnik és Alekszej Cservonyenkisz fogalmazták meg.

2.1 tétel [Vap91]

Adott korlátos veszteségfüggvény mellett az ERM elv akkor és csak akkor konzisztens, ha a tapasztalati kockázat egyenletesen konvergál a valódi kockázathoz a következő értelemben:

$\underset{l\to \infty }{\text{lim}}P\left\{\underset{w\in \text{W}}{\text{sup}}\left|R\text{(}w\text{)}-R_{\text{emp}}\text{(}w\text{)}\right|>\epsilon \right\}=0\forall \epsilon >0$ (2.18)

Itt P a valószínűséget, $R_{\text{emp}}\text{(}w\text{)}$ az l mintapont alapján számított tapasztalati kockázatot, $R\text{(}w\text{)}$ pedig a valódi kockázatot jelöli azonos w mellett.

Látni kell, hogy a konzisztenciatétel legrosszabb esetre vonatkozó, ún. worst case tétel, vagyis ha a konzisztencia biztosított, a fenti összefüggésnek fenn kell állnia bármely, a tanuló rendszer által megvalósított függvény (bármely $w\in W$ ) mellett még akkor is, ha az adott függvény mellett a tapasztalati és a valódi kockázat eltérése a legnagyobb.

A fenti konzisztenciatétel ugyanakkor gyakorlati felhasználásra nem alkalmas. Egyrészt nem konstruktív, vagyis ennek alapján nem tudunk a gyakorlatban tanuló rendszert konstruálni, másrészt a konvergencia ténye önmagában nem elegendő, hiszen a tapasztalati kockázat tetszőlegesen lassan is konvergálhat a valódi kockázathoz. A konvergencia-sebességről is kellene valamit állítani; meg kellene fogalmazni azon feltételeket, melyek mellett a konvergencia gyors.

Az aszimptotikus konvergenciát gyorsnak nevezzük, ha tetszőleges l > l₀ esetére teljesül a következő egyenlőtlenség:

$P\left\{\left(R\text{(}{w}^{\ast }|l\text{)}-R\text{(}{w}_0\text{)}\right)>\epsilon \right\}<e^{-cl{\epsilon }^2}$ , (2.19)

ahol c>0 egy konstans.

A statisztikus tanuláselmélet megadja mind a konzisztencia szükséges és elégséges feltételét, mind a gyors konvergencia elégséges feltételét. A feltétel megfogalmazásához néhány további fogalom bevezetésére van szükség. Az elmélet bevezet egy új entrópia fogalmat: egy függvényhalmaz entrópiájának a fogalmát és egy ún. növekedés függvényt (growth function), végül ehhez kapcsolódóan az ún. VC-dimenzió (VC-dimension) fogalmát. A függvényhalmaz entrópiájának bevezetése viszonylag természetes módon osztályozós esetre lehetséges, bár e fogalmat kiterjesztették valós értékű függvényekre is. Osztályozós esetben a veszteségfüggvény csak két értéket, nullát vagy egyet vehet fel. Az ilyen függvényeket indikátorfüggvényeknek nevezzük. A valós értékű függvényekre való kiterjesztés alapján az eredmények általánosíthatók regressziós feladatokra is; a kiterjesztéssel azonban itt nem foglakozunk.

Tekintsük az $L\left(z,w\right),w\in W$ indikátorfügvények egy osztályát és legyen adott egy $Z_l=\left\{z_i,i=\mathrm{1,...,}l\right\}$ mintakészlet. Minden egyes indikátorfüggvény két részhalmazra particionálja a mintakészletet. A particionálás kétosztályos osztályozást jelent, vagyis azt is mondhatjuk, hogy a particionálásnál a mintakészlet pontjait két eltérő színnel kiszínezzük. A függvényhalmaznak az adott mintakészletre vonatkozó sokféleségét (diversity) jelöljük N(Z_l)-vel. N(Z_l) egy olyan szám, ami azt adja meg, hogy az adott függvényosztály elemeivel az adott mintakészletet hányféle eltérő módon tudjuk kiszínezni. A függvényosztály véletlen entrópiájának (random entropy) e szám logaritmusát nevezzük:

$H\text{(}{Z}_l\text{)}=\text{ln }N\text{(}{Z}_l\text{)}$ . (2.20)

A kapott mennyiség egy valószínűségi változó, hiszen függ a Z_l mintakészlettől. A véletlen entrópiának a minták együttes eloszlása szerinti várható értéke az indikátorfüggvény entrópiája vagy VC-entrópia.

$H\text{(}l\text{)}=E\left\{\text{ln }N\text{(}{Z}_l\text{)}\right\}$ . (2.21)

A VC-entrópia mind az indikátorfüggvény-halmaztól, mind a mintakészlet eloszlását jellemző együttes eloszlás- vagy sűrűségfüggvénytől függ. A VC-entrópia az ERM elv konzisztenciájában kap szerepet, ugyanis az ERM elv konzisztenciájának szükséges és elégséges feltétele, hogy teljesüljön a

$\underset{l\to \infty }{\text{lim}}\frac{H\text{(}l\text{)}}{l}=0$ (2.22)

feltétel.

Mivel ez az összefüggés a mintapontok eloszlásától függő VC-entrópiára vonatkozik, a közvetlen gyakorlati felhasználásra nem alkalmas. További „hiányossága”, hogy a feltétel csak magának a konvergenciának a tényére vonatkozik, a konvergencia-sebességről nem állít semmit. A statisztikus tanuláselmélet ugyanakkor a konvergencia eloszlásfüggetlen feltételét is megadja, amely egyben biztosítja a (2.19) összefüggés által megfogalmazott módon a gyors konvergenciát is. Ehhez a következőnek kell teljesülnie:

$\underset{l\to \infty }{\text{lim}}\frac{G\text{(}l\text{)}}{l}=0$ . (2.23)

A statisztikus tanuláselmélet a G(l) függvényt nevezi növekedésfüggvénynek (growth function), amelyet a véletlen entrópia alapján a következőképpen definiál:

$G\text{(}l\text{)}=\text{ln }\underset{z_l}{\text{max}}N\text{(}{Z}_l\text{)}$ . (2.24)

G(l) értékei eloszlásfüggetlen mennyiségek, melyek meghatározásánál az összes lehetséges l elemű mintakészletet tekintve kell a maximumot keresni. A növekedésfüggvény a mintapontok számának függvényében azon lehetséges particionálások (kétosztályos szeparálások) maximális számát (pontosabban annak logaritmusát) adja meg, melyeket az $L\left(z,w\right)$ függvényosztályba tartozó indikátorfüggvényekkel lehet megvalósítani. G(l) definíciója szerint elegendő, ha egyetlen olyan l elemű mintakészletet találunk, amely mellett a maximális számú szeparálás lehetséges. Az összes l elemű mintakészletnél nem feltétlenül kapunk azonos számban kétosztályos szeparálásokat. A növekedésfüggvény, ami az alkalmazott függvényosztálytól függ, az eloszlásfüggetlen entrópia felső korlátja. Ugyanakkor, mivel egy l elemből álló mintakészletet maximálisan 2^l-féleképpen lehet particionálni, nyilvánvaló, hogy

$G\text{(}l\text{)}\le l\text{ ln 2}$ , (2.25)

vagyis a bevezetett mennyiségek között az alábbi egyenlőtlenségek állnak fenn:

$H\text{(}l\text{)}\le G\text{(}l\text{)}\le l\text{ ln 2}$ . (2.26)

Ennek igazolásához a VC-elmélet a Jensen egyenlőtlenség alapján felhasználja, hogy

$H\text{(}l\text{)}=E\left\{\text{ln}N\text{(}{Z}_l\text{)}\right\}\le \text{ln }E\left\{N\text{(}{Z}_l\text{)}\right\}$ , (2.27)

továbbá, hogy

$\text{ln }E\left\{N\text{(}{Z}_l\text{)}\right\}\le \text{ln }\underset{z_l}{\text{max}}N\text{(}{Z}_l\text{)}=G\text{(}l\text{)}$ . (2.28)

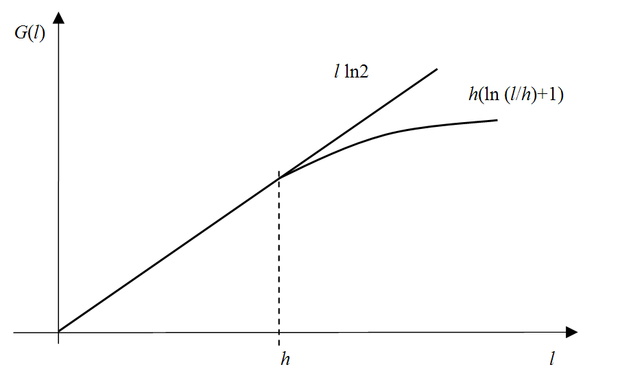
Az általánosító képességre vonatkozó eloszlásfüggetlen eredmény a növekedésfüggvény vizsgálata alapján nyerhető. Vapnik és Cservonyenkis bebizonyították, hogy a növekedésfüggvény vagy lineárisan növekszik l-lel, vagy l valamely logaritmikus függvényével felülről korlátozható, ahogy ezt a 2.6 ábra mutatja.

Az előbbi esetben

$G\text{(}l\text{)}=l\text{ ln 2}$ , (2.29)

az utóbbiban pedig

$G\text{(}l\text{)}\le h\left(1+\text{ln}\frac{l}{h}\right)$ . (2.30)

A mintapontok számának az az l értéke, ahol $G\text{(}l\text{)}$ növekedése a lineáris növekedéshez képest lelassul nevezetes érték. Ezt az értéket nevezzük VC-dimenziónak, és a továbbiakban h-val fogjuk jelölni. Ha h véges érték, akkor nagy mintaszámokra a növekedésfüggvény a lineárisnál lassabban nő.

Figyelembe véve a gyors konvergencia (2.23)-ban megfogalmazott feltételét, az ERM elv konzisztenciájának és a gyors konvergenciának eloszlásfüggetlen szükséges és elégséges feltétele, hogy a VC-dimenzió, h véges legyen. Ugyanakkor, ha a növekedésfüggvény bármekkora l mellet l-lel lineárisan nő, az adott indikátorfüggvény-készlet VC-dimenziója definíciószerűen végtelen. Ebben az esetben az adott függvényosztály elemeivel bármely l elemű mintakészletet minden lehetséges módon, tehát mind a 2^l–féleképpen lehet particionálni. Ez pedig azt jelenti, hogy az a tanuló rendszer, amelyik ilyen függvényosztályba tartozó függvények megvalósítását végzi, általánosításra nem lesz képes. Vagyis akármilyen tanítókészletünk is lesz, a tanítópontokhoz bármilyen módon is rendeljük hozzá a kívánt válaszokat − a címkéket − a tanuló rendszer a tanítópontokat mindig hibátlanul meg tudja tanulni; nem az osztályozási feladatot, hanem az adott mintapontokat tanulja meg, és így a tanítópontokra kapott válaszok alapján az általánosítóképességéről semmit sem tudunk állítani.

Fentiek alapján a VC-dimenziónak egy alternatív definíciója is megadható: egy indikátorfüggvény-készletnek h a VC-dimenziója, ha létezik h olyan mintapont, melyeket a függvénykészlet elemeivel minden lehetséges módon be tudunk sorolni két osztály valamelyikébe (a h mintapontot minden lehetséges módon két színnel ki lehet színezni), de h+1 ilyen mintapont már nem létezik. A VC-dimenzió tehát az a maximális mintaszám, amit adott függvényosztály elemeivel hibátlanul particionálhatunk minden lehetséges módon. A VC-dimenzió egy függvényosztály komplexitásának egyfajta mértékeként is tekinthető.

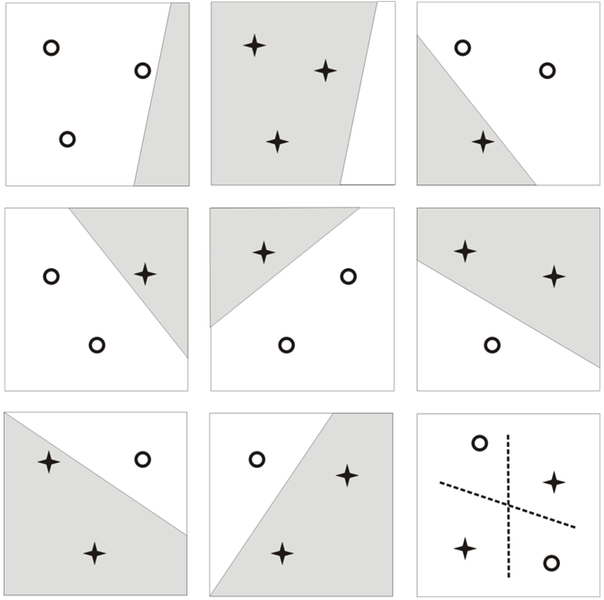
A VC-dimenzió fogalmát illusztrálja a 2.7 ábra. Tekintsük a lineáris függvények osztályát, vagyis a mintapontok particionálására a lineáris függvények osztályából válasszunk függvényeket. Ha l=3, tehát három mintapontunk van, a ponthalmaz bármely particionálása (bármilyen címkézése) lehetséges megfelelően megválasztott egyenessel. Négy pont esetén ez már nem mindig oldható meg: az összes (2⁴) lehetséges szeparálás mindegyike lineáris szeparáló függvénnyel már nem lehetséges. Az alábbi ábra a három ponthoz tartozó nyolc lehetséges kombinációt mutatja be. Jól látható, hogy a pontok bármely címkézése mellett szeparáló egyenes elhelyezhető. A négypontos esetek közül csak egy lineárisan nem megoldhatót mutatunk. Az ábra alapján meg is állapítható, hogy a lineáris szeparáló függvények osztályának VC-dimenziója kétdimenziós mintapontoknál 3.

A statisztikus tanuláselmélet fontos eredménye, hogy annak megállapításán túl, hogy véges VC-dimenzióra van szükség, felső korlátokat is meg tud fogalmazni a tanuló rendszer valódi hibájára (a valódi kockázatra). Ezek a felső korlátok összekapcsolják a tapasztalati- és a valódi kockázatot. Arra a kérdésre adnak egyfajta választ, hogy milyen közel van egymáshoz az $R\text{(}{w}^{\ast }|l\text{)}$ valódi kockázat és az $R_{\text{emp}}\text{(}{w}^{\ast }|l\text{)}$ tapasztalati kockázat. A kapcsolatban h értékének is fontos szerep jut.

Az elmélet keretében számos ilyen korlát született. Itt példaként csak két eloszlásfüggetlen korlátot említünk meg, amelyek a bináris osztályozós (kétosztályos), illetve a regressziós problémákra vonatkoznak.

Egy osztályozó valós hibájára vonatkozó következő egyenlőtlenség legalább $1-\eta$ valószínűséggel érvényes az összes $L\text{(}z,w\text{)}$ függvényre, köztük arra az $L\text{(}z,w^{\ast }|l\text{)}$ -re is, amely az l mintapont alapján számított tapasztalati kockázatot minimalizálja:

$R\text{(}w\text{)}\le R_{emp}\text{(}w\text{)}+\frac{\epsilon \text{(}h\text{)}}{2}\sqrt{1+\frac{4R_{emp}\text{(}w\text{)}}{\epsilon \text{(}h\text{)}}}$ , (2.31)

ahol

$\epsilon \text{(}h\text{)}=4\frac{h\text{(ln (}2l/h\text{)}+1\text{)}-\text{ln (}\eta /4\text{)}}{l}$ . (2.32)

Itt $h$ a modell VC-dimenziója, és l a tanítóminták száma.

A (2.31) összefüggés alapján látható, hogy a valódi kockázat felső korlátja két tagból áll: az első a mintapontok alapján számítható tapasztalati kockázat, míg a második a tanuló rendszer komplexitására jellemző VC-dimenzió értékétől (pontosabban a h/l aránytól) is függ. Jó általánosító-képesség eléréséhez ezért mind a két tag minimalizálása szükséges: önmagában a kis tapasztalati hiba nem elegendő, hiszen ez csak azt biztosítja, hogy a mintapontokat a tanuló rendszer jól megtanulta. Ha emellett a második tag értéke nagy, akkor az általánosítóképesség gyenge lesz. A már említett túlilleszkedés ilyen esetnek felel meg. A második tag, amit konfidencia tagnak is szokás nevezni, akkor vesz fel nagy értéket, ha h értéke nagy, pontosabban, ha a mintapontok számához viszonyítva nagy a VC-dimenzió értéke. Mint említettük a VC-dimenzió tekinthető úgy, mint az osztályozási feladatot megoldó rendszer által megvalósítható függvényosztály komplexitásának valamilyen mértéke. Minél nagyobb komplexitású rendszerrel valósítjuk meg a feladatot, annál nagyobb az esély, hogy a tanítópontokban a hibát tetszőlegesen kicsivé tudjuk tenni, vagyis a (2.31) összefüggésben a tapasztalati hibakomponens tetszőlegesen kicsi lehet. Ugyanakkor, ha ezzel egyidőben a második tag nő, az általánosítóképesség gyenge lesz, a valódi kockázat értéke nagy lesz.

A tanuló rendszer komplexitása függ a háló szabad paramétereinek számától. A statisztikus tanuláselmélet eredményei tehát összhangban vannak azzal a megállapítással, hogy a túl sok szabad paraméter a túlilleszkedés lehetősége miatt gyengébb általánosítóképességet eredményezhet, mint ha a szabad paraméterek számát korlátozzuk. Meg kell jegyezni azonban, hogy a statisztikus tanuláselmélet a komplexitás mérésére nem a szabad paraméterek számát, hanem a VC-dimenziót használja, ami azt sejteti, hogy a megvalósítható függvényosztály komplexitása nem csak a szabad paraméterek számával befolyásolható. Erről részletesebben a kernel gépekkel – köztük a szupport vektor gépekkel is – foglalkozó 6. fejezetben lesz szó.

A (2.31) egyenlőtlenség $1-\eta$ valószínűséggel érvényes, ahol az ( $1-\eta$ )-t konfidenciaszintnek is szokás nevezni. Minél magasabb a konfidenciaszint (minél nagyobb valószínűséggel igaz a felső korlátra vonatkozó egyenlőtlenség), annál nagyobbá válik a konfidencia tag. Kis $\eta$ mellett a felső korlát túl nagy értéket vesz fel, ami a felső korlát gyakorlati használhatóságát már megkérdőjelezi. Ez különösen kis mintapontszámnál igaz. Ha a mintapontok száma egyre nő, miközben a többi érték változatlan marad, a konfidencia tag értéke csökken, és így a tapasztalati hiba egyre jobb becslése lesz a valódi kockázatnak. Ez szintén összhangban van azzal az intuitív érzésünkkel, hogy minél nagyobb számú mintaponttal tanítunk egy hálót, annál megbízhatóbb az eredmény, és ekkor a mintapontokra vett átlagos hiba − a tapasztalati kockázat − önmagában is egyre inkább alkalmas lehet a háló minősítésére.

Az VC-dimenzióra és így az általánosító-képességre vonatkozó eredmények kiterjeszthetők regressziós feladatokra is. Regressziós esetben is megfogalmazható a valódi kockázat felső korlátja. Egy regressziós feladatnál a valódi kockázatra vonatkozó következő egyenlőtlenség legalább $1-\eta$ valószínűséggel érvényes az összes $L\text{(}z,w\text{)}$ függvényre, köztük az empirikus kockázatot minimalizáló $L\text{(}z,w^{\ast }|l\text{)}$ -re is:

$R\text{(}w\text{)}\le \frac{R_{\text{emp}}\text{(}w\text{)}}{{\left(1-c\sqrt{\epsilon \text{(}h\text{)}}\right)}_{+}}$ (2.33)

ahol $\epsilon \text{(}h\text{)}$ -t most is (2.32) adja meg és ${\text{(}a\text{)}}_{+}=\text{max(}a\mathrm{,0}\text{)}$ . A legtöbb gyakorlati problémánál az (2.33) összefüggésben a c=1 választás ajánlott.

Az előbbiek alapján nyilvánvaló, hogy a tapasztalati hiba kis értéke nem jelent egyben jó általánosítóképességet is. Az ERM elv konzisztenciájára és a gyors konvergenciára vonatkozó eredmények azt mutatták, hogy ha a mintapontszám nagy, pontosabban ha az $l/h$ arány nagy, akkor (2.31) jobb oldalának második tagja elhanyagolható: a tapasztalati kockázat közel azonos a valódi kockázat értékével. Ha azonban $l/h$ értéke kicsi, akkor nyilvánvaló, hogy a kis empirikus hibából nem következik, hogy a valódi kockázat értéke is kicsi lesz. Megfelelően kis általánosítási hibához ezért a (2.31) egyenlőtlenség jobb oldalának mindkét tagját (illetve regressziós esetben a (2.31) egyenlőtlenség jobb oldalát) minimalizálni kell. Láttuk, hogy a két hibakomponens egymás rovására csökkenthető, hiszen a komplexitás növelésével a tapasztalati hiba csökken, de a második tag nő, míg a komplexitás csökkentése ezzel épp ellentétesen hat: a második tagot tudjuk csökkenteni, de a tapasztalati hibát a kisebb komplexitású tanuló rendszer csak kevésbé tudja minimalizálni.

A komplexitás és a hiba együttes minimalizálásának formális kereteit a strukturális kockázatminimalizálás (structural risk minimization, SRM) megközelítés adja meg. Az SRM eljárás pont azt mondja ki, hogy véges (kis) mintaszámnál mindkét hibakomponenst együttesen kell minimalizálni. A módszert eredetileg Vapnik és Cservonyenkisz osztályozási feladatokra javasolták, de bármilyen tanulási feladatnál alkalmazható, amikor a kockázat értékének a minimalizálása a cél [Vap79]. Az SRM eljárás szerint a tanuló rendszer konstrukciójánál nemcsak a tapasztalati kockázatot, hanem a VC-dimenzión keresztül a modell komplexitását is kézben kell tartani.

Ennek érdekében az SRM egy egymásba ágyazottan növekvő komplexitású modellkészletet használ, azaz egyre komplexebb függvényosztályok elemeivel próbálja a feladatot megoldani. A megoldásnál használt S függvényosztály egymásba ágyazott részosztályokat

$S_1\subset S_2\subset \dots \subset S_k\subset \dots$ (2.34)

tartalmaz. Minden egyes $S_k$ részosztály véges $h_k$ VC-dimenzióval jellemezhető és az egyes részosztályok növekvő VC-dimenzió (növekvő komplexitás) szerint sorbarendezettek:

$h_1\le h_2\le \dots \le h_k\le \dots$ (2.35)

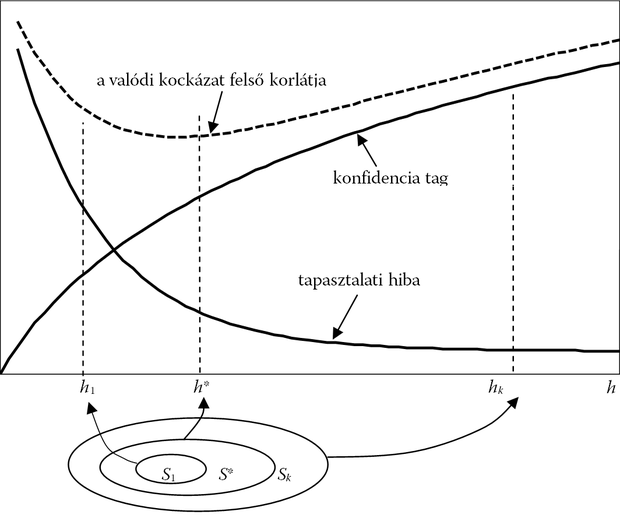
Az egyre növekvő komplexitás hatását a 2.8 ábra mutatja. Az ábrán a kockázat felső korlátja (a garantált kockázat) látható, és az, hogy ez két komponensből tevődik össze: a tapasztalati kockázatból és az ún. konfidencia-tagból. Minél komplexebb rendszert használunk, vagyis minél nagyobb a VC-dimenzió, annál kisebb lesz a tapasztalati kockázat, de ezzel együtt annál nagyobb a konfidencia-tag. Az optimumot h* mellett érjük el.

Adott mintakészlet mellett az optimális modell konstrukciója ezért az alábbi két lépésből áll: előbb a megfelelő komplexitású modellstruktúrát − a megfelelő $S_k$ részosztályt − választjuk meg, majd ezen belül végezzük el a modell konstrukciót a tanító mintapontok alapján.

A statisztikus tanuláselmélet általánosítási képességre vonatkozó eredményeinek a jelentősége az, hogy – még ha csak felső korlát formájában is, de – formális kapcsolatot teremt a tanítópontokban számított átlagos kockázat, a tapasztalati kockázat és a tényleges általánosítási hiba, a valódi kockázat között. Az elmélet gyakorlati alkalmazása azonban nehézségekbe ütközik. Egyrészt egy függvényosztály VC-dimenziójának a meghatározása általában igen nehéz. A VC-dimenzió csak néhány egyszerűbb esetben kapható meg könnyen, gyakran pedig csak meglehetősen pontatlan felső becslés adható rá. Másrészt a megfogalmazott felső korlátok általában nem éles korlátok; a gyakorlati feladatoknál az általánosítási hiba jóval kisebb, mint amit a felső korlát megad. Ezen még gyengít, ha a VC-dimenziót is csak becsüljük felülről.

A kockázatra vonatkozó felső korlátok véges VC-dimenzió mellett értékelhetők. Ebből azonban nem következik, hogy nem létezhetnek jó általánosítóképességgel rendelkező olyan tanuló rendszerek, ahol a VC-dimenzió végtelen. Egyes neuronháló típusoknál − ilyen például a leggyakrabban alkalmazott többrétegű perceptron, az MLP is − a VC-dimenzió lehet végtelen, miközben e hálótípus a gyakorlatban igen sikeresen alkalmazható. A végtelen VC-dimenzió csak azt jelenti, hogy a statisztikus tanuláselmélet alapján az általánosítóképességről itt semmit sem tudunk mondani.

Fentiek miatt a korlátokra vonatkozó eredmények neuronhálóknál általánosan nem alkalmazhatók. Hasonló mondható el az SRM megközelítésről is. Ennek ellenére az elmélet elvi jelentőségén túl fontos gyakorlati következményekkel is jár: a tanuló rendszereken belül meghatározó szerepet játszik a döntően a kilencvenes évek derekán kidolgozott szupport vektor gépek elméleti megalapozásában. A szupport vektor gépekről részletesen a 6. fejezetben szólunk.