A feladat célja érzékeltetni, hogy egy távolsági fogalom, mint irányító heurisztika, önmagában még nem biztos, hogy jó, vagy rossz. Hatékonysága egy keresés vezérléséhez azon múlik, hogy a keresés milyen keresési térben folyik, azaz, hogy a kereső ágensnek milyen lehetőségei vannak a térben mozgásra.

Egy bástya sakktáblán tetszőleges számú mezőt léphet egyenes vonalban (vízszintesen vagy függőlegesen), de más bábún át nem ugorhat. 1. Két A és B mező között bástyával minimális számú lépésben történő mozgás megtervezéséhez vajon elfogadható heurisztika-e a Manhattan-távolság? Miért igen/nem? 2. És az euklideszi távolság vajon elfogadható-e? Miért igen/nem?

A feladat megoldásához legjobban úgy jutunk el, ha egy olyan helyzetet képzelünk el, ahol a táv kisebb számú lépésben megtehető, mint a két pontra számított távolság. Ez azt fogja jelenteni, hogy a távolság, mint a keresési heurisztika nem optimista, azaz nem elfogadható.

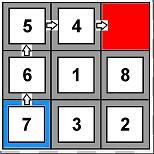
Tekintsük a bal oldali ábrát. Ha a bástya tetszőleges számú mezőt léphet egyenes vonalban, akkor az A (kék) és a B (piros) mező közötti távot két lépésben teheti meg. Az A és B pontok Manhattan-távolsága viszont 4+4=8. A keresési térben találtunk tehát egy olyan helyzetet, amikor a heurisztika nem optimista, viszont az elfogadhatósághoz heurisztikának a tér minden pontjában optimistának kell lennie, kivétel nélkül. Az 1. kérdésre a válasz tehát: nem!

Mi a helyzet az euklideszi távolsággal? A bal oldali ábrán az euklideszi távolság értéke √(4²+4²) = √(2 x 4²) = 4 x √2 > 4. Tehát ez is nagyobb, mint a tényleges távolság (2 lépés). Azaz a 2. kérdésre a válasz szintén: nem!

Buktatók: Tipikus hiba itt arra gondolni, hogy a Manhattan-távolság tili-toli játéknál, látszólag hasonló sakktábla-elrendezésű keresési térben elfogadható heurisztika. Igen, de ebben az esetben a lépések szigorúan egyetlenegy mezőnként történnek (ld. jobboldali ábra), és így a legrövidebb út sem lehet rövidebb, mint az akadálytalan elemi lépésekből számított Manhattan-távolság.

Kidolgozta: Dobrowiecki Tadeusz, BME