Gyakorlati feladatok megoldásánál a mérőeszközök, illetve a technológia hibái miatt a mért adatok hiányosak lehetnek. (Természetesen a hiánnyal azonosan kezelendő problémára vezet, ha az adat előállt ugyan a mérés során, de értéke nem hihető.) Az egyszerűbb tárgyalhatóság kedvéért tegyük fel, hogy egy folyamat P mért adatából állítjuk elő a skalár kimenet becslését neurális modellünk segítségével. Ha ellenőrzött tanítással alakítjuk ki a modellt, akkor többféle megoldandó probléma fordulhat elő (azt feltételezzük, hogy a modell több bemenettel, de egyetlen kimenettel rendelkezik):

Vizsgáljuk meg melyik hiba milyen problémát eredményez a tanítás során. (A tanított hálózat használata során a bemeneti adatok hiánya azonos jellegű problémákat vet fel, mint a tanítás során. A kimeneti adat hiányának viszont az ellenőrzött tanítás során nincs értelme, ez esetben nem tudunk tanítani ezzel a mintával. A tanított háló működtetésekor viszont természetes, hogy nincs kimeneti adat.) A feladat jellegétől függően alapvetően kétféle helyzettel kerülünk szembe. Amennyiben statikus feladattal foglalkozunk, akkor a hiányzó adatok a tanítás során csupán a modellezni kívánt mintatér lefedettségét rontják, de a többi mintára nincs hatásuk. Ha dinamikus feladattal foglalkozunk, akkor a hiányzó adatok a meglévő helyes adatok használhatóságát is zavarják. (Példa lehet a dinamikus modellezésre, ha modellünk idősorok jóslásával foglalkozik: az előző N időpontban mért értékek alapján jósolja a következő értékvektort. Egy mért érték kimaradása ilyenkor a következő N érték becslését is lehetetlenné teszi.)

Statikus eset

Statikus esetben ha a teljes bemeneti adatsor vagy a kimeneti adat hiányzik (missing data), akkor nem tehetünk mást, mint hogy töröljük a mintát a tanító (teszt) készletből. (Statikus eseten itt nem azt értjük, hogy a neurális modell statikus, hanem azt, hogy az egymás után generált adatsorok között nincs kapcsolat, az egymás után generált adatok korrelálatlanok.)

Amennyiben az N elemű bemeneti adatvektor egy vagy több eleme hiányzik, megkísérelhetjük ezek pótlását (imputation). Természetesen ez általában csak akkor kecsegtet sikerrel, ha a hiányzó elemek száma jóval kisebb N-nél. A hiányzó adat pótlására az adatsor jellegétől függően két lehetőség kínálkozik. Általában is célszerű, de ha hiányzó adatok pótlására van igény, akkor mindenképp meg kell vizsgálnunk, hogy van-e összefüggés a bemeneti adatvektor elemei között. Ezt a kovariancia mátrix vizsgálatával végezhetjük el.

A (13.7), (13.8) egyenletekkel definiált C kovariancia mátrix elemeiből képezhető a korrelációs együtthatók mátrixa, melynek elemei:

$\tilde{C}\left(i,j\right)=\frac{C\left(i,j\right)}{\sqrt{C\left(i,i\right)C\left(j,j\right)}}$ (13.31)

A $\tilde{C}\left(i,j\right)$ korrelációs együttható 1-hez közeli értéke az $x_i$ és $x_j$ komponensek közötti erős kapcsolatra utal, míg ha értéke közel 0, akkor a bemeneti vektor ezen két komponense korrelálatlannak tekinthető.

Ha egy adatkomponens egyetlen másik komponenssel sincs kapcsolatban, akkor nincs más lehetőségünk, mint hogy a hiányzó bemeneti változó értéket ugyanezen változó többi mért értéke alapján becsüljük. Tulajdonképpen a hiányzó bemeneti paraméterre konstans + zaj jelmodellt állítunk fel, és ez alapján becsüljük a hiányzó értéket. Így a hiányzó i-edik adatkomponens becslése a következő összefüggéssel történhet:

${\widehat{x}}_i={\overline{x}}_i+{\sigma }_i\xi$ (13.32)

ahol ${\overline{x}}_i$ és ${\sigma }_i$ az (13.3) és (13.4) összefüggéssel definiált, ξ pedig egy alkalmas (tipikusan 0 várható értékű, 1 szórású Gauss vagy egyenletes eloszlású) valószínűségi változó. Természetesen használhatunk ${\sigma }_i$ -nél kisebb vagy nagyobb szórást is. Gyakran egyszerűen az átlagértékkel pótoljuk a hiányzó adatokat, ekkor viszont a mintahalmaz statisztikai jellemzői megváltoznak az adatpótlás hatására.

Amennyiben a korrelációs együttható mátrix bizonyos főátlón kívüli elemei 1-hez közeli értéket vesznek fel, akkor ezen elemek közötti kapcsolat lehetőséget teremt arra, hogy az egyik elem hiánya esetén a többi komponens értékéből következtethessünk a hiányzó adat valószínű értékére. Ehhez további vizsgálatokat kell végeznünk, hiszen a korrelációs együttható csak a kapcsolat meglétét mutatja, de nem mond semmit a kapcsolat jellegére. Tulajdonképpen egy regressziós problémával állunk szemben: ha az i-edik változó hiányzik, és tudjuk, hogy az i-edik változó kapcsolatban van a j-edik változóval, akkor az $x_i^{\left(p\right)}-x_j^{\left(p\right)}p=\mathrm{1,}\mathrm{2,}\mathrm{...,}P$ ponthalmazra illeszkedő $x_i=\widehat{f}\text{(}{x}_j\text{)}$ függvényt kell megkeresnünk. Amennyiben ezt a regressziós függvényt megtaláltuk, akkor a hiányzó $x_i^{\left(h\right)}$ értéket az:

${\widehat{x}}_i^{\left(h\right)}=\widehat{f}\left(x_j^{\left(h\right)}\right)$ (13.33)

összefüggéssel becsülhetjük. Természetesen a fenti legegyszerűbb eseten kívül előfordul, hogy $x_i$ nem csupán $x_j$ -vel mutat szorosabb kapcsolatot, hanem közvetlenül vagy közvetve ( $x_i$ kapcsolatban van $x_j$ -vel, $x_j$ kapcsolatban van $x_k$ -val, stb.) más bemeneti komponensekkel is. Ezen esetekben egy többdimenziós regressziós problémával állunk szemben, és az $\widehat{f}\text{(}{x}_j,x_k,\mathrm{...}\text{)}$ regressziós függvényt kell megtalálnunk a hiányzó adat becsléséhez.

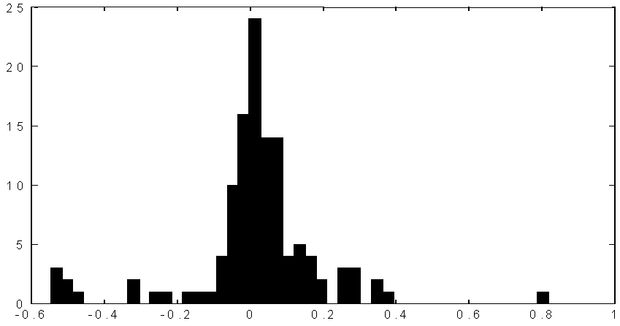
A 13.9 ábra egy konkrét ipari folyamat modellezése során végzett vizsgálat eredményét mutatja: a felhasznált 16 bemeneti paraméterből képzett korrelációs együttható mátrix elemeinek hisztogramja látható az ábrán. (A 13.31 összefüggésből látszik, hogy a mátrix főátlójában minden elem 1 és a mátrix szimmetrikus, így az ábrán csak a főátló alatti elemek hisztogramját vettük fel.

Az ábrán látható, hogy a lehetséges $\left(\begin{array}{c}16\\ 2\end{array}\right)=90$ paraméterpárból nagyságrendileg 5-10 olyan pár van, amelyek erősebb korrelációt mutatnak (jelen esetben az együttható 0,5-nél nagyobb abszolút értékét vettük szignifikánsnak).

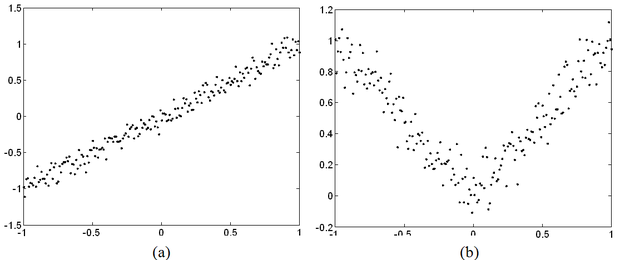
A korreláció ugyanakkor nem minden esetben mutatja meg kellő módon a komponensek közötti összefüggést. Mindkét alábbi ábrán az látható, hogy a két ábrázolt paraméter között szoros kapcsolat van, mégis a 13.10 (a) ábrán látható helyzetben a korrelációs együttható értéke nagy (0,9 feletti), míg a 13.10 (b) ábrán kicsi (0,1 alatti). A 13.3.1 pontban ismertetett EM algoritmus ugyanakkor eszközt adhat a kapcsolat felfedezésére, a pótlás segítésére.

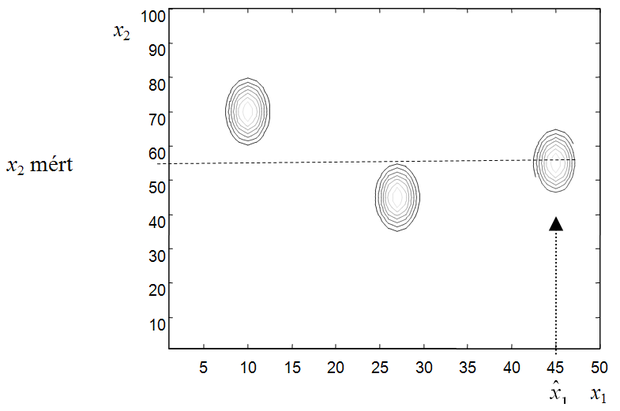
Az 13.11 ábrán demonstrációs céllal bemutatunk egy esetet, amikor a két paraméter (x₁ és x₂) között van kapcsolat, de ez egyszerű korrelációs módszerekkel nem mutatható ki jól. Ugyanakkor, ha tudunk is arról, hogy van kapcsolat a két változó között, a kapcsolat jellege más, attól függően, hogy a mintapont melyik klaszterbe tartozik. Ha ezt el tudjuk dönteni, pl. EM algoritmus segítségével, akkor az ismert x₂ alapján (x₂ mért, szagattot vonal) jó becslést tudunk adni hiányzó x₁-re. Ha a mintapontok eloszlásáról van ismeretünk (pl. az ábrán látható módon azok 3 klaszterben helyezkednek el) és az egyes klaszterek a priori előfordulásai azonosak, akkor a feltételes valószínűségek alapján az ismert x₂-höz a hiányzó x₁ pótlására a legnagyobb valószínűséggel ${\widehat{x}}_1$ felel meg.

Dinamikus eset

Amennyiben dinamikával rendelkező folyamat modellezésénél találkozunk hiányzó adatokkal, akkor a statikus esetben használtakon túlmenően új lehetőségeink nyílnak az adatok pótlására.

Alapvetően azon változók, változócsoportok hiányzó értékeit tudjuk a statikus esethez képest jobban pótolni, amelyeknél legalább rövidtávú trendeket fedezhetünk fel a változó időbeli alakulásában. Az időbeli összefüggések felderítésére egyszerű esetekben az időfüggvény tanulmányozása is elegendő, de általában az autokorrelációs függvény vizsgálata szolgálja ezt a célt.

$R_i\left(t,\tau \right)=E\left\{x_i\left(t\right)x_i\left(t+\tau \right)\right\}$ (13.34)

Ha az autokorrelációs függvény a $\tau$ valamilyen tartományában nagy értékeket vesz fel, akkor a hiányzó $x_i\text{(}t\text{)}$ az $x_i\text{(}t+\tau \text{)}$ segítségével pótolható.

Gyakran találkozunk olyan helyzettel, mikor az autokorrelációs függvény τ valamilyen tartományában − például 0-hoz közeli τ-k esetén − t-től függetlenül nagy érték. Ez arra utal, hogy rövid távon a változó erős trendet mutat: ilyenkor a tanító mintakészletnél lehetőségünk van a hiányzó értéket az időben megelőző és követő értékek alapján interpolálni, illetve a tanított hálózat működése során az időben megelőző minták alapján extrapolálhatunk a hiányzó aktuális értékre.

Tehát ha az adatokat valamilyen − legalább rövidtávú trendeket generáló – folyamat hozza létre, akkor a teljes N elemű bemeneti vektor, vagy a kimeneti érték hiánya is pótolhatóvá válik. Természetesen a statikus esetre ismertetett módszerek a paraméter időbeli alakulását figyelembe vevő módszerekkel kombinálhatók.