Az előző fejezetben bemutattuk, hogy akár a Hebb-szabály alkalmazásával, akár egy alkalmas energiafüggvény megválasztásával a súlyok általában meghatározhatók úgy, hogy a tárolandó minták vonzási pontok legyenek a konfigurációs térben, azaz lokális minimumai legyenek a rendszerhez tartozó energiafüggvénynek. A hálózat egy (Hamming távolság értelemben) megfelelően közeli konfigurációból, a vonzási körzet valamely pontjából indítva, a dinamikus működés során a kívánt állapotban fog stabilizálódni.

Az ideális az volna, ha a teljes konfigurációs teret kitöltenék a tárolt minták és ezek vonzási körzetei, mivel így tetszőleges állapotból indítva a hálózatot, az a legjobban "hasonlító" tárolt mintára asszociálna. A helyzet természetesen nem ilyen szép. A tanított konfigurációkon kívül számos más vonzási pont is létezik. Ezek típusait igazolás nélkül ismertetjük:

• az összes tárolt minta inverzéhez (-x_i^(α)) is lokális minimum tartozik,

• olyan ún. kevert állapotok is vonzási pontok, amelyek páratlan számú tárolt minta lineáris kombinációiból állíthatók elő. Például ilyenek az alábbi állapotok: $a_i^{\text{kevert}}=\text{sgn(}\pm a_i^{\left({\alpha }_1\right)}\pm a_i^{\left({\alpha }_2\right)}\pm a_i^{\left({\alpha }_3\right)}\text{)}$ ,

• nagyméretű hálózatokban viszonylagosan nagyszámú tanított minta esetén bizonyítható, hogy kialakulnak olyan lokális minimumok, amelyek nem korreláltak a minták semmilyen részhalmazával sem.

Bár az utóbbi két osztályba sorolt vonzási pontokhoz magasabb energiaértékek tartoznak és általában kisebb a vonzási körzetük is, a rendszer ezekben a hamis lokális minimumokban is stabilizálódhat. Célunk mindenképpen az, hogy elkerüljük a "nem kívánt" lokális minimumokba történő beragadást. A helyes, optimális megoldáshoz tartozó állapot megtalálása egy adott hálózat esetén a kiindulási konfigurációtól függ. A kezdeti állapot az alkalmazások többségében vagy adott, vagy nincs is információnk ennek megfelelő megválasztásáról, így a legtöbb alkalmazás esetében célszerű a Hopfield hálózat működési algoritmusának módosítása.

Az említett hátrányos tulajdonságok kiküszöbölésére többféle ötlet is adódik:

A következő fejezetben olyan módszert mutatunk be, amely ez utóbbi lehetőséget használja a globális minimum, de legalábbis egy kis energiájú lokális minimum megtalálására.

A lokális minimumok elkerülésére leggyakrabban az ún. szimulált lehűtés módszert alkalmazzák a Hopfield hálóknál. A hálózat ilyen kiterjesztését Boltzmann gépnek vagy szimulált lehűtés hálózatnak hívjuk [Aar89].

A módosítás alapgondolata, hogy változtassuk sztochasztikussá a minimum-keresési eljárást úgy, hogy az lehetőséget adjon a lokális minimumokból történő kikerülésre. Ezzel tulajdonképpen bizonytalanságot, azaz zajt viszünk be a folyamatba, ami "kiütheti" a kevésbé mély lokális minimumokból a rendszert, és így az nagyobb eséllyel stabilizálódhat a legmélyebb, globális minimumban [Pav05].

A módszer nevét a szilárd anyagok hőkezelésekor használt hasonló elvű módszerről kapta. Az anyagot először felhevítik, majd lassan lehűtik, és így nem a magasabb energiájú metastabil állapotokban, hanem a szabályos rácsszerkezethez tartozó alacsony energiájú állapotban szilárdul meg.

A szimulált lehűtés tehát a determinisztikus minimumkeresési eljárás helyett sztochasztikus keresést eredményez. A módszer alkalmazása a Hopfield hálózatok esetében a determinisztikus működésű neuronok sztochasztikus egységekkel való felváltását jelenti.

A modell neuronjainak működése egy sztochasztikus szabállyal írható le, amely meghatározza az értékváltások utáni lehetséges állapotok kialakulásának valószínűségét:

$P\left(x_i=\pm 1\right)=f_T\left(s_i\right)=\frac{1}{1+\text{exp}\left(\frac{\mp s_i}{T}\right)}\text{}\text{}\text{, ahol }{s}_i={\displaystyle \sum _j{w}_{ij}{x}_j+{\Theta }_i}$ (11.21)

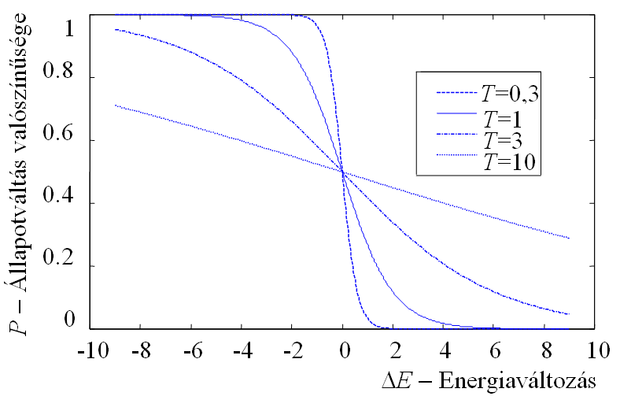
A neuronok véletlenszerű viselkedését szabályozó T paramétert az analógia alapján pszeudo-hőmérsékletnek, vagy csak egyszerűen hőmérsékletnek nevezik. A (11.21) szerinti szigmoid karakterisztika meredekségét a T paraméter határozza meg, magas T értéknél a karakterisztika lapos, míg ha a paraméter 0-hoz tart, akkor a görbe konvergál a determinisztikus hálózat transzfer függvényéhez, a (11.2) szerinti lépcsőfüggvényhez. Ez azt jelenti, hogy magas hőmérsékleten a neuronok a bemeneti gerjesztésüktől függetlenül véletlenszerűen váltanak értéket, míg a hőmérséklet paramétert csökkentve a rendszer egyre inkább a determinisztikus modellhez közelít. A hálózat működését most is tudjuk jellemezni az energiafüggvény felhasználásával. A Boltzmann gépnek a (11.21) definícióval ekvivalens leírása a következő:

$P\left(x_i\to -x_i\right)=\frac{1}{1+e_{}^{\frac{\Delta E}{T}}}\text{, ahol }\Delta E=E\left(-x_i\right)-E\left(x_i\right)$ (11.22)

Az energiaminimum elérését vagy megközelítését a fizikai analógia alapján a szimulált lehűtés módszerével végezzük. A rendszert egy magas kezdeti hőmérsékletről indítva, a hőmérséklet paraméter lassú csökkentése mellett működtetjük, míg a hálózat stabil állapotba nem kerül. Ha a rendszert megfelelően lassan hűtjük, akkor egy adott hőmérsékleten egyensúlyi állapotba kerül.

A kialakuló egyensúlyban a hálózat egy $E_k$ energiájú $x_k$ állapotba való kerülésének valószínűségét a Boltzmann eloszlás írja le:

$P\left(x=x_k\right)=q_k\left(T\right)=\frac{1}{Z\left(T\right)}{e}^{\frac{-E_k}{T}}$ , (11.23)

ahol $q_k\left(T\right)$ stacionárius eloszlásban a Z(T) partíciós függvény definíciója egy az összes lehetséges állapoton elvégzett összegzés:

$Z\left(T\right)={\displaystyle \sum _j{e}^{\frac{-E_j}{T}}}$ (11.24)

Amennyiben a rendszer lehűtése során biztosítjuk az aktuális hőmérsékleten az egyensúlyi állapot kialakulását, akkor a hálózat konvergenciáját a következőképpen vizsgálhatjuk:

$\underset{T\to 0}{\text{lim}}{q}_k\left(T\right)=\underset{T\to 0}{\text{lim}}\frac{e^{\frac{-E_k}{T}}}{{\displaystyle \sum _j{e}^{\frac{-E_j}{T}}}}=\underset{T\to 0}{\text{lim}}\frac{e^{\frac{E_{\text{min}}-E_k}{T}}}{{\displaystyle \sum _j{e}^{\frac{E_{\text{min}}-E_j}{T}}}}$ (11.25)

A zérus hőmérséklethez tartozó határértéket külön felírva az $E_{\text{min}}$ energiaminimummal rendelkező $x_k\in X_{\text{min}}$ globális minimumhelyekhez tartozó állapotokra és az $E_k>E_{\text{min}}$ energiájú $x_k\notin X_{\text{min}}$ állapotokra a következőket kapjuk:

$\begin{array}{l}\forall x_k\in X_{\text{min}}:\underset{T\to 0}{\text{lim}}{q}_k\left(T\right)=\underset{T\to 0}{\text{lim}}\frac{1}{{\displaystyle \sum _j{e}^{\frac{E_{\text{min}}-E_j}{T}}}}=\frac{1}{\left|X_{\text{min}}\right|}\\ \forall x_k\notin X_{\text{min}}:\underset{T\to 0}{\text{lim}}{q}_k\left(T\right)=\underset{T\to 0}{\text{lim}}\frac{e^{\frac{E_{\text{min}}-E_k}{T}}}{{\displaystyle \sum _j{e}^{\frac{E_{\text{min}}-E_j}{T}}}}=0\end{array}$ (11.26)

Tehát a hálózat a szimulált lehűtés ideális alkalmazásával aszimptotikusan konvergál az optimális megoldásokhoz tartozó állapotok halmazába, azaz az eljárás mentes a lokális minimumba való beragadás problémájától. Az alkalmazások szempontjából azonban fontos, hogy véges idejű lehűtést alkalmazhassunk. A szimulált lehűtés algoritmus tulajdonságai ilyen szempontból is kedvezőek. A lehűtés során az optimális megoldáshoz tartozó állapotba kerülés valószínűsége folyamatosan nő a hőmérséklet csökkentésével, ugyanakkor minden más állapothoz található egy olyan hőmérséklet küszöb érték, ami alatt az adott állapot előfordulási gyakorisága monoton csökken. Ez az eredmény az aktuális hőmérsékletekhez tartozó egyensúlyi állapotokra vonatkozik. Azonban általánosan is igaz, véges idejű lehűtés esetére is, hogy minél lassabb lehűtést alkalmazunk, annál nagyobb a valószínűsége annak, hogy a hálózat alacsony energiájú állapotba kerül.

A Boltzmann hálózat gyakorlati alkalmazásához meg kell határozni a hőmérséklet paraméter változatásának algoritmusát, az ún. lehűtési stratégiát. A lehűtési stratégia a következő elemeket tartalmazza:

• kezdeti hőmérséklet $\left(T_0\right)$

-A rendszert olyan magas hőmérsékletről indítjuk, amelyen a neuronok véletlenszerűen változtatják állapotukat. A hőmérséklet csökkentését azonnal meg lehet kezdeni, mivel ezen a hőmérsékleten a rendszer kezdettől fogva egyensúlyi állapotban van.

• lehűtés szabályozó függvény, amelynek 2 komponense a következő:

-Az adott hőmérsékleten elvégzendő állapotváltozások száma,

-A hőmérséklet csökkentésének mértéke.

-A lehűtés sebességét meghatározó függvény paramétereit a feladat megoldására rendelkezésre álló idő és az adott számítási környezet által meghatározott állapotváltozási sebesség korlátozza a gyakorlatban. Egy elterjedt heurisztikus módszer, hogy a hálózat méretének kisszámú többszöröse számú (tipikusan 3N-15N) neuron frissítése történjen meg egy adott hőmérsékleten, majd a hőmérsékletet egy 1-hez közeli faktorral szorozva csökkentjük ( $T_{k+1}=c{T}_k$ ), ahol c értéke általában 0.8 és 0.99 közötti).

• megállási feltétel

-A szimulációt akkor lehet befejezni, ha a rendszer energiája nem változik egy megfelelően hosszú iteráció során. Mivel a hőmérséklet csökkentésének módszere általában olyan, hogy ez az érték aszimptotikusan konvergál a 0-hoz, ezért a minimumhelyekből való kijutás mindvégig lehetséges. Alacsony hőmérsékletnél azonban ez a valószínűség már olyan kicsi, hogy feltételezhető, hogy a rendszer egy stabil állapotot talált meg. Ezt ellenőrizhetjük a leállás után a hőmérséklet paraméter 0-ra állításával, azaz a determinisztikus hálózattal.

Számos más lehűtési stratégia is ismert a szimulált lehűtés módszerhez, amelyek közül bármelyik felhasználható a Boltzmann hálózat működtetéséhez. A hőmérséklet csökkentésének mértékét szokásos még logaritmikus vagy polinom függvény formájában is definiálni.