A Hopfield hálózat a legegyszerűbb neurális hálózat, amely asszociatív memóriát valósít meg. Az egyrétegű visszacsatolt struktúrát John Hopfield amerikai biológus publikálta először [Hop82]. A hálózatot leggyakrabban autoasszociatív feladatok megoldására használjuk. Ilyenkor a memóriában mintákat, gyakran digitalizált képeket tárolunk [Egm02]. A neurális hálózattól azt várjuk, hogy a tárolt információ zajos, torzított, esetleg hiányos változatának megmutatásakor az eredeti mintára asszociáljon.
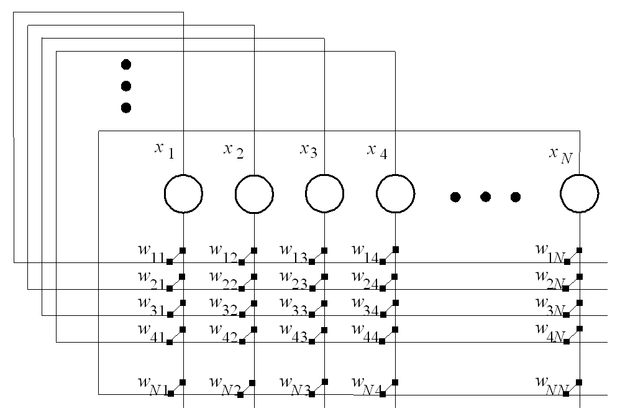
A Hopfield hálózat legegyszerűbb megvalósítását mutatja a 11.1 ábra. Az egyrétegű modellben a neuronok kimenetei minden neuron bemenetére súlyozott összeköttetéseken keresztül vannak visszacsatolva. A hálózat bemenetének a neuronok kezdeti állapotai tekinthetők, míg a kimenetet ugyanezen neuronok állapotai jelentik a működés során.
Az alapmodell esetében a Hopfield hálózat neuronjai kétértékűek. Az egyszerűbb matematikai leírás kedvéért a továbbiakban az aktív egységek értéke xi=+1, míg az inaktívaké xi=−1 legyen. (A bemutatásra kerülő igazolásokban az xi=2ui−1 konverziót használva vissza lehet kapni a jobban megszokott, az itt használttal teljesen egyenértékű 0−1 bináris kódolást.) Ezek alapján a hálózat dinamikáját a következőképpen írhatjuk fel:
, (11.1)
ahol
(11.2)
(A következőkben bemutatásra kerülő, véletlen mintákat feltételező vizsgálatoknál a Θ küszöbérték használata nem szükséges, így Θ=0-t feltételezve elhagyjuk.)
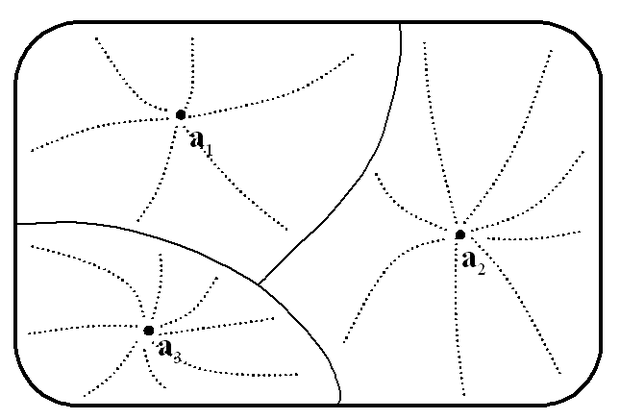
A hálózat neuronjainak egy adott állapotát egy konfigurációnak nevezzük, az összes lehetséges állapotot, pedig konfigurációs térnek. Ebben a térben a stabil állapotokhoz tartozó pontokat vonzási pontoknak nevezzük. A megfelelően beállított súlyokkal rendelkező hálózattól azt várjuk, hogy az adott kezdeti konfigurációból kiindulva az ehhez legközelebbi vonzási pontba stabilizálódik. Az egy-egy vonzási ponthoz tartozó vonzási körzet sematikus rajzát mutatja a 11.2 ábra.
A hálózat működtetésének (akár hardver megvalósításról, akár szoftver szimulációról van szó) alapvetően kétféle módja van: szinkronvagy aszinkronütemezés.
Szinkron rendszer esetén az összes neuront minden időlépésnél egyszerre módosítjuk. Aszinkron működésnél viszont egy pillanatban csak egy egység válthat értéket. Ide szokták sorolni azt az esetet is, amikor az egységek egymástól függetlenül, véletlenszerűen választják meg állapotuk módosításának időpontját, mivel ilyenkor elhanyagolhatóan kicsi annak a valószínűsége, hogy egyszerre több neuron is értéket váltson. Mind a biológiai, mind a mesterséges neurális hálózatok esetében természetesebb az aszinkron működés feltételezése, így a továbbiakban mi is ezt vizsgáljuk. (Meg kell jegyezni, hogy az aszinkron és szinkron rendszerek dinamikus tulajdonságai különböznek. Az első esetben a hálózat szomszédos konfigurációkon keresztül jut el a vonzási pontba, míg az utóbbi módszert használva a rendszer bármely állapotváltozás során a konfigurációs tér bármely pontjába kerülhet.)
A hálózatot egy adott kiindulási konfigurációból addig működtetjük, amíg stabil állapotba nem kerül. A rendszer válaszának a stabil állapothoz tartozó konfigurációt tekintjük.
A hálózat tanítása, a megjegyzendő minták tárolása, itt is a súlyok megfelelő beállításával történik. Az elsőként bemutatásra kerülő módszernél, a tanítás a módosított Hebb szabállyal történik, amit itt felügyelt tanítási eljárásként alkalmazunk, mivel a bemeneti minták egyben a kívánt kimenetek is. A tanítás során minden egyes tárolandó mintát egyszer adunk a hálózat bemenetére és ennek alapján határozzuk meg a súlyokat. Az eljárás során, az eddig bemutatott iteratív módszerektől eltérően, minden mintát csak egyszer használunk fel a súlyok meghatározásakor. A Hebb-szabály alapgondolatát a 11. fejezet már ismertette. Itt most azt fogjuk bemutatni, hogy hogyan valósítható meg a tanulás a Hopfield hálózatokon ezzel az algoritmussal.
Az egyszerűség kedvéért nézzük meg először, hogy hogyan képes a hálózat egyetlen mintát megjegyezni. A tanulás eredményeképpen a megtanulandó mintákhoz tartozó konfigurációnak stabilnak kell lennie és minél nagyobb vonzási körzetnek kell hozzá tartoznia. Egy minta stabil, ha
-re (legyen a vektor a tanítandó minta):
, (11.3)
mivel ekkor a dinamikus szabály nem okozza a neuron értékének váltását. Válasszuk a súlyokat a következőképpen:
(11.4)
Könnyen belátható, hogy a tanított minta így stabil, hiszen aj2=1. Később bemutatásra kerülő szempontok miatt az arányossági tényezőt válasszuk 1/N-re, ahol N a neuronok száma:
(11.5)
Az így meghatározott súlyokkal a hálózatban a minta nemcsak stabil, de jelentős vonzási körzete van, pontosan a konfigurációs tér fele. Egy neuron akkor vált a kívánt értékre, ha a bemenetén keletkező összeg si előjele megegyezik a minta megfelelő bitjének előjelével:
(11.6)
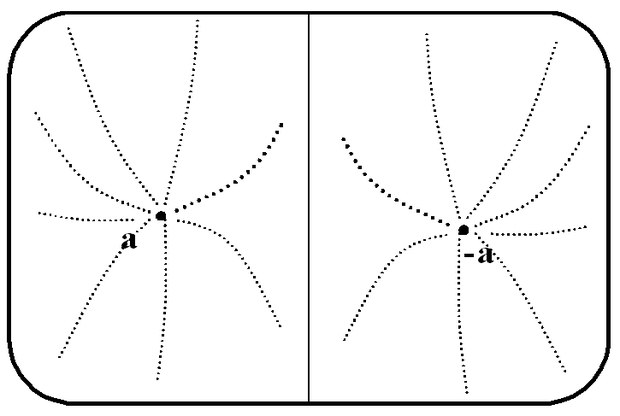
Tehát az előbb említett feltétel akkor teljesül, ha a felismerendő minta bitjeinek több mint a fele helyes, azaz a tanítottéval megegyező. Az is látható, hogy ennek a hálózatnak két stabil állapota van: a tárolt minta és annak inverze (11.3 ábra ).
Természetesen a hálózat gyakorlati alkalmazás szempontjából csak akkor lehet érdekes, ha számos minta "megjegyzésére" képes. Az előző szakaszban használt ötletet próbáljuk meg itt is alkalmazni, és a súlyok kiszámításakor vegyük az egy minta tárolására használt tagok szuperpozícióját:
, (11.7)
ahol l a tanítandó minták száma (az eddig használt nagy P betűt a valószínűség jelölésére alkalmazzuk ebben a fejezetben), és α ezek indexe.
Vizsgáljuk meg, hogy az a(α) minták stabil állapotai lesznek-e a rendszernek. A stabilitási feltétel most a β indexű mintára:
, (11.8)
ahol az si(β) összeg:
(11.9)
Az összegből az α=β -hoz tartozó tagokat:
(11.10)
Látható, hogyha a második, keresztkapcsolat tag ai(β) -vel megegyező előjelű, vagy ellentétes előjelű és 1-nél kisebb abszolút értékű, akkor a tárolt mintának ez a bitje stabil. Mint majd látni fogjuk ez a feltétel megfelelően kis számú minta tanításakor nagy valószínűséggel igaz. Ilyenkor a tárolt mintákhoz stabil állapotok tartoznak. A tárolt mintáktól valamilyen kis távolságban lévő konfigurációkból indítva a hálózatot a tárolt mintához tartozó állapotban stabilizálódik a rendszer, azaz képes hibás, zajos, hiányos minták helyreállítására, felismerésére. A vonzási körzet mérete természetesen függ a tanított minták számától, egymáshoz viszonyított elhelyezkedésüktől.
Most nézzük meg hány minta tárolható egy adott méretű hálózatban. Mivel ez függ a konkrét tanítandó példáktól, így azért, hogy legalább becslést tudjunk tenni, véletlenszerűen választott mintákat feltételezünk. Először vizsgáljuk meg a stabilitást egy véletlenszerű minta egy bitjére. A keresztkapcsolat tag hatásának egyszerűbb elemezhetősége céljából képezzük a tagot -ai(β) -vel szorozva a következő kifejezést:
(11.11)
A fent elmondottak szerint, ha Ci(β) kisebb, mint +1, akkor a β-adik minta i-edik bitje stabil. Látható, hogy Ci(β) kizárólag a tárolt mintáktól függ. Ezek alapján az instabilitás valószínűségét becsüljük: Perror = P( Ci(β) >1 ).
A Ci(β) összeg N(l-1) véletlenszerű előjelű, 1/N abszolút értékű tagból áll, és nagy l és N értékeket feltételezve, Ci(β) közelíthető egy 0 várható értékű és
szórású Gauss eloszlással:
(11.12)
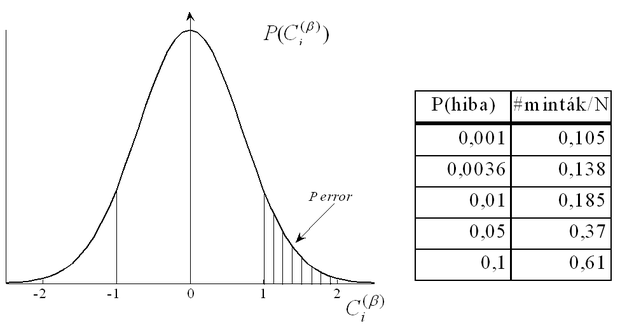
Az eloszlást és néhány hibaértékhez tartozó lmax/N arányt mutat be a 11.4 ábra. Ez például azt mutatja, hogyha azt kívánjuk, hogy egy minta egy bitje 0.999 valószínűséggel legyen stabil, akkor egy 1000 neuront tartalmazó hálózatban 105 mintát tárolhatunk. Hasonló módon lehet az összes minta összes bitjére valószínűségi állítást megfogalmazni. Szintén véletlenszerű példákat tekintve erre az esetre jó közelítésnek vehető a lmax=N/logN arány. Mivel ez az eredmény a leírt feltételek esetén igaz, így célszerű az alkalmazásoknál ennél kisebb lmax /N arányt választani.
A Hopfield hálózatok az eddig bemutatott autoasszociatív jellegű problémákon kívül használhatók heteroasszociatív feladatok megoldásra is, ahol a tanítás során a bemenetekhez önmaguktól eltérő kimeneteket rendelünk (pl. osztályozási feladatok). Ilyenkor a neuronok egy része a minták bemeneti elemeinek felelnek meg, míg a másik, kisebb részét (tipikusan 10-20%-át) kimenetnek tekintjük. Így a tanítás során a tárolandó minták a bemeneti vektorokból és a hozzájuk tartozó kívánt kimenetekből állnak.
Teszteléskor és a már betanított hálózat alkalmazásakor a bemenetekhez tartozó neuronok kezdeti állapotát a bemeneti minta szerint állítjuk, míg a kimenetet reprezentáló neuronokat tetszőleges értékűekre inicializálhatjuk. Ha a hálózat súlyait korábban sikerült megfelelően beállítani, akkor az autonóm működés során a hálózat egy olyan állapotban stabilizálódik, amelyben a bemeneti neuronok kezdeti értéküket veszik fel, míg a kimeneti neuronok arra az értékre állnak be, amelyet a tanítás során az adott bemenethez kívánt kimenetként megadtunk.
11.1.2. Az energiafüggvény
A Hopfield modell egyik előnyös tulajdonsága, amit később majd alkalmazásoknál ki is használunk, hogy egyszerűen rendelhető hozzá energiafüggvény. A rendszer minden konfigurációjához egy "energia" értéket lehet meghatározni, és ezzel meghatározunk egy a konfigurációs tér fölött értelmezett energia felületet.
Az energiafüggvény (amely Ljapunov függvényként használható) alapvető tulajdonsága, hogy az autonóm rendszer működése során értéke mindig csökken vagy változatlan marad. Tehát egy tetszőleges konfigurációból elindított hálózat az energiafüggvény valamely lokális minimumpontjában fog stabilizálódni, azaz a vonzási pontok az energiafelület lokális minimumai [Bru90]. Ha a súlyokat sikerül úgy megválasztani, hogy a tárolandó minták a minimumpontokba essenek, akkor a rendszer vizsgálható az energiafüggvény alapján.
A hálózatra felírható energiafüggvény a következő:
(11.13)
Ha a felírt képlet energiafüggvénye a hálózatnak, akkor ennek definíciójából következő tulajdonsága, hogy autonóm működés során értéke csökken vagy nem változik. Az energiafüggvény megfelelősségét igazolandó vizsgáljuk meg a rendszer energiaváltozását egy állapotváltozás során:
(11.14)
ahol
(11.15)
Aszinkronműködésű hálózat minden állapotváltozásakor pontosan egy neuron vált értéket. Ha a súlyok mátrixa szimmetrikus (
), akkor a r-edik (
, ahol N a neuronok száma) neuron értékváltását vizsgálva a következőt kapjuk:
(11.16)
Mivel a (11.1) képlet szerint
határozza meg a neuron értékváltását, így
és
előjele megegyezik, azaz az első tag értéke nem lehet pozitív. Így, ha a
visszacsatoló súlyok nem negatívak, akkor az energia változás értéke nem lehet pozitív, azaz a (11.13) összefüggéssel definiált függvény valóban Ljapunov függvénye a rendszernek.
Néhány megjegyzést érdemes tenni a fenti eredménnyel kapcsolatban. Bár a súlymátrix szimmetrikusságának megkötése erős feltétel, az alkalmazások jelentős részénél ez nem okoz problémát. Ilyen súlymátrixot eredményez az említett Hebb szabály alkalmazása és a gráfelméleti alapokra visszavezethető optimalizációs problémák jelentős részénél is természetesen adódik a szimmetrikus mátrix megválasztása. Az önvisszacsatoló kapcsolatok súlyára az energiafüggvény hozzárendelés szempontjából csak a nem negatív érték a feltétel, de megmutatható, hogy a hálózat dinamikáját előnytelenül befolyásolja, ha értékeit 0-nál nagyobbra választjuk. A pozitív önvisszacsatoló súlyok hatásának lényege, hogy nem kívánt stabil állapotokat hozhatnak létre a rendszerben, sőt egy a többi paramétertől függő érték felett akár egy neuronnak mindkét állapota is stabil lehet a többi neuron értékétől függetlenül.
Az önvisszacsatoló súlyok 0-ra választásának van egy további előnye is. Ilyenkor a (11.16) egyenlet értelmében nemcsak az igaz, hogy az autonóm hálózat állapotváltása egyértelműen meghatározza az energiafüggvény értékváltozásának előjelét, de a kapcsolat fordított irányban is közvetlen. Tehát ebben az esetben az aszinkron hálózat akkor és csakis akkor vált értéket, ha az energiafüggvény értéke csökken. Ez a gyakorlat számára azt jelenti, hogy a neurális hálózat szimulációja és az energiafüggvény szomszédos állapotokon keresztül történő minimalizálása ekvivalens eljárások, így választhatjuk közvetlenül ez utóbbit is egy probléma szimulációval történő megoldására.
A párhuzamos, szinkron ütemezésű Hopfield modell dinamikus tulajdonságai lényegesen eltérnek az aszinkron modellétől. A stabilitás vizsgálatát itt is a (11.13) szerint definiált energiafüggvény változásával végezhetjük el:
(11.17)
Az első tag értéke az aszinkron modellnél leírt indoklás miatt itt sem pozitív. A második tagra ugyanez a feltétel − a benne szereplő szorzat miatt − akkor igaz, ha a W súlymátrix pozitív szemidefinit. A szinkron modell esetében tehát elégséges feltételként a súlymátrix pozitív szemidefinit tulajdonsága szerepel, ami azt jelenti, hogy a főátlóban lévő értékeket általában nem választhatjuk 0-ra, és az sem igaz, hogy a rendszer mindig állapotot vált, ha ezzel az energiafüggvény csökkenne. Ha a súlymátrixot az aszinkron modellnél alkalmazotthoz hasonlóan, itt is szimmetrikusra választjuk 0 értékű főátlóbeli elemekkel, akkor a szinkron modell vagy egy stabil állapotba vagy egy 2 hosszúságú határciklusba konvergál. Energiafüggvény létezésére a fentieknél általánosabb feltételek is ismertek, amely szerint ún. kvázi szimmetrikus súlymátrix is stabil rendszert eredményez, de ezek az eredmények közvetlenül nem használhatóak fel a hálózatok alkalmazásakor.
11.1.3. Az energiafüggvény felhasználása
Először azt mutatjuk be, hogy az előző fejezetben bevezetett energiafüggvény és a korábban ismertetett Hebb-szabály alkalmazása azonos súlyok meghatározásához vezet. Induljunk ki most az energiafüggvényből. Próbáljuk ezt úgy megválasztani, hogy minimumpontjai a tárolandó minták legyenek. Egyetlen tanítandó minta esetében ez egyszerűen biztosítható. Az energiafüggvény minimuma legyen ott, ahol a minta és a konfiguráció átfedése (megegyező értékű bitek száma) maximális:
, (11.18)
ahol az 1/N-es szorzó csak a korábbi képletekkel való hasonlóság kedvéért szerepel. Több minta esetében is a tárolt minták az energiafüggvény minimumai kell, hogy legyenek. Az itt alkalmazott módszer szerint határozzuk meg az energiafüggvényt úgy, hogy az egyes mintákhoz választható optimális függvények szuperpozícióját vesszük:
(11.19)
A tagokat kibontva és átrendezve a következőket kapjuk:
(11.20)
Látható, hogy a Hopfield hálózathoz definiált eredeti energiafüggvényt kaptuk vissza, feltételezve, hogy a súlyokat a Hebb-szabály szerint választjuk. Ez az eredmény a gyakorlatban is jól alkalmazható. Keressünk egy olyan függvényt, amely energiafüggvénye a rendszernek és minimumpontjai az adott feladat megoldásaihoz, a tanított mintákhoz tartozó konfigurációknak felelnek meg. Ha sikerül ilyet találni, akkor a tagok szétválasztásával a hálózat súlyai meghatározhatók, azaz létre tudunk hozni egy, a problémát megoldani képes hálózatot.
Tisztázni kell még, hogy milyen alakú tagokat tartalmazhat a választandó energia-függvény. Bebizonyítottuk, hogy a
alakú tagok alkalmazhatók. Nyilván nem jelent gondot, ha a függvény konstanst is tartalmaz. Ezenkívül megfelelnek a feltételeknek a
alakú tagok is, mivel ezek felfoghatók egy konstans 1 értékű x0 neuron és az xi közötti kapcsolathoz tartozó tagnak. Azonban a
alakú, illetve magasabb-rendű kifejezések már nem értelmezhetőek a bemutatott struktúrájú Hopfield hálózat energiafüggvényében.
Meg kell még jegyezni, hogy szoftver megvalósítás esetében nem feltétlenül kell a hálózat működését szimulálni. Ha a neuronok önvisszacsatoló súlyait 0-ra választjuk (wii=0), akkor (11.16) szerint nem csak az lesz igaz, hogy a hálózat autonóm működése során az energiafüggvény csökken, de az is, hogyha az energiafüggvény csökkenne egy neuron értékváltásakor, akkor a neuron értéket is vált. Ilyenkor a hálózat szimulációja és az energiafüggvény minimalizálása ekvivalens eljárások, így választhatjuk közvetlenül ez utóbbit a probléma megoldására. Ezt a módszert néhány alkalmazási példával illusztráljuk a 11.2. fejezetben.
Szinkron működésű hálózat esetén is igaz, hogy (11.13) energiafüggvénye a rendszernek, ha a súlyokat a Hebb-szabály (11.7) alapján határozzuk meg. Ennél általánosabb elégséges feltétel a hálózat stabilitására a súlymátrix pozitív szemidefinitre választása. Hangsúlyozni kell, hogy ilyenkor általában az önvisszacsatoló súlyok nem választhatók önkényesen 0-ra (nem feltétlenül maradna a súlymátrix pozitív szemidefinit), és így az sem igaz, hogy a rendszer mindig állapotot vált, ha ezzel az energiafüggvény csökkenne ismétlés. Bár az energiafüggvény lokális/globális minimumai itt is stabil állapotai a rendszernek, a szinkron Hopfield hálózatnak (ellentétben az aszinkronnal) nem minden stabil állapota lokális/globális minimum. Ez azt jelenti, hogy a rendszerben "nemkívánatos" stabil állapotok jelennek meg. Előnye viszont az aszinkron hálózathoz képest, hogy könnyebben kerül ki a rendszer a lokális minimumokból, mivel nemcsak szomszédos állapotokon keresztül jut el egy stabil állapotba.