A Hebb szabály biológiai eredetű eljárás [Heb49]. Legegyszerűbb formájában a következőképpen fogalmazható meg: két processzáló elem közötti kapcsolat erőssége (a processzáló elemek közötti súlytényező értéke) a processzáló elemek aktivitásának szorzatával arányosan változik.
, (10.1)
ahol
az i-edik és a j-edik processzáló elem közötti súly,
ill.
a két processzáló elem kimenetének értéke, μ pedig az eddigiekhez hasonlóan a tanulási tényező. Ha a súly egy bemenet és egy processzáló elem között található, ahol a bemenet értéke
, a processzáló elem kimenetének értéke pedig
, akkor a súlymódosítás értelemszerűen:
(10.2)
Az eredeti Hebb tanulási szabálynak különböző változatait dolgozták ki. Ezen változatok legfontosabb jellemzője, hogy a szabályba beépítettek egy normalizáló eljárást is, ugyanis az eredeti Hebb szabály mellett a súlyok minden határon túl növekedhetnek. A normalizálásnak több módjával találkozhatunk, melyeket az egyes nemellenőrzött tanítású hálózatok bemutatásánál fogunk tárgyalni.
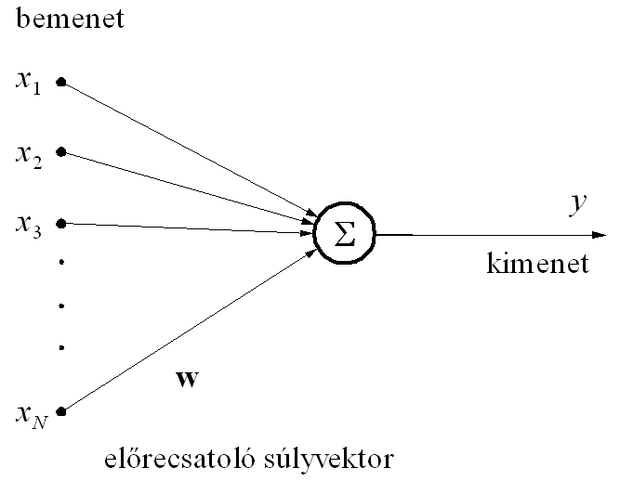
A nemellenőrzött tanítású hálók többnyire lineáris neuronokbólépülnek fel. Egy ilyen lineáris neuront mutat a 10.1 ábra, ahol a neuron kimenete a bemenetek súlyozott összegeként áll elő:
(10.3)
Megmutatható, hogy egy lineáris processzáló elem súlyainak Hebb szabály alapján történő módosítása azt eredményezi, hogy a processzáló elem kimenetének varianciája, vagyis
(10.4)
maximumot vesz fel azzal a feltétellel, hogy
(10.5)
Ez utóbbi feltétel vagy valamilyen normalizáló eljárással, vagy a súlyokra vonatkozó telítési feltétel beépítésével biztosítható.
Bizonyos hálózatoknál alkalmazzák az ún. anti-Hebb tanulásiszabályt is, amelynél − hasonlóan a Hebb szabályhoz − a súlymódosítás most is a bemenet és a kimenet aktivitásának szorzatával arányos, csak negatív előjellel:
. (10.6)
Az anti-Hebb szabály − szemben a Hebb szabály kimeneti variancia-maximumra törekvő hatásával − a kimeneti variancia minimumát igyekszik biztosítani. A súlymódosítás mindkét esetben a két aktivitás közötti korrelációval arányos, csak a változtatás iránya eltérő. A Hebb- és az anti-Hebb szabályok együttes alkalmazásának fontos szerepe van az ún. főkomponens meghatározó hálózatoknál; szerepüket részletesebben ezen hálózatok ismertetésénél mutatjuk be.
A versengő tanulása nemellenőrzött tanulások csoportjába tartozó másik eljárás, amelynek a célja, hogy egy neuronhálónál a neuronok közül egy győztest válasszunk ki. A győztes neuron kimenete aktív lesz, (bináris kimenet mellett a kimenet értéke 1 lesz), miközben az összes többi neuron passzív marad (bináris kimenet mellett mindegyik 0 értéket vesz fel). A versengő tanulás célja általában a bemeneti mintatér olyan tartományokra osztása, szegmentálása, hogy egy adott tartományba tartozó bemenet hatására egy és csakis egy processzáló elem aktivizálódjon. Az eljárás tehát egyfajta klaszterkialakítást eredményez.
A versengő tanulás tulajdonképpen két lépésből áll. Az első lépés során a neuronokból álló elrendezés minden processzáló elemének kimenetét meghatározzuk az aktuális súlyvektorok felhasználásával. Ezt követi a győztes kiválasztása, amely a "győztes mindent visz" (winner-takes-all) elv alapján működik. A tényleges tanulás, vagyis a súlyvektor módosítása csak a győztes kiválasztása után lehetséges, ugyanis a versengő tanulásnál csupán a győztes processzáló elem súlyvektorát (vagy a győztes valamely környezetében található processzáló elemek súlyvektorait) módosítjuk. Meg kell jegyeznünk, hogy a súlymódosítás a versengő tanulásnál is általában a Hebb szabállyal történik. A versengő tanulásnál a versengés során tehát valójában tanulás nincs is. A versengés arra szolgál, hogy kiválaszthassuk azt a neuront, melynek a súlyait valamilyen súlymódosító eljárással majd módosítani fogjuk.
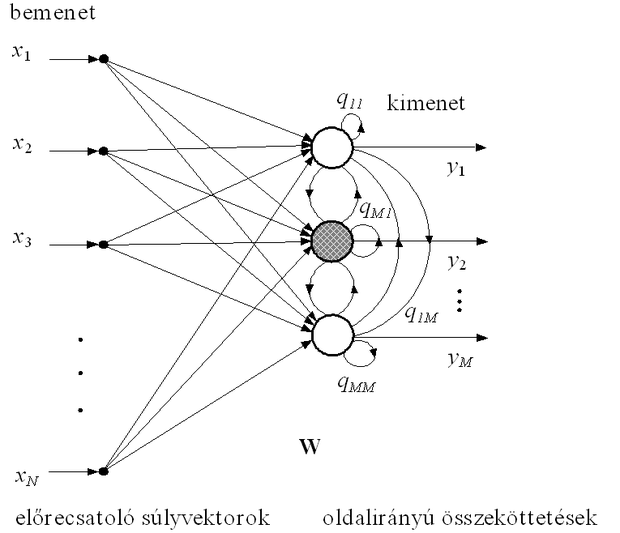
A győztes elem kiválasztása többféleképpen történhet. Triviális megoldás, ha kiszámítjuk egy adott bemenetre az összes processzáló elem kimenetét, és a legnagyobb kimenettel rendelkező PE, a győztes értékét 1-re állítjuk, az összes többiét pedig nullázzuk. A győztes kiválasztása azonban történhet "automatikusan" is, amikor a processzáló elemek között qij oldalirányú kapcsolatok vannak (ld. 10.2 ábra), és ezen kapcsolatokat megvalósító súlyok megfelelő kialakítása (és a kimeneten megfelelő nemlineáris aktivációs függvény alkalmazása) biztosítja, hogy a győztes (az ábrán az árnyékolt elem) kimeneti értéke 1, az összes többié pedig nulla lesz.
Az oldalirányú kapcsolatok súlytényezői rögzítettek: a közeli processzáló elemek között gerjesztő kapcsolat, a távolabbiak között gátló kapcsolat van.