9.3. Moduláris háló kialakítása a tanító mintakészlet módosításával

Az eddigi moduláris háló kialakításoknál akár dekomponáltuk a feladatot, akár a teljes feladatot oldottuk meg különböző hálókkal, minden esetben az eredeti tanítókészlettel vagy annak a dekompozícióhoz tartozó adott részhalmazával dolgoztunk. A következőkben olyan moduláris háló konstrukciókkal foglalkozunk, ahol az egyes modulokat tudatosan eltérő eloszlású adatkészletekkel tanítjuk, miközben továbbra is minden tanítópontunk az eredeti megoldandó problémából származik, bármelyik adatkészletről van is szó.

A tanító mintakészlet módosításával létrehozott moduláris hálóknál több hálót tanítunk és minden hálóhoz más-más eloszlású tanítókészletet használunk. A tanítókészlet módosításának legkézenfekvőbb módja az ún. bagging[8] eljárás. A bagging eljárás olyan hálókat hoz létre, melyeket az eredeti tanítókészletből véletlenszerű válogatással létrehozott mintakészletekkel tanítunk. Minden egyes újabb hálóhoz létre kell hoznunk egy új tanítókészletet, melynek elemszáma megegyezik az eredeti mintakészlet elemszámával és amelyet az eredeti mintakészletből visszatevéses mintavételezéssel hozunk létre. Az így létrehozott mintakészleteket az eredeti készlet bootstrap másolatainak, az egész technikát pedig bootstrap aggregálásnak nevezzük. A bootstrap másolatokra jellemző, hogy az eredeti mintakészletből egyes minták többször is előfordulhatnak benne, míg más minták teljes mértékben kimaradnak. A bootstrap másolatok átlagosan az eredeti mintakészlet 63,2%-át tartalmazzák [Bre96]. A bagging így az egyes hálók tanításához az eredetitől eltérő eloszlású mintakészleteket használ fel.

Az eredeti mintakészletből eltérő eloszlású mintakészletek előállításának további fontos lehetőségét jelentik a boosting eljárások [Scha02]. A boosting valójában fokozást jelent, ami itt arra utal, hogy a boosting eljárás eredményeképpen kapott moduláris háló jobb teljesítményre képes, mint ha az eredeti tanítókészlettel egyetlen hálót hoztunk volna létre. A boosting eljárások tehát a teljesítőképesség javítása érdekében módosítják a tanítókészletek eloszlását. A következőkben a legfontosabb boosting eljárásokat foglaljuk össze, és kitérünk annak rövid bemutatására is, hogy milyen mechanizmus áll a boosting eljárások teljesítőképesség-javító hatása mögött.

9.3.1. Boosting

Az előzőek alapján látható, hogy a boosting eljárások lényege, hogy a rendelkezésre álló tanítókészlet mintáinak a felhasználásával eltérő eloszlású mintakészleteket hozunk létre azzal a céllal, hogy az így kialakított mintakészletekkel különálló hálókat konstruáljunk. Az eredő megoldás itt is az egyes hálók eredményeinek valamilyen egyesítése útján nyerhető. A boosting eljárások tehát szintén moduláris hálóarchitektúrát eredményeznek, azonban az eddigi moduláris háló-konstrukcióktól lényegesen eltérő módon. A boosting eljárások az egyes modulok tanításához szükséges különböző eloszlású mintakészleteket szűréssel vagy az egyes minták tanítókészleten belüli szerepének módosításával állítják össze. A boosting eljárások osztályozós feladatok megoldására alkalmas moduláris architektúrákat eredményeznek.

Boosting szűréssel

A szűréssel történő boostingeljárás [Scha90] eredményeképpen egy három hálóból álló moduláris architektúrát kapunk, ahol a három háló tanítása három eltérő, de azonos (L) számú mintából álló tanítókészlettel történik. Az eljárás feltételezi, hogy nagyszámú tanítópont áll a rendelkezésünkre, mely mintakészletből az alábbi eljárás során hozzuk létre a három tanítókészletet:

  1. A rendelkezésre álló tanítómintákból válasszunk ki véletlenszerűen L mintapontot, és ezzel a tanítókészlettel tanítsuk meg az első hálót.

  2. A megtanított első háló felhasználásával szűrjünk ki a rendelkezésre álló és az első készletben fel nem használt mintakészletből újabb L pontot a következő eljárással:

  • Generáljunk azonos valószínűséggel 0-t vagy 1-et, vagyis dobjunk fel egy érmét.

  • Ha az eredmény fej (0), vegyünk elő egymás után újabb mintákat, és dolgozzuk fel ezeket a mintákat az első hálóval. Ha egy mintát az első háló helyesen osztályoz, akkor ezt a mintát dobjuk el, sőt dobjuk el a sorban elővett mintákat mindaddig, amíg egy hibásan osztályozott mintához nem érünk. Ezt a tévesen osztályozott mintát adjuk a második háló tanítókészletéhez.

  • Ha az eredmény írás (1), az előzővel ellentétesen kell cselekednünk. Vegyünk elő ismét egymás után újabb mintákat, és nézzük meg ezekre az első háló válaszát. Ha a válasz hibás, a mintát dobjuk el, sőt dobjuk el a további egymást követő mintákat is mindaddig, amíg egy helyesen osztályozott mintát nem kapunk. Most ezt a helyesen osztályozott mintát adjuk a második tanítókészlethez.

  • Folytassuk az eljárást, amíg L számú tanítópontot össze nem gyűjtünk. Az így létrehozott készlet képezi a második háló tanítóhalmazát.

Ez a mintapontválogató eljárás biztosítja, hogy a második mintakészletet az első háló 50%-os hibával osztályozza, tehát a második tanítóhalmaz eloszlása biztosan más lesz, mint az első háló tanításához használt mintakészleté.

A második háló megtanítása után alakítsunk ki egy harmadik tanítókészletet. Ehhez új pontokat vegyünk elő a kiinduló mintakészletből és nézzük meg ezekre a pontokra az első két háló válaszát.

  • Ha a két háló válasza megegyezik, a mintapontot dobjuk el. Ha a válaszok különböznek, a mintát tartsuk meg és adjuk a harmadik tanítókészlethez.

  • Folytassuk a válogató eljárást, amíg L pontot össze nem gyűjtöttünk.

Tanítsuk meg a harmadik hálót az így kapott készlettel.

A három hálóból képezzünk egy moduláris hálóegyüttest, ahol az eredő választ egyszerű szavazással nyerhetjük. Az eredmények aggregálásának más módját is javasolták [Dru93]. E szerint a javaslat szerint adjuk össze az egyes hálók kimeneteit (vegyük figyelembe, hogy a hálók kimenetei nem feltétlenül binárisak, hanem a [0,1] zárt intervallumban tetszőleges értéket felvehetnek) és az összeg alapján hozzuk meg az eredő osztálybasorolást. Ez utóbbi változat előnyét gyakorlati vizsgálatok támasztják alá.

A szűréssel dolgozó boosting eljárás hátránya, hogy igen sok tanítópontot igényel. Jelölje rendre L1, L2 és L3 az első, a második és a harmadik háló tanítókészletének kiválogatásához felhasznált tanítópontok számát. Az első hálónál ki kell választanunk véletlenszerűen L tanítópontot, tehát L1=L. A második és a harmadik tanítókészlethez viszont L-nél sokkal több pontra van szükségünk, hiszen a szűrési szabály szerint bizonyos pontokat el kell dobnunk. Ebből adódóan általában mind L2, mind L3 jóval nagyobb lesz, mint L, vagyis a három L-elemű tanítókészlethez Ltotal-elemű mintakészletből kell kiindulnunk, ahol általában Ltotal >>3L. Ha a kiinduló mintapontok (ismert válaszú pontok) száma korlátozott, akkor a megfelelő mintaszámú három tanítókészlet kiválogatása nehézségekbe ütközhet.

A nagy kiinduló mintapontszámra elsősorban azért van szükség, mert a tanítókészletek nem tartalmaznak közös mintapontokat. A következőkben bemutatandó AdaBoost eljárás ezt a hátrányt kiküszöböli, sokkal hatékonyabban használja föl a kiinduló mintakészletet, így összességében jóval kevesebb mintával is tud dolgozni.

AdaBoost

Az AdaBoosteljárás [Scha99] a mintapontok újtramintavételezésével biztosítja a tanítópontkészlet eloszlásának módosítását. A legfontosabb különbség az előzőekben bemutatott mintaszűréssel dolgozó boosting eljáráshoz képest, hogy megengedi a mintapontok újra felhasználását. Valójában az egyes tanítópontoknak az egyes hálók tanításánál betöltött szerepét változtatjuk.

Az eljárás bemutatásához induljunk ki abból, hogy rendelkezésünkre áll egy Z= { z l } l=1 L = { ( x l , d l ) } l=1 L MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqi=G0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOwaiabg2da9maacmaabaGaaCOEamaaDaaaleaacaWGSbaabaaaaaGccaGL7bGaayzFaaWaa0baaSqaaiaadYgacqGH9aqpcaaIXaaabaGaamitaaaakiabg2da9maacmaabaWaaeWaaeaacaWH4bWaaSbaaSqaaiaadYgaaeqaaOGaaiilaiaadsgadaWgaaWcbaGaamiBaaqabaaakiaawIcacaGLPaaaaiaawUhacaGL9baadaqhaaWcbaGaamiBaiabg2da9iaaigdaaeaacaWGmbaaaaaa@4CBC@ tanítókészlet, ahol feltesszük, hogy a dl kívánt válaszok a {−1, + 1} értékkészletből vehetnek fel értékeket, vagyis kétosztályos osztályozási problémával állunk szemben. A mintakészletben a tanítópontok valamilyen eloszlásnak megfelelően fordulnak elő. Az AdaBoost eljárás a tanítópontok eloszlását – az eredeti tanítópontoknak az adott mintahalmazban való előforulási gyakoriságát - változtatja adaptív módon. Innen ered az eljárás elnevezése is. Az eljárás iteratív módon működik: minden iterációban egy új tanuló rendszert (neuronhálót) hozunk létre egy módosított eloszlású tanítókészlettel. (Megjegyezzük, hogy az AdaBoost eljárás és az egyéb boosting eljárások általános mintaeloszlás-módosító eljárások, tehát nemcsak neuronhálóknál alkalmazhatók. Ennek ellenére most feltételezzük, hogy az eljárást moduláris háló kialakításához alkalmazzuk.)

Jelölje a t-edik iterációban az l-edik mintának a tanítókészleten belüli előfordulási gyakoriságát Dt(l). Kiinduláskor ez minden tanítópontra azonos, vagyis D1(l)=1/L, minden l=1,2,…,L-re. (Tehát minden egyes minta egyszer fordul elő az L elemű halmazban.) Az egymást követő iterációkban az egyes mintapontok előfordulási gyakoriságát módosítjuk: a helytelenül osztályozott minták gyakoriságát növeljük, a helyesen osztályozottakét csökkentjük. Ez azt eredményezi, hogy arra kényszerítjük a következő iterációban az újabb osztályozót, hogy a nehéz esetekkel többet foglalkozzon.

Az algoritmus lépései a t=1,…,T iteráció során a következők:

1. Tanítsunk meg egy hálót a Dt eloszlású mintakészlettel.

2. Minősítsük a megtanított hálót az alábbi hibadefiníció alapján:

ε t =P{ y t ( x l )≠ d l } MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqi=G0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aaSbaaSqaaiaadshaaeqaaOGaeyypa0JaamiuamaacmaabaGaamyEamaaBaaaleaacaWG0baabeaakmaabmaabaGaaCiEamaaBaaaleaacaWGSbaabeaaaOGaayjkaiaawMcaaiabgcMi5kaadsgadaWgaaWcbaGaamiBaaqabaaakiaawUhacaGL9baaaaa@4600@ (9.46)

ahol yt(xl) a t-edik iterációban alkalmazott háló válasza xl bemenetre. A hiba fenti kifejezése annak a valószínűségét adja meg, hogy a t-edik háló az l-edik mintát hibásan osztályozza. A hibavalószínűség a mintapontok előfordulási gyakoriságával is kifejezhető:

ε t = ∑ l: y t ( x l )≠ d l D t ( l ) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqi=G0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aaSbaaSqaaiaadshaaeqaaOGaeyypa0ZaaabuaeaacaWGebWaaSbaaSqaaiaadshaaeqaaOWaaeWaaeaacaWGSbaacaGLOaGaayzkaaaaleaacaWGSbGaaiOoaiaadMhadaWgaaadbaGaamiDaaqabaWcdaqadaqaaiaahIhadaWgaaadbaGaamiBaaqabaaaliaawIcacaGLPaaacqGHGjsUcaWGKbWaaSbaaWqaaiaadYgaaeqaaaWcbeqdcqGHris5aaaa@4B44@ (9.47)

3. Válasszunk egy αt együtthatót a következőképpen

α t = 1 2 ln( 1− ε t ε t ) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqi=G0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySde2aaSbaaSqaaiaadshaaeqaaOGaeyypa0ZaaSaaaeaacaaIXaaabaGaaGOmaaaacaqGSbGaaeOBamaabmaabaWaaSaaaeaacaaIXaGaeyOeI0IaeqyTdu2aaSbaaSqaaiaadshaaeqaaaGcbaGaeqyTdu2aaSbaaSqaaiaadshaaeqaaaaaaOGaayjkaiaawMcaaaaa@4591@ (9.48)

4. Frissítsük a mintapontok eloszlását (módosítsuk a mintapontok előfordulási gyakoriságát) az alábbiak szerint:

D t+1 ( l )= D t ( l ) S t ×{ e − α t     ha  y t ( x l )= d l e α t       ha  y t ( x l )≠ d l                                   = D t ( l ) exp( − α t d l y t ( x l ) ) S t MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqi=G0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGebWaaSbaaSqaaiaadshacqGHRaWkcaaIXaaabeaakmaabmaabaGaamiBaaGaayjkaiaawMcaaiabg2da9maalaaabaGaamiramaaBaaaleaacaWG0baabeaakmaabmaabaGaamiBaaGaayjkaiaawMcaaaqaaiaadofadaWgaaWcbaGaamiDaaqabaaaaOGaey41aq7aaiqaaeaafaqabeGabaaabaGaamyzamaaCaaaleqabaGaeyOeI0IaeqySde2aaSbaaWqaaiaadshaaeqaaaaakiaabccacaqGGaGaaeiiaiaabccacaqGObGaaeyyaiaabccacaWG5bWaaSbaaSqaaiaadshaaeqaaOWaaeWaaeaacaWH4bWaaSbaaSqaaiaadYgaaeqaaaGccaGLOaGaayzkaaGaeyypa0JaamizamaaBaaaleaacaWGSbaabeaaaOqaaiaadwgadaahaaWcbeqaaiabeg7aHnaaBaaameaacaWG0baabeaaaaGccaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGObGaaeyyaiaabccacaWG5bWaaSbaaSqaaiaadshaaeqaaOWaaeWaaeaacaWH4bWaaSbaaSqaaiaadYgaaeqaaaGccaGLOaGaayzkaaGaeyiyIKRaamizamaaBaaaleaacaWGSbaabeaaaaaakiaawUhaaaqaaiaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaaGjcVlaayIW7caaMi8UaaGjcVlaayIW7cqGH9aqpdaWcaaqaaiaadseadaWgaaWcbaGaamiDaaqabaGcdaqadaqaaiaadYgaaiaawIcacaGLPaaacaqGGaGaaeyzaiaabIhacaqGWbWaaeWaaeaacqGHsislcqaHXoqydaWgaaWcbaGaamiDaaqabaGccaWGKbWaaSbaaSqaaiaadYgaaeqaaOGaamyEamaaBaaaleaacaWG0baabeaakmaabmaabaGaaCiEamaaBaaaleaacaWGSbaabeaaaOGaayjkaiaawMcaaaGaayjkaiaawMcaaaqaaiaadofadaWgaaWcbaGaamiDaaqabaaaaaaaaa@BA62@ (9.49)

ahol St egy normalizáló tényező, melyet úgy kell megválasztani, hogy Dt+1 egy diszkét valószínűség-sűrűségfüggvény legyen, tehát ∑ l D t+1 (l) =1 MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqi=G0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabeaeaacaWGebWaaSbaaSqaaiaadshacqGHRaWkcaaIXaaabeaakiaacIcacaWGSbGaaiykaaWcbaGaamiBaaqab0GaeyyeIuoakiabg2da9iaaigdaaaa@3FE8@ .

5. Amennyiben nem értük még el az iteráció leállási feltételét (kielégítő pontosságot, adott iterációszámot vagy más feltételt), akkor növeljük t-t eggyel és lépjünk az 1. lépésre. Ha az iteráció végére értünk (T lépés után), akkor hozzuk létre az eredő osztályozót:

6. Az eredő választ a következőképpen határozzuk meg:

y( x )=sign( ∑ t=1 T α t y t ( x ) ) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqi=G0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaabmaabaGaaCiEaaGaayjkaiaawMcaaiabg2da9iaabohacaqGPbGaae4zaiaab6gadaqadaqaamaaqahabaGaeqySde2aaSbaaSqaaiaadshaaeqaaOGaamyEamaaBaaaleaacaWG0baabeaakmaabmaabaGaaCiEaaGaayjkaiaawMcaaaWcbaGaamiDaiabg2da9iaaigdaaeaacaWGubaaniabggHiLdaakiaawIcacaGLPaaaaaa@4CA1@ (9.50)

Láthatóan az algoritmus során egymást követően több hálót konstruálunk, mindegyiket egy valamilyen mértékben módosított tanítókészlettel. Mind a tanítókészlet módosításához, mind a részeredmények aggregálásához felhasználunk egy αt együtthatót, ami a t-edik háló fontosságának mértékeként is tekinthető. Vegyük észre, hogy αt ≥ 0, ha εt ≤ 1/2, és αt egyre nagyobb lesz, ha εt csökken. Az εt ≤ 1/2 nem tekinthető megszorításnak, hiszen bármilyen osztályozó konstruálásánál nyilvánvaló követelmény, hogy az osztályozási hiba nem haladhatja meg az 50%-ot.

A mintapontok eloszlásának módosítását megadó (9.49) összefüggés szerint hibás osztályozás esetén növelni kell az adott mintapont szerepét a tanítókészletben és csökkenteni, ha az osztályozás helyes. Így a később létrehozott hálók egyre inkább a „nehéz” mintákra koncentrálnak. Az eredő választ az egyes hálók válaszainak súlyozott összegeként kapjuk, ahol a súlyozás szintén az αt együtthatókkal történik.

A fentiek alapján az AdaBoost eljárással konstruált moduláris háló beleillik a hálóegyüttesek sorába. Itt is különálló hálók lineáris kombinációjával nyerjük az eredményt, és a teljesítőképesség javulásának az esélyét az adja, hogy az egyes hálók különböző minőségben oldják meg a feladatot. Az eltérő minőségű megoldások alapját a tudatosan konstruált eltérő eloszlású tanítókészletek adják.

A boosting eljárások minősítése

A boosting eljárások teljesítőképesség-növelő hatása általánosan is vizsgálható. Ez a megközelítés a valószínűleg közelítőleg helyes(VKH) (probably approximately correct, PAC) tanulási modellen alapul. A valószínűleg közelítőleg helyes tanulási modell [Val84], [Rus05] a tanulás számítási elméletéhez kapcsolódik és bináris osztályozási feladatoknál a tanulás alapkérdésére keresi a választ: miért működik egyáltalán a mintákból történő tanulás?

A boosting eljárásokkal kapcsolatban a kérdés úgy merül fel, hogy egy olyan tanuló algoritmus, amelynek a teljesítőképessége az 50%-os találati aránynál (a véletlen választásnál) épp hogy csak jobb, feljavítható-e tetszőlegesen pontos tanuló eljárássá. Az olyan tanulást, amelynek eredménye az 50%-os találati arányt épp hogy meghaladja gyenge tanulásnak (weak learning), míg a tetszőlegesen kis hibát eredményező eljárást erős tanulásnak (strong learning) nevezzük. Kérdés tehát, hogy a gyenge tanulás feljavítható-e erős tanulássá. A válasz általánosan is pozitív, amit úgy fogalmazhatunk meg, hogy az erős és a gyenge tanulás ekvivalens fogalmak [Scha90], [Fre95], [Scha99].

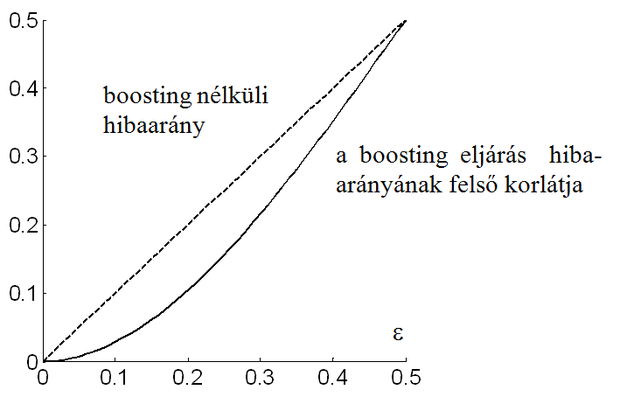
A szűréssel történő boosting eljárás hibacsökkentő hatását Schapire vizsgálta [Scha90]. E szerint, ha az eredeti hibaarány (a válogatás nélkül kapott mintakészlettel tanított első háló hibája) ε, a hálóegyüttes eredő hibájára a következő felső korlát érvényes:

g( ε )=3 ε 2 −2 ε 3 MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqi=G0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4zamaabmaabaGaeqyTdugacaGLOaGaayzkaaGaeyypa0JaaG4maiabew7aLnaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaikdacqaH1oqzdaahaaWcbeqaaiaaiodaaaaaaa@421C@ (9.51)

Látható, hogy g(ε) jóval kisebb is lehet, mint ε. Ezt mutatja a 9.8 ábra, ahol ε függvényében a folytonos vonal jelöli a fenti felső korlátot. Az ábra alapján az is nyilvánvaló, hogy ha rekurzív módon alkalmazzuk a mintaszűrő eljárást, az eredő hiba tetszőlegesen kicsivé tehető. A rekurzív alkalmazás azonban általában inkább csak elvi lehetőség, hiszen ez az amúgy is nagy kiinduló mintakészlet további növelését igényli.

9.8. ábra - A szűréssel történő boosting eljárás teljesítőképesség-javító hatása
A szűréssel történő boosting eljárás teljesítőképesség-javító hatása

Az AdaBoost eljárás teljesítőképesség-növelő hatásának elemzését Yoav Freund és Robert Schapire adták meg [Fre97]. E szerint ha a t-edik iterációban a (9.47) összefüggés szerinti hiba ε t =1/2− γ t MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqi=G0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aaSbaaSqaaiaadshaaeqaaOGaeyypa0JaaGymaiaac+cacaaIYaGaeyOeI0Iaeq4SdC2aaSbaaSqaaiaadshaaeqaaaaa@3F28@ , (γt > γ, ahol γ valamilyen kis pozitív konstans) akkor az eredő megoldás hibája a tanítópontokra legfeljebb:

∏ t 2 ε t ( 1− ε t ) = ∏ t 1−4 γ t 2 ≤exp( −2 ∑ t γ t 2 ) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqkLspG0dg9v8qqaqFD0xXdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaqeqbqaaiaaikdadaGcaaqaaiabew7aLnaaBaaaleaacaWG0baabeaakmaabmaabaGaaGymaiabgkHiTiabew7aLnaaBaaaleaacaWG0baabeaaaOGaayjkaiaawMcaaaWcbeaaaeaacaWG0baabeqdcqGHpis1aOGaeyypa0ZaaebuaeaadaGcaaqaaiaaigdacqGHsislcaaI0aGaeq4SdC2aa0baaSqaaiaadshaaeaacaaIYaaaaaqabaaabaGaamiDaaqab0Gaey4dIunakiabgsMiJkaabwgacaqG4bGaaeiCamaabmaabaGaeyOeI0IaaGOmamaaqafabaGaeq4SdC2aa0baaSqaaiaadshaaeaacaaIYaaaaaqaaiaadshaaeqaniabggHiLdaakiaawIcacaGLPaaaaaa@5E20@ (9.52)

Vagyis ha a gyenge tanulás bármilyen kismértékben, de jobb, mint a véletlen választás, az AdaBoost eljárással kapott eredő hiba exponenciálisan gyorsan csökken. A (9.52) összefüggés ugyanakkor csak a tanítópontokban meghatározott hibára vonatkozik és nem az általánosítási hibára.


[8] A bagging elnevezés a bootstrap aggregation elnevezésből született, ahol a bootstrap önerőből történő képességjavítást jelent. A bagging ezért olyan integrált megoldás, ahol különböző, külső segítség nélkül javított megoldásokból, azok egyesítése útján kapjuk az eredő megoldást.