9.2. Szakértőegyüttesek

9.2.1. Hálók optimális lineáris kombinációja

A hálók lineáris kombinációjának alapötletét az adta, hogy egy gyakorlati feladat megoldásánál szinte minden esetben több hálót konstruálunk, és ezek közül választjuk ki a legjobbat. Ennek alapvető oka, hogy az „optimális” hálót általában nem tudjuk megtervezni. Egy adott feladat megoldására alkalmas háló konstrukciójának nem minden lépését tudjuk a feladatból egyértelműen származtatni, így azt sem tudjuk általában eldönteni, hogy mit tekinthetünk optimális hálóarchitektúrának. Egy megfelelően jó megoldás eléréséhez ezért valójában több, esetenként meglehetősen sok, kisebb vagy nagyobb mértékben eltérő hálót hozunk létre. Ezek a hálók különbözhetnek a felépítésükben − akár eltérő hálótípusokkal (pl. MLP, RBF, SVM, stb.) is próbálkozhatunk −, de lehet, hogy csak a háló méretében vagy a tanítás módjában, esetleg a felhasznált tanítókészlet összeállításában van különbség. Ha csak a „legjobb” hálót tartjuk meg és a többit eldobjuk, akkor a „mellékeredményeket” csak részben hasznosítjuk. A mellékeredmények ugyanis nemcsak abból a szempontból tekinthetők fontosnak, hogy kialakításuk a végleges háló konstrukcióját segíti, hanem abból a szempontból is, hogy az egyes megoldások a teljes feladat bizonyos tartományain akár a végleges megoldásnál jobb eredményt is nyújthatnak. Ezt a „képességüket” is célszerű hasznosítani.

A hálók lineáris kombinációjánál több háló kimenetének súlyozott összegét képezzük [Has97]:

$\bar{y} (x, α) = \sum_{j = 0}^{M} α_{j} y_{j} (x)$ (9.10)

ahol az α_j , j=0, 1, …, M együtthatók a lineáris kombináció súlytényezői.

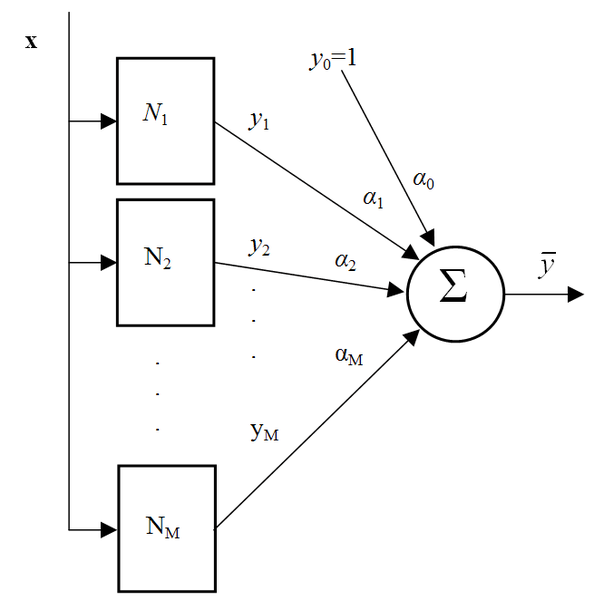
A teljes moduláris háló a 9.6 ábrán látható.

A hálóegyüttesben M modul található, a kimeneti súlyozott összegzésben pedig még egy eltolásérték (bias) is szerepel (y₀(x)≡1 és α₀képviseli az eltolásértéket). Az ábrából látható, hogy a hálók lineáris kombinációja úgy is tekinthető, mint egy olyan többrétegű háló, melynek az utolsó kimeneti rétege lineáris. Ha az egyes modulok MLP-k, akkor az egész moduláris kialakítás egy többrétegű perceptron. A moduláris kialakítás azonban egy általános többrétegű perceptronhoz képest több lényeges eltérést mutat. Egyrészt az egyes modulok kialakítása egymástól függetlenül történik, másrészt – ahogy ezt a továbbiakban látni fogjuk – a kimenő, integráló réteg súlyait nem a hagyományos módon és nem a modulok tanításával együtt tanítjuk.

Ha a hálóegyüttes kialakításánál a fenti gondolatmenetből indulunk ki, akkor hálók lineáris kombinációjánál különállóan megtanított hálókból építjük fel a moduláris hálót. Ez azt jelenti, hogy az egyedi hálók tanításán túl további feladatokat kell megoldani. Meg kell határozni, hogy hány modulból álljon a moduláris rendszer és azt is, hogy a rendelkezésre álló egyedi hálók közül melyek kerüljenek kiválasztásra, majd meg kell határozni a lineáris kombináció súlyait.

9.6. ábra - Hálók lineáris kombinációja több-bemenetű − egykimenetű esetben

Az egyedi hálók kiválasztása

Az egyedi hálók számának meghatározására nincs általános módszer. A hálóegyüttes létrehozásának elsődleges célja a megoldás minőségének javítása, így csak a teljes moduláris háló kiértékelése alapján dönthetjük el, hogy adott számú modulból felépülő hálóegyüttes egy adott feladat megoldása szempontjából megfelelő-e vagy sem. Egyfelől azt mondhatjuk, hogy a modulok számának növelése a teljes rendszer általánosítóképességét várhatóan javítja, másfelől a túl sok modul túl sok erőforrást igényel, ami az alkalmazás korlátja is lehet.

Az általánosítóképesség javulását intuitíve a kimeneti súlyozott összegző átlagoló hatásával magyarázhatjuk, másrészt a következő alfejezetben − legalábbis bizonyos speciális súlyozás esetére − formálisan is alátámasztjuk. A túl sok modul összességében túl sok szabad paramétert jelent, és − amint ezt az előző fejezetekben láttuk − a túl sok szabad paraméter általában túlilleszkedésre vezethet. A túlilleszkedés veszélye a hálóegyüttesnél azonban nem jelentős, hiszen itt olyan modulok összekapcsolásáról van szó, melyeket külön-külön alakítottunk ki, így ha ezek a modulok önmagukban nem mutatnak túlilleszkedési hajlamot, akkor ez a veszély a súlyozott összegükre sem áll fenn. Másfelől hálóegyütteseknél az egyedi hálóknál jelentkező túlilleszkedés még előnyös is lehet, ahogy erre a következőkben utalni fogunk.

A modulok számára korlátot inkább az jelent, hogy az egyes modulok mennyiben hoznak új eredményt, illetve milyen kapcsolat van az egyes modulok válaszai között. Ha két vagy több modul kimenetei lineárisan összefüggők, akkor a moduláris kiépítés redundáns, ráadásul az ilyen helyzet az integráló réteg súlyainak meghatározását is nehezíti.

Az integráló réteg súlyainak meghatározása

A kimeneti réteg súlyait leggyakrabban a kimeneti átlagos négyzetes hiba minimalizálása útján határozzuk meg. Ekkor – mivel a modulokat integráló réteg szempontjából az egyes modulok kimenetei lesznek a bemenetek – a súlyozó hálózat nem más, mint egy adaline, melynek optimális súlyait a Wiener-Hopf egyenlet alapján határozhatjuk meg. E szerint:

$α^{*} = R_{y y}^{- 1} p .$ (9.11)

ahol

$R_{y y}^{} = E {y y^{T}}$ és $p = E {d y}$ (9.12)

a modulok kimeneteiből képzett vektornak ( $y = {[y_{1}, y_{2}, \dots, y_{M}]}^{T}$ ) autokorrelációs mátrixa, illetve a modulok kimeneteinek és a kívánt kimenetnek a keresztkorrelációs vektora. A megoldáshoz az $R_{y y}$ mátrix becslésére és a mátrix inverzének a kiszámítására van szükség.

A súlyok optimális értékének meghatározása után a következőkben arra keressük a választ, hogy az optimális lineáris kombináció eredményeképp kapott hálóegyüttessel milyen eredmény érhető el. Több hálóból álló hálóegyüttes alkalmazásának ugyanis csak akkor van értelme, ha eredőben jobb eredményt érhetünk el, mint amit bármelyik egyedi háló elérne.

9.2.2. Pontos és különböző szakértők együttese

Hálóegyüttesnél az egyes hálók által szolgáltatott megoldásoknak valamilyen mértékben különbözniük kell egymástól, ugyanis azonos eredmények bármilyen súlyokkal történő súlyozott összegeként is csak ezt az azonos választ kaphatjuk. Eltérő válaszok azonban lehetőséget adnak arra, hogy az egyedi válaszok kombinálásaként az egyes válaszok egymást segítve, egymást kiegészítve, összességében a teljes feladatra nézve jobb megoldást szolgáltassanak, mint bármelyik egyedi megoldás. A hálóegyüttes alkalmazásának kulcseleme tehát az egyedi megoldások különbözősége. A következőkben ezt a kérdést próbáljuk egy kicsit részletesebben megvizsgálni.

Egy hálóegyüttes vizsgálatánál induljunk ki abból, hogy van M hálónk, melyek mindegyike a teljes feladatot oldja meg. Jelöljük ezeknek a hálóknak a kimenetét adott x bemenet mellett y_j(x)-szel (j=1,2,…,M). A hálóegyüttes kimenetét az előző részben alkalmazott eljáráshoz hasonlóan az egyes hálók kimeneteinek súlyozott összegeként határozzuk meg. Jelöljük $\overset{⇀}{y}$ (x,α)-val az eredő választ, hiszen a súlyozott kimenet nemcsak az x bemenetnek hanem az α_j súlyoknak is a függvénye:

$\bar{y} (x, α) = \sum_{j = 1}^{M} α_{j} y_{j} (x)$ (9.13)

A következőkben – az előző részben alkalmazott megoldástól eltérően – kikötjük, hogy a súlyok legyenek pozitívak és összegük legyen egységnyi, vagyis teljesüljenek a

$\sum_{j = 1}^{M} α_{j} = 1$ és $α_{j} > 0 j = 1,2, \dots, M$ (9.14)

feltételek. Ez a kikötés fontos lesz a továbbiakban.

A hálóegyüttes minősítéséhez meg kell határozni az eredő válasz hibáját. Amennyiben most is négyzetes hibakritériumot alkalmazunk, adott mintapontban az eredő válasz hibáját

$e (x) = ε^{2} (x) = [d (x) - \bar{y} (x, α)]^{2}$ (9.15)

adja meg. Az eredő hiba mellett meghatározhatjuk az egyes egyedi megoldások négyzetes hibáit is. A j-edik modul hibája ennek megfelelően:

$e_{j} (x) = ε_{j}^{2} (x) = [d (x) - y_{j} (x)]^{2}$ (9.16)

Minthogy az egyes megoldások különbözni fognak egymástól, célszerű, ha meghatározzuk az egyes megoldásoknak az eredő megoldástól való négyzetes eltérését, különbözőségét is. Jelöljük ezt a(x)-szel. (A jelölés az angol ambiguity elnevezésre utal, mely elnevezést itt a különbözőség megjelölésére használunk.)

$a_{j} (x) = [y_{j} (x) - \bar{y} (x, α)]^{2}$ (9.17)

Az egész hálóegyüttesre értelmezhetünk egy eredő különbözőséget, mint az egyes hálókra számított különbözőségek súlyozott összegét:

$\bar{a} (x, α) = \sum_{j = 1}^{M} α_{j} a_{j} (x) = \sum_{j = 1}^{M} α_{j} [y_{j} (x) - \bar{y} (x, α)]^{2}$ (9.18)

Látható, hogy az eredő különbözőség egy súlyozott variancia jellegű mennyiség.

Ha az egyedi hibák súlyozott átlagát az alábbi összefüggés szerint definiáljuk

$\bar{e} (x, α) = \sum_{j = 1}^{M} α_{j} e_{j} (x)$ , (9.19)

a hálóegyüttes eredő válaszának négyzetes hibája a következő formában is felírható:

$e (x) = [d (x) - \bar{y} (x, α)]^{2} = \bar{e} (x, α) - \bar{a} (x, α)$ (9.20)

Az eddigi összefüggések által meghatározott mennyiségek adott x bemenet mellett jellemezték az egyedi hálózatokat illetve a hálóegyüttest. Az összes lehetséges bementre integrálva a fenti összefüggéseket meghatározhatjuk a teljes feladatra is az eredő hibát, az egyedi hibák súlyozott átlagát és a különbözőségek súlyozott átlagát.

$E = \int_{x} e (x, α) p (x) d x$ (9.21)

$\bar{E} = \int_{x} \bar{e} (x, α) p (x) d x$ (9.22)

$\bar{A} = \int_{x} \bar{a} (x, α) p (x) d x$ (9.23)

Ennek alapján a hálóegyüttes általánosítási hibájára is érvényes az egy mintapontra meghatározott (9.20) összefüggés megfelelője.

$E = \bar{E} - \bar{A}$ (9.24)

A (9.24) összefüggés fontos jellemzője, hogy ebben szétválasztva szerepel az egyes hálók általánosítási hibáitól függő tag és a hálók válaszai közötti korrelációtól függő tag. Az első tag ugyanis az egyes hálók hibáitól függ, tehát ebben a tagban szerepet kapnak a hálóknak a kívánt választól való eltérései, míg a második tag anélkül is meghatározható, hogy ismernénk a kívánt válaszokat. A (9.24) összefüggés a torzítás-variancia dilemma (ld. 2. fejezet) egyfajta megfogalmazásának is tekinthető. Ugyanis, ha a hálóegyüttes válasza torzított, ez arra utal, hogy a különálló válaszok meglehetősen hasonlóak (és torzítottak is) még azokra a bemenetekre is, melyeket nem használtunk fel a tanításnál. Ilyenkor az eredő megoldás általánosítási hibája alapvetően meg fog egyezni az egyes megoldások általánosítási hibáinak súlyozott összegével. Ha ugyanakkor a variancia nagy, vagyis az egyes megoldások jelentős mértékben eltérnek egymástól, az eredő megoldás általánosítási hibája kisebb lehet, mint az általánosítási hibák súlyozott összege. Általánosságban is igaz, hogy

$E \leq \frac{1}{M} \sum_{j = 1}^{M} E_{j}$ (9.25)

ahol a j-edik háló teljes hibája

$E_{j} = \int_{x} e_{j} (x) p (x) d x$ (9.26)

Az előbbiekből közvetlenül következik, hogy az eredő hiba úgy redukálható, ha az egyes hálók válaszai minél inkább különböznek, vagyis a (9.24) egyenletben a második tag egyre nagyobb, feltéve, ha közben biztosítani tudjuk, hogy az első tag ne növekedjen. Az eredő válasz négyzetes hibájának felírásából látható, hogy a négyzetes kifejezés miatt az semmiképp nem fordulhat elő, hogy (9.24) negatív eredményt adjon, bármekkora is a különbözőség az egyes különálló válaszok között.

A (9.24) összefüggés az ún. pontos és különböző (accurate and diverse) elv megfogalmazásának az alapja [Kro95], [Sol96]. Ennek megfelelően egy hálóegyüttes kialakításánál arra kell törekedni, hogy az egyes megoldások külön-külön minél pontosabbak és egymástól minél inkább eltérőek legyenek.

A különböző, de pontos eredmények elérésének számos módja van. Általában különböző hálótípusokat alkalmazhatunk, vagy ha az összes háló azonos típusú, akkor a hálók méretében vagy a tanítókészlet összeállításában, esetleg a tanítás módjában lehet különbség. Különböző megoldást kaphatunk akkor is, ha eltérő kezdeti értékeket alkalmazunk.

A hálóegyütteseknél a túlilleszkedés − amit az egyedi hálók esetében hátrányként említettünk − még előnyös is lehet. Ez azt jelenti, hogy a regularizáció szerepe, mely a túltanulás veszélyét hivatott mérsékelni itt kevésbé fontos.

Bár az eddigiekben mindig hálóegyüttesről beszéltünk, egy moduláris rendszer létrehozásánál az egyes megoldások akár eltérő megközelítés alkalmazásával is születhetnek. Például neuronhálós megoldások mellett fuzzy, szabályalapú, vagy más alapokon nyugvó megoldások együttesét is kialakíthatjuk. Ilyenkor hálóegyüttes helyett inkább szakértőegyüttesről beszélhetünk.

9.2.3. MOE (Mixture Of Experts) architektúra

A MOE (Mixture Of Experts) [Jac91], [Jor94] architektúra egy olyan speciális hálóegyüttes (szakértőegyüttes), ahol az előbbiekben bemutatott hálóegyütteshez hasonlóan szintén az egyes hálók válaszainak súlyozott összegeként kapjuk az eredő választ, azonban itt a súlyokat nem rögzítjük, hanem egy ún. kapuzóhálózat kimenetén nyerjük. Ellentétben ugyanis az eddigiekben vizsgált hálóegyüttesektől, amelyekben a mintahalmazra adott válaszok alapján egy általánosan minden bemenet esetén használt (az adott feladatra konstans) súlykészletet határozunk meg, itt a súlyok közvetlenül függnek a bemenettől is. A kapuzóhálózat valójában maga is egy nemlineáris több-bemenetű−többkimenetű tanítható rendszer, mely bemenetként szintén a háló bemeneteit kapja, kimenetként pedig a súlyozó együtthatók értékeit, a kapuzóértékeket szolgáltatja.

A MOE specialitását részben épp ez a kapuzóhálózat adja, hiszen ennek kialakítása biztosítja, hogy az előzőekben tárgyalt hálóegyüttestől eltérően itt a modulok kimeneteit nem fix súlyozással fogjuk össze, hanem bemenetfüggő kapuzóértékekkel. A bemenetfüggő súlyozás indítéka nyilvánvaló: feltételezhető, hogy az egyes szakértők a bemeneti tér különböző tartományain különböző minőségben oldják meg a feladatot, így, ha az egyes szakértőknek az eredő kimenethez való hozzájárulását a teljes feladatra azonos módon rögzítenénk, biztosan nem kapnánk optimális megoldást. Célszerűbb, ha megengedjük, hogy az egyes szakértők szerepe bemenetfüggő legyen, vagyis az eredő válaszhoz való hozzájárulásuk a problématér egyes tartományaiban kisebb, más tartományaiban pedig nagyobb legyen. A bemenetfüggő súlyozás a részeredmények rugalmas aggregálását teszi lehetővé, hiszen ebbe a keretbe belefér az is, ha a választ a szakértők válaszának egyszerű átlagaként kapjuk, és az is, ha egyes tartományokban az eredő választ csak egyetlen háló határozza meg.

A kapuzóértékek maguk is függvényei a bemenetnek, sőt a kapcsolat a bemenet és a kapuzóértékek között nemlineáris, ezért a MOE architektúra akkor is nemlineáris leképezést valósít meg, ha az egyes szakértők önmagukban lineárisak. A MOE architektúránál általában meg is engedjük, hogy az egyes szakértők egyszerű felépítésűek, pl. lineáris hálózatok legyenek. A továbbiakban azonban a bemenetek és a kimenetek között az általánosabb

$y_{i} = f (x, Θ_{i})$ i=1,2,…,M, (9.27)

kapcsolatot tételezünk fel, ami valamilyen statikus, lineáris vagy nemlineáris leképezést jelent, de dinamikus hálókból is képezhetünk szakértőegyüttest (ld. pl. [Zee97]). A (9.27) összefüggésben $Θ_{i}$ az i-edik szakértő paramétereit összefogó mátrixot jelöli.

A MOE hálózatnál minden szakértő a teljes feladatot oldja meg, így az eredmény az egyes modulok közötti versengés és együttműködés eredményeként születik meg.

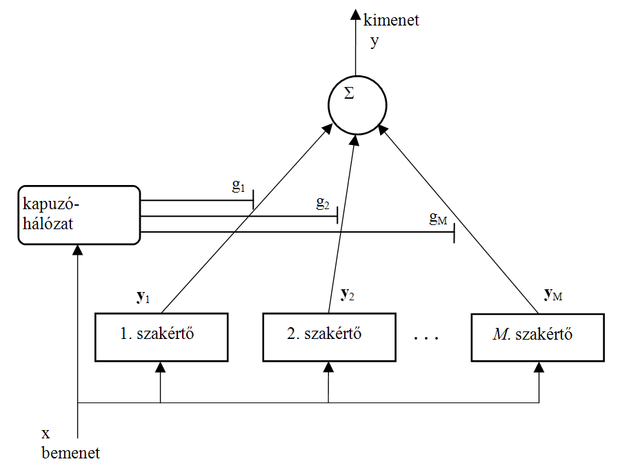
9.7. ábra - A MOE (Mixture of Experts) architektúra

A hálózat felépítését a 9.7 ábra mutatja. Az x bemenetet mindegyik szakértő (egyedi háló) és a kapuzó hálózat is megkapja. Az i-edik háló kimenetét y_i jelöli, míg y lesz a teljes hálóegyüttes kimenete. A súlyozott összeg képzéséhez a g_i súlyokat a kapuzóhálózat állítja elő.

A teljes szakértőegyüttes kimenete ennek megfelelően:

$y = \sum_{i = 1}^{M} g_{i} y_{i}$ . (9.28)

A többdimenziós kimenet (9.28) összefüggése azt jelzi, hogy a kimenet egyes komponenseinek azonos a súlyozása, tehát a kapuzóhálózatot nem komponensenként, hanem a teljes kimeneti vektorra együtt alkalmazzuk. A MOE architektúránál is kikötjük, hogy a g_i kapuzóértékekre teljesüljenek az alábbi feltételek:

$\sum_{i = 1}^{M} g_{i} = 1 és 0 \leq g_{i} \leq 1 i = 1, 2, \dots, M$ (9.29)

Ezeknek a feltételeknek a háló működésének valószínűségi értlemezésénél lesz szerepük.

A (9.29) feltételeknek eleget tevő kapuzóértékeket sokféleképpen elő lehet állítani. A MOE hálózatnál leggyakrabban az ún. „szoftmax” függvényt alkalmazzuk:

$g_{i} = \frac{e^{ξ_{i}}}{\sum_{j = 1}^{M} e^{ξ_{j}}}$ , (9.30)

ahol a ξ_i közbenső változót az x bemenővektor és egy v_i paramétervektor skalár szorzataként kapjuk: $ξ_{i} = v_{i}^{T} x$ .

A szoftmax függvény hatása valójában az lesz, hogy a MOE a bemeneti tartományt „lágyan” particionálja, olyan tartományokat határoz meg, melyekhez eltérő kapuzóértékek tartoznak, de amely tartományok határai általában elmosódottak. (A g_i értékek az i-edik szakértő esetén tipikusan egy tartományon dominánsak, közel 1 értékűek, de nem változnak meredeken sem 0→1, sem 1→0 irányban a tartomány határain.) A MOE architektúra ezért úgy is felfogható, mintha a feladatot a bemeneti tér particionálása alapján dekomponáltuk volna, ahol azonban a particionálás nem éles határokkal történik.

A lágy particionálás könnyen interpretálható egy olyan architektúra esetén, ahol csak két szakértőnk van. Az ezekhez tartozó két kapuzóérték g₁ésg₂. Írjuk fel g₁ kifejezését (nyilvánvalóan g₂= 1− g₁):

$g_{1} = \frac{e^{ξ_{1}}}{e^{ξ_{1}} + e^{ξ_{2}}} = \frac{1}{1 + e^{- {(v_{1} - v_{2})}^{T} x}}$ (9.31)

ami láthatóan egy olyan logisztikus gerincfüggvény (logistic ridge function), melynek orientációját a v₁-v₂ vektor iránya szabja meg. Mindazon x-ekre, melyek (v₁-v₂)-re merőlegesek a két kapuzóérték megegyezik: g₁=g₂= 1/2, vagyis ezekre a bemenetekre, melyeknél a logisztikus függvény gerince található, a MOE válasza a két szakértő válaszának átlaga. A gerinctől távolodva az egyik irányban az első szakértő, a másik irányban a második szakértő szerepe kezd nőni, mindig a másik szakértő rovására. A gerinc meredeksége v₂-v₁nagyságától függ. Ha v₂-v₁ nagy, a gerinc meredek, a két szakértő szerepe élesen elhatárolódik egymástól, míg kis értéknél az elválasztás lágy, a szakértők „kompetencia-területei” erősen átlapolódnak.

A MOE architektúra többszintű, hierarchikus hálóegyüttessé is kiterjeszthető, amikor a szakértőkből több csoportot alkotunk és ezeket a csoportokat külön-külön egy-egy MOE architektúrába fogjuk össze, majd a MOE kimenetekből egy újabb kapuzóhálózattal állítjuk elő a hierarchikus rendszer kimenetét. A hierarchikus MOE (HMOE) tehát nem a szakértőkből képez hierarchikus rendszert, hanem a kapuzóhálózatokból. A HMOE egy fa struktúrájú moduláris háló, melynek csak a leveleinél vannak szakértő modulok.

A MOE tanítása

A MOE architektúrának két, tanítással meghatározandó paraméter-készlete van. A $Θ_{i}$ paramétermátrixok a szakértők szabad paramétereiből állnak, míg a v_i vektorok a szoftmax függvényen keresztül határozzák meg a kapuzóhálózat leképezését. A tanítást most is egy $Z = {z_{l}^{}}_{l = 1}^{L} = {(x_{l}, d_{l})}_{l = 1}^{L}$ tanítópontkészlet alapján tudjuk elvégezni.

A háló tanítása többféle megközelítésben is lehetséges. Amennyiben az egyes szakértők neuronhálók, mind a $Θ_{i}$ szakértő-paraméterek, mind a v_i kapuzóhálózat-paraméterek a speciális MOE architektúrára alkalmazott hibavisszaterjesztéses algoritmussal taníthatók, hiszen a kimenet mind a $Θ_{i}$ , mind a v_i paraméterek folytonos függvénye. Ha a tanításnak ezt a megközelítését alkalmazzuk, akkor a MOE valójában nem több, mint egy speciális felépítésű komplex hálóarchitektúra. Ebben a megközelítésben a kapuzóértékekre megfogalmazott (9.29) feltételeknek nincs is különösebb jelentőségük, a feltételektől akár el is tekinthetünk. Ennél érdekesebb azonban, ha az architektúrához valószínűségi értelmezést rendelünk. A valószínűségi értelmezés a háló működését új megvilágításba helyezi, sőt a háló tanítása is más értelmezést nyer. A valószínűségi értelmezés mellett a háló tanítása maximum likelihood becslési problémaként fogalmazható meg. A következőkben ezt az interpretációt és az ennek megfelelő tanítási eljárást foglaljuk össze.

Tanítás valószínűségi értelmezés alapján

A valószínűségi értelmezésben mind a kapuzóhálózatok, mind a szakértők szerepe megváltozik. A kapuzóhálózat úgy is felfogható, mint egy olyan osztályozó, ami az x bemenővektort egy multinomiális valószínűségi változóra képezi le. A kapuzóértékekre megfogalmazott (9.29) feltételek biztosítják, hogy a g_i értékek valószínűségekként is értelmezhetők legyenek. g_i értelmezhető, mint az a valószínűség, hogy a kimenet az i-edik szakértőtől származik:

$g_{i} = P (i | x, v_{i})$ (9.32)

A kapuzóhálózat szerepe ekkor azt eldönteni, hogy melyik szakértő kimenete kerüljön ki a teljes moduláris rendszer kimenetére. A HMOE esetében több döntési szintet különböztethetünk meg, tehát egy hierarchikus döntési szekvencia eredménye az, hogy a kimenet melyik szakértőtől származik. Amennyiben ez a döntés vagy döntés-sorozat megszületett, feltételezhetjük, hogy a d kimenetet egy statisztikai modell generálta. Ez azt jelenti, hogy d valószínűségi változónak tekinthető, melyet valamilyen P valószínűség-sűrűségfüggvénnyel jellemezhetünk. Ennek megfelelően az egyes szakértőkhöz is valószínűségi értelmezés rendelhető és egy szakértő kimenete úgy interpretálható, mint a d valószínűségi változó feltételes várható értéke.

Ha a kimenet származtatását e szerint a valószínűségi értelmezés szerint nézzük, akkor először a szakértők válaszát kell tekintenünk. Egy szakértő a valószínűségi modell alapján az

$y_{i} = E (d | x, Θ_{i})$ (9.33)

feltételes várhatóértéknek megfelelően állít elő egy kimenetet, ahol a várhatóérték-képzést egy $P (d | x, Θ_{i})$ feltételes sűrűségfüggvény szerint képezzük. A következő lépésben egy szakértőkimenet a kapuzóértéknek megfelelő valószínűséggel kerül a teljes háló kimenetére (vagy HMOE esetében a következő hierarchiaszintre).

Ebből a valószínűségi modellből kiindulva annak valószínűsége, hogy adott x_l bemenetre d_l választ kapunk a teljes valószínűségek tétele alapján az alábbi formában írható fel:

$\begin{array}{l} P (d_{l} | x_{l}, Θ^{*}) = \sum_{i} g_{i} (x_{l}, v_{i}^{*}) P (d_{l} | x_{l}, Θ_{i}^{*}) \\ = \sum_{i} P (i | x_{l}, v_{i}^{*}) P (d_{l} | x_{l}, Θ_{i}^{*}) \end{array}$ (9.34)

A (9.34) összefüggésben a paraméterek melletti * azt jelzi, hogy itt a paraméterek „igazi”, de számunkra ismeretlen értékei szerepelnek. A $Θ^{*}$ az összes szakértő $Θ_{i}^{*}$ paramétereit összefogó eredő paramétermátrix. Amennyiben az igazi értékek helyett valamilyen $Θ_{i}$ és v_i paramétereink vannak, az l-edik tanítóponthoz tartozó bemenet és kimenet közötti valószínűségi kapcsolatot a

$P (d_{l} | x_{l}, Θ) = \sum_{i} P (i | x_{l}, v_{i}) P (d_{l} | x_{l}, Θ_{i})$ (9.35)

feltételes sűrűségfüggvény adja meg. A teljes tanítókészletre is felírhatjuk a valószínűségi kapcsolatot:

$P (d | x, Θ) = \prod_{l = 1}^{L} P (d_{l} | x_{l}, Θ) = \prod_{l = 1}^{L} [\sum_{i = 1}^{M} P (i | x_{l}, v_{i}) P (d_{l} | x_{l}, Θ_{i})]$ (9.36)

A (9.36) összefüggés annak valószínűségét adja meg, hogy az adott x_l bemenet mellett a megfelelő d_l kívánt választ kapjuk (l=1,2,…,L), feltéve, ha a szakértőink paramétermátrixai a $Θ_{i}$ mátrixok, a kapuzóhálózatunk paramétervektorai pedig a v_ivektorok (i=1,2,…,M).

A (9.36) összefüggés képezi a paraméterek meghatározásának, a MOE tanításának az alapját. Keressük ugyanis azokat a $Θ_{i}$ mátrixokat és v_ivektorokat, melyek mellett a (9.36) valószínűség-sűrűségfüggvény épp az adott tanítóponthalmaz esetén veszi fel a maximumát. A feladatot tehát visszavezettük egy maximum likelihood becslési problémára, ahol a likelihood függvényt épp (9.36) adja meg. A tanító összefüggések meghatározásának további lépéseiben a likelihood függvény helyett célszerű annak logaritmusával, a log-likelihood függvénnyel dolgozni.

$L (x, Θ) = log P (d | x, Θ) = \sum_{l = 1}^{L} log [\sum_{i = 1}^{M} P (i | x_{l}, v_{i}) P (d_{l} | x_{l}, Θ_{i})]$ (9.37)

A maximum likelihood becsléseredményét a (log-)likelihood függvény maximumát biztosító paramétervektorok szolgáltatják. A szélsőérték-keresést itt is gradiens módszerrel végezve meg kell határoznunk a

$\frac{\partial L (x, Θ)}{\partial Θ_{i}^{}} = 0$ és a $\frac{\partial L (x, Θ)}{\partial v_{i}} = 0$ (9.38)

likelihood egyenletek megoldásait. (Itt a $Θ_{i}$ mátrixokat formálisan vektorrá alakítva használjuk.) A gradiens-számításnál alkalmazva a láncszabályt a $Θ_{i}$ szerinti gradienst y_i-n keresztül, a v_i szerinti gradienst pedig ξ_i-n keresztül határozhatjuk meg:

$\frac{\partial L (x, Θ)}{\partial Θ_{i}^{}} = \frac{\partial L (x, Θ)}{\partial y_{i}} \frac{\partial y_{i}}{\partial Θ_{i}^{}}$ és $\frac{\partial L (x, Θ)}{\partial v_{i}} = \frac{\partial L (x, Θ)}{\partial ξ_{i}} \frac{\partial ξ_{i}}{\partial v_{i}}$ (9.39)

A részletektől eltekintve – feltételezve, hogy a valószínűségi interpretációban Gauss eloszlásunk van – a gradiens eljárás eredményeképp a következő tanító összefüggéseket nyerjük:

$Θ_{i} (k + 1) = Θ_{i} (k) + η \sum_{l = 1}^{L} h_{i, l}^{} (d_{l} - y_{i, l}) \frac{\partial y_{i, l}}{\partial Θ_{i}}$ (9.40)

és

$v_{i} (k + 1) = v_{i} (k) + η \sum_{l = 1}^{L} (h_{i, l}^{} - g_{i, l}^{}) x_{l}$ (9.41)

ahol η jelöli a tanulási tényezőt, y_i,l jelöli az i-edik szakértő x_l-re adott válaszát, g_i,laz i-edik kapuzóértéket az l-edik tanítómintánál, míg h_i,l-t az alábbi összefüggés definiálja:

$h_{i, l} = \frac{P (i | x_{l}, v_{i}) P (d_{l} | x_{l}, Θ_{i})}{\sum_{j} P (j | x_{l}, v_{j}) P (d_{l} | x_{l}, Θ_{j})}$ . (9.42)

A szakértőparaméter tanítására vonatkozó (9.40) összefüggés csak akkor alakítható tovább, ha ismerjük a szakértő felépítését. Lineáris szakértőt feltételezve, ahol a szakértő kimenetét

$y_{i, l} = Θ_{i}^{} x_{l}$ (9.43)

adja meg, a súlymódosító összefüggésre a következőt kapjuk:

$Θ_{i} (k + 1) = Θ_{i} (k) + η \sum_{l = 1}^{L} h_{i, l}^{} (d_{l} - y_{i, l}) x_{l}^{T}$ (9.44)

A (9.44) összefüggést szemügyre véve látható, hogy a szakértő paramétereinek módosítása a szakértő hibájától függ, hiszen az i-edik szakértő kimeneti hibáját az l-edik tanítópontban épp ( $d_{l} - y_{i, l}$ ) adja meg. Hasonló megállapítás tehető a kapuzóhálózat paraméterének tanító összefüggésére is, ugyanis a (9.41) összefüggés szerint a súlymódosítás h_i,l és g_i,l eltérésétől függ, ahol ez az eltérés is hibaként értelmezhető.

A MOE mindkét paraméterkészletének súlymódosító összefüggései függnek a (9.42) által definiált h_i,l értékektől. Vegyük észre, hogy amennyiben a $g_{i, l} = P (i | x_{l}, v_{i})$ valószínűségeket a priori valószínűségeknek tekintjük, a h_i,l értékek az a posteriori valószínűségek. Ez (9.42)-ből a Bayes szabály alkalmazásával közvetlenül adódik. A g_i,l kiinduló kapuzóérték ugyanis annak a valószínűségét adja meg, hogy adott x_l bemenet mellett az eredő kimenetet az i-edik szakértő válasza határozza meg. g_i,l értékét úgy határozzuk meg (vesszük fel), hogy az x_l-re adandó kívánt választ, d_l-t nem ismerjük. Ezzel szemben h_i,l azt az állapotot tükrözi, amikor már d_l-t is felhasználtuk, tehát h_i,l az l-edik tanító mintapár ismerete utáni állapotra vonatkozik. Ennek megfelelően

$h_{i, l} = P (i | x_{l}, d_{l}, v_{i})$ . (9.45)

Az (9.41) és az (9.44) összefüggések kötegelt (batch) tanításra vonatkoznak, vagyis amikor az összes tanítópont felhasználását követően történik a súlymódosítás. Ugyanakkor a MOE tanításánál is alkalmazhatunk mintánkénti súlymódosítást; ekkor a fenti összefüggésekben az l mintapont-index szerinti összegzés elmarad.

A MOE valószínűségi értelmezése lehetővé teszi, hogy a paraméterek meghatározást maximum likelihood paraméterbecslési eljárásra vezessük vissza. A maximum likelihood becslés az előbbiekben bemutatott gradiens alapú eljárásnál hatékonyabban is meghatározható. A MOE architektúrára származtatták az EM (expectation-maximization)^[7] alapú eljárást, mely a számítások egyszerűsítését eredményezi. Ennek részleteivel azonban itt nem foglalkozunk, csak a megfelelő irodalomra ([Jor94]) utalunk.

A MOE konstrukciója

A MOE, illetve a HMOE architektúrák konstrukciójánál is meg kell határozni a moduláris rendszer struktúráját. Ez itt a szakértők számának, illetve hierarchikus MOE esetében a hierarchia szintek számának a meghatározását is jelenti. A MOE/HMOE struktúrájának meghatározása a modellválasztás problémakörbe tartozik, így a modellválasztás eddig említett megközelítéseit alkalmazhatjuk. Leginkább az adatokból kiindulva, az eredmények folyamatos tesztelése útján, a kereszt kiértékelés alkalmazásával határozhatjuk meg a megfelelő MOE architektúrát.

HMOE konstrukciójánál gyakran alkalmaznak olyan eljárást, amely bináris fa struktúrájú hierarchikus moduláris rendszert eredményez. Erre ad lehetőséget például a CART (classification and regression tree) [Bre84] alapú eljárás, ahol a feladatot a kívánt válaszok alapján dekomponáljuk egyre kisebb részfeladatokra úgy, hogy az egyes lépésekben a problémateret mindig két részre hasítjuk. A dekomponálás alapja, hogy a problématér különválasztott tartományaihoz tartozó mintapontoknál a kívánt válaszok szórása minél kisebb legyen. A hierarchikus dekompozíció egy HMOE architektúrát eredményez, annak ellenére, hogy az egyes szakértők tulajdonképpen továbbra is a teljes feladatot oldják meg.

A MOE architektúráját nagymértékben befolyásolja, hogy az egyes szakértők milyen felépítésűek. Tipikus választás az egyszerű lineáris szakértő. Ebben az esetben az eredő feladat valójában szakaszonként lineáris működést valósít meg, ahol azonban az átmenet az egyes szakaszok között a szoftmax kapuzó függvények következtében folytonos és „legömbölyített”.

Bonyolult, komplex leképezésre képes szakértő modulok alkalmazása már csak azért sem célszerű, mert ekkor nagy a veszélye annak, hogy akár egyetlen szakértő is meg tudja oldani a feladatot. Ha ilyen eset áll elő, akkor ennek az egyetlen szakértőnek megfelelő kapuzóérték a teljes problématéren közel 1 értéket vesz fel, ami ennek a szakértőnek a hasznosítását és a többi indokolatlan alkalmazását jelenti. Az egyszerűbb képességű szakértők „garantálják”, hogy külön-külön egyikük sem képes a feladat megoldására, együttműködésükre feltétlenül szükség van. A MOE előnyei akkor érvényesülnek, ha a feladat valóban megoszlik az egyes szakértők között. Az előnyök között elsősorban a gyorsabb tanulást kell megemlíteni, de az egyszerű szakértők miatt általában az egész hálózat komplexitása is jóval kisebb lehet, mint egy hasonló képességű egyedi hálózaté.

Mesterséges Intelligencia Elektronikus Almanach

Elsődleges linkek