A Lagrange multiplikátoros módszer egy hatékony eljárás a feltételes szélsőérték-keresési feladatok megoldására.

Legyen adott egy $f\left(x\right)$ függvény $x\in {ℝ}^N$ és adottak a $g_i\left(x\right)=0$ feltételek. Keressük $f\left(x\right)$ szélsőértékét (minimumát vagy maximumát) úgy, hogy közben a $g_i\left(x\right)=0$ feltételek is teljesüljenek.

Definiáljuk az alábbi Lagrange függvényt:

$L\left(x,\alpha \right)=f\left(x\right)-{\displaystyle \sum _i^{}{\alpha }_i}{g}_i\left(x\right)$ (F.39)

ahol az ${\alpha }_i$ együtthatók a Lagrange multiplikátorok. Figyeljük meg, hogy mind a szélsőértékfeladat, mind a feltételek figyelembevétele szerepel a Lagrange függvény szélsőértékére vonatkozó feladatban. Ugyanis

${\nabla }_{x}L\left(x,\alpha \right)={\nabla }_{x}f\left(x\right)-{\nabla }_x{\displaystyle \sum _i^{}{\alpha }_i}{g}_i\left(x\right)$ (F.40)

vagyis

${\nabla }_{x}L\left(x,\alpha \right)=0\iff {\nabla }_{x}f\left(x\right)={\nabla }_x{\displaystyle \sum _i^{}{\alpha }_i}{g}_i\left(x\right)$ (F.41)

${\nabla }_{\alpha }L\left(x,\alpha \right)=0\iff g_i\left(x\right)=0$ (F.42)

A következő egyszerű kétdimenziós feladaton illusztráljuk a Lagrange multiplikátoros módszer működését. Legyen a kétdimenziós függvényünk $f\left(x\right)=2x_1^2+x_2^2$ . Keressük ennek a függvénynek a minimumát azzal a feltétellel, hogy $x_1^2+x_2^2=1$ , vagyis $g\left(x\right)=x_1^2+x_2^2-1=0$ . Az $f\left(x\right)$ függvény feltétel nélküli minimuma az $x={\left[\mathrm{0,0}\right]}^T$ pontban van. Ez a pont azonban nyilvánvalóan nem elégíti ki a $g\left(x\right)=0$ mellékfeltételt. A megfelelő Lagrange függvény:

$L\left(x,\alpha \right)=2x_1^2+x_2^2-\alpha \left(x_1^2+x_2^2-1\right)$ (F.43)

Melynek x szerinti gradiense

$\begin{array}{l}\frac{\partial L\left(x,\alpha \right)}{\partial x_1}=4x_1^{}-2\alpha x_1^{}=0\\ \frac{\partial L\left(x,\alpha \right)}{\partial x_2}=2x_2^{}-2\alpha x_2^{}=0\\ \frac{\partial L\left(x,\alpha \right)}{\partial \alpha }=-\left(x_1^2+x_2^2-1\right)=0\end{array}$ (F.44)

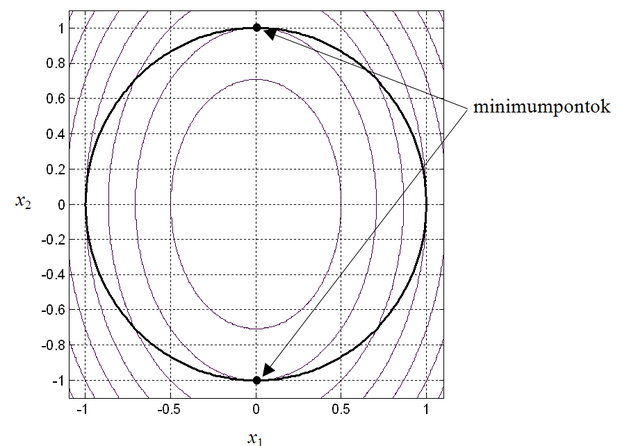
A két első egyenletből $\alpha =2$ illetve $\alpha =1$ adódik, mely értékek mellett $f\left(x\right)$ minimumát az $x_1^{}=0;x_2^{}=\pm 1$ pontban kapjuk (F.3.1 ábra).

F.3.1. ábra - Mintapélda a feltételes szélsőérték-keresésre. A vékonyabb vonallal rajzolt ellipszisek a minimalizálandó f(x) függvény szintvonalai, a vastagabb vonallal rajzolt kör pontjai a mellékfeltételnek megfelelő pontok. A két fekete pont a feltételes minimumot biztosító pontok.

Az ábrán jól látható, hogy az $f\left(x\right)$ függvény által meghatározott szintvonalak gradiensvektorai a feltételes minimumpontokban azonos irányúak, mint a mellékfeltételt megadó kör gradiensvektorai, vagyis a minimumpontokban a két görbe érinti egymást.