3.2. Példaproblémák
A 8-királynő probléma (8-queens problem) az egyik legöregebb algoritmuselméleti probléma, sakkfeladvány. A probléma lényege, hogy 8 királynőt (melyeket szokás vezérnek is nevezni) kell elhelyezni egy hagyományos 8 x 8-as sakktáblán, oly módon, hogy azok a sakk szabályai szerint ne kerüljenek ütésbe. Ehhez a királynő (vezér) lépési lehetőségeinek ismeretében az szükséges, hogy egynél több bábu ne legyen azonos sorban, azonos oszlopban, illetve átlóban.
A 8-királynő probléma tulajdonképpen egy speciális esete az ennél általánosabb n-királynő problémának. Ezen probléma azt a kérdést veti fel, hogy hányféleképpen lehet lerakni „n” darab királynőt (vezért) egy n x n-es sakktáblán.
A problémát először Max Bezzel (1824. február 4. - 1871. július 30.), német sakkozó vetette fel 1848-ban [1]. A probléma azért is bizonyult izgalmasnak, mert látszólag néhány próbálkozás árán megfejthető, az egzakt megoldás azonban csak a matematika komolyabb eszközeinek használatával található meg. Az évek során sok matematikus – többek között Carl Friedrich Gauss (1777. április 30. - 1855. február 23.), német matematikus és természettudós [2], illetve Georg Cantor (teljes nevén: Georg Ferdinand Ludwig Philipp Cantor), (1845. március 3. - 1918. január 6.), orosz születésű és élete jelentős részét Németországban töltő matematikus – foglalkozott vele és az általánosított n-királynő problémával [3]. Gauss elsőre csak 72 megoldást talált meg a lehetséges összes 92-ből (a 8-királynő problémára).
Az első megoldást Franz Nauck, német matematikus adta 1850-ben, aki szintén foglalkozott a feladat n x n-es kiterjesztésével, az n-királynő problémával, mely probléma felvetését sokan neki tulajdonítják [4].
24 évvel később, 1874-ben S. Günther egy látszólag egész más terület, a determinánsok segítségével jutott eredményre, amivel lerakhatók a bábuk. Később ezt az eljárást finomította James Glaisher (teljes nevén: James Whitbread Lee Glaisher), (1848. november 5. - 1928. december 7.), angol matematikus [5] [6].
Edsger Dijkstra (teljes nevén: Edsger Wybe Dijkstra), (Rotterdam, 1930. május 11. - Hollandia, Nuenen, 2002. augusztus 6.), holland matematikus, informatikus, 1972-ben arra használta ezt a problémát, hogy bemutassa a strukturált programozás előnyeit, erejét. Publikált egy részletes leírást a probléma egy lehetséges megoldását jelentő backtrack algoritmusról („depth-first backtracking algorithm”) [7] [8]. A későbbiekben ez az algoritmus részletesebben is kifejtésre kerül.
A megoldás nehezen számítható, mivel a bábuknak összesen (64 „alatta” 8) = 4426165368 különböző lerakása létezik, de ebből csak 92 felel meg a 8-királynő probléma szabályainak. Ez igen nagy számítási időt jelent kimerítő keresést alkalmazva. Az összes lehetséges lerakások száma, és ezáltal a számításhoz szükséges idő csökkenthető azáltal, hogy bevezetünk egy olyan egyszerű és magától értetődő szabályt, miszerint minden sorban (vagy oszlopban) csak egy-egy bábu állhat. Így a vizsgálandó lerakások száma 8^8 = 16777216-ra redukálódik. Ez 16884-szer kevesebb, mint az első esetben, kimerítő keresést feltételezve. Ugyan még ebben az esetben is kimerítő keresést alkalmazunk, bizonyos lehetőségeket kihagyva, de n = 8 királynő esetén, egy 8 x 8-as sakktáblán már kezelhető lépésszámhoz jutunk. Ugyanakkor nagy „n” esetén, például n = 1.000.000-ra továbbra is megengedhetetlenül nagy a lépésszám. Mint azt láthatjuk, a „próbálgatáson” alapuló kimerítő keresésnél intelligensebb keresési algoritmusra van szükségünk a probléma polinomiális időben történő megoldásához.
Első megközelítésben alkalmazzunk egy egyszerű intuitív megoldást. A sakktábla legbaloldalibb oszlopába helyezzünk el egy királynőt (legfelső = legkisebb sorszámú sorba, a sorok sorszáma lefelé haladva növekszik). Ezt követően minden – még nem foglalt – legbaloldalibb (üres) oszlopba helyezzünk egy-egy királynőt, úgy hogy azt ne támadja egyetlen másik sem. Tehát az adott királynőt mindig a legkisebb sorszámú olyan sorba helyezzük, ahol az nem kerül ütésbe. Ha a királynő egy adott sorban ütésbe kerülne, akkor az adott királynő oszlopában ahhoz a sorhoz tartsuk nyilván, hogy hány darab másik királynő által kerülne ütésbe. Ha a lerakás során olyan eset fordulna elő, hogy az adott királynőt bármelyik sorba is helyeznénk, az mindig ütésbe kerülne más királynő/királynők által, akkor a királynőt helyezzük abba a legkisebb sorszámú sorba, ahol az a legkevesebb másik királynővel kerülne ütésbe. Ezzel a lépéssel azonban nem lenne helyes a lerakás, ezért a most lerakott királynőtől balra eső oszlopban (konkrétan abban az oszlopban, ahonnan a királynőnk „ütve van”), (nyilván ez az oszlop létezik, hiszen a tőlünk balra eső „térfélről” kerültünk ütésbe) helyezzük a királynőt az abban az oszlopban lévő legkisebb sorszámú olyan sorba, ahol az a legkevesebb, tőle balra eső királynővel kerülne ütésbe. Szerencsés esetben létezik olyan sor is, ahol a királynő nem kerül ütésbe. Nyilván ekkor az előbbi szabálynak megfelelően ezt a sort választjuk, illetve ha több ilyen sor is van, akkor ezek közül a legkisebb sorszámút. Ebben az esetben már helyes a lerakás, ellenkező esetben ismételjük az eljárást addig (mindig balra haladva), amíg végül helyes lerakáshoz jutunk (mindig lesz ilyen). Majd, ha még maradt bábunk, akkor azokat is hasonlóan próbáljuk meg lerakni. Ez az eljárás biztosan ad jó megoldást. Az eljárással csak kb. 2000 állapot fordul elő.
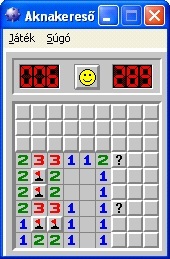
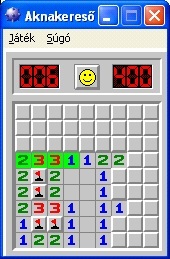
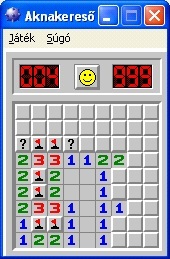
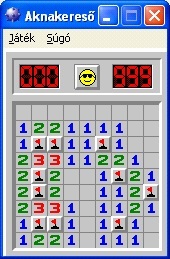
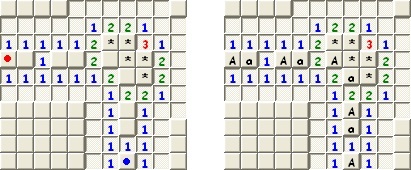
A következő ábrákon az előbb ismertetett megoldás egy-egy lépése látható. Az első ábrán látható egy olyan esetre példa, amikor az utolsó bábu lerakásakor minden sorban ütésbe kerülünk valamelyik másik bábuval/bábukkal. A második ábrán látható példa az ütésben lévő bábu megfelelő sorban történő elhelyezésére. A harmadik ábrán az előbbi lépéssel kialakuló helytelen lerakás javítása látható a megfelelő bábumozgatással. A negyedik ábrán pedig az eljárás egy lehetséges és egyben helyes megoldása látható.
Az előbb ismertetett eljáráshoz nagyon hasonló a következőkben ismertetendő backtrack (visszalépéses) algoritmus.
A backtrack algoritmus sokban hasonlít a korábban ismertetett intuitív algoritmusunkra, talán még egyszerűbb is annál [9] [10]. Itt ugyanis nem számoljuk az egyes mezőkben, hogy a királynőt az adott mezőre léptetve hány másik királynővel kerülne ütésbe, egyszerűen csak az első alkalmas pozícióba helyezzük azt. Ütés esetén is csak a szomszédos királynő pozícióját befolyásoljuk közvetlenül. Az algoritmus futásának kezdetén természetesen egyetlen királynő sem tartózkodik a sakktáblán. A lerakás során a királynők elhelyezésével oszloponként balról jobbra haladunk. Minden egyes királynő elhelyezése során soronként vizsgáljuk, hogy az alkalmas-e a királynő lerakására. Ha nem, úgy haladunk a következő sorra, egészen addig, míg meg nem találjuk az első alkalmas sort (ahol a királynőt el is helyezzük). Előfordulhat, hogy ilyet nem találunk, ebben az esetben visszalépünk az előző oszlopra, majd eltávolítjuk az ott tartózkodó királynőt. A korábbi pozíciójából eltávolított királynőnek ugyanebben az oszlopban, a korábbi pozícióját követő sorokban keresünk helyet. Ha ilyet találtunk, úgy a visszalépegetés befejeződik, és ismét megpróbáljuk az eredeti királynőnket elhelyezni. Ha a korábbi királynőnknek nem találtunk alkalmas (új) pozíciót, úgy ismét visszalépünk, és ez ismétlődik mindaddig, míg valamelyik oszlopban az adott királynőt nem sikerül végre új pozícióban elhelyezni. Természetesen, ha a sorok végére értünk és ezáltal adott lépésben nem adódott megoldás az elhelyezésre, akkor az újbóli elhelyezés alkalmával a sor elejétől kezdjük újra a próbálgatást.
Az algoritmus működését a következő példán szemléltethetjük.
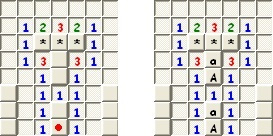
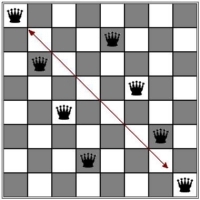
Az első öt királynő elhelyezése nem okoz gondot, a hatodik királynő azonban bármelyik sorba helyezve ütésbe kerül. Ezt az állapotot láthatjuk az alábbi ábrán:
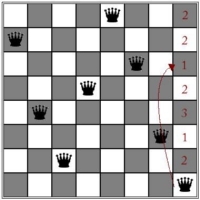
Ebben az esetben vissza kell lépnünk (24. lépésben) és az előző oszlopban tartózkodó királynőnek új helyet kell keresnünk. Szerencsére találunk számára alkalmas helyet. Az áthelyezést szemlélteti a következő ábra:
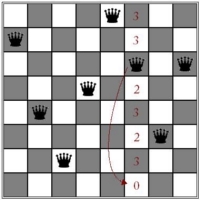
Mivel királynőnknek találtunk alkalmas új pozíciót, ezért további visszalépésre nincs szükség. Próbáljuk meg újra elhelyezni a hatodik oszlopba kerülő királynőt. Mint az a fenti ábrán is látható, ez továbbra sem fog sikerülni. Ekkor tehát újra vissza kell lépnünk (36. lépésben). Mivel azonban az eggyel korábbi királynőnknek sem találunk már új pozíciót (hiszen az utolsó sorban volt), ezért ismét vissza kell lépnünk és megpróbálni elhelyezni új pozícióba a negyedik oszlopban lévő királynőt. Ez, illetve a rákövetkező lépések láthatók az alábbi ábrán:
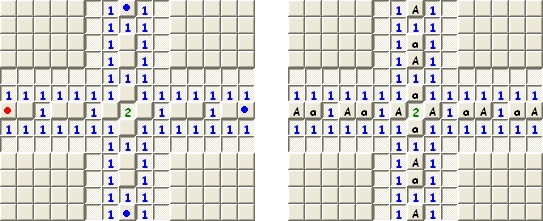
A 60. lépés sajnos ismét kudarcba fullad. Ez jól látható a fenti ábrán.
Egy lehetséges jó megoldást a 876. lépésben kapunk, amely a következőképpen néz ki:
Az algoritmust a következőképpen implementálhatjuk (a C++ nyelvhez közeli szintaxissal):
Legyen egy „proba” nevű metódusunk, amely tulajdonképpen az algoritmus lényegi részét valósítja meg. A metódus egyetlen paramétere az adott sakktábla oszlop azonosítója. Vegyünk fel két változót „siker”, illetve „sor” néven. A „siker” gyakorlatilag egy logikai (bool) típusú változó, mely igaz és hamis értékeket vehet fel. Benne mindig azt tároljuk, hogy az adott lépésben sikerült-e elhelyeznünk az épp aktuális királynőt. Kezdetben az értékét logikai hamis értékre állítjuk. A „sor” változó (például integer típusú változó) pedig azt tárolja, hogy a próbálgatás során éppen melyik sorban vagyunk. A kezdő sorszámot 1-re állítjuk, hogy a legfelső sortól kezdjük a próbálgatást. Az inicializáló szakaszt követően kezdjük meg a királynő elhelyezésének próbálgatását rekurzív módon, soronként lefelé haladva. Ha az adott lépésben a mező nem volt szabad (vagyis azon ütésbe kerültünk volna), akkor egyszerűen csak növeljük a sorszámot (vagyis a következő sorra lépünk). Nyilván ekkor a próba sikertelen marad. Ha a mező szabad volt, akkor lefoglaljuk, majd ha még van vissza oszlop (és így elhelyezendő királynő), akkor megpróbálkozunk a következő oszlopban királynőt elhelyezni (és ez rekurzív módon folytatódik). Ha az utolsó oszlopon is túlhaladtunk, akkor a „siker” értéke igaz érték lesz. Egy adott oszlopban mindig a következő oszlop sikerességét vizsgáljuk, és ha az nem volt sikeres, úgy az aktuális oszlopból töröljük a királynőt (felszabadítjuk), hiszen annak is új pozíciót kell keresnünk. Mindezt addig folytatjuk, míg az a feltétel fennáll, hogy nem jártunk sikerrel és nem is jártuk be még az összes sort. Ha a feltétel valamelyik fele sérül (vagy mindkettő), úgy a „siker” változó aktuális értékével térünk vissza.
Vagyis a „proba” nevű metódusunk a következőképpen épül fel:
bool proba(int oszlop) {
bool siker = false; sor = 1;
do {
if(szabad(sor, oszlop)) {
lefoglal(sor, oszlop);
if(oszlop < 8) siker = proba(oszlop + 1);
else siker = true;
if(!siker) felszabadit(sor, oszlop);
}
sor++;
} while(!siker && sor <= 8);
return(siker);
}
A „szabad” metódus a következő alakú:
bool szabad(int sor, int oszlop), amely megvizsgálja, hogy az adott helyre lehet-e királynőt tenni vagy sem (gyakorlatilag megnézi, hogy a királynő ütésben lenne-e).
A „lefoglal” metódus egyszerűen elhelyezi a királynőt az adott mezőn (például egy 8 x 8-as kétdimenziós tömb megfelelő elemét 1 értékre állítja), míg a „felszabadit” metódus a királynőt eltávolítja onnan (például nullázza a tömb adott elemét).
Az algoritmus elindításához csak meg kell hívnunk a „proba” metódust azzal az oszlopindexszel, amely oszloptól kezdve akarjuk a királynőket letenni. A metódus visszatérési értéke a lerakás sikeressége lesz (igaz = sikerült, hamis = nem sikerült). Ha a lerakás sikeres volt, akkor a módosított adatszerkezetből (például az előbbi tömbből) kiolvasható a bábuk helyzete.
Kiindulásképpen tegyük fel, hogy már van egy megoldásunk (n-1) x (n-1)-es táblára, amely megoldás alatt itt azt értjük, hogy vele megkapjuk valamennyi lehetséges elhelyezést az (n-1) x (n-1)-es táblán. Helyezzük az n-edik királynőnket az n-edik sor és n-edik oszlop találkozásánál lévő pozícióba. Máshova nem is tehetnénk, hiszen az első (n-1) sor, illetve oszlop biztosan foglalt. Hamar rájöhetünk azonban, hogy ez a megoldás sajnos nem adja meg az összes lehetséges lerakást, hiszen olyan helyes megoldások is léteznek, ahol egyik sarokban sincs királynő. (Például n = 4 esetén jó megoldás az is, amikor az első sor második, a második sor negyedik, a harmadik sor első, illetve a negyedik sor harmadik oszlopában helyezkednek el a királynők.) Ráadásul a királynőknek nem feltétlenül kell úgy elhelyezkedniük, hogy azok valamennyien az n x n-es tábla első (n-1) x (n-1)-es táblarészén helyezkednek el. Tehát más megoldást kell találnunk. Azt feltételezhetjük, hogy adott egy megoldásunk, amely (m-1) királynőt helyez el az n x n-es tábla (m-1) x n-es táblarészén. Itt az „m” 2-től n-ig bármi lehet. Természetesen a végső, n x n-es megoldásban az első (m-1) sorban elhelyezkedő királynőre is igaznak kell lennie, hogy azok nem ütik egymást, hiszen ha ütnék, akkor nem lenne jó megoldás ez a végső megoldás. Ezek a királynők pontosan (m-1) oszlopot használnak fel az n-ből (ezeknek tehát nem kell feltétlenül szomszédosaknak lenniük). Most már csak arra van szükségünk, hogy hogyan lehet az m-edik királynőt elhelyezni az m-edik sorban úgy, hogy helyes elhelyezéshez jussunk az (m x n)-es táblán. Ennek a megoldása nyilván az lesz, hogy az aktuális királynőt az adott sor összes mezőjébe megpróbáljuk elhelyezni, és csak azokat a lehetőségeket jegyezzük fel, ahol a királynő nem került támadásba. Az (1 x n)-es táblán még nyilván „n” megoldás adódik. Az előbbi gondolatmenetet követve könnyen beláthatjuk, hogy az m-edik sorig eljutva az (m x n)-es tábla összes megoldását megkapjuk. Az is jól látható, hogy a sorokon haladva („m” növekedésével) a megoldások fa-szerűen szétágaznak. A végső (n x n)-es megoldást akkor kapjuk, ha „m” értékével elérjük „n” értékét. Ehhez pontosan (n-1) iterációra van szükségünk. [11]
Egy JAVA programnyelven megvalósított, forráskóddal adott, animált rekurzív megoldás található a következő címen:
The Eight Queens – Animation of Recursion
A 8-királynő problémára és általánosságban az n-királynő probléma megoldására található demo a következő címen:
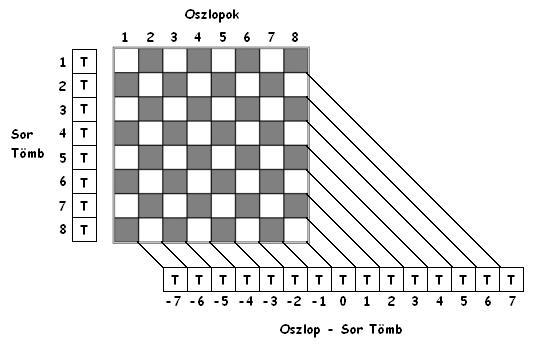
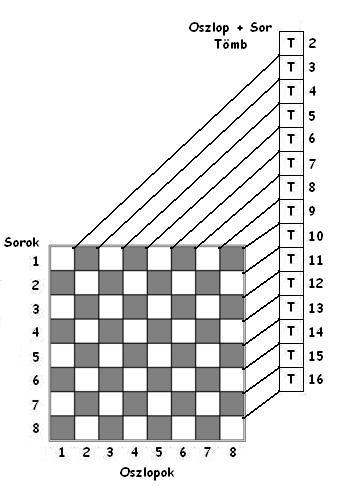
Az algoritmus egy „trükkös” adatszerkezetet használ, amely 3 logikai (bool) típusú egy dimenziós tömbből áll. Ezek a tömbök tartják nyilván a sakktábla mezők státuszát a királynők szempontjából. A logika „igaz” tömbelem azt jelenti, hogy az adott sorban vagy átlóban nem található királynő. A logikai „hamis” érték pedig azt jelenti, hogy az adott sorban vagy átlóban már van vezér. Az algoritmus futásának kezdetén minden tömbelem „igaz” logikai értékre van inicializálva. A „sor” tömb elemei a sakktábla egy-egy sorának felelnek meg, a tömbelemek 1-től 8-ig számozódnak. Ha egy királynőt helyezünk az n-edik sorba, akkor ennek a tömbnek az n-edik eleme „hamis”-ra változik. A másik tömb az „oszlop-sor” tömb. Ennek az elemei -7-től 7-ig számozódnak és megfelelnek az egyes oszlop és sor indexek különbségének. Végül a harmadik tömb az „oszlop+sor” tömb. Ennek az elemei 2-től 16-ig számozódnak és megfelelnek az egyes oszlop és sor indexek összegének. Az egyes tömbök tartalmának jelentése a következő ábrán is megfigyelhető:
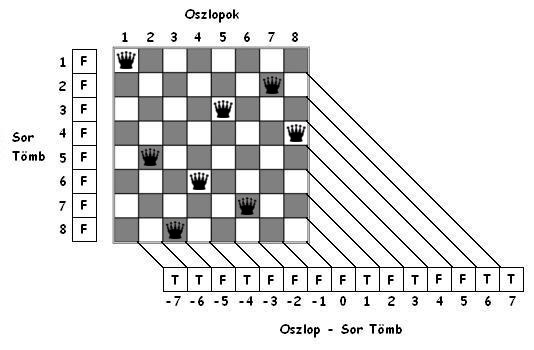
Példaként tekintsük a következőt: Helyezzünk el egy királynőt a sakktábla második oszlopának harmadik sorába. Ekkor a „sor” tömb 3-adik eleme, az „oszlop-sor” tömb -1-edik eleme és az „oszlop+sor” tömb 5-ödik eleme „hamis” értékű lesz. Az algoritmus a korábban megismert backtrack algoritmushoz hasonlóan működik, azzal a különbséggel, hogy itt most akkor állítunk be királynőt az adott sor és oszlop találkozásánál lévő mezőre, ha a mezőhöz tartozó mindhárom tömbelem logikai „igaz” értékű [12].
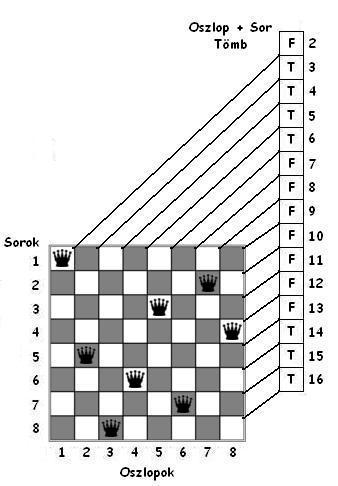
Az algoritmus első megoldását a következő ábra szemlélteti:
Ahogy korábban már említettük, az n-királynő probléma azt a kérdést veti fel, hogy hányféleképpen lehet n darab vezért elhelyezni egy n x n-es sakktáblán. A probléma összes megoldását megkaphatjuk a fentebb ismertetett rekurzív eljárással.
A következő táblázatban az n-királynő probléma különböző, illetve lényegesen különböző megoldásainak száma látható (N <= 21) értékekre. Lényegesen különböző megoldások alatt azt értjük, amelyek nem vihetők át egymásba forgatással és tükrözéssel. A táblázat utolsó oszlopában az is látható, hogy az összes megoldás megtalálása mennyi időt venne igénybe backtrack algoritmussal, egy mai modern processzoron (Athlon XP 2100+ (1.73 GHz)) végezve a számolást.
Az alábbi táblázatban pedig az látható, hogy mennyi lenne egy backtrack algoritmus lépésszáma (egy lehetséges megoldásra) az egyes esetekben.
Az N-királynő probléma analitikus megoldásán azt értjük, hogy egy y = a * x + b alakú lineáris függvény formájában keressük a lehetséges lerakásokat, ahol a lerakás egy n x n-es táblára (n x n-es véges síkra) történik, „x” és „y” jelentik egy adott királynő (x, y) alakú koordinátáit, "a" nem egyenlő 1-gyel vagy -1-gyel és a koordináták 0-tól indulnak, n pedig egy prímszám, amely egyben az elhelyezendő királynők számát is jelöli.
Például: n = 7 és y = 2 * x vagy n = 7 és y = 3 * x + 1.
n = 7 esetén az analitikus megoldásokat azok az y = a * x + b alakú függvények adják, ahol „a” = 2, 3, 4, 5 és „b” = 0, 1, 2, 3, 4, 5, 6. Ebből látható, hogy összesen 4 x 7 = 28 analitikus megoldást találhatunk. [15]
A probléma analitikus megoldásainak és az összes megoldás számának aránya néhány kis „n” érték esetén [15]:
N = 5: 10/10: 100%
N = 7: 28/40: 70%
N = 11: 99/2680: 4%
Hasonló probléma még az úgynevezett n-szuperkirálynő probléma. Ennél a problémánál úgynevezett „szuperkirálynőket” kell a táblára helyezni (belőlük is n-et). A szuperkirálynő annyiban különbözik a klasszikus sakkbeli királynőtől, hogy lóugrásban is képes ütést végrehajtani.
A problémának összesen 92 megoldása létezik. Ezek közül összesen 12-t tekinthetünk egyedinek, a többi megoldás ugyanis ebből a 12-ből forgatással és/vagy tükrözéssel előállítható. A probléma összes egyedi megoldása a következő ábrán látható [16].
A 8-királynő probléma inkább az érdekes logikai feladványok, a szórakoztató matematika témakörébe tartozik. Mindemellett a probléma alkalmas a backtrack algoritmus bemutatására, illetve ezen keresztül a strukturált programozás erejének szemléltetésére. Egzakt módon igazából nem alkalmazzák technológiai eljárások részeként, viszont bizonyos rekurzív (akár backtrack), illetve egyéb keresési algoritmusok összehasonlítására kiválóan alkalmazható. A programozással ismerkedők számára alkalmas gondolkodtató gyakorlópélda, amelyen keresztül gyakorolható a különböző, programozásban használt adatszerkezetek használata, implementálása (például a kétdimenziós tömböké), a rekurzív gondolkodás, probléma-megközelítés. Akár kombinatorikai feladványok alapjául is szolgálhat.
Általánosításának, az n-királynő problémának egy lehetséges alkalmazási területe az „iparban” a számos videó képkódoló (tömörítő) szabványban (például az MPEG-1/2/4-ben is) alkalmazott, úgynevezett blokk mozgásbecslés (Block Motion Estimation) algoritmusának gyorsítása, az algoritmus során a blokkon végzett műveletek számának redukálása.
[1] ”Max Friedrich Wilhelm Bezzel” by Hans Siegfried
[2] ”Information on the n Queens problem” by Frank Ruskey and Susan Ruskey
[3] ”Georg Ferdinand Ludwig Philipp Cantor” by J. J. O'Connor and E. F. Robertson
[4] ”Algorithms: Backtracking” by Jeff Erickson
[5] ”Eight queens puzzle” by Chesspedia
[6] ”James Whitbread Lee Glaisher” by J. J. O'Connor and E. F. Robertson
[8] ”Edsger Wybe Dijkstra” by J. J. O'Connor and E. F. Robertson
[9] ”Backtracking” by David Matuszek (a Backtrack algoritmus általánosságban)
[10] ”Nyolc királynő probléma” by Szeberényi Imre
[11] ”Programming Problem: Solve the Eight-Queen Problem with Recursion” by yuonlamp.com
[12] ”Solving The Eight Queens Problem (WIRTH's Algorithm)” by F.C. Kuechmann
[13] ”N Queens Problem (number of Solutions)” by ic-net
[14] ”The N by N Queens Problem” by Peter Alfeld
[15] ”Solutions to the 8-Queens Problem” by Prof. Tadao Takaoka
[16] ”Queens Problem” by the MathWorld Team
Szerző: Kamarás Roland, BME
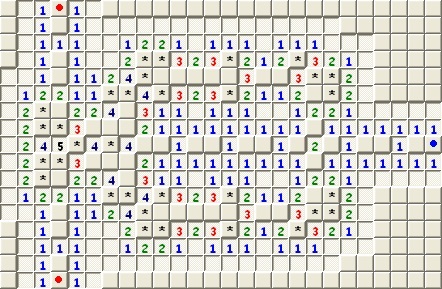
Az aknakereső egy népszerű egyszemélyes logikai játék, amely szinte minden mai személyi számítógépen megtalálható. A játék első változatai a 80-as évek elején jelentek meg, ma ismert formájában 1990-ben, a Microsoft cég Windows Entertainment Pack nevű játékgyűjteményének részeként látott napvilágot. A játék (a pasziánsszal egyetemben) a Windows 3.1 kiadása óta része az operációs rendszernek, így felhasználók milliói játsszák rendszeresen. A legtöbb számítógépes játékkal ellentétben az aknakereső során a játékosnak sokkal inkább az eszére, semmint ügyességére kell hagyatkoznia. A játék elé egyszerű ahhoz, hogy könnyedén meg lehessen érteni a szabályokat, ugyanakkor elég komplex ahhoz, hogy ne váljon gyorsan unalmassá. A későbbiekben látni fogjuk, hogy a játék még egy számítógép számára is kellően bonyolult, jelenleg nem ismert hatékony algoritmus, amely képes lenne hibátlanul megoldani minden aknakereső-táblát.
A játékot (alapvetően) egy személy játssza egy téglalap alakú, cellákra osztott pályán. A játék elején a számítógép előre megadott számú aknát helyez el véletlenszerűen kiválasztott cellákban, a játékos elől elrejtve. A játékos ezután bármelyik cellára rákattinthat. Ha a kiválasztott cellán akna van, a játékos vesztett, ellenkező esetben a gép ráírja a cellára, hogy a vele közvetlenül szomszédos 8 cella közül pontosan hányon van akna. A játékos a kapott információk alapján ismét kattint, és ez így megy addig, amíg egyszer vagy aknára nem kattint, vagy fel nem fedi az összes aknamentes mezőt.
A játéknak van egy kétszemélyes változata is, amely leginkább az MSN Messenger szoftverbe épített kliens által ismert. Ebben a változatban ellentétes a cél: a játékosoknak az aknamentes mezők helyett az aknákra kell kattintaniuk. Ha valaki eltalál egyet, újra ő jön; ha nem aknára kattint, a másik játékos használhatja fel a kattintás során szerzett új információkat az aknák keresésére. A két játékmód között alapvető különbségek vannak – míg egyjátékos módban csak arra kell ügyelnünk, hogy nem biztos kattintás esetén minél nagyobb valószínűséggel kattintsunk aknamentes mezőre, két játékos esetén azt is figyelembe kell vennünk, hogy minél kevesebb információt szolgáltassunk a másik játékosnak.
Ha matematikai szempontból vizsgáljuk a játékot, az alábbi kérdések merülhetnek fel egy adott játékállapottal kapcsolatban:
-
Konzisztens-e ez az állapot, azaz van-e olyan aknaelrendezés, ami nem mond ellent a már ismert adatoknak?
-
Mely mezők azok, amelyeken biztosan van akna?
-
Mely mezők azok, amelyeken biztosan nincs akna?
-
Az előző két kategória egyikébe sem tartozó mezők mekkora valószínűséggel tartalmaznak aknát, ha minden lehetséges aknaelrendezést azonos valószínűségűnek tekintünk?
A későbbi tárgyalás egyszerűsítése érdekében vezessük be az alábbi kifejezéseket:
-
biztonságos mező: olyan mező, amiről biztosan tudjuk, hogy nincs rajta akna
-
megjelölt mező: olyan mező, amelyről biztosan tudjuk, hogy van rajta akna
-
mező aknaszáma: egy mező aknaszáma azt fejezik ki, hogy hány vele szomszédos mezőn van akna
-
felfedett mező: olyan (biztonságos) mező, amelynek ismerjük az aknaszámát
-
üres mező: nem biztonságos és nem megjelölt mező
-
telített mező: olyan mező, aminek aknaszámával megegyező számú megjelölt szomszédja van
A későbbiekben látni fogjuk, hogy a játék által felvetett problémák még egy számítógép számára is meglehetősen bonyolultak. Van azonban pár stratégia, amelyek alkalmazásával emberi játékosok is meg tudnak oldani különböző állásokat.
Az egyik legegyszerűbb ilyen a „fennmaradó helyek” stratégiája: ha egy mezőnek pontosan annyi üres szomszédja van, mint amekkora az aknaszámának és a vele szomszédos megjelölt mezők számának különbsége, akkor az összes fel nem fedett szomszédján akna van, így azok megjelölt mezőkké válnak. Hasonlóan egyszerű stratégia az, hogy egy telített mező összes üres szomszédja biztonságossá tehető (és felfedhető), mert a telített mezőnek már az összes szomszédos aknáját felderítettük. A harmadik, legegyszerűbb stratégia az, hogy egy 0 aknaszámú mező minden szomszédja biztonságos, így felfedhetjük őket. (Ezt a stratégiát a játék tipikus implementációi automatikusan megvalósítják, ezért lehetséges az, hogy egyetlen kattintással több mezőt is felfedjünk egyszerre.)
Az előbb vázolt két (illetve három) stratégia igen hasznos, hiszen egy csomó következtetést levonhatunk gondolkodás nélkül. Ráadásul a második stratégia segítségével nagy mennyiségű új mezőt felfedhetünk, amelyekre újra alkalmazható az első stratégia... Ám nagyon hamar belefutunk egy olyan helyzetbe, amikor már nem segítenek ezek a módszerek. Ilyenkor jönnek jól a különböző ismert minták.
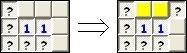
Az első minta, amivel megismerkedünk, az 1-1 minta:
Az első ábra bal oldalán kérdőjellel jelölt mezők aknaszáma lényegtelen, a lényeg csak az, hogy biztonságos mezők. (Az is előfordulhat, hogy a tábla szélén találjuk meg a mintát, így a ?-es mezők hiányoznak.) Ha valahol meglátjuk a fenti mintát, levonhatjuk a következtetést, hogy a bal oldali 1-es miatt a sárga hátterű mezők közül pontosan egyen van akna. Bármelyik mezőn is van az akna, az telítetté teszi a jobb oldali 1-est, így a minta alapján levonható a következtetés, hogy az ábra jobb oldalán (újonnan) kérdőjellel jelölt mező biztonságos. (Sőt, a jobb oldali 1-es összes eddig üres szomszédja is biztonságosnak minősíthető. Azért épp a kérdőjellel jelöltet emeltem ki, mert a mintát legtöbbször felfedett mezők összefüggő tartományainak egyenes határán szoktuk alkalmazni.)
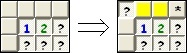
A másik alapminta az 1-2 minta:
A gondolatmenet hasonló: a két sárgával jelölt mező közül legfeljebb az egyiken van akna (az 1-es miatt). Levonható következtetésként, hogy a csillaggal jelölt mezőn biztosan akna van, így azt meg kell jelölnünk. Mivel a 2-es aknaszámú mező szomszédságában kell lennie még egy aknának, kimondhatjuk, hogy a sárga mezőkön pontosan egy akna van. Ettől viszont az 1-es mező telítetté válik, így (többek között) a jobb oldali ábrán kérdőjellel jelölt mezőről megállapíthatjuk, hogy biztonságos.
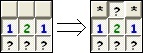
Az 1-2 minta kétszeri alkalmazásával keletkezik az egyik leghíresebb minta, az 1-2-1 minta (a két mintaillesztés után még egy telítésellenőrzést is végzünk a 2-es mezőre):
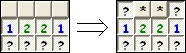
A másik híres minta az 1-2-2-1 minta (itt is észrevesszük, hogy a 2-es mezők telítettek):
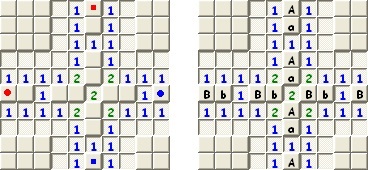
Ezzel a néhány mintával (főleg az utolsó kettővel) már meglehetősen jó eredményeket lehet elérni. Álljon itt egy példa! Néhány kattintás után az 5. ábrán látható állapotba jutottam egy aknakereső-játszma során.
A 5. ábrán sárgával jelölt mezőkön felismertem egy 1-1 mintát, amiből következően a 6. ábrán kérdőjellel jelölt mezőről megállapítottam, hogy biztonságos. Ekkor újabb 1-1 mintát találtam, amiből a 7. ábrán látható következtetést vonhattam le. Első pillantásra itt nem találtam semmit, ezért felfedtem a korábban biztonságosnak minősített mezőket. Ez látható a 8. ábrán. Ekkor vettem észre egy „rejtett” 1-2-2-1 mintát (a 8. ábrán zölddel jelölve): ha a zölddel jelölt mezők aknaszámából levonjuk a már megtalált aknaszomszédok számát, épp egy 1-2-2-1 mintát kapunk, így az 9. ábrán látható következtetéseket vontam le. Ezután felnyitottam a kérdőjeles mezőket, és kizárólag a két alapstratégia (fennmaradó helyek és telítettség vizsgálata) segítségével megoldottam a feladványt. (10. ábra)
Ennek a néhány mintának az alkalmazása igen hatékony tud lenni, ám közel sem old meg minden problémát, amivel szembekerülünk. Vannak olyan esetek, amikor egyszerűen nem lehet eldönteni, hol van az akna (ilyenkor nincs mit tenni, tippelnünk kell), és van, amikor ötletesebb, gondolkodósabb módszereket kell alkalmazni. Ezek azonban bonyolultabbak annál, hogy egy ilyen esszében könnyedén leírhatóak legyenek, és sokszor nem is eléggé „megfoghatóak”, mert csak a tapasztalt játékosok fejében léteznek.
Az emberi játékosok stratégiáiról térjünk most át arra, mihez kezdhet egy program egy aknakereső-táblával! Ehhez először a számítástudomány egyik fontos fogalmát kell megismernünk.
Az [1] oldalon további stratégiai tanácsok találhatóak, melyekből kiderül, hogyan érdemes tippelni, ha nem egyértelműen megoldható a tábla.
Az NP problémák az eldöntési problémák (olyan problémák, amelyekre egyetlen igen/nem válasz adható) egy igen érdekes és fontos osztályát alkotják. Az ebbe az osztályba tartozó problémák egy részének megoldására ugyan jelenleg nem ismert polinomiális idejű algoritmus, ám mindegyikhez létezik „pozitív tanú” algoritmus, azaz olyan polinomiális algoritmus, amely egy megfelelő „bizonyíték” alapján az „igen” választ ellenőrizni tudja. Példa erre a Hamilton-kör létezésének problémája: jelenleg nem ismert polinomiális idejű algoritmus annak meghatározására, hogy van-e egy gráfban Hamilton-kör, de egy konkrét Hamilton-kört bizonyítéknak használva polinomiális időben ellenőrizhető, hogy az tényleg kielégíti a feltételeket. Igen sok fontos NP-beli probléma van, ezek közé tartozik a már említett Hamilton-kör létezésének problémája, ill. például annak vizsgálata, hogy egy gráfban létezik-e k elemű független ponthalmaz.
Az NP-beli problémák egy kitüntetett csoportját alkotják az ún. NP-teljes problémák. Ezek olyan NP problémák, amelyekre bármelyik másik NP probléma polinomiálisan visszavezethető. Emiatt, ha valakinek valaha sikerül polinomiális idejű algoritmust adni egy NP-teljes probléma megoldására, azzal egy csapásra polinomiális időben megoldhatóvá teszi az összes NP-beli problémát. Az amerikai Clay intézet 2000-ben egymillió dolláros díjat tűzött ki annak, aki megold egy NP-teljes problémát polinomiális időben, vagy bebizonyítja, hogy ez lehetetlen.
A bizonyítás a [2] cikkben található, ám az nem elérhető az Interneten. A bizonyítás elvét és az áramköri elemek megvalósításának egy részét a [3] és [4] oldalakról szerezetem, egy részét (és a NOR-kapu bizonyítását) én dolgoztam ki.
Richard Kaye 2000-ben bebizonyította, hogy egy aknakereső-tábla konzisztenciájának ellenőrzése NP-teljes. A bizonyítás során egy ismerten NP-teljes problémát, az ún. SAT problémát (egy logikai formula kielégíthetőségének vizsgálata) vezette vissza az aknakereső-tábla konzisztenciájára. A visszavezetés során a kielégítendő logikai kifejezést először logikai áramkörré alakítjuk, majd az egyes komponenseket (kapuk, vezetékek, vezeték-metszések, kanyarok) megfelelő aknakereső-táblarészletekkel helyettesítjük. Ha az aknakereső-áramkört ki tudjuk tölteni aknákkal úgy, hogy a „kimenetén”, azaz egy megjelölt mezőben igaz érték (azaz akna) legyen, és a kitöltés ellentmondásmentes, akkor a logikai formula kielégíthető. Ha viszont az aknakereső-áramkör nem tölthető ki, akkor inkonzisztencia van jelen, tehát nem kielégíthető az eredeti logikai formula.
A bizonyítás alapvető irányvonalai után lássuk az egyes ekvivalenseket!
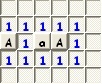
Az első alkatrész, amire szükségünk van, az egyenes (vízszintes) vezeték:
Látható, hogy a kék pöttyel jelölt „kimeneten” akkor és csak akkor van akna, ha a pirossal jelölt bemeneten akna van.
Részletesebb magyarázattal az alábbi ábra szolgál:
Ha a legbaloldalibb kérdéses négyzeten akna van, akkor a mellette lévőn biztosan nincs, mert különben a pirossal jelölt 1-esnek túl sok akna szomszédja lenne. Hasonlóan, ha nincs ott akna, akkor a szomszédján kell lennie. Azaz a két mező „akna-állapota” épp ellentétes: ha az egyiken akna van, akkor a másikon nincs, és fordítva. Ezt úgy jelöljük, hogy az egyik mezőbe „A”-t, a másikba „a”-t írunk. Ezt a jelölést a továbbiakban is használni fogjuk: a kis- és nagybetűk mindig ellentétes állapotú mezőket jelölnek, a különböző betűk pedig független mezőket. Az ábrát tovább töltve láthatjuk, hogy a vezeték két végén tényleg ugyanolyan állapotú mezők vannak.
Mivel időnként minden kapcsolási rajzban meg kell törnünk a vezetéket, szükségünk van „kanyar” elemre is, azaz olyan elemre, amihez egy vízszintes és egy függőleges vezeték csatlakoztatható, és a kimenetén ugyanaz az érték jelenik meg, mint a bemenetén. Egy lehetséges megvalósítás látható a 13. ábrán.
Előfordulhat, hogy felesleges vezetékvégek vannak az ábrán, amiket le kell zárni. A 14. ábrán látható összeállítás pirossal jelölt bemenetén mindegy, hogy van-e akna, mindkét esetben érvényes, ellentmondásmentes állapotot kapunk, így használható a szabad vezetékvégek
lezárására.
Szükségünk lehet arra is, hogy egy jelet két-, vagy akár háromfelé osszunk, erre nyújt lehetőséget a 15. ábrán látható „splitter” elem (ha csak kétfelé akarunk ágazni, az előbb bevezetett lezáró elemmel megoldhatjuk a problémát).
Kapcsolási rajzokon előfordul, hogy két vezeték metszi egymást, ennek megoldására a 16. ábrán látható táblarészletet használhatjuk fel. Látható, hogy a piros körrel jelölt bemenet értéke a kék körrel jelölt kimenetre kerül, a piros négyzettel jelölt a kék négyzettel jelöltre, egymástól függetlenül.
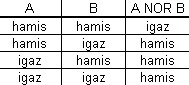
Az utolsó szükséges, és egyben legbonyolultabb áramköri elem a NOR (nem-vagy, sem-sem) kapu, aminek a megvalósítása a 17. ábrán látható (pirossal jelölve a bemenetek, kékkel a kimenet). A működés bizonyításához végezzük el az áramkör analízisét (egyelőre pár új ismeretlent bevezetve)! A NOR kapu elvi igazságtáblája a 19. ábrán látható.
Vizsgáljuk meg, milyen következtetéseket vonhatunk le, ha a két bemeneten „hamis” logikai értéket adunk az áramkörre, azaz ha az A-val és B-vel jelölt mezőkön nincs akna, az a-val és b-vel jelölteken pedig van! Ahhoz, hogy a 18. ábrán piros háttérrel megjelölt 4-es mellett 4 akna helyezkedjen el, muszáj, hogy a P-vel, Q-val és R-el jelölt mezőkön is legyen akna. A sárga hátterű 3-asok vizsgálatával könnyen belátható, hogy ekkor az y-nal és v-vel jelölt mezőkön lesznek még aknák, az u-val és x-szel jelölteken pedig nem lesznek, és a kapott állás ellentmondásmentes. Azt kaptuk tehát, hogy ha a két bemenet egyikén sincs „igaz” jel, akkor a kimeneten „igaz” jelet kapunk, tehát ebben az esetben a kapu jól működik.
Vizsgáljuk meg, milyen következtetést tudunk levonni abból, ha a kimenet „igaz” állapotú, azaz az R jelű mezőkön van, az r jelű mezőkön pedig nincs akna! Ebben az esetben a sárga hátterű 3-asokat megvizsgálva azt kapjuk, hogy a v-vel, Q-val, y-nal és P-vel jelölt mezőkön muszáj aknának lennie. A piros hátterű 4-est vizsgálva láthatjuk, hogy már „megvan” mind a négy aknája, így az A és B jelű mezőkön, azaz a bemeneteken semmiképpen sem lehet akna. Az u és x jelű mezőknek „hamis” (aknátlan) értéket adva egyértelmű, ellentmondásmentes állapotot kaptunk.
Az előző két bekezdés során kiderült, hogy ha a kapu bemenetére két „hamis” értéket kapcsolunk, akkor a kimenete „igaz” lesz, és ha a kimenet „igaz”, akkor a bemeneten biztosan két „hamis” érték van. Ennek a jellemzésnek a kétváltozós logikai függvények közül kizárólag a NOR felel meg, így az ábrán látható összeállítás valóban egy NOR kaput valósít meg.
Ismert, hogy NOR kapuk és vezetékek segítségével tetszőleges logikai függvényt megvalósító áramkör felépíthető. Ha a SAT problémában szereplő logikai függvényt megvalósítjuk egy áramkörrel, majd az áramkör egyes komponenseit az aknakereső-ekvivalenseikkel helyettesítjük, az áramkör bemeneteire „záró” áramkört, kimenetére pedig a 20. ábrán látható „konstans igaz” elemet tesszük, olyan aknakereső-táblát kapunk, amelynek konzisztenciája ekvivalens a logikai formula kielégíthetőségével. Mivel az ekvivalens generálása polinomiális ideig tart, és egy állítólag kielégítő aknaelrendezés ellenőrzése is polinom idejű, a probléma valóban NP-teljes.
Az aknakereső játék megoldása (azaz annak eldöntése, melyik mezőkön van biztosan akna, és melyikeken nincs biztosan) modellezhető kényszer-kielégítési problémaként (CSP, constraint satisfaction problem). Az ilyen problémák leírása során megadunk néhány változót, azok értékkészletét (lehetséges értékeit), valamint a változókra vonatkozó kényszereket. A feladat az, hogy meghatározzuk a változók összes olyan értékét, amelyek kielégítik a kényszereket.
Modellezzük az aknakereső játékot a következőképpen: a tábla i. sorának j. mezőjéhez rendeljünk egy xij változót, aminek értékkészlete a {0, 1} halmaz. A tábla minden mezőjére írjunk fel egy kényszert az alábbi módon:
-
ha az (i,j) mező biztonságos (vagy felfedett), vegyük fel az xij=0 kényszert
-
ha az (i,j) mező megjelölt, vegyük fel az xij=1 kényszert
-
ha az (i,j) mező felfedett, vegyünk fel egy olyan kényszert, ami a vele szomszédos üres és megjelölt mezőkhöz tartozó változók összegére előírja a mező aknaszámának értékét
Ha a kapott CSP-t kielégítő minden megoldásban xij=0, akkor az (i,j) mező biztosan biztonságos. Ha az összes megoldásban xij=1, akkor a mezőn biztosan akna van.
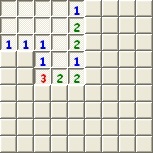
A következőkben bemutatok egy példát, hogy hogyan fogalmazhatunk át egy aknakereső-problémát CSP problémává. Tekintsük a 21. ábrán látható aknakereső-táblát!
Felírva a kényszereket (a triviális, xij=0 alakúakat kihagyva):
|
Mező |
Kényszer |
|
(1,5) |
x16+x26=1 |
|
(2,5) |
x16+x26+x36=2 |
|
(3,5) |
x26+x36+x46=2 |
|
(4,5) |
x36+x46+x56=1 |
|
(5,5) |
x46+x56+x66+x65+x64=2 |
|
(5,4) |
x63+x64+x65=2 |
|
(5,3) |
x42+x52+x62+x63+x64=3 |
|
(4,3) |
x42+x52=1 |
|
(3,3) |
x42=1 |
|
(3,2) |
x41+x42=1 |
|
(3,1) |
x41+x42=1 |
Egy lehetséges megoldás lépései:
-
A (2,5) és (1,5) egyenletek különbségéből következik, hogy x36=1, azaz (3,6) biztosan akna.
-
Az (5,5) és (5,4) egyenletek különbségéből következik, hogy x46+x56=0, és mivel minden változó pozitív, következik, hogy (4,6) és (5,6) biztonságos.
-
A (3,3) egyenletből következik, hogy (4,2) biztosan akna.
-
A (3,2) és (3,3) egyenletek különbségéből következik, hogy x41=0, azaz (4,1) biztonságos.
-
A (4,3) és (3,3) egyenletek különbségéből következik, hogy x52=0, azaz (5,2) biztonságos.
-
Tudjuk, hogy x46=0 és x36=1, így a (3,5) egyenlet alapján következik, hogy x26=1, azaz (2,6) biztosan akna.
-
Az előző pontból és az (1,5) egyenletből következik, hogy x16=0, azaz (1,6) biztonságos.
A korábbi következtetéseket grafikusan ábrázolva a 22. ábrán láthatók.
A fenti típusú CSP problémák megoldására találhatunk módszereket az [5] cikkben, amely azt is bemutatja, hogyan lehet hatékonyan meghatározni a nem egyértelmű változók értékének valószínűségi eloszlását.
[1] Sean Berett: Minesweeper: Advanced Tactics (http://nothings.org/games/minesweeper/
)
[2] Richard Kaye: Minesweeper is NP-complete. The Mathematical Intelligencer, 22(2):9–15, 2000.
[3] Richard Kaye's Minesweeper page (http://web.mat.bham.ac.uk/R.W.Kaye/minesw/minesw.htm
)
[4] Minesweeper is NP-complete (http://sed.free.fr/complex/mines.html
)
[5] Raphael Collet: Playing the Minesweeper with Constraints, Multiparadigm Programming in Mozart/Oz, Springer Lecture Notes in Computer Science, 2005, Volume 3389/2005, 251-262 (http://www.springerlink.com/content/l0cxhkuwv5edjpc0/fulltext.pdf
)
Szerző: Peregi Tamás, BME
Az alábbi ábra az 5 x 5 sakktáblán mutatja az N-királynő problémának a megoldását a tankönyvben említett tömörített állapottérreprezentáció mellett (oszloponként egy-egy királynőt helyezünk szabad helyre, balról jobbra haladva).

Készítette: Hegedűs Máté, BME
Közismert, hogy a játék állapottere particionált és két, azonos méretű állapottérből tevődik össze, amely részek között legális lépéssel átjárás nincs. Ez volt a játék hírnevét megalapozó kiirt verseny titka.
Az alábbi ábrán a minimalista 2 x 2 (3-puzzle) elrendezést vizsgálunk és tapasztalhatjuk az állapottér említett tulajdonságát.
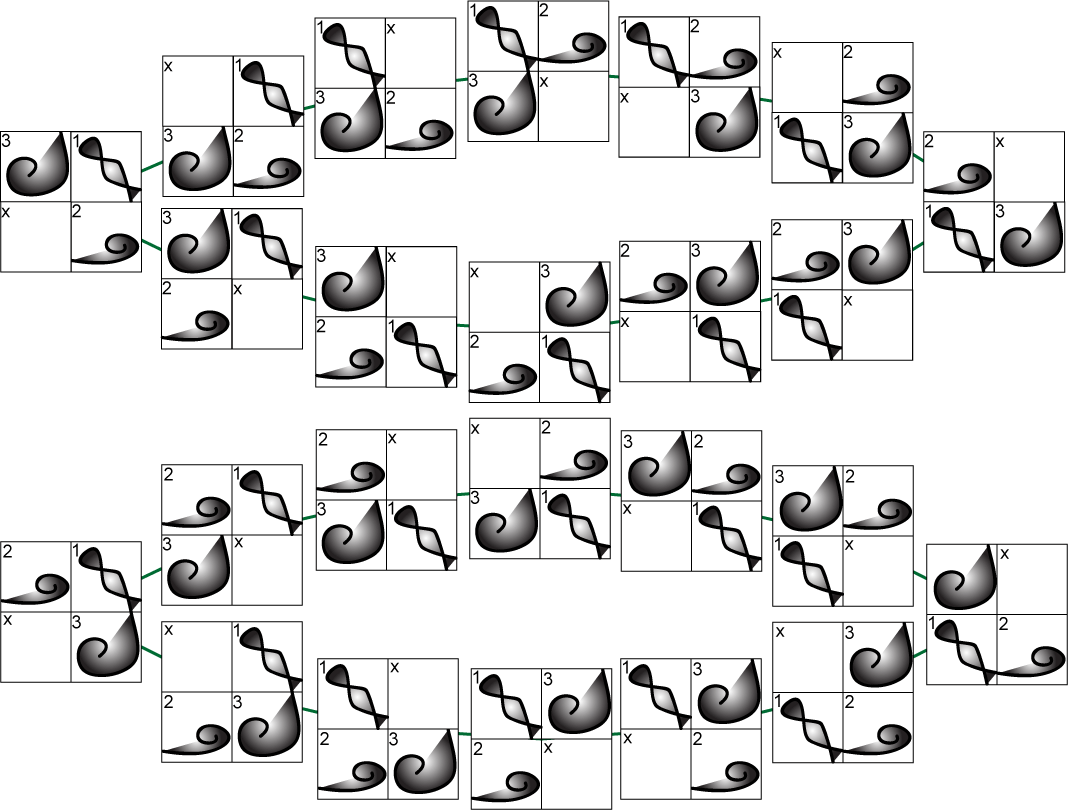
Készítette: Hegedűs Máté, BME






![4.1. táblázat. N-királynő probléma megoldásainak száma és ideje [13]](/mi_almanach/sites/default/files/books/257/files/kepek/8570/nqueenstable1.jpg)
![4.2. táblázat. N-királynő probléma backtrack megoldásainak lépésszáma [14]](/mi_almanach/sites/default/files/books/257/files/kepek/8570/nqueenstable2.jpg)