3.1. Problémamegoldó ágensek

3.1.1. Keresésről általánosan (BME)

A feladat célkitűzése:

A feladat célja azt gyakorolni, hogyan lehet egy feladatot, látszólagos hiányos információ mellett, a hiedelmi állapottérben megfogalmazni és ott szisztematikusan megoldani.

A feladat leírása, kérdések:

Egy ősi kriptában egy oszlopot találunk, négy, egy magasságban, szimmetrikusan elhelyezett nyílással, amibe épp a kezünk fér bele. Az ősi írás az oszlopon elmondja, hogy az oszlop a kincses kamrát nyitó mechanizmus része. Minden nyílás mélyén egy kapcsoló el van rejtve, mely „fel”, vagy „le” állásban lehet. Ha mind a négy kapcsoló azonos állásban lesz, a kincses kamra ki fog nyílni. Az oszlop elegendően kicsi, hogy át lehessen ölelni, két kézzel tehát tetszőleges kapcsolópárhoz férhetünk hozzá egyszerre.

Azonban, ahogy valamelyik kezünket a nyílásból kivesszük, az oszlop forogni kezd és a véletlen számú negyed fordulat megtételével áll csak meg. Egyidőben tehát két kapcsoló állását megváltoztathatjuk, majd mindkét kezünket egyszerre rántjuk ki. Milyen stratégiát eszelhetünk ki a kincses kamra véges és kicsi számú lépésben történő kinyitásához? Tételezzük fel, hogy a forgás után a nyílások identitása külsőleg nem különböztethető meg.

3.1.1-1. ábra - „The Secret Chamber” by Kevin J. Lin, http://www.greylabyrinth.com/puzzle/puzzle102 felhasználásával

A feladat megoldása

A megoldás lényege:

Mivel a négy kapcsoló közül csak kettőt tudunk érzékelni, ill. állítani, valamint mivel az oszlop véletlen pörgése miatt a kapcsolók identitása nem memorizálható a következtetés számára, a probléma állapotterét „normális” egyedi állapototkból és operátorokból nem építhetjük fel. Egyetlen remény a hiedelmi állapottér használata, abban bízva, hogy benne úgy sikerül a feladatot megfogalmazni, hogy kimutatható módon létezik egy megoldási pálya a kezdeti és a cél állapot között.

Részletes megoldás:

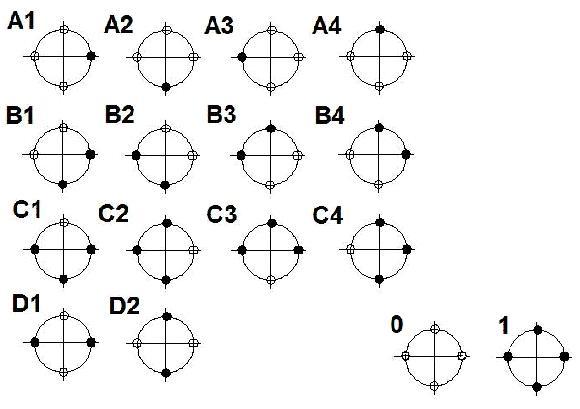
Kiséreljük feltérképezni a nem mindig érzékelhető, de valódi környezeti állapotokat. Itt nemcsak az oszlopot kell modelleznünk (hány kapcsoló van „fel” állapotban), de az ágenst is (azaz inkább a szenzorikus apparátusát, amivel csak meghatározott konfigurációban meg tudja vizsgálni a kapcsolók állapotát). Az „A” állapotokban tehát egyetlenegy kapcsoló van felkapcsolva, és az állapotok számozása megkülönbözteti annak fekvését az ágensre nézve akkor, amikor kezeinek benyulásával meg szeretne róla győződni. Az alábbi ábrán feltüntettük az összes állapotot (felkapcsolt kapcsoló: fekete, lekapcsolt: fehér). A „0” és „1” állapotok a kamrát nyító oszlopállapotok.

Az ágens természetesen annyira pontosan az állapototkat megkülönböztetni nem tudja. Jelöljük a hiedelmi állapotait a következő módon:

(A, B, C, D) - ágens legfeljebb azt tudja, hogy az állapot az A, B, C, vagy D típusú állapotok valamelyike.

(B, D, 1) – az állapot a B, vagy D típ. Állapot, illetve a nyító állapot, de ha múlik az idő és a kamra mégsem nyílik, akkor az ágensnek rá kell jönnie, hogy az állapot csak (B, D) lehet.

(A1, B2) - konkrétabb, és az A1 ill. B2 állapotok valamelyikét jelenti, stb.

A kezdő állapot a „semmit sem tudok” állapot, azaz

(A, B, C, D) = (A1, A2, ..., A4, B1, ..., B4, ...., D2),

és a célállapot (0), (1), vagy (0, 1) állapotok egyike.

Most modellezni kellene az ágens cselekvéseit. Erre több lehetőség kínálkozik. Mivel a feladat leírása alapján ágensnek, a kezével a nyílásba benyúlva, lehetősége van érzékelni a kapcsolók állását és ennek alapján eldönteni, hogyan kapcsolja azokat át, mindenképpen IF ... THEN ... ELSE ... cselekvés-sémában kellene gondolkodnunk. A négy nyílásba két kézzel egyszerre többféle módon nyúlhatunk bele, de itt szerencsére a pörgés egyszer a segítségünkre is lesz, mert a feladatban egyfajta szimmetriát vezet be.

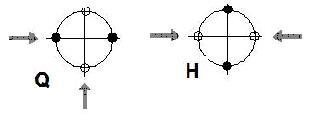
Az oszlopba tehát vagy „Q”, vagy „H” konfigurációban nyúlhatunk bele két kézzel. Az ágens cselekvése tehát:

IF Érzékelés THEN Kapcsolgatás1 ELSE Kapcsolgatás2

de lehetne egyszerűbben is:

IF Érzékelés THEN Kapcsolgatás

ahol az érzékelés lehet:

QFF: mindkét kapcsolót Q konfigurációban „fel” állásban érzékeljük,

QFL: bal kapcsolót „fel”, inneső kapcsolót „le” állásban érzékeljük

QLF, QLL hasonlóképpen.

HFF, HFL, HLF, HLL u.a. H konfigurációban

NOP: semmi lényegest nem érzékelünk

Rövidítés gyanánt bevezethetjünk változókat is: pl. QXY.

A kapcsolgatás konvenciója hasonló, azaz QFF azt jelenti, hogy Q konfigurációban mindkét kapcsolót „fel” állásba kapcsoljuk. stb., illetve változókkal kifejezve, pl.: Q~XY azt jelenti, hogy az érzékelés alapján a baloldali kapcsolót átkapcsoljuk, az innensőt pedig nem bátjuk.

Az érzékelés persze nem tökéletes (és ebben van a feladat egész nehézsége). Az alábbi ábrán láthatjuk pl. az IF HXY ... cselekvéssel nem megkülönböztethető állapotokat.

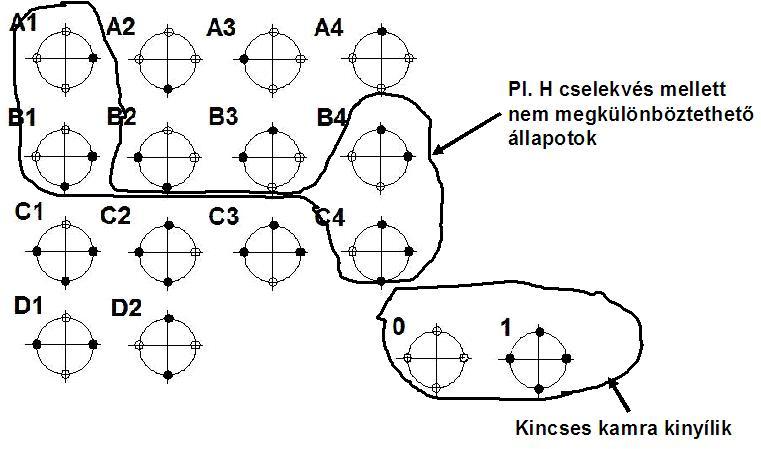
Megállj! Remek ötletünk van! Mi lenne, ha egyszerűen IF NOP THEN HFF módon lépnénk, és ha a kamra nem nyílik, ugyanazzal a lépéssel folytatnánk tovább? Hiszen a két átellenes kapcsolót felkapcsoljuk, és ha a pörgés miatt a másik két kapcsolót is elkapjuk, akkor a kamra ki fog nyílni.

Persze, ha a pörgés a kapcsolókat véletlenül pont ugyanabba a pozicióba állítja újra, amit már lekezeltünk, az újbóli kapcsolgatásnak hatása nem lesz. De előbb-utóbb csak másképpen áll be az oszlop, ugye? Jó uton járunk tehát, vagy sem?

Az eset annak felel meg, hogy akkor nyerünk egy érmedobás sorozatban, ha fej mellett lesz benne írás is. A vesztes sorozat a fej, fej, fej, ..., fej, ... és így végtelenségig. Tudjuk, hogy egy ilyen sorozat valószínűsége rohamosan 1/2^N szerint csökken, de valószínűségről akkor beszélgethetünk, ha a hasonló problémamegoldást többször (igen sokszor) megismételhetjük. Ha csak egyetlenegy próbáról van szó (mert pl. nem a kincses kamra nyílik, hanem élelem nélkül egy kamrába be vagyunk zárva, minden kisérlettel apad az erőnk, és az életünk múlik a gyors kiszabaduláson), akkor bezzeg egy ritka esemény is meg tud fordulni, mi pedig porul fogunk járni.

Sőt, egy ilyen katasztrofális sorozat valószínűsége akár 1 is lehetne, ha az oszlopon belüli pörgési mechanizmus nem lenne ideális, és pl. az excentricitása miatt mindig ugyanúgy állna be.

Jobb lenne tehát egy (idő)biztos megoldás, ami minden körülmény közt működik és garantáltan véges számú lépést fog kezünkbe adni.

Térjünk vissza tehát a hiedelmi állapottérbe. Tudjuk már, mik benne az állapotok, mik a legális cselekvések. Fel kellene most mérni a várható elágazási tényezőt, a megoldás mélységét, megfontolni a szóba jöhető heurisztikákat és cselekvésköltségeket, és ennek alapján a keresési algoritmus jellegét.

Minél rövidebb megoldást szeretnénk, a különféle kézbenyúlás között a nehézségekben különbséget nemigen tudnánk tenni, a pörgés miatt fogalmunk sem lehet, mennyire már haladunk előre, stb. ez mind inkább a szélességi keresésre vall. Mennyire nehéz lesz? Mennyi az elágazás?

IF Érzékelés THEN Kapcsolgatás1 ELSE Kapcsolgatás2

A lehetséges redundáns megfogalmazással nem törődve a cselekvésstruktúra kettő lehet Q, vagy H; az érzékelés lehet 6-féle (NOP, LL, LF, FL, FF, XY) ; minden kapcsolgatás lehet 8-féle (NOP, LL, LF, FL, FF, ~XY, X~Y, ~X~Y). A lehetséges legális lépések számát:

b = 2 x 6 x 8 = 96

számmal majorizálhatjuk. A triviális redundáns (semmit nem változtató) lépések kiszűrése természetesen ezt a számot erőteljesen mérsékli (mennyire?), de a szélességi keresés komplexitása akkor is magas lehet, főleg, ha a megoldás mélységéről egyáltalán nincs elképzelésünk (emlékezzük, hogy szélességi keresés időben és tárban exponenciális, O(b^d)).

Megjegyzés: az állapotok és a cselekvések rögzítése problémateret definiál, amiben keresni fogunk. Egy konkrét valós problémához több absztrakt problémateret is szerkeszthetünk (itt pl. az előbb említett különböző cselekvésformátum megválasztásával). A lényeg, hogy ezek az absztrakt terek jól fejezzék ki a valós probléma lényegét, hogy lehessen bennük keresni, és hogy a megkeresett megoldást lehessen a valódi problémára sikerrel alkalmazni (ld. a keresés, problématér fogalmi körét, 3.1 fejezet).

De mindenképpen annyiban sínen vagyunk, hogy van elvi módszerünk, ami a megoldást (ha van) garantáltan megkeresi, csak most már nem elég a két kezünk, számítógép is kell hozzá.

Tegyük fel, hogy a társunk foglalkozik már a programozással, mi pedig, gyanút fogva, hogy a probléma hátrafelé szemlélve esetleg mérsékeltebb elágazási számot mutat, nekiesünk a cél állapot felül megfontolni a megoldást.

Használjuk a következő cselekvési szabályokat:

(NOP, kapcsolás),

(absztrakt érzékelés, absztrakt kapcsolás)

(konkrét érzékelési minta, kapcsolás, érzékelési minta beállítása)

Az állapotér jobb, manuális feltérképezése végett készítsük az alábbi táblázatot, ahol egy-egy sor annak felel meg, hogy az első oszlopban feltüntetett cselekvés a többi oszlopot megcímkéző állapotból milyen hiedelmi állapotot eredményez. A táblázat alapján képet kaphatunk arról, hogy egy cselekvés adott hiedelmi állapotból milyen hiedelmi állapotba vezet át. Ehhez a cselekvés sorában össze kell másolni azoknak az oszlopoknak a tartalmát, amelyek együtt a kiinduló hiedelmi állapotot adják ki. A (NOP, QLL) cselekvés pl. a kezdeti (A, B, C, D) állapotból a (0, A, B) állapotba vezet, amely – ha a kamra mégsem nyílik meg és a pörgés megtörténik – egy (A, B) állapottal lesz ekvivalens. A táblázat ily módon, implicite, a keresési tér állapotgráfját ábrázolja.

A hátrafelé keresést a célállapotok egyikéből kell indítani. Látunk egy ilyen állapotot – (0, 1) - a táblázat három sorában, utolsó oszlopában. A táblázat egyben azt is jelzi, hogyha a probléma absztrakt megfogalmazásában csakis a zöld színnel jelölt konkrét megfogalmazású cselekvések használatára korlátoznánk, a probléma nem oldható meg (a tiszta célállapot nem érhető el) és a kezdeti hiedelmi (A, B, C, D) állapotból indított szélességi keresés az exponenciális problémák miatt belefullad, mégsem talál rá megoldásra. Ugyanúgy meddő lenne megkísérelni a (0), vagy az (1) célállapotok elérését, hiszen nem is szerepelnek az állapotok között.

A feltételes módon megfogalmazott absztrakt cselekvések felvétele a probléma megfogalmazásába tehát nemcsak kényelmi szempont, másképpen nem megy.

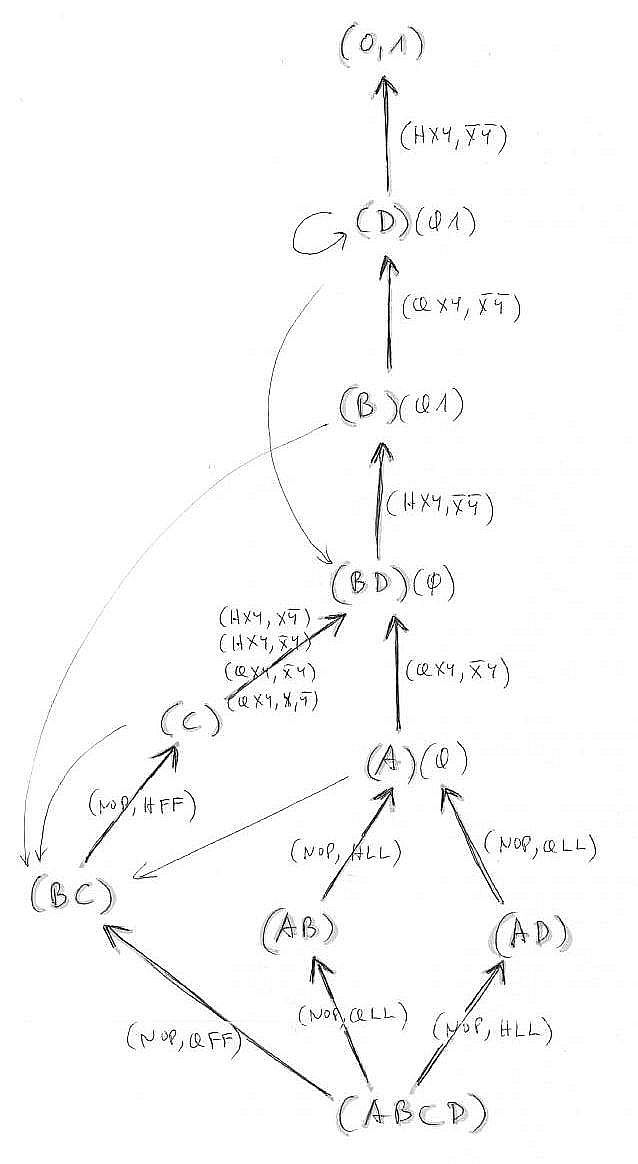
A táblázatból látjuk, hogy a (0, 1) hiedelmi célállapot (HXY, H~X~Y) cselekvéssel (D) állapotból áll elő és semmi másból. A hátrafelé való keresésénél az elágazási tényező a cél közelében tehát 1! A (D) állapotot a (B) állapot oszlopában találjuk, (QXY, Q~X~Y) cselekvés sorában. A (B) állapotot, enyhe ügyeskedéssel, (0, 1, B)-ig kiterjesztve (B, D) állapot felül érhetjük el (HXY, H~X~Y) cselekvéssel. A (B, D) állapot (0, B, D) változatában az (A) állapotból több cselekvéssel is elérhető. Válasszuk ehhez pl. (QXY, Q~XY)-t. Az (A) állapot, (0, A)-ra kiegészítve, elérhető (A, B)-ből (NOP, HLL) révén, vagy (A, D)-ből (NOP, QLL) révén. Az (A, B), ill. az (A, D) viszont pont fordított cselekvések alkalmazásával már a kezdeti (A, B, C, D) állapotból érhető el. A mellékelt ábra (Secret4sh.jpg) mutat még egy lehetőséget (B, C) – (C) állapotokon keresztül.

A teljes megoldás tehát 6 lépésből áll:

(A,B,C,D) állapotban (NOP, HLL) cselekvés, ami (A,D,0) állapotba vezet:

tehát a kamra vagy kinyilik, vagy tudjuk, hogy az

újbóli forgás után az (A, D) állapotban leszünk.

(A,D) állapotban (NOP, QLL) cselekvés, ami (A,0) állapotba vezet:

tehát a kamra kinyilik, vagy tudjuk, hogy az (A) állapotban leszünk.

(A) állapotban (QXY, Q~XY) cselekvés, ami (B,D,0) állapotba vezet:

tehát, ha a kamra nem nyilik, (B,D)-vel folytatjuk.

(B,D) állapotban (HXY, H ~X~Y) cselekvés, ami (B,0,1) állapotba vezet:

tehát, ha a kamra nem nyilik, (B)-vel folytatjuk.

(B) állapotban (QXY, Q~X~Y) cselekvés, ami (D,0,1) állapotba vezet:

tehát, ha a kamra nem nyilik, (D)-vel folytatjuk.

(D) állapotban (HXY, H~X~Y) cselekvés, ami (0,1) állapotba vezet:

és a kamra kinyílik, ha korábban mégsem.

	A	B	C	D
NOP, QLL	0A	0AB	AB	A
NOP, QLF	ABD	ABCD	BCD	BD
NOP, QFL	ABD	ABCD	BCD	BD
NOP, QFF	BC	1BC	1C	C
NOP, HLL	0A	A	AD	0D
NOP, HLF	AB	B	BC	AC
NOP, HFL	AB	B	BC	AC
NOP, HFF	CD	C	1C	1D
QLL, QLF	0BD	0AC	AB	A
QLL, QFL	0BD	0AC	AB	A
QLL, QFF	0C	01A	AB	A
QLF, QLL	0ABD	ACD	BCD	AB
QLF, QFL	ABD	ACD	BCD	B
QLF, QFF	ABD	ACD	1BCD	BC
QFL, QLL	0ABD	ACD	BCD	AB
QFL, QLF	ABD	ACD	BCD	B
QFL, QFF	ABD	ACD	1BCD	BC
QFF, QLL	BC	01C	1A	C
QFF, QLF	BC	1AC	1BD	C
QFF, QFL	BC	1AC	1BD	C
HLL, HLF	0B	A	AD	0C
HLL, HFL	0B	A	AD	0C
HLL, HFF	0C	A	AD	01
HLF, HLL	0AB	AB	BCD	AC
HLF, HFL	AB	B	BC	AC
HLF, HFF	ABD	BC	1BC	AC
HFL, HLL	0AB	AB	BCD	AC
HFL, HLF	AB	B	BC	AC
HFL, HFF	ABD	BC	1BC	AC
HFF, HLL	CD	C	1A	01
HFF, HLF	CD	C	1B	1A
HFF, HFL	CD	C	1B	1A
QXY, Q~XY	0BD	AC	1BD	AC
QXY, QX~Y	0BD	AC	1BD	AC
QXY, Q~X~Y	AC	01D	AC	B
HXY, H~XY	0BD	AC	1BD	AC
HXY, HX~Y	0BD	AC	1BD	AC
HXY, H~X~Y	AC	B	AD	01

Lehetséges-e ennél rövidebb megoldás? Figyeljük meg, hogy a (HFF, HFL) hatására (C)-ből (B2,B3,1)-be kerülünk, pörgés után tehát (B)-ben leszünk. (C)-t, pontosabban (C1, C3, 1)-t (NOP, HFF)-vel érjük el (B, C)-ből. (B, C)-t, pontosabban (B2,C1,C2,1)-t, (NOP, QFF)-vel érjük el a kezdeti (A, B, C, D) állapotból.

Az új megoldás tehát 5 lépéses szekvencia:

(A,B,C,D) állapotban (NOP, QFF) cselekvés, ami (B2,C1,C2,1) = (B,C,1) állapotba vezet:

tehát a kamra vagy kinyilik, vagy tudjuk, hogy az

újbóli forgás után a (B, C) állapotban leszünk.

(B,C) állapotban (NOP, HFF) cselekvés, ami (C1,C3,1), állapotba vezet:

tehát a kamra kinyilik, vagy tudjuk, hogy a (C) állapotban leszünk.

tehát, ha a kamra nem nyilik, (B)-vel folytatjuk.

(B) állapotban (QXY, Q~X~Y) cselekvés, ami (D1,D2,0,1) állapotba vezet:

tehát, ha a kamra nem nyilik, (D)-vel folytatjuk.

(D) állapotban (HXY, H~X~Y) cselekvés, ami (0,1) állapotba vezet:

és a kamra kinyílik, ha korábban mégsem.

Lehetséges-e azoknál rövidebb megoldás? Erre igazi választ mégis a szélességi keresésnek teljes körű lefuttatása jelentene, megfigyelve, hogy milyen szinten fut rá első ízben valamelyik (nem szükségképpen kizárólagosan (0, 1)-re) célállapotra (ill. a célállapotból indítva, a kezdeti állapotra).

Megállj! És mi a helyzet az előbb említetett excentrikus oszloppal? Mivel a hiedelmi állapottérben a keresés csakis a hiedelmi állapotok információtartalmához igazítja a legális cselekvéseket, és csakis e két információ (a hiedelmi állapot és a cselekvés tartalma) alapján számítja ki az eredményt, nem forog semmilyen veszélyben, hiszen a torz beállás miatt az állapotok információtartalma nem fog változni! Sőt! Elképzelhető, hogy a torzítás miatt a kívánt nyitó kapcsolókombináció még inkább korábban fog bekövetkezni.

Kidolgozta: Dobrowiecki Tadeusz, BME

3.1.2. A titkos kamra feladvány (BME)

Rövid szöveges leírás magyar nyelven

Látszólagos egyszerűsége ellenére keresés (valamilyen konkrét algoritmikus formában) intelligens ágensek legfontosabb algoritmusa. Azért is olvashatunk róla mindjárt a tankönyv elején, az ágens fogalmának bevezetése után, és ha a későbbi anyagban mintha nem is esne már róla szó, ne tévesszen ez minket. Intelligens viselkedés kutatása során kereséssel mindig, mindenhol fogunk találkozni, legfeljebb sokszor burkolt, elfedett formában.

Részletes szöveges bemutatás magyar nyelven

A keresés az un. keresési térben (vagy problématérben) történik és a feladata átvezetni az ágenst a tér egyik pontjából (kiinduló állapot, a probléma kiinduló állapota) a tér egy másik pontjába (cél állapot, a probléma megoldása). A keresés egy olyan intelligens tevékenység, ami a döntések sorozatából áll. Egy-egy döntés lényege, hogy az adott helyen szóba jöhető egyes cselekvési alternatívákról (akár csak ideiglenesen) lemondunk, elkötelezve magunkat azok mellett, amiktől fokozott előnyt, nyereséget várunk. Minél több az alternatíva (ezt elágazási tényezőnek nevezzük), annál nehezebb a döntés és annál súlyosabb következményei (keresés költségei) vannak annak, ha az információink netán nem teljesen pontosak. Szerencsével, ha a döntésünk megalapozott volt (jó volt az irányt súgó információ, avagy a heurisztika), a megválasztott alternatívák gazdagabb, pontosabb információhoz és más mérhető előnyökhöz juttatnak idővel minket. Az alternatívák feltárásával új döntési helyzetek teremtődnek. A döntési sorozat természetes beteljesülése, ha eljutunk oda, ahová kívánkoztunk (ezt cél állapotnak nevezzük, és a célállapotok elérésére törekvő ágenst racionálisnak mondjuk).

Keresési algoritmusok vizsgálatában alapvető különbséget jelent egyrészt, hogy a kereső (döntést hozó) ágens egy élő ágens (ember, állat, ...), vagy az emberi intelligencia megvalósítására megtervezett gépi ágens (szoftver program, vagy robot), másrészt az is, hogy a keresés milyen keresési térben történik. Ha az alternatívák feltárása fizikailag érzékelhető térben (légtér, erdő, város utcái, irodaház folyosói, stb.) történik, akkor a kereséssel valódi mozgás, ill. más fizikai hatás párosul. Keresünk utat, helyet, tárgyat, szerelünk órát, motort, polcon rendezünk könyveket, vagy spájzban befőttes üvegeket, …. A tér azonban lehet matematikai absztrakt tér, aminek kapcsolata a közvetlenül tapasztalt valósággal általában sokkal összetettebb. Ilyen terekben keresünk matematikai problémák megoldását, egy logikai állítás bizonyítását, egy feladatot megvalósító tervet. Az iIlyen absztrakt térben valósul meg szintén az ágens tanulási folyamata.

A döntések (keresési irányok) megválasztása több módon alakulhat. Néha fontos tudni visszakerülni egy korábbi döntési helyzetbe (ezt visszalépésnek nevezzük), hogy az utólag rendelkezésre álló információ birtokában jobb döntést hozhassunk. Néha a visszalépés túlságosan költséges, túl sok időt, energiát, anyagiakat igényel és célszerűbbnek tűnik a döntésekben csakis előre rohanni. A tér jellege nagyban befolyásolja, hogy pl. a visszalépés egyáltalán lehetséges, vagy felvállalható-e.

Fizikai térben ritkán szoktunk a kiindulási helyhez visszakerülni és más irányokkal próbálkozni, inkább előre törekszünk, bízva, hogy ha ez az út nem is a legjobb, mégis elvezett a célhoz (példának legyen akár egy turista, aki idegen városban valamilyen látványosságot keres). Vannak esetek azonban, amikor a keresési tér jellege miatt ajánlatos inkább visszalépni és egy korábban ki nem próbált elágazás mentén szerencsét keresni. Ilyen például a jelzett út elvesztése hegyvidéken, rossz időben.

Az élő és a gépi kereső ágens között talán az a legfontosabb különbség, hogy egy élő ágens nem szívesen vállalkozik a keresésben a nyers erő alkalmazására (azaz minden eshetőség megvizsgálására), akármennyire ez elvi garanciát biztosít a megoldás megtalálására. Egyszerűen kevés az idő, vagy szűkében van más fontos un. erőforrás, amit a nyers erő túlságosan felemésztene. Élő ágens keresési döntései feltétlenül támaszkodnak valamilyen irányt súgó információra, legyen ez egy színes folt a méhecskének, érdekes illatok a szimatoló kutyának, vagy utcanevek a házak sarkán turisták számára (egy ilyen irányt jelző információt heurisztikának és az azt felhasználó kereséseket informáltnak, vagy heurisztikusnak fogjuk nevezni, a nyers erőre támaszkodó un. vak, gyenge, vagy nem informált keresésekkel szemben). Irányt jelző információ elképzelhető absztrakt keresési terekben is. Gondoljuk itt pl. arra, hogy néhány példából általánosítva szeretnénk ágensünket a példák tömör definíciójára megtanítani, és abban az irányban folytatjuk (tanulási) térben a keresést, amerre a definíció tömörebben kezd alakulni (Ockham borotva elve).

Az előbbi megjegyzés egyenes következménye, hogy egy élő ágens igazából soha nem képes (de nem is törekszik erre) ideálisan optimális megoldást megtalálni. A ténylegesen legjobb megoldás megtalálásához a keresési teret rendszeresen, kimerítően végig kell nézni, aminek ódiuma össze-mérhető a nyers erő módszer nehézségeivel. Azt is szokás mondani, hogy az ember (és más élő ágens) majdnem (közel) optimális megoldásra törekszik, mert a valós életben ez az igazán kifizetődő.

Fizikai térben való keresés valódi cselekvéseket igényel, ami valódi veszélyeket is jelenthet, netán katasztrofális kimenetellel, ha ágens döntéseihez hiányos, vagy hibás információt használ (vajon mi történik, ha egy robot hibásan úgy ítéli, hogy egy híd el fogja bírni a súlyát és utat rövidítve megkísérel rajta átkelni?) Gépi ágens, nem fizikai térben keresve a keresési tér matematikai leírásában képes feltérképezni a lehetőségeket, képes büntetlenül visszalépni, rendelkezik végül elegendő számítási kapacitással a nyers erő alkalmazásához. Így akár ideálisan optimális megoldásokra is törekedhet.

Egy ügyes élő ágens azonban (ilyen az ember, de kutya, vagy méhecske már nem tud itt velünk lépést tartani) megtervezhet egy ügyes gépi ágenst, amire a keresési feladatát áthárítja. Ha a keresés absztrakt térben történik, elegendő megtervezni az gépi ágens szoftver belsejét, avagy programját, hiszen minden keresési lépés ágens tudásbázisában történik, az ágens csak „gondolkodik”, a keresés az ágens „fejében” történik. Fizikai térben való keresés esetén a helyzet annál bonyolultabb. Mivel a keresési lépések valóban, az ágenst körül vevő fizikai környezetben történnek, elvégzésükhöz valódi mechanizmusok és erőforrásokat szükségesek. Muszáj ilyenkor megtervezni az ágens fizikai küllemét, azaz architektúráját, aminek központi tervezési kérdése eldönteni, hogy az ágens milyen érzékelő és milyen végrehajtó szervekkel rendelkezzen a siker érdekében. Ha az áthárítás sikerül (képesek vagyunk a keresési tér matematikáját megalkotni, beprogramozni, architektúrát kialakítani, a számításokat kivárni, stb.), akkor majdnem optimális emberi voltunk ellenére is optimális megoldásokhoz juthatunk, amiket majd életbe léptetünk (ilyen pl. az gépkocsi útvonal kereső programok használata). Ilyen megoldásokra tanít minket a könyv.

Meg kell említeni végül, hogy a heurisztikus keresés, mint mechanizmus, központi szerepet foglal Allen Newell és Herbert Simon által javasolt un. fizikai szimbólumrendszer hipotézisben.

Kapcsolódó olvasmányok

Fizikai szimbolumrendszer hipotézisről:

[Newell, Allen; Simon, H. A. (1976), "Computer Science as Empirical Inquiry: Symbols and Search", Communications of the ACM, March 1976, Vol 19, No 3, pp. 113-]126 (1975 Turing Award Lecture)

http://portal.acm.org/citation.cfm?id=360022

http://en.wikipedia.org/wiki/Physical_symbol_system

http://www.rci.rutgers.edu/~cfs/472_html/AI_SEARCH/PhysicalSymbolSystemHyp.html

http://www.rci.rutgers.edu/~cfs/472_html/AI_SEARCH/PSS/PSSH1.html [ ]

Kidolgozta: Dobrowiecki Tadeusz, BME

3.1.3. Keresés rejtett fontossága (BME)

Áttekintés

Látszólagos egyszerűsége ellenére keresés (valamilyen konkrét algoritmikus formában) intelligens ágensek legfontosabb algoritmusa. Azért is olvashatunk róla mindjárt a tankönyv elején, az ágens fogalmának bevezetése után, és ha a későbbi anyagban mintha nem is esne már róla szó, ne tévesszen ez minket. Intelligens viselkedés kutatása során kereséssel mindig, mindenhol fogunk találkozni, legfeljebb sokszor burkolt, elfedett formában.

A keresés bemutatása

A keresés az un. keresési térben (vagy problématérben) történik és a feladata átvezetni az ágenst a tér egyik pontjából (kiinduló állapot, a probléma kiinduló állapota) a tér egy másik pontjába (cél állapot, a probléma megoldása). A keresés egy olyan intelligens tevékenység, ami a döntések sorozatából áll. Egy-egy döntés lényege, hogy az adott helyen szóba jöhető egyes cselekvési alternatívákról (akár csak ideiglenesen) lemondunk, elkötelezve magunkat azok mellett, amiktől fokozott előnyt, nyereséget várunk. Minél több az alternatíva (ezt elágazási tényezőnek nevezzük), annál nehezebb a döntés és annál súlyosabb következményei (keresés költségei) vannak annak, ha az információink netán nem teljesen pontosak. Szerencsével, ha a döntésünk megalapozott volt (jó volt az irányt súgó információ, avagy a heurisztika), a megválasztott alternatívák gazdagabb, pontosabb információhoz és más mérhető előnyökhöz juttatnak idővel minket. Az alternatívák feltárásával új döntési helyzetek teremtődnek. A döntési sorozat természetes beteljesülése, ha eljutunk oda, ahová kívánkoztunk (ezt cél állapotnak nevezzük, és a célállapotok elérésére törekvő ágenst racionálisnak mondjuk).

Keresési algoritmusok vizsgálatában alapvető különbséget jelent egyrészt, hogy a kereső (döntést hozó) ágens egy élő ágens (ember, állat, ...), vagy az emberi intelligencia megvalósítására megtervezett gépi ágens (szoftver program, vagy robot), másrészt az is, hogy a keresés milyen keresési térben történik. Ha az alternatívák feltárása fizikailag érzékelhető térben (légtér, erdő, város utcái, irodaház folyosói, stb.) történik, akkor a kereséssel valódi mozgás, ill. más fizikai hatás párosul. Keresünk utat, helyet, tárgyat, szerelünk órát, motort, polcon rendezünk könyveket, vagy spájzban befőttes üvegeket, …. A tér azonban lehet matematikai absztrakt tér, aminek kapcsolata a közvetlenül tapasztalt valósággal általában sokkal összetettebb. Ilyen terekben keresünk matematikai problémák megoldását, egy logikai állítás bizonyítását, egy feladatot megvalósító tervet. Az iIlyen absztrakt térben valósul meg szintén az ágens tanulási folyamata.

A döntések (keresési irányok) megválasztása több módon alakulhat. Néha fontos tudni visszakerülni egy korábbi döntési helyzetbe (ezt visszalépésnek nevezzük), hogy az utólag rendelkezésre álló információ birtokában jobb döntést hozhassunk. Néha a visszalépés túlságosan költséges, túl sok időt, energiát, anyagiakat igényel és célszerűbbnek tűnik a döntésekben csakis előre rohanni. A tér jellege nagyban befolyásolja, hogy pl. a visszalépés egyáltalán lehetséges, vagy felvállalható-e.

Fizikai térben ritkán szoktunk a kiindulási helyhez visszakerülni és más irányokkal próbálkozni, inkább előre törekszünk, bizva, hogy ha ez az út nem is a legjobb, mégis elvezett a célhoz (példának legyen akár egy turista, aki idegen városban valamilyen látványosságot keres). Vannak esetek azonban, amikor a keresési tér jellege miatt ajánlatos inkább visszalépni és egy korábban ki nem próbált elágazás mentén szerencsét keresni. Ilyen például a jelzett út elvesztése hegyvidéken, rossz időben.

Az élő és a gépi kereső ágens között talán az a legfontosabb különbség, hogy egy élő ágens nem szívesen vállalkozik a keresésben a nyers erő alkalmazására (azaz minden eshetőség megvizsgálására), akármennyire ez elvi garanciát biztosít a megoldás megtalálására. Egyszerűen kevés az idő, vagy szűkében van más fontos un. erőforrás, amit a nyers erő túlságosan felemésztene. Élő ágens keresési döntései feltétlenül támaszkodnak valamilyen irányt súgó információra, legyen ez egy színes folt a méhecskének, érdekes illatok a szimatoló kutyának, vagy utcanevek a házak sarkán turisták számára (egy ilyen irányt jelző információt heurisztikának és az azt felhasználó kereséseket informáltnak, vagy heurisztikusnak fogjuk nevezni, a nyers erőre támaszkodó un. vak, gyenge, vagy nem informált keresésekkel szemben). Irányt jelző információ elképzelhető absztrakt keresési terekben is. Gondoljuk itt pl. arra, hogy néhány példából általánosítva szeretnénk ágensünket a példák tömör definíciójára megtanítani, és abban az irányban folytatjuk (tanulási) térben a keresést, amerre a definíció tömörebben kezd alakulni (Ockham borotva elve).

Az előbbi megjegyzés egyenes következménye, hogy egy élő ágens igazából soha nem képes (de nem is törekszik erre) ideálisan optimális megoldást megtalálni. A ténylegesen legjobb megoldás megtalálásához a keresési teret rendszeresen, kimerítően végig kell nézni, aminek ódiuma össze-mérhető a nyers erő módszer nehézségeivel. Azt is szokás mondani, hogy az ember (és más élő ágens) majdnem (közel) optimális megoldásra törekszik, mert a valós életben ez az igazán kifizetődő.

Fizikai térben való keresés valódi cselekvéseket igényel, ami valódi veszélyeket is jelenthet, netán katasztrofális kimenetellel, ha ágens döntéseihez hiányos, vagy hibás információt használ (vajon mi történik, ha egy robot hibásan úgy itéli, hogy egy hid el fogja birni a súlyát és útat röviditve megkisérel rajta átkelni?) Gépi ágens, nem fizikai térben keresve a keresési tér matematikai leírásában képes feltérképezni a lehetőségeket, képes büntetlenül visszalépni, rendelkezik végül elegendő számítási kapacitással a nyers erő alkalmazásához. Így akár ideálisan optimális megoldásokra is törekedhet.

Egy ügyes élő ágens azonban (ilyen az ember, de kutya, vagy méhecske már nem tud itt velünk lépést tartani) megtervezhet egy ügyes gépi ágenst, amire a keresési feladatát áthárítja. Ha a keresés absztrakt térben történik, elegendő megtervezni az gépi ágens szoftver belsejét, avagy programját, hiszen minden keresési lépés ágens tudásbázisában történik, az ágens csak „gondolkodik”, a keresés az ágens „fejében” történik. Fizikai térben való keresés esetén a helyzet annál bonyolultabb. Mivel a keresési lépések valóban, az ágenst körül vevő fizikai környezetben történnek, elvégzésükhöz valódi mechanizmusok és erőforrásokat szükségesek. Muszáj ilyenkor megtervezni az ágens fizikai küllemét, azaz architektúráját, aminek központi tervezési kérdése eldönteni, hogy az ágens milyen érzékelő és milyen végrehajtó szervekkel rendelkezzen a siker érdekében. Ha az áthárítás sikerül (képesek vagyunk a keresési tér matematikáját megalkotni, beprogramozni, architektúrát kialakítani, a számításokat kivárni, stb.), akkor majdnem optimális emberi voltunk ellenére is optimális megoldásokhoz juthatunk, amiket majd életbe léptetünk (ilyen pl. az gépkocsi útvonal kereső programok használata). Ilyen megoldásokra tanit minket a könyv.

Meg kell említeni végül, hogy a heurisztikus keresés, mint mechanizmus, központi szerepet foglal Allen Newell és Herbert Simon által javasolt un. fizikai szimbolumrendszer hipotézisben.

Kapcsolódó olvasmányok

fizikai szimbolumrendszer hipotézisről:

Newell, Allen; Simon, H. A. (1976), "Computer Science as Empirical Inquiry: Symbols and Search",Communications of the ACM, March 1976, Vol 19, No 3, pp. 113- 126 (1975 Turing Award Lecture)

(2.54 MB)

http://en.wikipedia.org/wiki/Physical_symbol_system

http://www.rci.rutgers.edu/~cfs/472_html/AI_SEARCH/PhysicalSymbolSystemHyp.html

http://www.rci.rutgers.edu/~cfs/472_html/AI_SEARCH/PSS/PSSH1.html

3.1.4. MEDLINE (Semmelweis Egyetem)

A MEDLINE az amerikai Nemzeti Könyvtár (National Library of Medicine) adatbázisa, amely szakmailag irányadó orvosi információt szolgáltat az orvostudomány, a beteggondozás, a fogászat, az állatorvos-tudomány, az egészséggondozási rendszer, a pre-klinikai tudományok területéről. Az adatbázis a következő oldalon érhető el:

MEDLINE

Az orvostudomány legnagyobb és legtöbbet használt bibliográfiai adatbázisa.

UMLS (Unified Medical Language System)

A MEDLINE adatbázis létrehozása, és használata csak egy egységes orvosi nyelvrendszer kialakításával volt lehetséges

Az egységes orvosi nyelv UMLS kialakítását az NLM kezdte 1986-ban azzal a céllal, hogy olyan rendszerek, kiépítését támogassa, melyek segítségével a szakemberek és kutatók képesek lesznek azoknak az orvos biológiai információknak a visszakeresésére, amelyek különböző forrásokból származnak. Ezzel lehetővé teszik a felhasználók számára, hogy eltérő információs rendszereket, így pl. a számítógépes betegadat feldolgozórendszereket, bibliográfiai és faktografikus adatbázisokat összekapcsoljanak.

Olyan ismeretforrásokat fejlesztett ki, amelyeket a felhasználói programok széles köre tud alkalmazni, leküzdve azokat a nehézségeket, amelyeket a terminológiát érintő különbségek, és az adatbázisokban szétszórtan elhelyezkedő releváns információk miatt a keresést érinti.

A három ismeretforrás:

Metatezaurusz: a betegadat feldolgozás, az egészségügyi adminisztráció, a bibliográfiai és teljes szövegű adatbázisok, a szakértői rendszerek területéről származó orvos biológiai szakszógyűjteményre és osztályozási rendszerre támaszkodva alakított ki egy egységes, integrált formátumot, melynek segítségével összekapcsolja az ugyanarra a fogalomra vonatkozó különféle elnevezéseket. Megőrzi a forrásokból származó eredeti kifejezéseket, jelentéseket, hierarchikus kapcsolatokat, jelzőket és szóközti kapcsolatokat, minden fogalomhoz megadja az alapvető információkat és a különböző szótárakból származó kifejezések között új kapcsolatokat, hoz létre. Segítségével a számítógépes program tolmácsolni tudja a felhasználói kéréseket, interaktív módon finomíttatja a kérdés megfogalmazását, azonosítja a kérdésnek legmegfelelőbb adatbázist és a felhasználó által megadott kifejezést az információs forrás terminológiája szerint fogalmazza át.

A Metatezaurusz a fogalom vagy jelentés köré szerveződik. Az ugyanazt a fogalmat, jelölő neveket (szinonimák, lexikai változatok és fordítások) összekapcsolja.
Szaklexikon: a természetes nyelv használatához biztosítja a lexikai információt. Szintaktikai információkat tartalmaz a kifejezésekről, szóelemekről, angol szavakról, köztük az igékről is, amelyek a Metatezauruszban meg sem találhatók. Minden címszóhoz szintaktikai, morfológiai és helyesírási leírás tartozik.
Szemantikai háló: a Metatezauruszban szereplő fogalmakat kategorizálja 134 szemantikai típusba. A szemantikai típusok között 54 kapcsolat adja meg a Háló szerkezetét, melyek a biomedicina területén a fontos kapcsolatokat jelképezik. Specifikus fogalmakról minden információ a Metatezauruszban keresendő, a Hálóban csak azokról az alapvető szemantikai típusokról találunk információt, amelyeket ezekhez, a fogalmakhoz hozzárendeltek, és azokról a kapcsolatokról, amelyek e szemantikai típusok között létezhetnek. Azokról a kategóriákról ad információt (pl. Betegség vagy szindróma, Vírus), amelyekhez a metatezaurusz összes fogalmát hozzárendelték, valamint a típusok közötti lehetséges kapcsolatokról (pl. a Vírus Betegséget vagy szindrómát eredményezhet).

A keresőmotor az informatikában egy program vagy alkalmazás, amely bizonyos feltételeknek (többnyire egy szónak vagy kifejezésnek) megfelelő információkat keres valamilyen számítógépes környezetben

Az internetes keresőmotorok tipikusan két részből állnak, az egyik összegyűjti az információt, a másik pedig rendszerezi. Az első rész (a szaknyelv robot, spider vagy web crawler néven hivatkozik rá) egyfajta automatizált böngészőprogram, ami a linkeket követve bolyong a weboldalak között, és letölti a tartalmukat. A második rész, az indexelő elemzi a begyűjtött oldalakat, metaadatokat társít hozzájuk, és egy indexet épít, aminek a segítségével a keresési kritériumok alapján könnyen megtalálhatóak a megfelelő oldalak. Amikor a felhasználó elindít egy lekérdezést (tipikusan néhány kulcsszó megadásával), a kereső az index segítségével kiválogatja a kritériumoknak megfelelő oldalakat, a hozzájuk társított metainformációk alapján sorrendbe állítja őket, és a (tipikusan igen nagyszámú) összes találat közül az első néhányat visszaadja a felhasználónak.

Ilyen keresőmotor a MetamorphoSys szoftver.

Alkalmazásával egyénre szabott metatezauruszok hozhatók létre, segítségével pl. ki lehet zárni az adott felhasználó számára nyelvileg érdektelen szókészleteket vagy a felhasználóra szabott szókészletet lehet beállítani.

MeSH

A MeSH (Medical Subject Headings - orvosi tárgyszórendszer) a következő oldalon található:

MeSH

Segítségével mintegy 5 000, túlnyomórészt angol nyelvű indexelt folyóiratban kereshetünk (1950-ig visszamenően). Az adatbázist ma már több szolgáltatótól, és felhasználói felületről elérhetjük. Bibliográfiai adatok találhatók a következő forrásokból: Index Medicus, International Nursing Index, Index to Dental Literature, PREMEDLINE®, AIDSLINE®, BIOETHICSLINE®, HealthSTAR.

A MeSH az orvosi szakirodalomban és határterületein az információ feldolgozás és visszakeresés nemzetközi mércéjévé vált. A MeSH tezaurusz segítségével az amerikai Országos Orvostudományi Könyvtár, az NLM (National Library of Medicine) a vezető orvosi folyóiratot indexel a Medline számára, de egyéb dokumentumok (könyvek, audiovizuális anyagok) feldolgozására is ezt a tárgyszórendszert alkalmazzák. Egy bibliográfiai tételhez egyszerre több, a tartalmat részletesen feltáró MeSH kifejezés tartozik. A visszakeresés ugyancsak a MeSH segítségével történik.

A MeSH magyarítását a Medinfo kezdte el és megalkotta a HunMeSH-t. A Magyar Orvosi Bibliográfia már ezen az elven működik.

HunMeSH

A HunMeSH az egységes orvosi nyelv rendszerének (UMLS) alapján a magyar orvosi tezaurusz tökéletesítése és kiegészítése a szakterületek terminológiájával, egy korszerű, magyar nyelven a szakirodalmi tájékoztatási eszköz eléréséhez, létrehozva ezzel egy olyan szógyűjteményt, amely magyarul adja meg a magyar orvosi szakkifejezések magyarázatát, és közli a szó angol és latin megfelelőjét.

A HunMeSH-nek tartalmaznia kell a deszkriptorokat, az utalásokat és szinonimákat. A HunMeSH az UMLS szerkezetét kell, hogy kövesse. A végső cél az, hogy kötött kereső szótárak, tezauruszok támogatásával a természetes nyelven alapuló keresés segítségével könnyítsük meg a felhasználó dolgát.

A tezauruszban található összes tárgyszó vagy deszkriptor az online kereséshez is felhasználható, és szinte mindegyik egyaránt alkalmas az indexelésre és katalogizálásra. Az indexelés során a feldolgozó annyi deszkriptort rendel egy dokumentumhoz, amennyivel annak tartalmát a lehető legpontosabban tudja feltárni. A 10-12 tárgyszóból csillaggal jelzik az online változatban azokat, amelyek a legfontosabb információt jelentik a cikkel kapcsolatosan. A többi deszkriptor azokat a fogalmakat jelöli, amelyeket a cikk érintőlegesen tárgyal. Vannak olyan speciális kifejezések (kvalifikátorok) is, amelyeket az Index Medicus nem használ (így csillag sem kerül soha eléjük), az indexelés és online keresés során viszont nagyon hasznosak. Ilyen kvalifikátornak számít a kiadvány típusa, az ellenőrző cédula (TG) és a földrajzi név.

A MeSH kötött tárgyszó-rendszer, tezaurusz. A tezaurusz szakkifejezések olyan gondosan szerkesztett és ellenőrzött tárházát jelenti, ahol ezek a kifejezések egymással alá, fölé vagy mellérendelt viszonyban állnak. Így jön létre az a hierarchikus (fa) szerkezet, melynek segítségével a keresést különböző szinteken (a keresést szűkítve vagy tágítva) végezhetjük. A tezaurusz funkciója, hogy felsorolja és meghatározza a szótár megengedett és érvénytelen elemeit, és megmutassa, milyen kapcsolat van az érvényes elemek között.

A szakkifejezések és tárgyszavak abc sorrendben és hierarchikus felépítésükben is visszakereshetők. A hierarchikus szerkezet legáltalánosabb szintjén találjuk a legáltalánosabb tárgyszavakat (deszkriptorokat), mint pl. IDEGRENDSZER. Alatta a KÖZPONTI IDEGRENDSZER, ennél alacsonyabb szinten az ennél specifikusabb tárgyszavakat, mint pl. AGY, innen az AGYTÖRZS, és így tovább.

Főtárgyszavak (deszkriptorok) száma és több ezerre az utalószavak (nemdeszkriptorok) száma, melyek segítenek a megfelelő tárgyszó megkeresésében, pl. B₆- vitamin ld. Piridoxin. A szinonimák, rövidítések, eltérő írásmódok beillesztésével, az utaló rendszer kidolgozásával a felhasználó könnyebben jut el a MeSH-hez.

Altárgyszavak: ezek segítségével a főtárgyszó által jelzett fogalmat csak bizonyos szempont(ok)ból vizsgáljuk. Így például a MÁJBETEGSÉGEK-diagnózis kombináció azt jelzi az indexelő-katalogizáló, visszakereső számára, hogy a cikk nem általában a májbetegségekről szól, hanem annak diagnózisáról. Egy főtárgyszóhoz több altárgyszó is tartozhat, ezek abc sorrendben kerülnek felsorolásra. Egy főtárgyszóhoz nem szükségszerűen ugyanazok az altárgyszavak tartoznak.

Faszerkezet: a deszkriptor helyét mutatja más deszkriptorok viszonylatában egy témakörön belül. Pl: az egyes speciális agyi idegek esetében azt látjuk, hogy egy tágabb deszkriptornak, az AGYI IDEGEK-nek vannak alárendelve. Minden deszkriptornak van legalább egy ilyen besorolása, melynek segítségével általánosabbá, szélesebbé tehetjük a keresést, vagy éppenséggel specifikusabb területeket választhatunk.