15.2. Következtetés időbeli modellekben
Egy általános időbeli modellstruktúra kidolgozása után, most már megfogalmazhatjuk a megoldandó alapvető következtetési feladatokat:
-
Szűrés (filtering) vagy ellenőrző megfigyelés (monitoring). Ez a bizonyossági állapot (belief state) kiszámításának a feladata – ami a jelenlegi állapot feletti a posteriori eloszlás, az adott időpontig vett összes bizonyíték ismeretében. Azaz szeretnénk kiszámítani a P(Xt|e1:t) mennyiséget, feltéve, hogy a bizonyítékok folyamatos sorozatban érkeznek kezdve a t = 1 időponttól. Az esernyős példában ez az aznapi eső valószínűségének a kiszámítását jelentené, az esernyőhordozó eddigi összes megfigyelésének az ismeretében. A szűrés az, amit egy racionális ágensnek el kell végeznie ahhoz, hogy a jelenlegi állapotot követni tudja, és így racionális döntéseket hozhasson (lásd 17. fejezet). Kiderül, hogy majdnem azonos számítás szolgáltatja a bizonyítéksorozat megfigyelésének a valószínűségét (likelihood), P(e1:t)-t.
-
Előrejelzés (prediction). Ez egy jövőbeli állapot feletti a posteriori eloszlás kiszámításának a feladata, az adott időpontig vett összes bizonyíték ismeretében. Azaz, szeretnénk kiszámítani a P(Xt+k|e1:t) mennyiséget valamely k > 0 esetén. Az esernyős példában ez jelentheti az eső valószínűségének a kiszámítását három napra előre, az esernyőhordozó eddigi összes megfigyelésének az ismeretében. Az előrejelzés hasznos a cselekedetek lehetséges sorozatainak a kiértékelésében.
-
Simítás (smoothing) vagy visszatekintés (hindsight). Ez egy múltbeli állapot feletti a posteriori eloszlás kiszámításának a feladata, a jelen időpontig vett összes bizonyíték ismeretében. Azaz szeretnénk kiszámítani a P(Xk|e1:t) mennyiséget valamely 0 ≤ k < t esetén. Az esernyős példában ez jelentheti az eső valószínűségének a kiszámítását múlt szerdára, ha ismerjük az esernyőhordozónak a mai napig történő összes megfigyelését. A visszatekintés az állapotnak egy jobb becslését adja, mint ami akkor elérhető volt, mivel több bizonyítékot használ fel.
-
Legvalószínűbb magyarázat (most likely explanation). A megfigyelések egy sorozatának ismeretében lehet, hogy szeretnénk megtalálni azt az állapotsorozatot, ami a leginkább valószínű, hogy az adott megfigyeléseket generálta. Azaz szeretnénk kiszámítani az
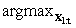 P(x1:t|e1:t) értékét. Például ha az esernyő feltűnik az első három nap mindegyikén, és hiányzik a negyediken, akkor a legvalószínűbb magyarázat az, hogy az első három napon esett és a negyediken nem esett. Az erre a feladatra szolgáló algoritmusok számos alkalmazásban hasznosak, ideértve a beszédfelismerést – ahol a cél a szavak legvalószínűbb sorozatának a megtalálása hangok sorozatának ismeretében – és egy zajos csatornán továbbított bináris szekvenciák rekonstrukcióját.
P(x1:t|e1:t) értékét. Például ha az esernyő feltűnik az első három nap mindegyikén, és hiányzik a negyediken, akkor a legvalószínűbb magyarázat az, hogy az első három napon esett és a negyediken nem esett. Az erre a feladatra szolgáló algoritmusok számos alkalmazásban hasznosak, ideértve a beszédfelismerést – ahol a cél a szavak legvalószínűbb sorozatának a megtalálása hangok sorozatának ismeretében – és egy zajos csatornán továbbított bináris szekvenciák rekonstrukcióját.
Ezeken a feladatokon túl szükség van még módszerekre az állapotátmenet- és érzékelő modellek megfigyelésekből történő megtanulására. Csakúgy, mint a statikus Bayes-hálóknál, a dinamikus Bayes-hálós tanulás elvégezhető mint a következtetés mellékterméke. A következtetés egy becslést ad arra, hogy milyen átmenetek következtek be valójában, és milyen állapotok generálták az érzékelők értékeit, és ezek a becslések felhasználhatók a modell frissítésére. A frissített modellek jobb becsléseket adnak, és a folyamat a konvergálásig iterálódik. A teljes folyamat a várhatóérték-maximálás vagy EM algoritmus egy esete (lásd 20.3. alfejezet). Figyelemre méltó részlet, hogy a tanulás teljes simítós következtetést igényel szűrés helyett, mivel ez jobb becsléseket ad a folyamat állapotára. Lehet, hogy a szűréssel való tanulás nem konvergál helyesen; gondoljunk például a gyilkosságok felderítésének a megtanulására: a visszatekintés mindig szükséges annak kikövetkeztetéséhez a megfigyelhető bizonyítékok alapján, hogy mi történt a gyilkosság helyszínén.
Az előző szakaszban felsorolt négy következtetési feladatot megoldó algoritmusok először leírhatók általános szinten, függetlenül az alkalmazott modell konkrét típusától. Az egyes modellekhez igazodó javításokat a következő fejezetekben ismertetjük.
Kezdjük a szűréssel. Megmutatjuk, hogy ez menet közben egyszerűen, online módon elvégezhető: a t-edik időpillanatig tartó szűrés eredményét ismerve, a t + 1-edik időpillanatra az eredmény könnyen kiszámítható az új et+1 bizonyítékból. Azaz
P(Xt+1|e1:t+1) = f(et+1, P(Xt|e1:t))
valamely f függvénnyel. Ezt a folyamatot gyakran nevezik rekurzív becslésnek (recursive estimation). Tekinthetjük a számítást úgy, mint ami valójában két részből áll: elsőként a jelenlegi állapot eloszlását terjesztjük előre t-ről t + 1-re; azután fogjuk frissíteni, felhasználva az új et+1 bizonyítékot. Ez a kétlépéses folyamat elég egyszerűen alakul:
P(Xt+1|e1:t+1) = P(Xt+1|e1:t, et+1) (felosztva a bizonyítékot)
= α P(et+1|Xt+1, e1:t) P(Xt+1|e1:t) (a Bayes-szabályt használva)
= α P(et+1|Xt+1) P(Xt+1|e1:t) (a bizonyíték Markov-tulajdonsága miatt)
Itt és végig a fejezetben, az α egy normalizációs konstans, ami a valószínűségek 1-re összegzését biztosítja. A második tényező P(Xt+1|e1:t) reprezentálja a következő állapot egylépéses előrejelzését, és az első tényező ezt frissíti az új bizonyítékkal. Vegyük észre, hogy P(et+1|Xt+1) közvetlenül kinyerhető az érzékelő modellből. Most a jelenlegi Xt állapotot feltételnek véve a következő állapot egylépéses előrejelzéséhez jutunk:
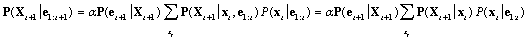 (kihasználva a Markov-tulajdonságot)(15.3)
(kihasználva a Markov-tulajdonságot)(15.3)
Az összegzésen belül az első tényező egyszerűen az állapotátmenet-modell és a második a jelenlegi állapot eloszlása. Így megvan a kívánt rekurzív képlet. A szűrt P(Xt|e1:t) becslésre úgy gondolhatunk, mint egy f1:t „üzenetre”, amit előre terjesztünk végig a sorozaton, minden átmenetnél az új megfigyeléssel módosítva és frissítve. A folyamat
f1:t+1 = α Előre(f1:t, et+1)
ahol az ELŐRE a (15.3) egyenlet által leírt frissítést hajtja végre.
Fontos
Ha az összes állapotváltozó diszkrét, minden frissítés ideje állandó (azaz t-től független), és a tárigény is állandó. (Ezek az állandók természetesen függnek az állapottér méretétől és a tárgyalt időbeli modell konkrét típusától.) A frissítés idő- és tárigényének állandónak kell lennie, ha egy korlátos memóriájú ágensnek követnie kell az aktuális állapot eloszlását a megfigyelések egy korlátlan sorozata esetén.
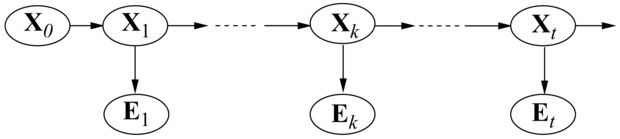
Mutassuk be a szűrési folyamatot két lépésen keresztül az alap esernyős példában (lásd 15.2. ábra). Feltesszük, hogy a biztonsági őrünknek van valamilyen a priori hite, hogy a 0. napon esett-e, éppen azelőtt, hogy a megfigyelések sorozata elkezdődik. Tegyük fel, hogy ez P(R0) = 〈0,5, 0,5 〉. Most a két megfigyelést a következőképpen dolgozzuk fel:
-
Az 1. napon az esernyő feltűnik, így U1 = igaz. Az előrejelzés t = 0-ról t = 1-re
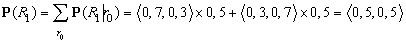
és a t = 1-beli bizonyítékkal való frissítés azt adja, hogy
P(R1|u1) = αP(u1|R1) P(R1) = α〈0,9, 0,2〉〈0,5, 0,5〉
= α〈0,45, 0,1〉 ≈ 〈0,818, 0,182〉
-
A 2. napon az esernyő feltűnik, így U2 = igaz. Az előrejelzés t = 1-ről t = 2-re
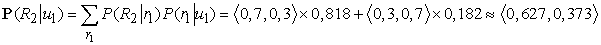
a t = 2-beli bizonyítékkal való frissítés pedig azt adja, hogy
P(R2|u1, u2) = αP(u2|R2) P(R2|u1) = α〈0,9, 0,2〉 〈0,627, 0,373〉
= α〈0,565, 0,075〉 ≈ 〈0,883, 0,117〉
Érzésünk szerint az eső valószínűsége azért növekedett az 1. napról a 2. napra, mert az eső folytatódik. A 15.2. (a) feladat ennek a tendenciának a további vizsgálatát kéri.
Az előrejelzés feladatát tekinthetjük egyszerűen szűrésnek új bizonyíték hozzáadása nélkül. Valójában a szűrési folyamat már magában foglal egy egylépéses előrejelzést és könnyen származtatható a következő rekurzív számítás a t + k + 1 állapot előrejelzésére a t + k előrejelzéséből:
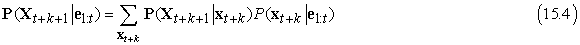
Természetesen ez a számítás csak az állapotátmenet-modellt tartalmazza és nem az érzékelő modellt.
Érdekes meggondolni, hogy mi történik, ahogy egyre távolabbra próbálunk előre jelezni a jövőben. A 15.2. (b) feladat megmutatja, hogy az eső előrejelzett eloszlása a 〈0,5, 0,5〉 fix ponthoz konvergál, ami után a továbbiakban állandó marad. Ez az állapotátmenet-modell által meghatározott Markov-folyamat stacionárius eloszlása (stationary distribution) (lásd még 14.5.2. szakasz - Következtetés Markov-lánc szimulációval rész). Rengeteg ismeret gyűlt fel az ilyen eloszlások tulajdonságairól és a keverési időről (mixing time) – ami nagyjából a fix pont eléréséig eltelt idő. Gyakorlati szempontból ez bukásra ítél minden olyan kísérletet, ami a keverési idő kis hányadánál nagyobb számú lépés múlva kísérli meg az aktuális állapot előrejelzését. Minél bizonytalanabb az állapotátmenet-modell, annál rövidebb a keverési idő, és a jövő annál homályosabb.
A szűrésen és az előrejelzésen túl, felhasználhatjuk az előrehaladó rekurziót egy bizonyítéksorozat P(e1:t) valószínűségének a kiszámítására is. Ez egy hasznos mennyiség, ha különböző időbeli modelleket szeretnénk összehasonlítani, amelyek ugyanazt a bizonyítéksorozatot állíthatták elő; például a 15.6. alfejezetben különböző szavakat hasonlítunk össze, amelyek ugyanazt a hangsort állíthatták elő. Ehhez a rekurzióhoz felhasználjuk az ℓ1:t = P(Xt, e1:t) valószínűségi (likelihood) üzenetet. Egyszerű feladat azt megmutatni, hogy
ℓ1:t+1 = Előre(ℓ1:t, et+1)
Kiszámítva ℓ 1:t-t, az aktuális valószínűséget az Xt feletti összegzéssel kapjuk:

Ahogy korábban meghatároztuk, a simítás (smoothing) múltbeli állapotok feletti eloszlás kiszámításának a folyamata a jelenig tartó bizonyítékok ismeretében; azaz P(Xk|e1:t) számítása valamely 0 ≤ k < t esetén (lásd 15.3. ábra). Ez legkényelmesebben két részletben végezhető el – a bizonyíték k-ig és a bizonyíték k + 1-től t-ig,
P(Xk|e1:t) = P(Xk|e1:k, ek+1:t)
= α P(Xk|e1:k) P(ek+1:t|Xk, e1:k) (a Bayes-szabályt használva)
= α P(Xk|e1:k) P(ek+1:t|Xk) (a feltételes függetlenséget használva)
= α f1:k bk+1:t (15.6)
ahol definiáltuk a bk+1:t = P(ek+1:t|Xk) „visszafelé” üzenetet, analóg módon az f1:k előre üzenethez. Az f1:k előre üzenetet előre szűréssel lehet kiszámolni 1-től k-ig, a (15.3) egyenlet alapján. A bk+1:t visszafelé üzenetről pedig kiderül, hogy egy egyszerű rekurzív folyamattal kiszámítható, ami t-től visszafelé halad:
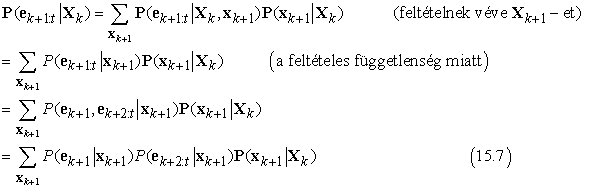
ahol az utolsó lépés az ek+1 és az ek+2:t feltételes függetlenségéből következik az xk+1 melletti feltétellel. Az összegzésben a három tényezőből az első és a harmadik közvetlenül a modellből megkapható, a második pedig a „rekurzív hívás”. Az üzenetjelölést használva kapjuk, hogy
bk+1:t = Hátra(bk+2:t, ek+1:t)
ahol a HÁTRA a (15.7) egyenlet által leírt frissítést hajtja végre. Ahogy az előrefelé rekurziónál, az egyes frissítésekhez szükséges idő- és tárigény állandó, és így t-től független itt is.
Most láthatjuk, hogy a (15.6) egyenlet mindkét tényezője kiszámítható időbeli rekurzióval, az egyik előrefelé fut 1-től k-ig, és a szűrés (15.3) egyenletét használja, a másik visszafelé fut t-től k+1-ig, és a (15.7) egyenletet használja. Figyeljünk arra, hogy a viszszafelé fázist bt+1:t = P(et+1:t|Xt) = 1-gyel inicializáljuk, ahol 1 egy egyesekből álló vektor. (Mivel et+1:t egy üres sorozat, a megfigyelésének valószínűsége 1.)
Alkalmazzuk most ezt az algoritmust az esernyős példára, kiszámítva az eső valószínűségének simított becslését t = 1-nél, az első és második nap megfigyeléseinek ismeretében. A (15.6) egyenlet szerint ezt az adja meg, hogy
P(R1|u1, u2) = α P(R1|u1) P(u2|R1) (15.8)
A korábban leírt előrefelé szűrési folyamatból már tudjuk, hogy az első tényező 〈0,818, 0,182〉. A második tényezőt a (15.7) egyenletbeli visszafelé rekurziót alkalmazva számíthatjuk ki:
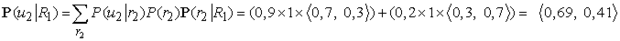
Ezt visszahelyettesítve a (15.8) egyenletbe azt kapjuk, hogy a simított becslés az esőre az 1. napon
P(R1|u1, u2) = α 〈0,818, 0,182〉 × 〈0,69, 0,41〉 ≈ 〈0,883, 0,117〉
Így ebben az esetben a simított becslés nagyobb, mint a szűrt becslés (0,818). Ennek oka az, hogy az esernyő a 2. napon valószínűbbé teszi, hogy esett a 2. napon, és mivel az eső tartósan szokott esni, ez még valószínűbbé teszi, hogy esett az 1. napon.
Mind az előrefelé, mind a visszafelé haladó rekurzió lépésenként állandó időt igényel; így a simítás időkomplexitása e1:t bizonyíték esetén O(t). Ez egy konkrét k időlépésbeli simítás komplexitása. Ha a teljes szekvenciát szeretnénk simítani, nyilvánvaló módszer, hogy egyszerűen az egész simítási folyamatot lefuttatjuk minden egyes simítandó időpillanatra. Ez O(t2) időkomplexitást eredményez. Jobb megközelítés a dinamikai programozás nagyon egyszerű alkalmazásával O(t)-re csökkenti a komplexitást. A megoldás kulcsa megjelent az esernyős példa előző elemzésében, ahol az előrefelé szűrés folyamatának eredményeit újra fel tudtuk használni. A lineáris idejű algoritmus kulcsa így az előrefelé szűrés eredményeinek a tárolása az egész sorozatnál. Aztán a visszafelé rekurziót futtatjuk t-től 1-ig, kiszámítva a szűrt becslést minden k lépésnél a kiszámolt bk+1:t visszafelé üzenetből és a tárolt f1:k előrefelé üzenetből. Az algoritmus, amit találóan előre-hátra algoritmusnak (forward-backward algorithm) neveznek, a 15.4. ábrán látható.
ELŐRE és a HÁTRA műveleteket rendre a (15.3) és (15.7) egyenletek definiálják.
A figyelmes olvasó észrevehette, hogy a 15.3. ábrán látható Bayes-hálóstruktúra egy polifa (polytree) a 14. fejezet szóhasználatában. Ez azt jelenti, hogy a csoportosító algoritmus egy nyilvánvaló alkalmazása szintén lineáris idejű algoritmust eredményez, ami a teljes sorozatra kiszámítja a simított becslést. Mára már világossá vált, hogy az előre-hátra algoritmus valójában a csoportosító eljárásokban használt polifa terjesztési algoritmusnak egy speciális esete (bár a kettőt egymástól függetlenül fejlesztették ki).
Az előre-hátra algoritmus alkotja a gerincét azon számítási módszereknek, amelyeket számos zajos megfigyelések sorozatával foglalkozó alkalmazásban használnak, a beszédfelismeréstől a repülőgépek radarkövetéséig. Ahogy leírtuk, két gyakorlati hátránya van. Az első, hogy a tárigénye túl nagy lehet azoknál az alkalmazásoknál, ahol az állapottér nagy, és a sorozatok hosszúak, mivel O(|f|t) méretű tárat használ, ahol |f| az előrefelé üzenet reprezentációjának a mérete. A tárigény O(|f|log t)-re csökkenthető az időkomplexitásnak egy log t tényezővel történő egyidejű megnövelése árán, ahogy a 15.3. feladat mutatja. Bizonyos esetekben (lásd 15.3. alfejezet) egy állandó tárigényű algoritmus használható időbüntetés nélkül.
Az alapalgoritmus második hátránya, hogy a folyamatos (online) működéshez módosítást igényel. Ekkor ugyanis a korábbi időpontokhoz simított becsléseket kell kiszámítanunk, amint folyamatosan új megfigyelések érkeznek a sorozat végéhez. A leggyakoribb követelmény az állandó időkülönbségű simítás (fixed-lag smoothing), ami a P(Xt–d|e1:t) simított becslés kiszámítását jelenti egy rögzített d-re. Azaz a simítást a jelenlegi t időpillanat előtt d lépéssel lévő időpontra végezzük el; t növekedését a simításnak is követnie kell. Nyilvánvaló, hogy lefuttathatjuk az előre-hátra algoritmust a d lépéses „ablakban”, amint egy új bizonyíték adódik, de ez nem tűnik hatékonynak. A 15.3. alfejezetben látni fogjuk, hogy az állandó időkülönbségű simításnál egy frissítés bizonyos esetekben állandó idő alatt megtehető, függetlenül a d időkülönbségtől.
Tegyük fel, hogy a biztonsági őr esernyősorozata a munkája első öt napjában az [igaz, igaz, hamis, igaz, igaz]. Mi a legvalószínűbb időjárás-sorozat, ami ezt megmagyarázza? Az esernyő hiánya a 3. napon azt jelenti, hogy nem esett, vagy azt, hogy az igazgató elfelejtette elhozni? Ha a 3. napon nem esett, talán a 4. napon sem esik (mivel az időjárás nem változik gyorsan), de ekkor az igazgató puszta óvatosságból hozta az esernyőt. Összességében 25 lehetséges időjárás-sorozatot választhatunk. Létezik-e módszer a legvalószínűbb sorozat megkeresésére, az összes felsorolása nélkül?
Az egyik megközelítés, amit kipróbálhatunk a következő lineáris idejű algoritmus: használjuk a simító algoritmust, hogy megtaláljuk az időjárás a posteriori eloszlását minden időpillanatban; majd állítsuk elő a sorozatot minden egyes lépésnél az a posteriori szerinti legvalószínűbb időjárást felhasználva. Egy ilyen megközelítést kötelező gyanakvással kell fogadnia az olvasónak, mivel a szűrés által kiszámított a posteriori eloszlások az egyes időpontok feletti eloszlások, ezzel szemben a legvalószínűbb sorozat megtalálásához az összes időpont feletti együttes valószínűségeket kell figyelembe venni. Az eredmények valójában nagyon különbözők lehetnek (lásd 15.4. feladat).
Lineáris idejű algoritmus azonban létezik a legvalószínűbb sorozat megtalálására, de kicsit több gondolkozást igényel. Ugyanazon a Markov-tulajdonságon alapul, mint ami hatékony algoritmusokat eredményezett a szűrésre és a simításra. A problémáról való gondolkodás legkönnyebb módja, hogy ha minden sorozatot egy útvonalnak tekintünk egy gráfban, aminek a csomópontjai az egyes időpillanatokban a lehetséges állapotok. Egy ilyen gráf látható az esernyős problémára a 15.5. (a) ábrán. Most gondoljuk meg a gráfon keresztül vezető legvalószínűbb út megkeresésének a problémáját, ahol egy út valószínűsége (a likelihood érték) az útvonal menti átmenetek valószínűségeinek és az egyes állapotokban adott megfigyelések valószínűségeinek a szorzata. Koncentráljunk most azokra az útvonalakra, amelyek elérik az Eső5 = igaz állapotot. A Markov-tulajdonság miatt fennáll, hogy az Eső5 = igaz állapotba vezető legvalószínűbb útvonal tartalmazza azt a legvalószínűbb útvonalat, amely valamelyik 4. időpontbeli állapotba vezet, és amit egy átmenet követ az Eső5 = igaz-ba; a 4. időpontbeli állapot pedig, ami része lesz az Eső5 = igaz-ba vezető útnak, az az állapot, amelyik maximalizálja ennek az útvonalnak a valószínűségét.
Fontos
Másképpen fogalmazva, van egy rekurzív kapcsolat az xt+1 állapotokba vezető legvalószínűbb útvonalak és az xt állapotokba vezető legvalószínűbb útvonalak között. Ez a kapcsolat olyan egyenletként írható fel, amely az útvonalak valószínűségeit kapcsolja össze:
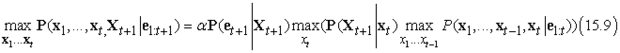
A (15.9) egyenlet megegyezik a szűrés (15.3) egyenletével, azzal a kivétellel, hogy
-
az f1:t= P(Xte1:t) előre üzenet helyett a következő üzenet szerepel:
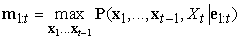
ami az xt állapotba vezető legvalószínűbb út valószínűségeit adja meg; és
-
a (15.3) egyenletbeli xt feletti összegzés helyett a (15.9) egyenletben az xt feletti maximalizálás szerepel.
Így a legvalószínűbb állapotsorozat kiszámítása hasonló a szűréshez: előrefelé végigfut a sorozaton, minden időpontban kiszámítva az m üzeneteket a (15.9) egyenlet szerint. A számítás menetét a 15.5. (b) ábra mutatja. Végül ez kiadja az összes végső állapothoz vezető legvalószínűbb útvonal valószínűségét. Így már könnyen kiválasztható a teljes hosszúságú legvalószínűbb sorozat (a vastagon szedettel kiemelt végső állapottól). Az aktuális sorozat azonosításához – szemben azzal, amikor csak a valószínűségét számítjuk ki – az algoritmusnak minden állapotból mutatókat kell nyilvántartania a legjobb hozzá vezető állapothoz (vastagon szedettel látható); a sorozat a mutatóknak a legjobb végső állapottól való visszafelé követésével határozható meg.
![(a) Az Esőt lehetséges állapotsorozatait tekinthetjük egy átvezető útnak egy gráfon, aminek csomópontjai a lehetséges állapotok az egyes időpontokban. (Az állapotokat négyzetes csomópont jelzi, hogy félreérthetetlenül megkülönböztessük őket egy Bayes-háló csomópontjaitól.) (b) A Viterbi-algoritmus működése az [igaz, igaz, hamis, igaz, igaz] megfigyelési sorozatra. Minden t időpontra feltüntettük az m1:t üzenet értékeit, ami minden egyes t időpontbeli állapothoz megadja a legjobb, benne végződő sorozat valószínűségét. Minden egyes állapothoz egy vastag nyíl is vezet, ami a legjobb elődjét jelzi, a megelőző sorozat valószínűségének és az átmenet valószínűségének a szorzata szerint. A vastag nyilak visszafelé követése az m1:5-beni legvalószínűbb állapotból pedig megadja a legvalószínűbb sorozatot.](/mi_almanach/sites/default/files/books/35/files/kepek/15-05.png)
Az előzőleg leírt algoritmust Viterbi-algoritmusnak nevezik a megalkotója után. Hasonlóan a szűrési algoritmushoz, ennek a komplexitása is lineáris t-ben, a sorozat hosszában. Azonban eltérően a szűréstől, a tárigénye szintén lineáris t-ben. Ez azért van így, mert a Viterbi-algoritmusban mutatókkal kell nyilvántartani az egyes állapotokhoz vezető legjobb sorozatot.

