Az alapelem minden mintavételi algoritmusban a minták generálása egy ismert valószínűség-eloszlásból. Például egy szabályos érme felfogható egy Érme valószínűségi változónak 〈fej,írás〉 értékekkel és P(Érme) = 〈0,5, 0,5〉 a priori eloszlással. A mintavétel ebből az eloszlásból pontosan megfelel egy érme dobálásának: 0,5 valószínűséggel fej-et ad, és 0,5 valószínűséggel írás-t. Ha rendelkezésre áll a [0, 1] tartományba eső véletlen számoknak egy forrása, akkor bármely egyváltozós eloszlásból egyszerű dolog mintavételezni (lásd 14.9. feladat).

A véletlen mintavételezési folyamat legegyszerűbb fajtája Bayes-hálók esetén a hálóból generál olyan eseményeket, amelyekhez nem kapcsolódik bizonyíték. Az ötlet az, hogy mintavételezzünk minden változót egymás után, topológiai sorrendben. A valószínűség-eloszlás, amiből az értéket mintavételezzük, feltételesen függ a változó szüleihez már hozzárendelt értékektől. Ez az algoritmus látható a 14.12. ábrán. A működését a 14.11. (a) ábrán látható hálón szemléltetjük, feltételezve egy [Felhős, Locsoló, Eső, VizesPázsit] sorrendezést:

Ebben az esetben a PRIOR-MINTA a következő eseményt adja [igaz, hamis, igaz, igaz].

Könnyen látható, hogy a PRIOR-MINTA a háló által meghatározott a priori együttes eloszlásból generál mintákat. Először, legyen S_PS(x₁, …, x_n) annak a valószínűsége, hogy egy adott eseményt legenerál a PRIOR-MINTA algoritmus. Pusztán a mintavételi folyamat alapján felírható, hogy

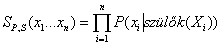
mivel minden mintavételi lépés a szülő értékektől függ.

Ez a kifejezés ismerős, mivel – ahogy ezt a (14.1) egyenlet kimondja – ez egyben a valószínűsége is az együttes eloszlás Bayes-hálós reprezentációja szerinti eseménynek is. Arra jutottunk tehát, hogy

SPS(x1…xn) = P(x1…xn)

Ez az egyszerű tény nagyon könnyűvé teszi lekérdezések – minták felhasználásával történő – megválaszolását.

Bármilyen mintavételi algoritmusban a válasz kiszámítása a generálás során előálló minták megszámlálása alapján történik. Tételezzük fel, hogy N teljes mintánk van, és jelölje N(x₁, …, x_n) az x₁, …, x_n esemény gyakoriságát. Azt várjuk, hogy ez a gyakoriság határértékben konvergáljon a várható értékéhez a mintavételi valószínűség szerint:

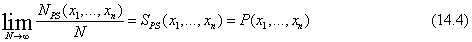
Például gondoljuk meg az előbb generált eseményt: [igaz, hamis, igaz, igaz]. Ennek az eseménynek a mintavételi valószínűsége:

SPS(igaz, hamis, igaz, igaz) = 0,5 × 0,9 × 0,8 × 0,9 = 0,324

Így, N nagy értékeinél azt várjuk, hogy a minták 32,4%-a ez az esemény legyen.

A következőkben, amikor a közelítő egyenlőség jelet („≈”) használjuk, pontosan ilyen értelemben használjuk – azaz a becsült valószínűség egzakttá válik a nagy mintaszámú határesetben. Az ilyen becsléseket konzisztensnek (consistent) nevezzük. Például bármely részlegesen meghatározott x₁, …, x_m esemény valószínűségének egy konzisztens becslése a következőképpen kapható meg, ha m ≤ n:

P(x1,…, xm) ≈ NPS(x1,…, xm)/N (14.5)

Azaz, az esemény valószínűsége megbecsülhető a mintavételi folyamat által generált összes teljes esemény azon hányadával, amelyek illeszkednek a részlegesen meghatározott eseményre. Például ha generálunk 1000 mintát a locsolós hálóból, és 511-ben közülük az Eső = igaz, akkor az eső becsült valószínűsége .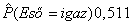

Elutasító mintavételezés Bayes-hálókban

Az elutasító mintavételezés (rejection sampling) általános módszer minták előállítására egy nehezen mintavételezhető eloszlásból, felhasználva egy könnyen mintavételezhető eloszlást. Legegyszerűbb formájában feltételes valószínűségek kiszámítására – azaz P(X∣e) meghatározására használható fel. Az ELUTASÍTÓ-MINTAVÉTELEZÉS algoritmusa a 14.13. ábrán látható. Először a háló által megadott a priori eloszlásból generál mintákat, majd elutasítja azokat, amelyek nem illeszkednek a bizonyítékhoz. Végül, a 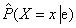becslés megkapható az X = x előfordulásainak megszámlálásával a megmaradt mintában.

Legyen 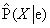az algoritmus által kiadott becsült eloszlás. Az algoritmus definíciója szerint fennáll, hogy

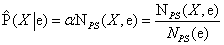
A 14.5 egyenletből kapjuk, hogy

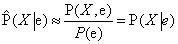
Azaz az elutasító mintavétel az igazi valószínűség konzisztens becslését adja.

Folytatva a 14.11. (a) ábra szerinti példánkat, tételezzük fel, hogy meg szeretnénk becsülni a P(Eső∣Locsoló = igaz)-t, 100 minta felhasználásával. A 100 általunk generált mintából, tegyük fel, hogy 73-ban teljesül, hogy Locsoló = hamis, és így elutasított, míg 27-ben fennáll, hogy Locsoló = igaz; a 27-ből 8-ban Eső = igaz, 19-ben pedig Eső = hamis. Így a

P(Eső∣Locsoló = igaz) ≈ Normalizál(〈8, 19〉) = 〈0,296, 0,704〉

A helyes érték 〈0,3, 0,7〉. A begyűjtött minták szaporodásával a becslés konvergálni fog a helyes értékhez. A becslés szórása az egyes valószínűségeknél arányos lesz 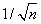-nel, ahol n a becsléshez felhasznált minták száma.

Az elutasító mintavétel legnagyobb hibája, hogy nagyon sok mintát utasít el! Az e bizonyítékkal konzisztens minták aránya exponenciálisan egyre kevesebb, ahogy a bizonyítékváltozók száma nő, így az eljárás egyszerűen használhatatlan komplex problémákban.

Vegyük észre, hogy az elutasító mintavétel nagyon hasonló a feltételes valószínűségek becsléséhez, ha közvetlenül a valódi világból történik a becslés. Például a P(Eső∣VörösAzÉgEste = igaz) becslésénél egyszerűen megszámoljuk, milyen gyakran esik az után, hogy az előző este az ég vörös volt – figyelmen kívül hagyva azokat az estéket, amikor az ég nem volt vörös. (Itt a világ maga játssza a mintageneráló algoritmus szerepét.) Nyilvánvalóan, ha az ég nagyon ritkán vörös, akkor ez hosszú időt vehet igénybe, és ez az, ami az elutasító mintavétel gyengesége.

Valószínűségi súlyozás

A valószínűségi súlyozás (likelihood weighting) elkerüli az elutasító mintavételezés gyengeségét azáltal, hogy csak az e bizonyítékkal konzisztens eseményeket generál. Az algoritmus működésének a leírásával kezdjük; majd megmutatjuk, hogy helyesen működik – azaz, hogy konzisztens valószínűség becsléseket generál. A VALÓSZÍNŰSÉGI-SÚLYOZÁS (lásd 14.14. ábra) rögzíti az E bizonyítékváltozók értékeit, és csak a maradék X és Y változókat mintavételezi. Ez garantálja, hogy minden generált esemény konzisztens a bizonyítékkal. Azonban nem minden esemény egyenlő. Mielőtt megállapítanánk a számlálási eredményeket a célváltozó eloszlásában, minden eseményt súlyozunk azzal a valószínűséggel, amely megadja, hogy az esemény mennyire van összhangban a bizonyítékkal. Ezt a valószínűséget az egyes bizonyítékváltozók feltételes valószínűségeinek a szorzatával mérjük, a szüleik ismeretében. Szemléletesen, azoknak az eseményeknek, ahol a bizonyíték valószínűtlennek tűnik, kisebb súlyt kell adni.

Alkalmazzuk az algoritmust a 14.11. (a) ábrán látható háló esetén a P(Eső∣Locsoló = igaz, VizesPázsit = igaz) kérdésre. A folyamat a következőképpen halad: először a w súlyt 1,0-ra állítjuk. Aztán generálunk egy eseményt:

w ← w × P(Locsoló = igaz∣Felhős = igaz) = 0,1

w ← w × P(VizesPázsit = igaz∣Locsoló = igaz, Eső = igaz) = 0,099

Itt a SÚLYOZOTT-MINTA az [igaz, igaz, igaz, igaz] eseményt adja ki 0,099 súllyal, és ezt az Eső = igaz esetnél vesszük számításba. A súly alacsony, mivel az esemény egy felhős napot ír le, amikor valószínűtlen, hogy a locsoló be van kapcsolva.

Hogy megértsük, miért is működik a valószínűségi súlyozás, azzal kezdjük, hogy megvizsgáljuk a SÚLYOZOTT-MINTA S_WS mintavételi eloszlását. Emlékezzünk, hogy az E bizonyítékváltozók értéke (e) rögzített. A többi változót Z-vel jelöljük, azaz Z = {X} ∪ Y. Az algoritmus Z minden változóját mintavételezi, szülei adott értékei mellett:

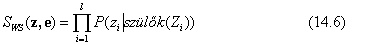
Vegyük észre, hogy a Szülők(Z_i) tartalmazhat mind rejtett, mind bizonyítékváltozókat is. A P(z) a priori eloszlástól eltérően az S_WS eloszlás szentel valamennyi figyelmet a bizonyítéknak is: a mintavételezett értékeket minden Z_i esetén befolyásolják a Z_i ősei között levő bizonyítékok. Másfelől, S_WS kevesebb figyelmet szentel a bizonyítékoknak, mint a P(z∣ e) valódi a posteriori eloszlás, mivel a mintavételezett értékek minden Z_i esetén figyelmen kívül hagyják azokat a bizonyítékokat, amelyek Z_i-nek nem ősei.^[150]

A w valószínűségi súly pótolja ki a különbséget a valódi és a kívánt mintavételi eloszlás között. Egy adott z-ből és e-ből álló x minta súlya az összes bizonyítékváltozó valószínűségének szorzata a szülei értékei mellett (amelyek közül néhány vagy akár az összes a Z_i-k között lehet):

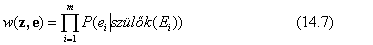
A (14.6) és (14.7) egyenleteket összeszorozva láthatjuk, hogy egy minta súlyozott valószínűsége különösen kényelmes alakú

mivel a két szorzat lefedi az összes változót a hálóban, lehetővé téve, hogy az együttes valószínűségre a (14.1) egyenletet használjuk.

Most már könnyen megmutatható, hogy a valószínűségi súlyozásos mintavétel konzisztens. Az X bármely konkrét x értékére a becsült a posteriori valószínűség a következőképpen számítható ki:

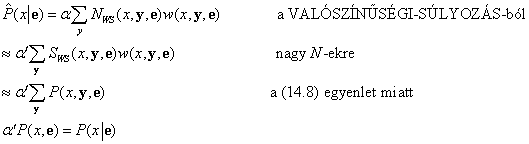
Így a valószínűségi súlyozás konzisztens becsléseket szolgáltat.

Mivel a valószínűségi súlyozás az összes generált mintát felhasználja, sokkal hatékonyabb lehet, mint az elutasításos mintavétel. Azonban a teljesítménye leromlik, amint a bizonyítékváltozók száma növekszik. Ez azért következik be, mert a legtöbb mintának nagyon kis súlya lesz, és így a súlyozott becslést főként a minták azon csekély töredéke határozza meg, amelyek egy elenyésző valószínűségnél jobban illeszkednek a bizonyítékokhoz. A probléma még erőteljesebben jelentkezik, ha a bizonyítékváltozók később fordulnak elő a változó sorrendben, mivel ekkor a minták olyan szimulációk, amelyek kevés hasonlóságot mutatnak a bizonyítékok által sugalmazott valósághoz.

Ebben a fejezetben a Markov lánc Monte Carlo (MCMC, Markov chain Monte Carlo) algoritmust ismertetjük, hogy Bayes-hálókban következtethessünk. Először leírjuk, mit is csinál az algoritmus, majd elmagyarázzuk, hogy miért is működik, és miért van ilyen bonyolult neve.

Az MCMC algoritmus

Az előző két mintavételi algoritmustól eltérően, amelyek az egyes eseményeket a semmiből generálják, az MCMC minden eseményt az azt megelőző esemény véletlen módosításával generál. Ezért a hálót hasznos úgy elképzelni, mint aminek van egy konkrét jelenlegi állapota, ami minden változóra meghatároz egy értéket. A következő állapot generálása egy X_i nem bizonyítékváltozóhoz tartozó érték véletlenszerű mintavételezésével történik, az X_i Markov-takarójába tartozó változók jelenlegi értékeinek feltétele mellett. (Emlékezzünk vissza az 14.2.2. szakasz - Feltételes függetlenségi relációk Bayes-hálókban részre: egy változó Markov-takarója a szüleiből, gyermekeiből és gyermekei szüleiből áll.) Az MCMC így véletlen bolyongást végez az állapottérben – a lehetséges teljes érték hozzárendelések terében –, egyszerre egy változót billentve át, de rögzítetten tartva a bizonyítékváltozókat.

Gondoljuk meg a P(Eső∣Locsoló = igaz, VizesPázsit = igaz) kérdést a 14.11. (a) ábrán látható háló esetén. A Locsoló és a VizesPázsit bizonyítékváltozók rögzítettek a megfigyelt értékeikre, míg a rejtett Felhős és Eső változók véletlenszerűen inicializáltak – mondjuk az egyik igaz-ra, a másik hamis-ra. Így a kezdeti állapot [igaz, igaz, hamis, igaz]. Ekkor a következő lépéseket hajtjuk végre ismétlődően:

A folyamat során meglátogatott minden egyes állapot egy olyan minta, ami hozzájárul az Eső célváltozó megbecsléséhez. Ha a folyamat 20 állapotot látogatott meg, ahol az Eső igaz, és 61 állapotot, ahol az Eső hamis, akkor a kérdésre a választ a NORMALIZÁL (〈20, 60〉) = 〈0,25, 0,75〉 adja. A teljes algoritmus a 14.15. ábrán látható.

Miért működik az MCMC?

Legyen q(x⟶x′) az a valószínűség, hogy a folyamat x állapotból x′ állapotba lép át. Ez az átmenet-valószínűség definiálja az úgynevezett Markov-láncot (Markov chain) az állapottéren. (A Markov-láncok a 15. és 17. fejezetben is kiemelkedő szerepet játszanak.)

Tegyük fel most, hogy t lépésnyit futtatjuk a Markov-láncot, és legyen π_t(x) annak a valószínűsége, hogy a rendszer a t időpillanatban az x állapotban van. Hasonlóan, legyen π_t=1(x′) annak a valószínűsége, hogy a rendszer t = 1 időpillanatban x′ állapotban van. Ismerve π_t(x)-et a π_t=1(x′) kiszámítható úgy, hogy minden olyan állapotra, amiben a rendszer t időpillanatban lehet, összegezzük az állapot valószínűségének és az ebből az állapotból az x′-be való átlépés valószínűségének szorzatát:

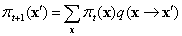
Akkor mondjuk, hogy egy lánc elérte a stacionárius eloszlását (stationary distribution), ha π_t = π_t+1. Jelöljük ezt a stacionárius eloszlást π-vel; az ezt definiáló egyenlet így

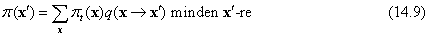
Ha a q átmenet-valószínűség eloszlás eleget tesz néhány alapvető feltevésnek,^[151] akkor bármely q esetén pontosan egyetlen π eloszlás elégíti ki ezt az egyenletet.

A (14.9) egyenlet úgy tekinthető, mint ami azt állítja, hogy az egyes állapotokból a „kilépések” várható értéke (azaz a jelenlegi „populáció”) egyenlő az összes állapotbóli „belépések” várható értékével. Ez a kapcsolat nyilvánvalóan teljesíthető, ha a várható átlépések mindkét irányban ugyanakkorák bármely állapotpár esetén. Ez a tulajdonság a teljes egyensúly (detailed balance):

π(x)q(x⟶x′) = π (x′)q(x⟶x′) minden x, x′-re (14.10)

Megmutathatjuk, hogy a teljes egyensúly maga után vonja a stacionaritást, egyszerűen az x-ek felett összegezve a (14.10) egyenletben. Azt kapjuk, hogy

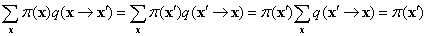
ahol az utolsó lépés abból következik, hogy x′-ből biztosan történik átmenet.

Most megmutatjuk, hogy az MCMC-KÉRDEZ mintavételi lépésében megadott q(x⟶x′) átmenet-valószínűség eleget tesz a teljes egyensúly egyenletének, ahol a stacionárius eloszlás a P(x∣e), a rejtett változók valódi a posteriori eloszlása. Ezt két lépésben teszszük meg. Először, egy Markov-láncot definiálunk, amelyben minden változót az öszszes többi változóval feltételesen mintavételezünk, és megmutatjuk, hogy ez eleget tesz a teljes egyensúly egyenletének. Majd egyszerűen megállapítjuk, hogy Bayes-hálóknál ez ekvivalens azzal a feltételes mintavételezéssel, hogy a feltétel a változó Markov-takarója (lásd 14.2.2. szakasz - Feltételes függetlenségi relációk Bayes-hálókban részben).

Legyen X_i a mintavételezett változó, és jelölje 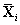az összes többi rejtett változót. A jelenlegi állapotban az értékük x_i és 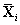. Ha az X_i-nek új x_i′ értéket mintavételezünk feltételesen az összes többi változóval, beleértve a bizonyítékot is, akkor

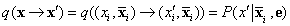
Ezt az átmenet-valószínűséget nevezik Gibbs-mintavételezőnek (Gibbs sampler), ami az MCMC egy nagyon kényelmes alakja.

Most megmutatjuk, hogy a Gibbs-mintavételező teljes egyensúlyban van a helyes a posteriori eloszlása szerint:

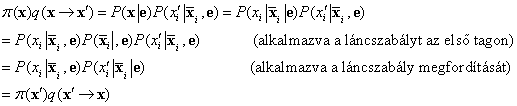
Ahogy az 14.2.2. szakasz - Feltételes függetlenségi relációk Bayes-hálókban részben kimondtuk, egy változó független az összes többi változótól a Markov-takarójának a feltételében; így:

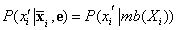
ahol mb(X_i) jelöli az X_i Markov-takarójában, MB(X_i)-ben lévő változók értékeit. Amint a 14.10. feladat mutatja, egy változó valószínűsége a Markov-takarójának ismeretében arányos a változó szüleivel vett feltételes valószínűségének és az egyes gyermekek azok szüleivel vett feltételes valószínűségeinek a szorzatával:

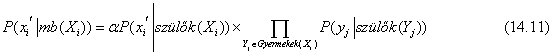
Így egy változó átléptetéséhez az X_i gyermekeinek számával megegyező számú szorzás szükséges.

Itt csupán az MCMC-nek egy egyszerű változatát tárgyaltuk, nevezetesen a Gibbs-mintavételezőt. Legáltalánosabb formájában az MCMC hatékony módszer valószínűségi modellekkel való számolásra, és számos változatát fejlesztették ki, közöttük a 4. fejezetben bemutatott szimulált lehűtés algoritmust, a 7. fejezetben a sztochasztikus kielégíthetőség algoritmust, valamint a 15. fejezetben a Metropolis–Hastings-mintavételezőt.