14.2. A Bayes-hálók szemantikája
Az előző alfejezetben bemutattuk a hálót, de annak jelentését nem. A Bayes-hálók szemantikáját kétféle módon lehet megérteni. Az első szerint a háló az együttes valószínűség-eloszlás függvény egy leírása. A második szerint a háló feltételes függetlenségekről szóló állítások együttesét írja le. A két szemlélet ekvivalens, de az első inkább abban segít, hogyan hozzunk létre egy hálót, míg a második a következtetési eljárások tervezését segíti.
A Bayes-háló a tárgytartomány teljes leírását adja meg. A benne található információk segítségével az együttes valószínűség-eloszlás függvény bármely bejegyzése kiszámítható.[145] Az együttes valószínűség-eloszlás függvény egy általános bejegyzése egy teljes – minden egyes változóhoz történő – hozzárendelés konjunkciójának a valószínűsége, úgymint P(X1 = x1 ∧ … ∧ Xn = xn). Erre a továbbiakban a P(x1, …, xn) rövidítést fogjuk használni. Egy bejegyzés értékét a következő egyenlőség adja meg:
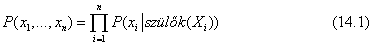
ahol a szülők(Xi) a Szülők(Xi)-ben szereplő változók adott értékeinek együttesét jelöli. Így az együttes valószínűség-eloszlás függvényt leíró táblázat minden bejegyzése a Bayes-hálóban szereplő, feltételes valószínűségi táblák (FVT) megfelelő elemeinek a szorzata. Ezzel az FVT-k valójában az együttes valószínűség-eloszlás függvény dekomponált leírását adják meg. Ennek illusztrálására kiszámítjuk annak az eseménynek a valószínűségét, hogy a riasztó megszólal, de nem volt sem betörés, sem földrengés, azonban János és Mária is telefonál. A kezdőbetűkkel jelölve a változókat:
P(j ∧ m ∧ a ∧ ¬b ∧ ¬e)
= P(j∣a)P(m∣a)P(a∣¬b ∧ ¬e)P(¬b)P(¬e)
= 0,90 × 0,70 × 0,001 × 0,999 × 0,998 = 0,00062
A 13.4. alfejezetben bemutattuk, hogy az együttes valószínűség-eloszlás függvény alapján a tárgytartománnyal kapcsolatos bármely kérdés megválaszolható. Ha egy Bayes-háló leírja az együttes valószínűség-eloszlás függvényt, akkor ez alapján bármely kérdés megválaszolható, összegezve a releváns együttes bejegyzéseket. A 14.4. alfejezet elmagyarázza, hogy ez hogyan végezhető el, azonban sokkal hatékonyabb módszereket is ismertet.
Egy módszer Bayes-hálók építésére
A (14.1) egyenlet definiálja, hogy mit is jelent egy adott Bayes-háló. Azonban arra nézve nem ad felvilágosítást, hogyan építhetünk olyan Bayes-hálót, hogy az általa meghatározott együttes valószínűség-eloszlás függvény az adott tárgytartomány megfelelő leírása legyen. Most megmutatjuk, hogy a (14.1) egyenlet tartalmaz bizonyos feltételes függetlenségi relációkat, amelyeket a tudásmérnök felhasználhat a háló topológiájának meghatározásánál. Elsőként írjuk fel az együttes valószínűség-eloszlás függvényt feltételes valószínűségek szorzataként, felhasználva a szorzatszabályt (lásd 13. fejezet):
P(x1, …, xn) = P(xn|xn–1, …, x1)P(xn–1, …, x1)
Majd ismételten alkalmazzuk ezt a lépést, minden egyes együttes valószínűséget felbontva egy feltételes valószínűségre és egy kisebb együttes valószínűségre. Végezetül egyetlen hosszú szorzatot kapunk:
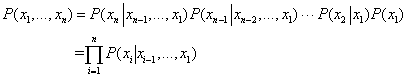
Ez a láncszabályként (chain rule) ismert azonosság valószínűségi változók bármely halmazára fennáll.
Összehasonlítva ezt a (14.1.) egyenlettel láthatjuk, hogy az együttes valószínűség-eloszlás függvény megadása ekvivalens azzal az általános állítással, hogy a háló minden Xi változójára
P(Xi|Xi–1, …, X1) = P(Xi|Szülők(Xi)) (14.2)
feltéve, hogy Szülők(Xi) ⊆ {Xi–1, …, X1}. Ez utóbbi feltétel a csomópontok bármely olyan sorszámozásával teljesíthető, ami konzisztens a gráf struktúrájából adódó implicit részleges rendezéssel.
Fontos
A (14.2) egyenlet szerint, egy Bayes-háló csak abban az esetben lehet helyes reprezentációja a tárgytartománynak, ha az adott szülők mellett, minden csomópont feltételesen független a csomópontot sorrendezésben őt megelőzőktől. Így a tárgytartomány struktúrájának megfelelő Bayes-háló megépítése során, minden egyes csomóponthoz úgy kell a szülőket megválasztanunk, hogy ez a feltétel teljesüljön. Szemléletesen ez azt jelenti, hogy az Xi csomópont szülei halmazának tartalmaznia kell az {X1, …, Xi–1} közül mindazokat a csomópontokat, amelyek közvetlenül befolyásolják Xi-t. Például tételezzük fel, hogy a 14.2. ábrán látható hálót már teljesen befejeztük, csupán a MáriaTelefonál szüleit kell még megválasztanunk. A MáriaTelefonál-t egyértelműen befolyásolja, hogy történt-e Betörés vagy Földrengés, de nem közvetlenül. A helyzettel kapcsolatos ismereteink alapján tudhatjuk, hogy ezek az események csak a riasztó által befolyásolhatják Mária telefonálással kapcsolatos viselkedését. Hasonlóan, ha a riasztó állapota ismert, akkor János hívásának bekövetkezte vagy elmaradása már nincs hatással Mária telefonálására. Formálisan fogalmazva, úgy véljük, hogy a következő feltételes függetlenség teljesül:
P(MáriaTelefonál|JánosTelefonál, Riasztás, Földrengés, Betörés)
= P(MáriaTelefonál|Riasztás)
Tömörség és a csomópontok sorrendje
Amellett hogy egy teljes és nem redundáns reprezentációja a tárgytartománynak, egy Bayes-háló gyakran sokkal tömörebb, mint az együttes valószínűség-eloszlás függvény. Ez a tulajdonsága teszi használhatóvá a sokváltozós tárgyterületek kezelésében. A Bayes-háló tömörsége a lokálisan strukturált (locally structured) (vagy ritka – sparse) rendszerek egy igen általános tulajdonságának példája. Egy lokálisan strukturált rendszerben egy komponens csak korlátos számú más komponenssel van kapcsolatban közvetlenül, függetlenül a komponensek teljes számától. Lokális struktúrákhoz általában inkább a lineáris, mint az exponenciális komplexitásnövekedés kapcsolható. A Bayes-háló esetében jogos azt feltételezni, hogy a legtöbb tárgytartomány esetén egy valószínűségi változót csak k számú más változó befolyásol, ahol k konstans. Ha bináris változókat tételezünk fel az egyszerűség kedvéért, akkor az egy csomóponthoz tartozó feltételes valószínűségi tábla megadásához legfeljebb 2k érték szükséges, így a teljes háló n2k értékkel megadható. Ezzel szemben az együttes valószínűség-eloszlás függvény 2n értéket tartalmaz. Egy konkrét példával élve, ha 30 csomópontunk van (n = 30), és mindegyiknek legfeljebb 5 szülője van (k = 5), akkor a Bayes-háló 960 számot igényel, míg az együttes valószínűség-eloszlás függvény több mint egy milliárdot.
Léteznek olyan tárgytartományok, ahol a változók mindegyikét közvetlenül befolyásolhatja az összes többi, így a háló teljesen összekötött. A feltételes valószínűségi táblák megadása ekkor ugyanakkora mennyiségű információt igényel, mint az együttes valószínűség-eloszlás függvény megadása. Bizonyos tárgytartományokban léteznek olyan gyenge függőségek, amiket feltétlenül modellezni kell egy új kapcsolat felvételével. De ha ezek a függőségek igen gyengék, akkor lehet, hogy nem éri meg a háló komplexitását megnövelni a pontosság kismértékű növelésének érdekében. Például a betöréses hálónkkal kapcsolatban kifogásolható az, hogyha földrengés van, akkor Mária és János akkor sem telefonálna, ha hallanák a riasztót, mivel feltételezik, hogy a földrengés okozta. Az, hogy hozzákapcsoljuk-e a Földrengés-t a MáriaTelefonál-hoz és a JánosTelefonál-hoz (és így megnöveljük a táblákat) azon múlik, hogy mennyire fontos pontosabb valószínűségeket kapni, és mennyire költséges meghatározni az extra információt.
Fontos
Azonban még egy lokálisan strukturált problémánál sem egyszerű lokálisan strukturált Bayes-hálót felépíteni. Ugyanis nemcsak azt követeljük meg, hogy minden egyes változót csak néhány másik befolyásoljon közvetlenül, hanem azt is, hogy a háló topológiája valóban mutassa azokat a közvetlen hatásokat a szülők megfelelő megválasztásával. A konstrukciós eljárásunk működése miatt előbb a „közvetlen befolyásolókat” kell a hálóhoz adni, ha azt szeretnénk, hogy szülőknek tudjuk őket választani az általuk befolyásolt csomópontnál. Ezért a helyes sorrend a csomópontok hozzáadásánál az, hogy először az „alapvető okokat” adjuk a hálóhoz, majd a változókat, amelyeket befolyásolnak, és ezt addig folytatjuk, amíg el nem érjük a „leveleket”, amelyeknek már nincs közvetlen okozati hatása más változókra.
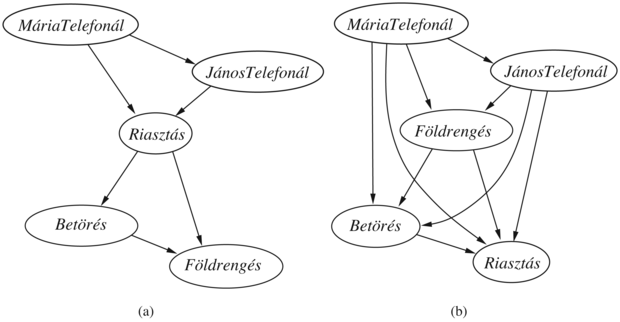
Mi történik, ha történetesen rossz sorrendet választunk? Vizsgáljuk meg újra a betöréses példát. Tételezzük fel, hogy a változókat a következő sorrendben adjuk a hálóhoz: MáriaTelefonál, JánosTelefonál, Riasztás, Betörés, Földrengés. Ekkor egy kicsit bonyolultabb hálót kapunk (14.3. (a) ábrán). Az eljárás a következő:
-
MáriaTelefonál hozzáadása: szülők nincsenek.
-
JánosTelefonál hozzáadása: ha Mária telefonál, az valószínűleg azt jelenti, hogy a riasztó megszólalt, ami természetesen valószínűbbé teszi, hogy János telefonáljon. Így a JánosTelefonál-nak szükségszerűen szülője a MáriaTelefonál.
14.3. ábra - A háló struktúrája függ a hozzáadás sorrendjétől. A csomópontokat mindegyik hálóhoz felülről lefelé haladva adtuk hozzá.
-
Riasztás hozzáadása: nyilvánvaló, ha mindketten telefonálnak, akkor valószínűbb, hogy a riasztó megszólalt, mintha csak egyikük, vagy egyikük sem. Így mind a JánosTelefonál, mind a MáriaTelefonál szükséges mint szülő.
-
Betörés hozzáadása: ha ismerjük a riasztó állapotát, akkor a Jánostól vagy Máriától jövő telefonhívások léte vagy hiánya csupán azt jelezhetik, hogy cseng-e a telefonunk, vagy hogy Mária zenéje hangosra van-e állítva, de a betörésről nem nyújtanak további információt. Azaz
P(Betörés∣Riasztás, JánosTelefonál, MáriaTelefonál) = P(Betörés∣Riasztás)
Így csak a Riasztás szükséges mint szülő.
-
Földrengés hozzáadása: ha a riasztó bekapcsolt, akkor valószínűbb, hogy bekövetkezett egy földrengés (mivel a riasztó valamiféle földrengésészlelő). De ha tudjuk, hogy betörés történt, akkor ez megmagyarázza a riasztást, és a földrengés valószínűsége csak picit nagyobb a normálisnál. Így a Betörés és a Riasztás is szükséges mint szülő.
Fontos
A kiadódó hálónak kettővel több éle van, mint az eredetinek a 14.2. ábrán, és hárommal több valószínűség meghatározását igényli. Ami még rosszabb, hogy néhány kapcsolódás megfoghatatlan viszonyt reprezentál, ami nehéz és nem természetes valószínűségi ítéleteket igényel, például a Földrengés feltételes valószínűségének a megbecslését, a Betörés és a Riasztás feltételekkel. Ez a jelenség igen általános, és kapcsolódik az okozati és diagnosztikai modelleknek a 8. fejezetben bevezetett megkülönböztetéséhez. Ha úgy próbálunk meg egy diagnosztikai modellt megépíteni, hogy a kapcsolatok okozat-ok irányúak (mint például a MáriaTelefonál-tól a Riasztás-ig vagy a Riasztás-tól a Betörés-ig kapcsolat), akkor végül egyébként független okok között kell függést meghatároznunk (és gyakran a különállóan bekövetkező okozatok között is). Ha ragaszkodunk az okozati modellhez, akkor kevesebb értéket kell megadnunk, és az értékeket általában könnyebb meghatározni. Orvosi tárgytartományon például Tversky és Kahneman demonstrálta, hogy orvos szakértők szívesebben hoznak valószínűségi ítéleteket okozati, mint diagnosztikai összefüggések esetén (Tversky és Kahneman, 1982).
A 14.3. (b) ábra a változók igazán szerencsétlen sorrendjét mutatja: MáriaTelefonál, JánosTelefonál, Földrengés, Betörés, Riasztás. Ez a háló 31 önálló valószínűség meghatározását igényli – pontosan annyit, amennyi a teljes együttes valószínűség-eloszlás függvény megadása. Azonban fontos felismerni, hogy a három háló bármelyike képes pontosan ugyanannak az együttes valószínűség-eloszlás függvénynek a reprezentálására. A két utóbbi egyszerűen csak nem reprezentálja az összes feltételes függetlenségi relációt, és így rengeteg szükségtelen érték meghatározására kényszerül.
A Bayes-hálókra egy „numerikus” szemantikát adtunk meg a teljes együttes eloszlás reprezentációjának a szempontjából, mint a (14.1) egyenletben. Ezt a szemantikát alkalmazva a Bayes-hálók konstrukciós módszereinek a származtatásánál azt a következményt kaptuk, hogy egy csomópont feltételesen független az őt megelőzőktől, ha a csomópont szülői adottak. Kiderül, hogy más módon is eljárhatunk. Elindulhatunk egy „topológiai” szemantikától, ami a gráf által kódolt feltételes függetlenségi relációkat adja meg, és ezekből származtatjuk a „numerikus” szemantikát. A topológiai szemantikát a következő két egymással ekvivalens meghatározás bármelyike rögzíti:[146]
-
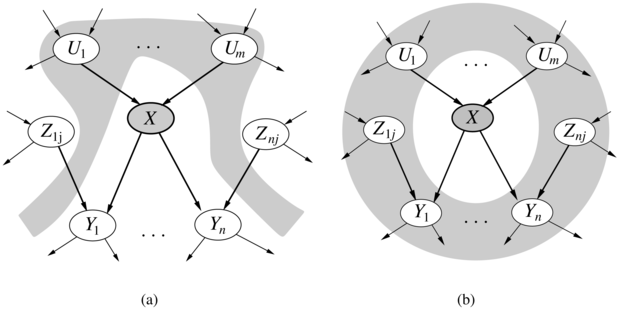
Egy csomópont feltételesen független a nem leszármazottaitól (non-descendants), feltéve, hogy a szülei adottak. Például a 14.2. ábrán JánosTelefonál független a Betörés-től és a Földrengés-től, ismerve a Riasztás értékét.
-
Egy csomópont feltételesen független az összes többi csomóponttól a hálózatban, a szülei, gyermekei és gyermeki szüleinek az ismeretében – azaz a Markov-takarójának (Markov blanket) ismeretében. Például, a Betörés független JánosTelefonál-tól és MáriaTelefonál-tól, a Betörés-t és Földrengés-t ismerve.
Ezeket a meghatározásokat mutatja be a 14.4. ábra. Ezekből a feltételes függetlenségi állításokból és az FVT-kből a teljes együttes eloszlást rekonstruálni lehet; így a „numerikus” szemantika és a „topológiai” szemantika ekvivalens.
14.4. ábra - (a) Az X csomópont feltételesen független a nem leszármazottaitól (Zij-ktől) a szülei (a szürke területen látható Ui-k) ismeretében. (b) Az X csomópont feltételesen független a háló összes többi csomópontjától a Markov-takarójának ismeretében (a szürke terület).
[145] A diszkrét változókra utaló szóhasználat ellenére az állítások analógjai folytonos változók esetén is fennállnak. (A ford.)
[146] Létezik egy további általános topológiai kritérium a d-elválasztás (d-separation) annak eldöntésére, hogy a csomópontok egy X halmaza független-e egy másik Y halmaztól egy harmadik Z halmaz feltétel esetén. A kritérium elég bonyolult, és nem szükséges a fejezetben az algoritmusok származtatásánál, ezért nem tárgyaljuk. A részletek megtalálhatók Russell és Norvig, valamint Pearl munkáiban (Russell és Norvig, 1995; Pearl, 1988). Shachter egy sokkal szemléletesebb módszert ad a d-elválasztások meghatározásához (Shachter, 1998).
