7.4. Az ítéletkalkulus: egy nagyon egyszerű logika
Most egy nagyon egyszerű logikát, az ítéletkalkulust (propositional logic) mutatjuk be.[67] Áttekintjük az ítéletkalkulus szintaxisát, majd a szemantikáját – annak a módját, ahogy a mondatok igazságát meghatározzuk. Azután megnézzük a maga után vonzást – a relációt egy adott mondat és azon mondat között, amelyik az előbbiből következik –, és megnézzük, hogy hogyan vezet ez egy egyszerű logikai következtetés algoritmushoz. Mindez természetesen a wumpus világban fog lejátszódni.
Az ítéletkalkulus szintaxisa meghatározza a lehetséges mondatokat. Az atomi mondatok (atomic sentences) – oszthatatlan szintaktikai elemek – egyetlen ítéletszimbólumból (proposition symbol) állnak. Minden ilyen szimbólum egy kijelentés, ami igaz vagy hamis lehet. Nagybetűs neveket fogunk használni a szimbólumok jelölésére: P, Q, R és így tovább. A nevek tetszőlegesek, de gyakran úgy választjuk őket, hogy a nevek bizonyos jelentéssel is rendelkezzenek. Például használhatjuk a W1,3-t annak az állításnak a kifejezésére, hogy a wumpus az [1, 3]-ban van. (Ne felejtsük el, hogy a W1,3 atomi, így a W, az 1 és a 3 nem jelentéssel bíró részei a szimbólumnak.) Létezik két ítéletszimbólum, amelyeknek rögzített az értelmezése: az Igaz egy mindig igaz állítás, és a Hamis egy mindig hamis állítás.
Összetett mondatok (complex sentences) létrehozhatók egyszerűbb mondatokból logikai összekötőjelek (logical connectives) felhasználásával. Öt elterjedten használt összekötőjel van:
¬ (nem). Egy mondatot, mint a ¬W1,3-t, negációnak (negation) nevezünk. Egy literál (literal) vagy egy atomi mondat (egy pozitív literál), vagy egy negált atomi mondat (egy negatív literál).
∧ (és). Egy mondatot, amelynek fő kötőszava a ∧, mint például a W1,3 ∧ C1,3 konjunkció-nak (conjunction) nevezünk; ennek részei a konjunktok (conjuncts). (Az ∧ jel hasonlít egy A-ra, az angol And (és) szóból.)
∨ (vagy). Egy mondat, amely használja a ∨ összekötőjelet, mint a (W1,3 ∧ C1,3) ∨ W2,2 egy diszjunkció (disjunction), méghozzá a (W1,3 ∧ C1,3) és a W2,2 diszjunktoknak (disjuncts) a diszjunkciója. (Történelmileg a ∨ jel a latin vel kifejezésből származik, ami „vagy”-ot jelent. A legtöbb ember számára könnyebb megjegyezni úgy, mint egy fejjel lefelé álló és jelet, vagy a magyar olvasók számára, mint a vagy szó első betűjét.)
⇒(implikáció). Egy mondatot, mint amilyen a (W1,3 ∧ C1,3) ⇒ ¬W2,2 implikációnak (implication) (vagy feltételes mondatnak) nevezünk. Ennek premisszája (premise) vagy előzménye (antecedent) a (W1,3 ∧ C1,3), konklúziója (conclusion) vagy következménye (consequent) pedig a ¬W2,2 implikáció szabályként (rule) vagy ha–akkor (if–then) állításként is ismert. Az implikációt más könyvekben időnként a ⊃ vagy a → szimbólumokkal jelölik.
⇔ (akkor és csakis akkor). A W1,3 ⇔¬W2,2 mondat egy ekvivalencia (biconditional).
A 7.7. ábra mutatja az ítéletkalkulus formális nyelvtanát; ha nem ismeri a BNF jelölésrendszert, akkor nézze meg az 1. szakasz - B1. Nyelvek definiálása Backus–Naur-Formában (BNF) részt.
Vegyük észre, hogy a nyelvtan nagyon szigorú a zárójelezésnél: minden mondatot, amelyet bináris összekötőjellel hozunk létre, zárójelek közé kell tenni. Ez biztosítja, hogy a szintaxis teljesen egyértelmű. Ez azt is jelenti például, hogy ((A ∧ B) ⇒ C)-t kell írjunk A ∧ B ⇒ C helyett. Az olvashatóság javítása céljából gyakran elhagyjuk a zárójeleket, megbízva ehelyett az összekötőjeleknek egy precedencia-sorrendjében. Ez hasonló az aritmetikában alkalmazott precedenciához – például az ab + c-t ((ab) + c)-nek olvassuk, és nem a(b + c)-nek, mert a szorzásnak magasabb a precedenciája, mint az összeadásnak. Az ítéletkalkulus precedencia-sorrendje (a legmagasabbtól a legalacsonyabb felé: ¬, ∧, ∨, ⇒ és ⇔. Így a mondat:
¬P ∨ Q ∧ R ⇒ S
ekvivalens a következő mondattal:
((¬P) ∨ (Q ∧ R)) ⇒ S
A precedencia nem oldja fel a többértelműséget az olyan mondatoknál, mint az A ∧ B ∧ C, amelyet olvashatunk ((A ∧ B) ∧ C)-ként vagy (A ∧ (B ∧ C))-nek. Mivel a mondatnak ez a két olvasása ugyanazt jelenti a következő részben definiálandó szemantika szerint, az olyan mondatok, mint az A ∧ B ∧ C megengedettek. Szintén megengedjük az A ∨ B ∨ C és az A ⇔ B ⇔C mondatokat. Olyan mondatok, mint az A ⇒ B ⇒ C nem megengedettek, mert a két olvasásnak különböző jelentései vannak, ebben az esetben ragaszkodunk a zárójelhez. Végül, néha használni fogunk szögletes zárójelet az egyszerű zárójel helyett, ami a mondatot áttekinthetőbbé teszi majd.
Most, hogy specifikáltuk az ítéletkalkulus szintaxisát, definiáljuk a szemantikáját is. A szemantika definiálja a szabályokat, amivel meghatározható a mondat igazsága egy bizonyos modellben. Az ítéletkalkulusban a modell egyszerűen az igazságértéket – igaz vagy hamis – rögzíti minden ítéletszimbólumra. Például ha a tudásbázis mondatai a C1,2, C2,2 és C3,1 ítéletszimbólumokat használják fel, akkor egy lehetséges modell:
m1 ={C1,2 = hamis, C2,2 = hamis, C3,1 = igaz}
Három ítéletszimbólum esetén 23 = 8 lehetséges modell van – pontosan azok, amelyek a 7.5. ábrán vannak feltüntetve. Vegyük észre azonban, hogy miután elköteleztük magunkat egy szintaxis mellett, a modellek tisztán matematikai objektumokká váltak, amelyeknek nem feltétlenül van kapcsolatuk a wumpus világgal. A C1,2 csak egy szimbólum, jelentheti azt, hogy „csapda van az [1, 2]-ben” vagy azt, hogy „Párizsban vagyok ma és holnap”.
Az ítéletkalkulus szemantikájának meg kell határoznia, hogyan számítsuk ki bármely mondat igazságértékét egy adott modellben. Ez rekurzívan történik. Minden mondat atomi mondatokból és az ötféle összekötőjelből lett létrehozva, így meg kell határoznunk, hogy hogyan számítsuk ki az atomi mondatok igazságát, és meg kell határoznunk azt is, hogy hogyan számítsuk ki az igazságát az egyes összekötőjelek felhasználásával formált összetett mondatnak. Az atomi mondatok esete egyszerű:
-
Igaz akkor, ha minden modellben igaz, és Hamis akkor, ha minden modellben hamis.
-
Minden más ítéletszimbólumnak az igazságértékét közvetlenül a modellben kell meghatározni. Például a korábban megadott m1 modellben a C1,2 hamis.
Összetett mondatokra olyan szabályaink vannak, mint
-
Bármely s mondatra és bármely m modellre, a ¬s mondat az m-ben akkor és csakis akkor igaz, ha s hamis m-ben.
Az ilyen szabályok visszavezetik az összetett mondatok igazságának eldöntését egyszerűbb mondatokra. Minden összekötőjelre vonatkozó szabály összefoglalható egy igazságtáblában (truth table), amely meghatározza egy összetett mondat igazságértékét a mondat komponenseinek minden lehetséges igazságérték hozzárendeléseihez. Az öt logikai összekötőjel igazságtábláját mutatja a 7.8. ábra. Ilyen táblák felhasználásával bármely s mondat igazságértéke egy m modellre vonatkozóan kiszámolható rekurzív kiértékelések egyszerű folyamatával. Például a ¬C1,2 ∧ (C2,2 ∨ C3,1) mondatot kiértékelve m1-ben igaz ∧ (hamis ∨ igaz) = igaz ∧ igaz = igaz értéket kapunk. A 7.3. feladat azt kéri, hogy írjon egy IK-IGAZ? (s,m) algoritmust, amely kiszámítja az s ítéletkalkulus mondatnak az igazságértékét egy m modellben.
Korábban azt mondtuk, hogy a tudásbázist mondatok halmaza alkotja. Most láthatjuk, hogy egy logikai tudásbázis ilyen mondatok konjunkciója. Tehát ha egy üres TB-vel kezdünk, és végrehajtjuk a KIJELENT(TB, S1), ..., KIJELENT (TB, Sn) műveleteket, akkor a TB = S1 ∧ …∧ Sn áll elő. Ez azt jelenti, hogy tudásbázisokat és mondatokat egymással felcserélhetően használhatunk.
Az „és”, „vagy” és „nem” igazságtáblái eltérnek attól, amit a természetes nyelvi jelentésük alapján gondolnánk. A lehetséges félreértés legszembetűnőbb pontja, hogy a P ∨ Q kifejezés igaz akkor is, ha mind P, mind Q is igaz. Létezik másik összekötőjel is, a „kizáró vagy”-nak nevezett jel (röviden xor), amely hamisat ad, ha mindkét diszjunkt igaz.[68] Nincs általános egyetértés az „exkluzív vagy” szimbólumát illetően; két jelölés is ismert: 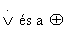
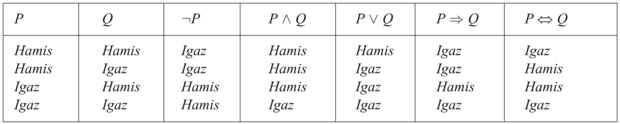
Az implikáció (⇒) igazságtáblája rejtélyesnek tűnhet első látásra, mivel nem teljesen illeszkedik ösztönös megértésünkhöz, hogy „P implikálja Q-t” vagy „ha P, akkor Q”. Az ítéletkalkulus nem kíván semmilyen ok-okozati relációt vagy relevanciát P és Q között. A mondat: „az a tény, hogy 5 páratlan implikálja, hogy Tokió Japán fővárosa” az ítéletkalkulusnak egy igaz mondata (a normális interpretáció szerint), még akkor is, ha ez határozottan furcsa mondatnak tűnik. Egy másik esete a félreértéseknek, hogy bármely implikáció igaz, ha az előzménye hamis. Például az „az az állítás, hogy 5 páros szám, implikálja, hogy Samu okos” mondat igaz, függetlenül attól, hogy Samu okos-e. Ez bizarrnak tűnik, de elfogadható, ha a „P ⇒ Q”-t úgy értelmezzük, hogy „ha P igaz, akkor azt állítom, hogy Q is igaz. Egyébként nem állítok semmit”. Az egyetlen eset, amikor ez a mondat hamis, ha P igaz, de Q hamis.
A P ⇔ Q ekvivalencia igazságtáblája azt mutatja, hogy akkor igaz, ha mind P ⇒ Q és Q ⇒ P igaz. Ezt gyakran úgy írjuk le, hogy „P akkor és csakis akkor, ha Q” vagy matematikában szokták jelölni „P aa Q”-nak. A wumpus világ szabályait legjobban az ⇔ használatával tudjuk felírni. Például, egy négyzet szellős, ha a szomszédos, ha a szomszédos négyzetben csapda van, és egy négyzet csakis akkor szellős négyzetben csapda van. Így ekvivalenciákra van szükségünk, mint a
S1,1 ⇔ (C1,2 ∨ C2,1)
ahol S1,1 jelenti, hogy szellő van az [1, 1]-ben. Vegyük észre, hogy az egyirányú implikáció
S1,1 ⇒ (C1,2 ∨ C2,1)
igaz a wumpus világban, de nem teljes. Nem szabályozza azokat a modelleket, amelyekben S1,1 hamis és C1,2 igaz, amivel megszegnénk a wumpus világ szabályait. Egy másik mód ennek érzékeltetésére, hogy az implikáció igényli a csapda jelenlétét, ha szellő van, miközben az ekvivalencia szintén megkívánja a csapda hiányát, ha nincs szellő.
Most, hogy definiáltuk az ítéletkalkulus szemantikáját, létre tudunk hozni egy tudásbázist a wumpus világ számára. Az egyszerűség kedvéért csak a csapdákkal fogunk törődni, a wumpust magát feladatként az olvasóra hagyjuk. A tudás, amelyet most leírunk, elégséges ahhoz, hogy elvégezzük a 7.3. alfejezetben nem formálisan már elvégzett következtetést.
Először meg kell választanunk a szótárunkat az ítéletszimbólumaink megnevezéséhez. Minden i, j-re:
-
Legyen Ci,j igaz, ha csapda van [i, j]-ben.
-
Legyen Si,j igaz, ha szellő van [i, j]-ben.
A tudásbázis tartalmazza a következő mondatokat (mindegyiket felcímkézzük a kényelem kedvéért):
-
Nincs csapda az [1, 1]-ben:
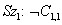
-
Egy négyzet akkor és csakis akkor szellős, ha csapda van a szomszédos négyzetben. Ezt minden négyzetre vonatkozóan ki kell jelenteni, mi most csak a releváns négyzeteket tekintjük:
Sz2: S1,1 ⇔ (C1,2 ∨ C2,1)
Sz3: S2,1 ⇔ (C1,1 ∨ C2,2 ∨ C3,1)
-
Az eddigi mondatok minden wumpus világban igazak. Most hozzáadjuk a szellő érzetet az első két meglátogatott négyzetre abban a specifikus világban, ahol az ágens jelenleg tartózkodik, ami elvezet a 7.3. (b) ábrán látott szituációhoz.
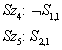
A tudásbázis most Sz1-től Sz5-ig tartalmaz mondatokat. Tekinthetjük ezt úgy is, mint egyetlen mondatot – az Sz1 ∧ Sz2 ∧ Sz3 ∧ Sz4 ∧ Sz5 konjunkciót –, mivel ez azt is kijelenti egyben, hogy minden egyes mondat is igaz.
Emlékezzünk, hogy a logikai következtetés célja, hogy eldöntsük, hogy TB ⊨ α bizonyos α mondatokra. Például, hogy a tudásbázis maga után vonzza-e a C2,2 állítást. Az első algoritmusunk a következtetésre a vonzat definíciójának közvetlen megvalósítása lesz: vegyük sorba a modelleket, és ellenőrizzük, hogy α igaz-e minden modellben, amelyben a TB igaz. Az ítéletlogikában a modellek az igaz és hamis értékek hozzárendelései minden egyes ítéletszimbólumhoz. Visszatérve a mi wumpus világbeli példánkhoz, a releváns ítéletszimbólumok az S1,1, S1,2, C1,1, C1,2, C2,1, C2,2, C3,1. A 7 szimbólum 27 = 128 lehetséges modellt jelent, háromban ezek közül a TB igaz (7.9. ábra). Ebben a három modellben 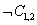 igaz, így nincsen csapda az [1, 2]-ben. Viszont a C2,2 a három modellből kettőben igaz és egyben hamis, így még nem tudjuk megmondani, hogy van-e csapda [2, 2]-ben.
igaz, így nincsen csapda az [1, 2]-ben. Viszont a C2,2 a három modellből kettőben igaz és egyben hamis, így még nem tudjuk megmondani, hogy van-e csapda [2, 2]-ben.
A 7.9. ábra precízebb formában megismétli a 7.5. ábrán illusztrált következtetést. A 7.10. ábra egy általános algoritmust mutat a maga után vonzás eldöntésére az ítéletkalkulusban. Mint a VISSZALÉPÉSES-KERESÉS algoritmus a 3.4.3. szakasz - Mélységi keresés részben, az IT-VONZAT? egy rekurzív felsorolást végez a változó hozzárendelések véges terén. Az algoritmus helyes, mivel közvetlenül a vonzat definícióját valósítja meg, és teljes, mivel bármely TB-on és α mondaton működik, és mindig sikeresen véget ér, hiszen véges számú modellt kell megvizsgálni.
![A tudásbázis alapján épített igazságtábla látható az ábrán. A TB igaz, ha Sz1-től és Sz5-ig igaz, amely a 128 sorból csak 3-ban fordul elő. Mind a 3 sorban C1,2 hamis, tehát nincsen csapda az [1, 2]-ben. Viszont lehet, hogy van csapda [2, 2]-ben (bár lehet, hogy nincs).](/mi_almanach/sites/default/files/books/35/files/kepek/07-09.png)
IK-IGAZ? igazat ad vissza, ha a mondatot tartalmazza a modell. A modell változó reprezentál egy részleges modellt, egy hozzárendelést a változók egy részéhez. A KIEGÉSZÍT (P, igaz, modell) függvény egy új részleges modellt ad vissza, amelyben P értéke igaz.
Fontos
Természetesen a „véges számosság” nem mindig jelenti a „néhányat”. Ha a TB és az α mondat összesen n szimbólumot tartalmaz, akkor 2n modell létezik. Így az algoritmus időigénye O(2n). (A tárigénye csak O(n), mivel a felsorolás mélységi jellegű.) A fejezet későbbi részében fogunk látni olyan algoritmusokat, amelyek sokkal hatékonyabbak a gyakorlatban. Sajnos minden ismert, az ítéletlogikára vonatkozó következtetési algoritmusnak a legrosszabb esetre vonatkozó komplexitása exponenciálisan függ a bemenetek számától. Nem remélhetjük, hogy ennél hatékonyabbak is lehetnénk, mivel az ítéletlogikában a maga után vonzás co-NP-teljes (lásd A) függelék).
Mielőtt belemerülnénk a logikai következtetés részleteinek tárgyalásába, szükségünk van néhány további, a vonzattal kapcsolatos fogalomra. Mint a vonzat, ezek a fogalmak is a logika minden formájára alkalmazhatók, de legjobban egy konkrét logikán – mint amilyen az ítéletkalkulus – lehet illusztrálni őket.
Az első fogalom a logikai ekvivalencia (logical equivalence): két mondat, az α és a β mondatok logikailag ekvivalensek, ha ezek a mondatok a modellek ugyanazon halmazán igazak. Ezt úgy jelöljük, hogy α ⇔ β. Például (igazságtáblákat használva) könnyen megmutathatjuk, hogy P ∧ Q és Q ∧ P logikailag ekvivalensek; további ekvivalenciák láthatók a 7.11. ábrán. Az ekvivalenciák nagyon hasonló szerepet játszanak a logikában, mint az aritmetikai identitások a közönséges matematikában. Az ekvivalencia alternatív definíciója a következő: bármely két α, β mondatra,
α ≡ β akkor és csakis akkor, ha α ⊨ β és β ⊨ α
(Emlékeztetőül, a ⊨ a maga után vonzást jelöli.)
A második fogalom, amelyre szükségünk lesz az érvényesség (validity). Egy mondat érvényes, ha igaz minden modellben. Például a 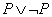 mondat érvényes. Az érvényes mondatokat tautológiáknak (tautologies) is szokták nevezni, ezek szükségszerűen igazak és így feleslegesek. Mivel az Igaz mondat igaz minden modellben, minden érvényes mondat logikailag ekvivalens az Igaz mondattal.
mondat érvényes. Az érvényes mondatokat tautológiáknak (tautologies) is szokták nevezni, ezek szükségszerűen igazak és így feleslegesek. Mivel az Igaz mondat igaz minden modellben, minden érvényes mondat logikailag ekvivalens az Igaz mondattal.

Fontos
Mire jók akkor az érvényes mondatok? A vonzatokra vonatkozó definíciónk alapján levezethetjük a dedukcióelméletet (deduction theorem), amelyet már az ókori görögök is ismertek:
Bármely α és β mondatra α ⊨ β akkor és csakis akkor, ha az (α ⇒ β) mondat érvényes.
(A 7.4. feladatban ennek a bizonyítását kérjük.) A 7.10. ábrán látható következtetési algoritmust úgy tekinthetjük, mint a (TB ⇒ α) érvényességének ellenőrzését. Másik oldalról nézve viszont minden érvényes implikáció leír egy legitim következtetést.
Az utolsó fogalom, amelyre szükségünk lesz a kielégíthetőség (satisfiability). Egy mondat kielégíthető, ha igaz néhány modellben. Például a korábban bemutatott tudásbázis, az (Sz1 ∧ Sz2 ∧ Sz3 ∧ Sz4 ∧ Sz5), kielégíthető, mert van három olyan modell, amelyben igaz, ahogy ezt a 7.9. ábrán megmutattuk. Ha egy α mondat igaz az m modellben, akkor azt mondjuk, hogy m kielégíti (satisfies) α-t, vagy m egy modellje α-nak. A kielégíthetőség ellenőrizhető úgy, hogy a lehetséges modelleket felsoroljuk mindaddig, amíg nem találunk egyet, amely kielégíti a mondatot. A mondatok kielégíthetőségének meghatározása az ítéletlogikában az első olyan probléma volt, amelyről bebizonyították, hogy NP-teljes.
Számos probléma a számítástechnikában valójában kielégíthetőségi probléma. Például a kényszerkielégítési problémák az 5. fejezetben alapvetően arra kérdeznek rá, hogy a kényszerek kielégíthetők-e néhány hozzárendeléssel. Megfelelő transzformációk után a keresési problémák szintén megoldhatók a kielégíthetőség ellenőrzésével. Az érvényesség és a kielégíthetőség természetesen kapcsolatban vannak: α érvényes akkor és csakis akkor, ha 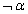 nem kielégíthető; és fordítva, α akkor és csakis akkor kielégíthető, ha
nem kielégíthető; és fordítva, α akkor és csakis akkor kielégíthető, ha 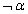 nem érvényes. A következő hasznos eredményt is ismerjük:
nem érvényes. A következő hasznos eredményt is ismerjük:
α ⊨ β akkor és csakis akkor, ha az (α ∧ ¬ β) nem kielégíthető
Fontos
A β mondat bizonyítása α alapján, az (α ∧ ¬β) kielégíthetetlenségének ellenőrzésével, pontosan megfelel a szokásos matematikai bizonyítási technikának a redukcio ad absurdumnak (szó szerint „redukció egy abszurd dologra”). Szokták ezt megcáfolás (refutation) általi bizonyításnak is nevezni vagy bizonyítás ellentmondás (contradiction) által. Feltételezzük, hogy a β mondat hamis, és megmutatjuk, hogy ez a feltételezés ellentmondásra vezet az ismert α axiómákkal. Ez az ellentmondás pontosan azt jelenti, mint amikor azt mondjuk, hogy az (α ∧ ¬β) mondat kielégíthetetlen.


