3.4. Nem informált keresés
Ez az alfejezet öt keresési stratégiát tárgyal, amelyek a nem informált (vaknak is nevezett) keresés (noninformed (blind) search) cím alá sorolhatók. A kifejezés azt jelenti, hogy ezen stratégiáknak semmilyen információjuk nincs az állapotokról a probléma definíciójában megadott információn kívül. Működésük során mást nem tehetnek, mint a következő állapotok generálása és a célállapot megkülönböztetése a nem célállapottól. Azokat a stratégiákat, amelyek tudják, hogy az egyik közbülső állapot „ígéretesebb”, mint egy másik közbülső állapot, informált keresési (informed search) vagy heurisztikus keresési (heuristic search) stratégiának nevezzük. Ezeket majd a 4. fejezet tárgyalja. A keresési stratégiákat a csomópontok kifejtési sorrendje különbözteti meg egymástól.
A szélességi keresés (breadth-first search) egy egyszerű keresési stratégia, ahol először a gyökércsomópontot fejtjük ki, majd a következő lépésben az összes a gyökércsomópontból generált csomópontot, majd azok követőit stb. Általánosságban a keresési stratégia minden adott mélységű csomópontot hamarabb fejt ki, mielőtt bármelyik, egy szinttel lejjebbi csomópontot kifejtené.
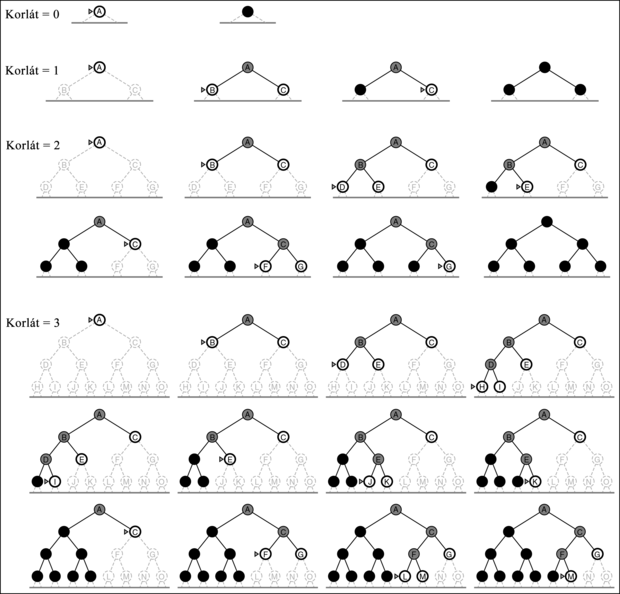
A szélességi keresést meg lehet valósítani a FA-KERESÉS algoritmussal egy olyan üres peremmel, amely egy először-be-először-ki (first-in-first-out – FIFO) sor, biztosítva ezzel, hogy a korábban meglátogatott csomópontokat az algoritmus korábban fejti ki. Más szóval a FA-KERESÉS (probléma, FIFO-SOR ()) meghívása szélességi keresést eredményez. A FIFO sor az összes újonnan legenerált követőt a sor végére teszi, magyarán a sekélyebb csomópontok korábban kerülnek kifejtésre, mint a mélyebben fekvők. A 3.10. ábra illusztrálja a keresés előrehaladását egy egyszerű bináris fa esetén.

A szélességi keresés elemzéséhez az előbbi részben tárgyalt négy jellemzőt fogjuk használni. Könnyű belátni, hogy ez a keresés teljes. Ha a legsekélyebb célcsomópont valamilyen véges d mélységben fekszik, a szélességi keresés eljut hozzá az összes nála sekélyebben fekvő csomópontot kifejtve (feltéve persze, hogy a b elágazási tényező véges). A legsekélyebb célcsomópont nem szükségképpen optimális. Pontosabban a szélességi keresés optimális, ha az útköltség a csomópont mélységének nem csökkenő függvénye (például ha minden cselekvésnek ugyanannyi a költsége).
Eddig a szélességi keresésnek csak a jó tulajdonságait láttuk. Ahhoz, hogy megértsük miért nem mindig ezt a stratégiát választjuk, meg kell vizsgálnunk a keresés végrehajtásához szükséges idő és memória mennyiségét. Ehhez egy olyan hipotetikus állapotteret veszünk alapul, amelyben minden egyes állapotot kifejtve b új állapot keletkezik. A keresési fa gyökércsomópontja b csomópontot generál az első szinten, amelyek mindegyike újabb b csomópontot, összesen b2 csomópontot generál a második szinten. Ezek mindegyike újabb b csomópontot generál, összesen b3 csomópontot a harmadik szinten és így tovább. Tételezzük fel, hogy ezen probléma megoldása d mélységben található. Ekkor a legrosszabb esetben a d-edik szinten az utolsót kivéve (mert a célt magát nem fejtjük ki) a csomópontok mindegyikét ki kell fejtenünk, a (d + 1)-edik szinten bd+1 – b csomópontot generálva. A generált csomópontok össz-száma így:
b + b2 + b3 + … + bd + (bd+1– b) = O(bd+1)
Minden legenerált csomópontot a memóriában el kell tárolni, mert vagy a perem eleme, vagy egy perembeli csomópont őse. A tárigény így az időigénnyel azonos (meg egy további csomópont a gyökér számára).
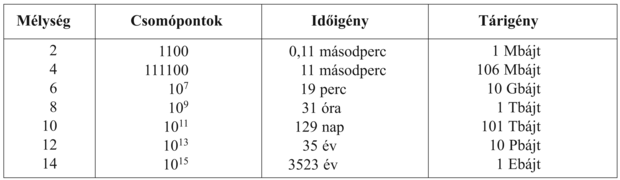
Azok, akik járatosak a komplexitáselemzésben, kezdenek aggódni (vagy izgatottak lesznek, ha szeretik a kihívásokat), amikor exponenciális komplexitást látnak, mint amilyen például az O(bd+1). A 3.11. ábra megmutatja, hogy miért. Az ábra egy b = 10 elágazási tényezővel rendelkező szélességi keresést mutat a d megoldás mélység több értékére. A táblában feltételezzük, hogy másodpercenként 10 000 csomópontot generálunk, illetve egy csomópont tárolásához 1000 bájtra van szükség. Számos feladvány jellegű probléma felel meg ezeknek a feltételezéseknek (egy 100-as tényezővel ide vagy oda), ha azokat modern személyi számítógépeken futtatjuk.
Fontos
A 3.11. ábra alapján két tanulságot vonhatunk le. Először is a szélességi keresés esetén a tárigény nagyobb problémát jelent az időigénynél. A legtöbb ember, amennyiben érdekli a válasz egy fontos problémára, türelmesen ki tud várni 31 órát, hogy egy 8 mélységű keresés lefusson, de csak kevés számítógépnek van a kereséshez szükséges Tbájtnyi memóriája. Szerencsére léteznek ennél kevesebb memóriát igénylő keresési algoritmusok is.
Fontos
A második tanulság, hogy az időigény még mindig fontos tényező. Ha a problémánk 12 mélységű, akkor (a feltételezéseink mellett) a szélességi keresésnek (vagy akármlyik nem informált keresési algoritmusnak) 35 évbe telne a megoldás megtalálása. Általánosságban az exponenciális komplexitású keresési problémák közül csak a legkisebb problémapéldányok oldhatók meg.
A szélességi keresés optimális, ha minden lépés költsége azonos, mert mindig a legsekélyebb ki nem fejtett csomópontot fejti ki. Egyszerű általánosítással egy olyan algoritmust találhatunk ki, amely tetszőleges lépésköltség mellett optimális. Az egyenletes költségű keresés (uniform cost search) mindig a legkisebb útköltségű n csomópontot fejti ki először, nem pedig a legkisebb mélységű csomópontot. Egyszerűen belátható, hogy a szélességi keresés is egyenletes költségű keresés, amennyiben minden lépésköltség azonos.
Az egyenletes költségű keresés nem foglalkozik azzal, hogy hány lépésből áll egy bizonyos út, hanem csak az összköltségükkel törődik. Emiatt mindig végtelen hurokba kerül, ha egy csomópont kifejtése zérus költségű cselekvéshez és ugyanahhoz az állapothoz való visszatérést eredményez (például a NoOp cselekvés). A teljességet csak úgy garantálhatjuk, hogy minden lépés költsége egy kis pozitív e konstansnál nagyobb, vagy azzal egyenlő. Ez a feltétel egyben az optimalitás elégséges feltétele is. Ez azt jelenti, hogy egy út költsége az út mentén mindig növekszik. Ebből a tulajdonságból látszik, hogy az algoritmus a csomópontokat mindig a növekvő útköltség függvényében fejti ki. Azaz az első kifejtésre kiválasztott célcsomópont egyben az optimális megoldás is (emlékezzünk arra, hogy a FA-KERESÉS a célállapottesztet csak a kifejtésre megválasztott csomópontokra alkalmazza). Javasoljuk, hogy próbálják ki az algoritmust, hogy a Bukarestbe vezető legrövidebb utat megtalálják.
Az egyenletes költségű keresést nem a mélység, hanem az útköltség vezérli, így komplexitását a b és a d függvényében nehéz jellemezni. Helyette legyen C∗ az optimális megoldás költsége, és tételezzük fel, hogy minden cselekvés költsége legalább e. Az algoritmus idő- és tárigénye legrosszabb esetben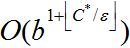 , ami sokkal több lehet, mint bd. Ez azért lehetséges, mert az egyenletes költségű keresés képes (és sokszor ezt meg is teszi) a kis lépésekből álló nagy fákat felkutatni a nagy és feltehetően hasznos lépéseket tartalmazó utak előtt. Amikor minden lépés költsége ugyanannyi, az
, ami sokkal több lehet, mint bd. Ez azért lehetséges, mert az egyenletes költségű keresés képes (és sokszor ezt meg is teszi) a kis lépésekből álló nagy fákat felkutatni a nagy és feltehetően hasznos lépéseket tartalmazó utak előtt. Amikor minden lépés költsége ugyanannyi, az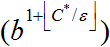 , persze azonos bd-nel.
, persze azonos bd-nel.
A mélységi keresés (depth-first search) mindig a keresési fa aktuális peremében a legmélyebben fekvő csomópontot fejti ki. A keresés lefolyását a 3.12. ábra illusztrálja. A keresés azonnal a fa legmélyebb szintjére jut el, ahol a csomópontoknak már nincsenek követőik. Kifejtésüket követően kikerülnek a peremből és a keresés „visszalép” ahhoz a következő legmélyebben fekvő csomóponthoz, amelynek vannak még ki nem fejtett követői.
Ez a stratégia egy olyan FA-KERESÉS függvénnyel implementálható, amelynek a sorbaállító függvénye az utolsónak-be-elsőnek-ki (last-in-first-out, LIFO), más néven verem. A mélységi keresést szokás a FA-KERESÉS függvény alternatívájaként egy rekurzív függvénnyel is implementálni, amely a gyermekcsomópontokkal meghívja önmagát (mélységkorláttal dolgozó rekurzív mélységi keresés algoritmusát a 3.13. ábra mutatja).
A mélységi keresés nagyon szerény tárigényű. Csak egyetlen, a gyökércsomóponttól egy levélcsomópontig vezető utat kell tárolnia, kiegészítve az út minden egyes csomópontja melletti kifejtetlen csomópontokkal. Egy kifejtett csomópont el is hagyható a memóriából, feltéve, hogy az összes leszármazottja meg lett vizsgálva. Egy b elágazási tényezőjű és m maximális mélységű állapottér esetén a mélységi keresés tárigénye bm + 1. A 3.11. ábra feltételezéseivel élve és feltételezve, hogy a célcsomópont mélységű csomópontoknak nincsenek követőik, azt találjuk, hogy például d = 12 mélység esetén a mélységi keresés 118 kbájtot igényelne a 10 Pbájttal szemben, ami tízmilliárdos redukciót jelent a tárigényben.
A mélységi keresés visszalépéses keresésnek (backtracking search) nevezett változata még kevesebb memóriát használ. A visszalépéses keresés az összes követő helyett egyidejűleg csak egy követőt generál. Minden részben kifejtett csomópont emlékszik, melyik követője jön a legközelebb. Ily módon csak O(m) memóriára van szükség, O(bm) helyett. A visszalépéses keresés még egy memória- (és idő-) spóroló trükkhöz folyamodik. Az ötlet a követő csomópont generálása az aktuális állapot módosításával, anélkül hogy az állapotot átmásolnánk. Ezzel a memóriaszükséglet egy állapotra és O(m) cselekvésre redukálódik. Ahhoz, hogy az ötlet működjön, amikor visszalépünk, hogy a következő követőt generáljuk, mindegyik módosítást vissza kell tudnunk csinálni. Nagy állapottérrel rendelkező problémák esetén, mint például robot-összeszerelés esetén, az ilyen módszerek lényegesek a sikerességhez.
A mélységi keresés hátrányos tulajdonsága, hogy egy rossz választással egy hosszú (akár végtelen) út mentén lefelé elakadhat, miközben például egy más döntés elvezetne a gyökérhez közeli megoldáshoz. A 3.12. ábrán például a mélységi keresés kifejti az egész bal oldali részfát, annak ellenére, hogy a C csomópont a megoldás. Ha a J csomópont szintén megoldás lenne, a mélységi keresés azt adná vissza megoldásul, következésképpen a mélységi keresés nem optimális. Ha a bal oldali részfa korlátlanul mély lenne és nem tartalmazna megoldást, a mélységi keresés soha nem állna meg, következésképpen a mélységi keresés nem teljes. A legrosszabb esetben a mélységi keresés a keresési fában az összes O(bm) csomópontot generálni fogja, ahol m a csomópontok maximális mélysége. Jegyezzük meg, hogy m sokkal nagyobb lehet, mint d (a legsekélyebb megoldás mélysége), és korlátlan fák esetén értéke végtelen.
A végtelen fák problémáját a mélységi keresés azáltal küszöböli ki, hogy az utak maximális mélységére egy ℓ korlátot ad. Az ℓ mélységben lévő csomópontokat úgy kezeli, mintha nem is lennének követőik. A módszer neve a mélységkorlátozott keresés, MKK (depth-limited search, DLS). A mélységkorlát a végtelen út problémáját ugyan megoldja, de a nemteljesség egy újabb forrását hozza be, ha ℓ < d -t választunk, azaz, ha a legsekélyebb célcsomópont a mélységkorláton túl van (ez nem is esélytelen, ha d eleve ismeretlen). A mélységkorlátozott keresés ℓ > d választással sem lesz optimális. A keresés időigénye O(bℓ), tárigénye O(bℓ). A mélységi keresés egy olyan speciális mélységkorlátozott keresésének tekinthető, amelynek mélységkorlátja ℓ = ∞.
A mélységi korlátot néha a probléma ismeretére lehet alapozni. Például Románia térképén 20 város található, így tudjuk, hogy ha létezik egy megoldás, az maximálisan 19 lépés hosszú lehet, így az ℓ = 19 egy lehetséges választás. Ha azonban a térképet tüzetesebben tanulmányoznánk, felfedeznénk, hogy minden város bármelyik másik városból legfeljebb 9 lépésben elérhető. Ez a szám, amit az állapottér átmérőjének (diameter) nevezünk, jobb mélységkorlátot ad, ami hatékonyabb mélységkorlátozott keresést eredményez. A legtöbb probléma esetén azonban mindaddig nem tudunk jó mélységkorlátot adni, amíg meg nem oldottuk a problémát.
A mélységkorlátozott keresést az általános fakeresési vagy a rekurzív mélységi keresési algoritmus egyszerű módosításával lehet implementálni. A 3.13. ábra mutatja a rekurzív mélységkorlátozott keresés pszeudokódját. Jegyezzük meg, hogy a mélységkorlátozott keresés kudarccal kétféle módon állhat le: a standard kudarc csomópont jelzi a megoldás hiányát, a vágás érték viszont jelzi a megoldás mélységkorláton belüli hiányát.
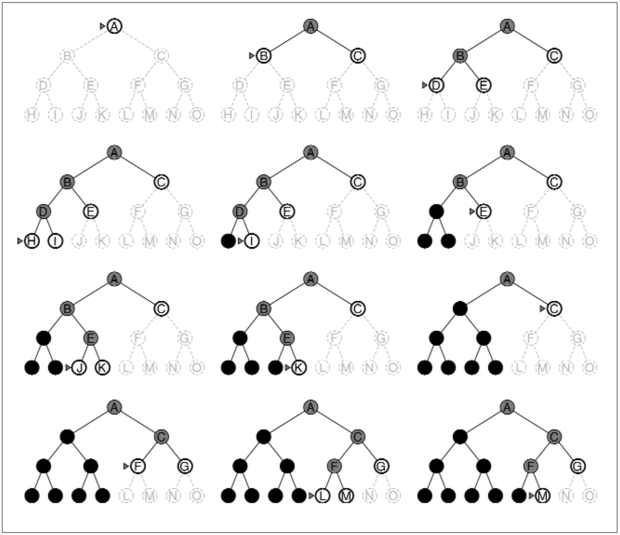
Az iteratívan mélyülő keresés (iterative deepening search) – vagy iteratívan mélyülő mélységi keresés – egy általános stratégia, amit sokszor a mélységi kereséssel együtt alkalmaznak a legjobb mélységkorlát megtalálására. Az algoritmus képes erre, mert fokozatosan növeli a mélységkorlátot – legyen az először 0, majd 1, majd 2 stb. – amíg a célt meg nem találja. Ez akkor következik be, ha a mélységkorlát eléri a d-t, a legsekélyebben fekvő célcsomópont mélységét. Az algoritmust a 3.14. ábra mutatja. Az iteratívan mélyülő keresés ötvözi a szélességi és a mélységi keresés előnyös tulajdonságait. A mélységi kereséshez hasonlóan szerény, pontosabban O(bd) memóriaigénnyel rendelkezik. A szélességi kereséshez hasonlóan teljes, ha elágazási tényezője véges, és optimális, ha az útköltség a csomópontok mélységének nem csökkenő függvénye. A 3.15. ábra az ITERATÍVAN-MÉLYÜLŐ-KERESÉS első négy iterációját mutatja egy bináris fán, ahol az algoritmus a megoldást a negyedik iterációban találja meg.
Az iteratívan mélyülő keresés tékozlónak tűnhet, mert felettébb sok állapotot többször is kifejt. Kiderül azonban, hogy a költségtöbblet nem lényeges. Ennek az az oka, hogy egy olyan keresési fában, ahol minden szinten ugyanaz (vagy közel ugyanaz) az elágazási tényező, majdnem az összes csomópont a legmélyebb szinten található, így nem túl sokat számít, hogy a magasabb szinteket többször is kifejtjük. Az iteratívan mélyülő keresésben a legmélyebb szinten (d mélység) található csomópontokat csak egyszer fejtjük ki, egy szinttel feljebb kétszer stb. egészen a gyökér gyerekeiig, amelyeket d-szer fejtünk ki. Így a kifejtett csomópontok össz-száma:
Cs(IMK) = (d)b + (d – 1)b2 + ... + (1)bd
amely O(bd) időkomplexitást eredményez. Összehasonlításul nézzük meg a szélességi keresés által generált csomópontok számát:
Cs(SZK) = b + b2 + ... + bd + (bd+1 – b)
Vegyük észre, hogy a szélességi keresés d + 1 mélységben is generál csomópontokat, az iteratívan mélyülő kereséssel ellentétben. Ennek eredménye, hogy az iteratívan mélyülő keresés a szélességi keresésnél gyorsabb, annak ellenére, hogy a csomópontokat többször fejti ki. Konkretizálva, például b = 10 és d = 5 esetén ezek a számok:
Cs(IMK) = 50 + 400 + 3000 + 20 000 + 100 000 = 123 450
Cs(SZK) = 10 + 100 + 1000 + 10 000 + 100 000 + 999 990 = 1 111 100
Fontos
Általánosságban nagy keresési térrel rendelkező problémák esetén és ha a megoldás mélysége nem ismert, a nem informált módszerek köréből az iteratívan mélyülő keresés a javasolt.

Az iteratívan mélyülő keresés a szélességi kereséssel abban rokon, hogy minden iterációban a csomópontok teljes rétegét megvizsgálja, mielőtt a következő rétegre térne rá. Hasznosnak látszik az egyenletes költségű keresés iteratív változatának kifejlesztése, amely örökölné ez utóbbi optimalitását, mellőzve annak a tárkövetelményeit. Az ötlet a növekvő útköltségkorlát használata a növekvő mélységkorlát helyett. Az eredményül kapott algoritmussal, amelynek neve iteratívan megnyúló keresés (iterative lengthening search) a 3.11. feladat foglalkozik. Sajnos az derül ki, hogy az iteratívan megnyúló keresés overheadje tekintélyes az egyenletes költségű kereséshez képest.
A kétirányú keresés mögött az az ötlet húzódik, hogy egyszerre el lehet indítani egy keresést előrefelé a kiinduló állapotból, illetve hátrafelé a célállapotból, és a keresés akkor fejeződik be, ha a két keresés valahol találkozik (lásd 3.16. ábra). Az érv az, hogy bd/2 + bd/2 sokkal kisebb, mint bd, illetve az ábrán szemlélve, hogy a két kisebb kör összterülete kisebb, mint annak a nagy körnek a területe, amelynek középpontja a kiinduló állapot, és amely a peremével a célállapotot eléri.
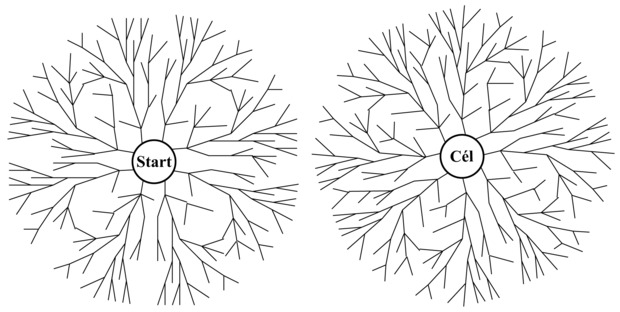
A kétirányú keresést úgy implementálják, hogy az egyik vagy mindkét keresés egy csomópont kifejtése előtt megvizsgálja, hogy az nem része-e a másik keresési fa peremének. Ha igen, megvan a cél. Ha a probléma például d = 6 megoldás mélységű, és mindegyik irányban a szélességi keresést futtatjuk csomópontonként, a két keresés a legrosszabb esetben akkor találkozik, ha mindegyik algoritmus a 3-as mélységben egy csomópont kivételével minden csomópontot kifejtett. A b = 10 esetén ez 22 200 csomópont generálását jelenti a standard szélességi keresés által generált 1 111 111 csomóponthoz képest. Annak ellenőrzését, hogy egy csomópont a másik keresési fához tartozik-e, egy hash-táblával konstans időben meg lehet oldani. A kétirányú keresés időkomplexitása így O(bd/2). Legalább az egyik keresési fát a memóriában kell tartani, hogy a tartozás ellenőrzése kivitelezhető legyen, a tárkomplexitás tehát szintén O(bd/2). Ez a tárkomplexitás a kétirányú keresés legnagyobb gyengéje. Ha mindkét keresés szélességi keresés, az algoritmus teljes és optimális (egyenletes költség esetén). Más módszerek kombinációja vagy a teljesség, vagy az optimalitás, vagy mindkettő elvesztéséhez vezethet.
Az időkomplexitás mérséklése a kétirányú keresést igen vonzóvá teszi, de mit is jelent a célállapotból hátrafelé keresni? Ez nem is olyan egyszerű, mint amilyennek hangzik. Legyenek x csomópont elődcsomópontjai (predecessors), az Előd(x)-ek azon csomópontok, amelyek mindegyikének x a követő csomópontja. A kétirányú keresés feltételezi, hogy egy Előd(x) hatékonyan számítható. Legegyszerűbb az az eset, amikor az összes cselekvés az állapottérben reverzíbilis, így Előd(x) = Követő(x). Más esetben azonban igen nagy ötletességre lehet szükség.
Nézzük most, hogy mit is jelent az, hogy „cél”, ha a célállapotból hátrafelé kell keresni. A 8-as kirakójáték és a romániai útkeresés esetén egyetlenegy célállapot létezik csak, így a hátrafelé keresés és az előrefelé keresés igen hasonlítanak egymásra. Amennyiben létezik a célállapotoknak egy explicit listája, mint például a 3.3. ábra két koszmentes célállapota, akkor megkonstruálhatunk egy olyan ál-célállapotot, amelynek közvetlen követői az aktuális célállapotok. Más módon, néhány redundáns csomópont-generálás elkerülhető azzal, hogy a célállapotok halmazát egyetlenegy célállapotnak tekintjük, amelynek minden elődje szintén egy állapothalmaz – konkrétan azon állapotok halmaza, amelyek követője a célállapothalmaz eleme (lásd még 3.6. alfejezet).
A kétirányú keresés szempontjából a legnehezebb eset, amikor a célállapottesztnél a feltehetően nagy célállapothalmazról csak implicit leírás áll rendelkezésünkre, például a sakkban az összes állapot, ami kielégíti a „matt” célt. A hátrafelé keresésnek az „m1 cselekvés révén a »matt« állapotba vezető összes állapot” tömör leírását kellene tudnia megkonstruálni, és hasonló módon folytatni. E leírásokat az előrefelé haladó keresés által generált állapotokkal kellene tesztelni. Ennek nincs általánosan hatékony módja.
A 3.17. ábra a 3.4. alfejezetben megfogalmazott négy kiértékelési kritérium tükrében összehasonlítja a keresési stratégiákat.