6.2. Optimális döntések kétszemélyes játékokban
A kétszemélyes játékokkal fogunk foglalkozni, ahol a két játékost – a hamarosan nyilvánvalóvá váló okból – MAX-nak és MIN-nek fogjuk hívni. MAX lép először, majd a játékosok felváltva lépnek, amíg a játék véget nem ér. A játék végén a győztes játékos pontokat kap (vagy néha a vesztes kap büntetőpontokat). A játékot formálisan egyfajta keresési problémaként lehet definiálni az alábbi komponensekkel:
-
A kiinduló állapot (initial state), ami magában foglalja a táblaállást, valamint azt, hogy ki fog lépni.
-
Egy állapotátmenet-függvény (successor function), amely (lépés, állapot) párok listájával tér vissza, megadva a legális lépéseket és az azokból következő állapotokat.
-
Egy végteszt (terminal test), ami meghatározza, hogy a játéknak mikor van vége. Azok az állapotok, ahol a játék befejeződött, a végállapotok (terminal states).
-
Egy hasznosságfüggvény (utility function, amit nyereségfüggvénynek – payoff function – is neveznek) a játék végeredményéhez egy számértéket rendel. A sakkban a végeredmény győzelem, vereség vagy döntetlen lehet, amit a +1, –1 és 0 értékekkel ábrázolhatunk. Néhány játék ennél több végeredményre vezethet. Például az ostáblában a nyereség +192 és –192 között változhat. Ebben a fejezetben főleg a zérusösszegű játékokkal foglalkozunk, bár a nem zérusösszegű játékokat is megemlítjük.
MAX lép először, egy X-et téve valamelyik üres négyzetbe. A keresési fa egy részét mutatjuk, MIN (O) és MAX váltakozó, egymást követő lépéseit megadva, amíg el nem érjük a végállapotokat, melyekhez a játék szabályai szerint lehet hasznossági értékeket hozzárendelni.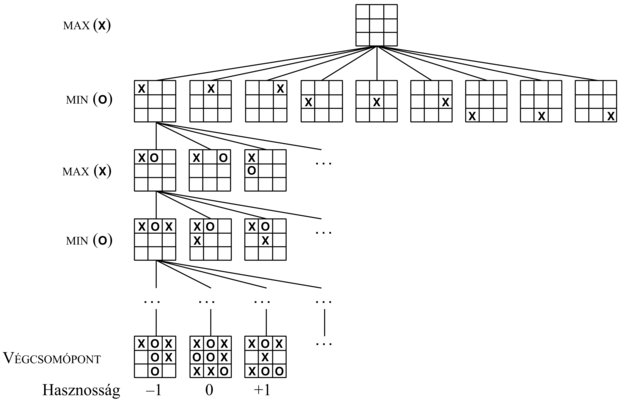
A kezdeti állapot és mindkét fél legális lépései a játék játékfáját (game tree) definiálják. A 6.1. ábra a 3 × 3-as amőbajáték keresési fájának egy részét mutatja. Kezdeti állapotban MAX-nak kilenc lehetséges lépése van. A játék során MAX és MIN felváltva tesznek X-et illetve O-t, míg egy végállapotnak megfelelő levélcsomópontba el nem jutnak, ahol az egyik játékosnak egy sorban, egy oszlopban vagy az egy átló mentén három O-ja vagy X-e lesz, vagy minden négyzet ki lesz töltve. Az egyes levélcsomópontok alatt található számok a végcsomópontnak a MAX szempontjából mért hasznosságát jelölik. A nagy értékekről feltételezzük, hogy jók MAX számára és rosszak MIN számára (amiből a játékosok neve is ered). MAX feladata, hogy a játékfát (és főleg a végállapotok hasznosságát) a legjobb lépés meghatározására használja fel.
Egy normális keresési problémánál, az optimális megoldás nem lenne más, mint a célállapothoz vezető lépések szekvenciája – azaz egy olyan végállapothoz vezető lépésszekvencia, amely a győzelmet jelenti. Egy játékban azonban MIN-nek is van beleszólása a dologba. Ezért MAX-nak egy olyan stratégiát (strategy) kell találnia, amely meghatározza MAX lépését a kezdeti állapotban, majd a MIN lehetséges válaszaiból keletkező állapotokban, majd ismét MAX lépéseit a MIN erre vonatkozó lehetséges válaszaiból keletkező állapotokban és így tovább. Nagyjából azt lehet mondani, hogy egy optimális stratégia olyan kimenetelekhez vezet, amelyek legalább olyan jók, mintha bármilyen más stratégiával egy tévedhetetlen opponens ellen játszanánk. Először megmutatjuk, hogyan kell megkeresni az optimális stratégiát, bár ennek kiszámítására MAX-nak általában nem lesz elegendő ideje az amőbánál bonyolultabb játékokban.
Még egy olyan egyszerű játék, mint az amőba is túl bonyolult ahhoz, hogy megmutassuk a teljes keresési fát, ezért áttérünk a 6.2. ábrán látható abszolút triviális játékra. MAX lehetséges lépéseit a1-gyel, a2-vel és a3-mal címkéztük meg. Az a1-re MIN lehetséges válaszait a b1, b2, b3 stb. jelölik. Ez a konkrét játék MAX és MIN egy-egy lépése után véget ér. (A játékok nyelvén azt mondjuk, hogy ez a fa egy lépés mély és két fél lépésből vagy lépésváltásból (ply) áll.) A végcsomópontok hasznossága ebben a játékban 2 és 14 közé esik.
MAX lépéseit, míg a ∇ csomópontok MIN lépéseit jelölik. A végcsomópontok a hasznossági függvénnyel számított hasznossági értékeket MAX szemszögéből mutatják, míg a többi csomópontnál a minimax értékét jelöltük be. MAX legjobb lépése a gyökérben a1, mert ez vezet a legmagasabb minimax értékű követőhöz. MIN legjobb válasza b1, mert ez vezet a minimális minimax értékű követőhöz.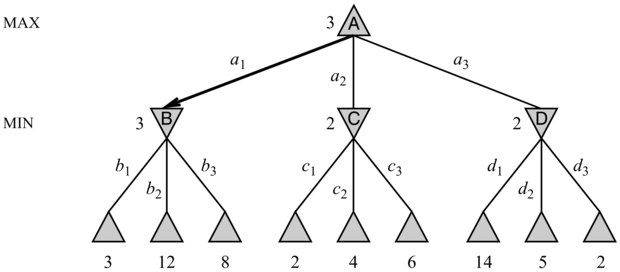
Adott játékfa mellett az optimális stratégia meghatározásához az egyes csomópontok minimax értékét kell megvizsgálni, amit MINIMAX-ÉRTÉK (n)-ként írunk le. Egy csomópont minimax értéke a csomópont hasznossága MAX szemszögéből, feltéve, hogy innen kezdve egészen a játék befejezéséig mindkét játékos optimálisan lép. Egy végállapot minimax értéke természetesen a saját hasznossága. Továbbá, adott minimax értékek mellett, MAX szeretne a maximális értékű, MIN pedig a minimális értékű állapotba jutni. Rendelkezünk tehát az alábbi függvénnyel:
|
|
||
|
|
ha n egy végállapot, |
|
|
maxs∈Követők(n) |
ha n egy |
|
|
mins∈Követők(n) |
ha n egy |
|
Alkalmazzuk ezeket a definíciókat a 6.2. ábrán látható játékfára. Az ábra alján lévő célállapotokat már felcímkéztük hasznossági értékükkel. Az első, B címkéjű, MIN csomópontnak három követője van 3, 12 és 8 értékkel, a B csomópont minimax értéke tehát 3. Hasonlóan a két másik MIN csomópontnak 2 a minimax értéke. A gyökér egy MAX csomópont; a követőinek minimax értékei 3, 2, és 2, így a gyökér minimax értéke 3. Azonosíthatjuk a gyökér minimax döntését (minimax decision) is. MAX számára az a1 cselekvés az optimális választás, mert maximális értékű követőhöz vezet.
Ezen optimális játékdefiníció MAX számára feltételezi, hogy MIN is optimálisan játszik – hiszen a dolgok kimenetelét MAX számára a legrosszabb esetre kivetítve maximalizálja. Mi van azonban, ha MIN nem játszik optimálisan? Ekkor könnyű belátni (6.2. feladat), hogy MAX még jobban jár. Szuboptimális ellenféllel szemben sok stratégia elképzelhető, amely az optimálisnál jobb, azonban ezek a stratégiák rosszabbnak fognak bizonyulni optimális ellenfelekkel szemben.
A minimax algoritmus (minimax algorithm) (6.3. ábra) az optimális döntést az aktuális állapotból számítja ki, felhasználva az egyes követő állapotok minimax értékeinek kiszámítására a definiáló egyenletekből közvetlenül származtatott, egyszerű rekurzív formulát. A rekurzió egészen a falevelekig folytatódik, majd a minimax értékeket a fa mentén visszafelé terjesztjük (back-up), ahogy a rekurzió visszalép. A 6.2. ábrán például az algoritmus először rekurzív módon leereszkedik a három bal alsó csomóponthoz, a HASZNOSSÁG függvénnyel kiszámítva, hogy az értékek rendre 3, 12, és 8. Majd az algoritmus előveszi ezen értékek minimumát, azaz 3-t, és ezt adja vissza, ahogy a B csomóponthoz visszatér. Hasonló procedúra eredményezi a további visszaadott értékeket: 2-t a C és 2-t a D csomópont számára. Végül vesszük a 3, 2 és 2 értékek maximumát, hogy a gyökér által visszaadott 3-as értéket megkaphassuk.
A minimax algoritmus a játékfa teljes mélységi feltárását végzi. Ha a fa maximális mélysége m, és minden csomópontban b legális lépés létezik, akkor a minimax algoritmus időkomplexitása O(bm). A tárkomplexitása O(bm) egy olyan algoritmus számára, amely az összes követőt egyszerre számítja ki, és O(m) egy olyan algoritmus esetében, amely a követőket egyenként generálja 3.4.3. szakasz - Mélységi keresés. Valós játékok esetén ez az időkomplexitás az algoritmust teljesen haszontalanná teszi, az algoritmus azonban jó alap a játékok matematikai elemzéséhez és a gyakorlati szempontból alkalmasabb algoritmusokhoz.
MAX-ÉRTÉK és MIN-ÉRTÉK függvények végigmennek a teljes játékfán, le egészen a levélcsomópontokig, hogy meghatározzák a csomópont felfelé terjesztett értékét.
Számos elterjedt játékban több játékos is részt vehet, nem csupán kettő. Vizsgáljuk meg, hogy a minimax ötletet hogyan terjeszthetjük ki többszemélyes játékok esetére. Technikai szempontból a dolog egyszerű, azonban felmerül néhány érdekes koncepcionális kérdés.
Először is egy csomópontokhoz rendelt egyetlen értéket egy értékvektorral kell felváltani. Például egy háromszemélyes játékban, ahol három játékos, A, B és C vesz részt, minden csomóponttal egy 〈vA, vB, vC〉 vektort társítunk. Végállapotok esetén ez a vektor megadja az állapot hasznosságát minden játékos szemszögéből (kétszemélyes zérusösszegű játékokban a kételemű vektort egy értékre le lehet egyszerűsíteni, mert az értékek mindig ellentétesek). Ezt a kibővítést legjobb úgy implementálni, hogy a HASZNOSSÁG függvény adja vissza a hasznosságok vektorát.
Most a nem terminális állapotokkal foglalkozunk. Nézzük meg a 6.4. ábrán látható játékfában az X jelzésű csomópontot. Ebben az állapotban a C játékos dönti el, hogy mit csináljon. Egyik választása a 〈vA = 1, vB = 2, vC = 6〉, míg a másik a 〈vA = 4, vB = 2, vC = 3〉 vektorokkal rendelkező végállapothoz vezet. Mivel 6 több, mint 3, C-nek az első lépést kellene választania. Ez azt jelenti, hogy ha a játék az X csomópontot eléri, a következő lépés a 〈vA = 1, vB = 2, vC = 6〉 hasznosságú végállapothoz fog vezetni. X visszaadott értéke így ez a vektor. Általánosságban egy n csomópont visszaadott értéke annak a követőnek a hasznosságvektora, amely követőnek az n csomópontnál választó játékos szempontjából legnagyobb az értéke.
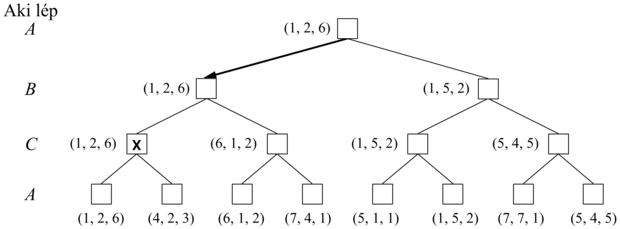
Mindenki, aki olyan többszemélyes játékokat játszik, mint például a DiplomacyΤΜ, gyorsan meggyőződhet, hogy a kétszemélyes játéknál sokkal többről van itt szó. Többszemélyes játékban a játékosok között általában lehetségesek formális vagy informális szövetségek (aliances). A játék előrehaladtával szövetségek köttetnek és bontatnak fel.
Hogyan is kellene értelmezni egy ilyen viselkedést? Természetes következménye-e a szövetség az egyes játékosok optimális stratégiáinak egy többjátékos játékban? Úgy tűnik, hogy ez igaz lehet. Tegyük fel például, hogy A és B gyengén, míg C erősebben áll. Akkor néha optimális mind A, mind B számára, ha nem egymást, hanem C-t támadják meg, hogy az egyenként ne végezzen velük. Ily módon az együttműködés tisztán egoista viselkedésből is kialakulhat. Persze ahogy az együttes támadásnak kitett C gyengül, a szövetség értéke csökken, és vagy A, vagy B a megegyezést megszegheti. Egyes esetekben az explicit szövetségek az úgyis bekövetkezendő eseményeket rögzítik konkrét módon. Más esetekben szociális megbélyegzés jár a szövetség megszegéséért, így a játékosnak mérlegelnie kell a szövetség megszegésének rövid idejű előnyét és a szavahihetetlenként való megbélyegzés hosszú távú hátrányát. (Az ilyen bonyodalmakról többet a 17.6. alfejezetben.)
Ha a játék nem zérusösszegű, akkor együttműködés két játékos esetén is létrejöhet. Tegyük fel például, hogy létezik olyan végállapot, amelynek hasznossága 〈vA = 1000, vB = 1000〉, és 1000 mindkét játékos számára az elérendő legnagyobb hasznosság. A két játékos optimális stratégiája akkor az, hogy ennek az állapotnak az elérése érdekében mindent megtesznek – azaz a két játékos automatikusan kooperálni fog, hogy a kölcsönösen előnyös célt elérjék.

