4.2. Heurisztikus függvények
Ebben a részben a 8-as kirakójátékhoz keresünk heurisztikus függvényeket, hogy rávilágítsunk a heurisztikus függvények általános természetére.
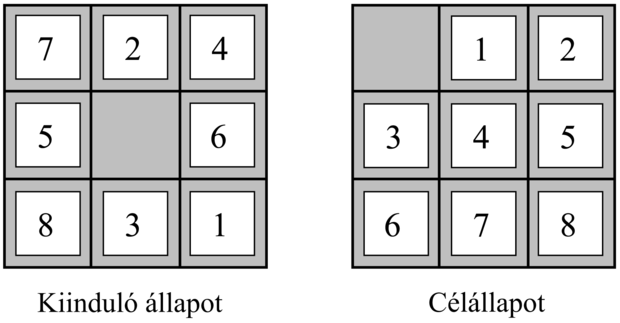
A 8-as kirakójáték a legrégebbi heurisztikus keresési feladatok egyike. Mint azt a 3.2. alfejezetben láttuk, a játék lényege, hogy a számozott lapkákat vízszintesen és függőlegesen az üres helyre tolva a kiindulóállásból a célállásba jussunk (lásd 4.7. ábra).
Egy átlagos megoldás véletlen módon generált 8-as kirakójáték példányok esetén kb. 22 lépésből áll. Az elágazási tényező nagyjából 3 (amikor az üres lapka középen van, akkor négy, amikor a sarokban van, akkor kettő, és amikor valamelyik szélső középső pozícióban van, akkor pedig három mozgatás lehetséges). Ebből adódóan egy 22 mélységig menő kimerítő keresés közelítőleg 322 ≈ 3,1 × 1010 állapotot vizsgálna meg. Az ismétlődő állapotok nyilvántartásával ezt a számot 170 000-ed részére le lehet csökkenteni, mert csak 9!/2 = 181 440 különböző elérhető elrendezés létezik (lásd 3.4. feladat). Ez egy kezelhető szám, azonban ugyanez a szám a 15-ös kirakójáték esetén már durván 1013, így a következő teendő egy jó heurisztika megkeresése. Amennyiben a legrövidebb megoldásokat akarjuk megtalálni A* bevetésével, olyan heurisztikus függvényre van szükségünk, ami soha sem becsüli túl a célállapot eléréséhez szükséges lépések számát. Az ilyen heurisztikák keresésének a 15-ös kirakójáték esetén nagy a múltja. Íme két lehetséges függvény:
-
h1 = a rossz helyen lévő lapkák száma. A 4.7. ábrán a 8 lapkából egyik sincs a helyén, így a kiinduló állapotban h1 = 8 lenne. h1 elfogadható heurisztikus függvény, mivel nyilvánvaló, hogy minden rossz helyen lévő lapkát legalább egyszer mozgatni kell.
-
h2 = a lapkáknak a saját célhelyeiktől mért távolságaik összege. Mivel a lapkákat nem lehet átlók mentén mozgatni, az általunk kiszámított távolság a vízszintes és függőleges távolságok összege lesz. Ezt néha háztömb- (city block distance) vagy Manhattan-távolságnak (Manhattan distance) is szokás nevezni. h2 szintén elfogadható heurisztikus függvény, mivel minden egyes mozgatással egy lapkát csak egy lépéssel lehet közelebb vinni a célhoz. A kiinduló állapotban az 1–8 lapkákra számított Manhattan-távolság:
h2 = 3 + 1 + 2 + 2 + 2 + 3 + 3 + 2 = 18
Ahogy reméltük, egyik sem becsüli túl a megoldás igazi költségét, ami 26.
A heurisztikus függvény minősítésének egyik lehetséges módja a b* effektív elágazási tényező (effective branching factor) megadása. Amennyiben az A* algoritmus által kifejtett összes csomópont száma egy adott problémára N, és a megoldás mélysége d, akkor b* annak a d mélységű kiegyensúlyozott fának az elágazási tényezőjével egyezik meg, amely N + 1 csomópontot tartalmazna. Ebből adódóan:
N + 1 = 1 + b* + (b*)2 + … + (b*)d
Például ha az A* algoritmus egy 5 mélységben fekvő megoldást 52 csomópont kifejtésével talál meg, akkor az effektív elágazási tényező 1,92. Az effektív elágazási tényező a problémaesetek függvényében változhat, megfelelően nehéz problémák esetén azonban általában nagyjából állandó. Így a b* kisszámú problémahalmazon végzett kísérleti mérése jó fogódzót adhat a heurisztikus függvény általánosságban vett használhatóságáról. Egy jól megtervezett heurisztikus függvény effektív elágazási tényezője 1 körüli érték, ami lehetővé teszi felettébb nagy problémák megoldását is.
A h1 és a h2 heurisztikus függvények teszteléséhez véletlenszerűen generáltunk 1200 problémapéldányt, 2–24 mélységű megoldással (100-100 példányt minden páros szám esetére), és megoldottuk azokat a h1 és a h2 heurisztikus függvényeket alkalmazva az A* fakereső algoritmussal, illetve a nem informált iteratívan mélyülő keresési algoritmussal is. A 4.8. ábra minden egyes stratégiára megadja az átlagosan kifejtett csomópontok számát és az effektív elágazási tényezőt. Az eredmények azt mutatják, hogy h2 jobb, mint h1, és hogy a nem informált keresés mindkettőnél sokkal rosszabb. A 14 hosszúságú megoldások esetén az A* h2-vel 30 000-szer hatékonyabb, mint a nem informált iteratívan mélyülő keresés.
ITERATÍVAN-MÉLYÜLŐ-KERESÉS és A* esetén h1 és h2 használatával. Az adatokat különböző hosszúságú megoldásokra a 8-as kirakójáték 100 egyedét megoldva átlagolva kaptuk.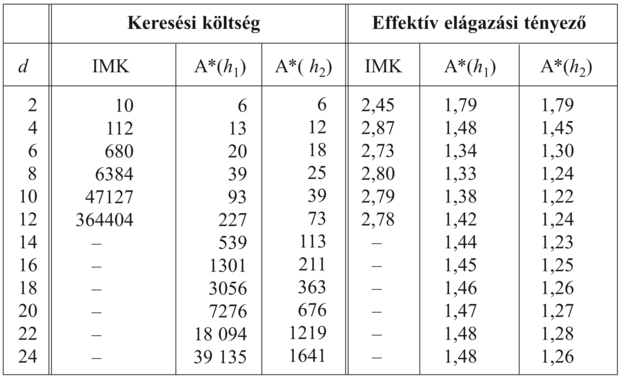
Feltehetjük magunknak a kérdést, hogy vajon a h2 mindig jobb-e, mint a h1? A válasz: igen. A két heurisztikus függvény definíciójából jól látszik, hogy minden n csomópontra h2(n) ≥ h1(n). Azt mondjuk, hogy h2 dominálja h1-et. A domináció közvetlenül átvihető a hatékonyságra: a h2-t használó A* algoritmus kevesebb csomópontot fog kifejteni, mint a h1-et használó (talán csak az f(n) = C* tulajdonságú néhány csomópontot kivéve). Ezt az alábbi egyszerű gondolatmenettel mutathatjuk meg. Idézzük fel a 4.1.2. szakasz - A* keresés: a teljes becsült útköltség minimalizálása részben tett észrevételünket, miszerint minden csomópont kifejtésre kerül, amelyre f(n) < C*. Ezzel egyenértékű az az állítás, mely szerint minden csomópont kifejtésre kerül, amelyre h(n) < C*– g(n). Mivel azonban h2 minden csomópontra legalább akkora, mint h1, így minden olyan csomópontot, amit kifejt a h2-t alkalmazó A* algoritmus, kifejti a h1-et alkalmazó A* algoritmus is, de h1 alkalmazása más csomópontok kifejtését is okozhatja. Ebből adódóan mindig jobb nagyobb értékeket adó heurisztikus függvényeket alkalmazni, amíg nem becsüljük túl a valódi költséget, és a heurisztika számítási ideje nem túlságosan nagy.
Láttuk, hogy mind h1 (a nem a helyükön lévő lapkák száma), mind pedig h2 (Manhattan-távolság) egész jó heurisztikus függvények a 8-as kirakójáték problémájához, és hogy h2 jobbnak bizonyult. De hogyan is állt elő a h2? Egy számítógép számára vajon lehetséges-e mechanikusan megalkotni ilyen heurisztikus függvényeket?
A h1 és h2 a 8-as kirakójátékban a fennmaradó út hosszát becsülik, azonban a játék egyszerűsített változatánál a tökéletesen pontos úthossz értékét adják meg. Ha a játék szabályait úgy módosítanánk, hogy egy lapka bárhová áthelyezhető legyen, nemcsak a szomszédos mezőkre, akkor h1 pontosan megadná a legrövidebb megoldáshoz vezető lépések számát. Hasonlóan, ha egy lapkát bármelyik szomszédos mezőre átmozgathatnánk, még akkor is, ha az adott mezőn már van egy másik lapka, akkor h2 megadná a legrövidebb megoldás pontos lépésszámát.
Fontos
Az olyan problémát, amelyben az operátorokra kevesebb megkötést teszünk, mint az eredeti problémában, relaxált problémának (relaxed problem) nevezzük. A relaxált probléma optimális megoldásának költsége egy elfogadható heurisztika az eredeti problémára. A heurisztika elfogadható, mert az eredeti probléma optimális megoldása definíciószerűen megoldása a relaxált problémának is, és így legalább olyan költséges, mint a relaxált probléma optimális megoldása. Mivel a számított heurisztika a relaxált problémára egy pontos költség, teljesítenie kell a háromszög egyenlőtlenséget, és ebből kifolyólag konzisztens 4.1.2. szakasz - A* keresés: a teljes becsült útköltség minimalizálása részben.
Amennyiben a probléma megfogalmazása formális nyelven adott, akkor a relaxált problémákat automatikusan is elő lehet állítani.[38] Például ha a 8-as kirakójáték operátorait az alábbi módon írjuk le:
Egy lapka az A mezőről a B mezőre mozgatható,
ha A és B szomszédosak, és a B mező üres
egy vagy több feltétel törlésével három relaxált problémát hozhatunk létre:
-
Egy lapka az A mezőről a B mezőre mozgatható, ha A és B szomszédosak.
-
Egy lapka az A mezőről a B mezőre mozgatható, ha a B mező üres.
-
Egy lapka az A mezőről a B mezőre mozgatható.
Az (a)-ból a h2 (Manhattan-távolság) vezethető le. A magyarázat az, hogy h2 helyes eredményt adna, ha minden lapkát sorra elmozgatnánk a saját célhelyére. A (b)-ből származtatott heurisztikával a 4.9. feladatban foglalkozunk. A (c)-ből a h1 (a nem a helyükön lévő lapkák száma) vezethető le, mert ez lenne a helyes eredmény, ha a lapkákat a célpozíciójukba egy lépésben el lehetne mozgatni. Vegyük észre, hogy lényeges, hogy e módszer által generált relaxált problémákat lényegében keresés nélkül meg lehet oldani, mert a relaxált szabályok a probléma 8 független részproblémává történő dekompozícióját teszik lehetővé. Ha a relaxált problémát nehéz megoldani, akkor a kapcsolatos heurisztikus értékek számítása drágának fog bizonyulni.[39]
Az ABSOLVER nevű program a „relaxált probléma” módszer és más egyéb módszer alkalmazásával (Prieditis, 1993), képes a probléma definíciójából automatikusan heurisztikus függvényeket generálni. Az ABSOLVER egy, az eddigieknél jobb heurisztikus függvényt hozott létre a 8-as kirakójáték megoldására, és ez a program találta meg az első használható heurisztikus függvényt a híres Rubik-kocka kirakásához.
Az új heurisztikus függvények előállításának egyik problémája, hogy felettébb nehéz felismerni a „nyilvánvalóan legjobb” heurisztikus függvényt. Ha egy problémához adottak a h1, ..., hm elfogadható heurisztikus függvények, és egyik sem dominálja a többit, melyiket kell választanunk? Mint az majd kiderül, nem kell választanunk. Az alábbi formulával a lehető legjobbat kaphatjuk meg:
h(n) = max{h1(n), ..., hm(n)}
Az így megkonstruált összetett heurisztikus függvény mindig azt a függvényt használja, amelyik az adott csomópontra a legpontosabb. Mivel az alkotóelemként felhasznált heurisztikus függvények mind elfogadhatók, ezért h is elfogadható. Ugyancsak könnyű bizonyítani, hogy h konzisztens. Továbbá h dominálja az összes, benne alkotóelemként felhasznált heurisztikus függvényt.
Elfogadható heurisztikus függvényeket származtathatunk az adott probléma részproblémájának (subproblem) megoldási költségéből is. A 4.9. ábra például a 4.7. ábrán látható 8-as kirakójáték egy részproblémáját mutatja. A részprobléma lényege az 1, 2, 3 és 4 lapkák helyükre való mozgatása. Világos, hogy e részprobléma optimális megoldásának költsége a teljes probléma megoldásának költségét alulról korlátozza. Bizonyos esetekben ez a függvény a Manhattan-távolságnál sokkal pontosabb.
A mintaadatbázisok (pattern databases) hátterében húzódó ötlet az, hogy tároljuk el az egyes részproblémaesetekhez tartozó pontos megoldási költségeket – ebben az esetben a négy lapka és az üres hely minden konfigurációjához (jegyezzük meg, hogy a másik négy lapka helye a részprobléma megoldása szempontjából közömbös, mozgásaik azonban a költségbe bele fognak számítani). A probléma teljes állapotához tartozó elfogadható hAB heurisztikus függvényt ezek után keresés közben úgy számítjuk ki, hogy a megfelelő részprobléma-konfigurációt az adatbázisból kikeressük. Maga az adatbázis úgy lett megtervezve, hogy a célállapottól visszafelé keresve minden új minta költségét feljegyeztük. Ennek a keresésnek a költsége a sok egymás után jövő problémaesetre kivetítve amortizálódik.
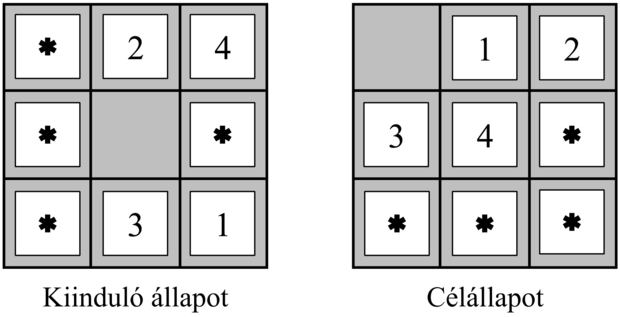
Az 1-2-3-4 lapka megválasztása nyilván tetszőleges, az adatbázist az 5-6-7-8 és a 2-4-6-8 stb. lapkákra is meg tudnánk konstruálni. Minden adatbázis egy elfogadható heurisztikát szolgáltat, és ahogy korábban elmagyaráztuk, ezen heurisztikákat kombinálni lehet, maximális értékükkel számolva. Egy ilyen típusú kombinált heurisztika a Manhattan-távolságnál sokkal pontosabb. A 15-ös kirakójáték véletlenszerűen generált egyedeire a kifejtett csomópontok számát egy 1000-es tényezővel lehet csökkenteni.
El lehetne tűnődni azon, hogy az 1-2-3-4 és az 5-6-7-8 adatbázisokból kinyert heurisztikus függvényeket nem lehetne-e összeadni, mivel úgy tűnik, a két részproblémában nincs fedés. A válasz nemleges, mert egy adott állapotban az 1-2-3-4 és az 5-6-7-8 részproblémák megoldásai majdnem biztosan osztoznak közös lépéseken – igen valószínűtlen, hogy az 1-2-3-4 lapkákat a helyükre el lehet mozdítani, anélkül hogy az 5-6-7-8-hoz ne nyúlnánk hozzá, és fordítva. És mi lenne, ha ezeket a lépéseket nem is számolnák be? Azaz nem az 1-2-3-4 részprobléma teljes költségével számolnánk, hanem csak az 1-2-3-4 lapka lépéseit vennénk figyelembe. Könnyű ilyenkor rájönni, hogy a két költség összege még mindig a teljes probléma megoldási költségének egy alsó korlátja. Ez a diszjunkt mintaadatbázis (disjoint pattern database) hátterében húzódó ötlet. Az ilyen adatbázisok használatával lehetségessé válik a 15-ös kirakójátékot milliszekundumok alatt megoldani, a Manhattan-távolsághoz képest a generált csomópontok száma egy 10 000-es tényezővel kisebb. A 24-es kirakójáték esetén kb. egymilliós gyorsítást lehet elérni.
A diszjunkt mintaadatbázisok jól működnek a csúszólapka-játékok esetén, mert a problémát úgy lehet felbontani, hogy egy-egy lépés csak egy részproblémára van hatással, hiszen egyszerre csak egy lapkát mozgatunk. A Rubik-kocka problémára ilyen bontást elvégezni nem lehet, mert minden mozgás 8, 9 vagy 26 kockát érint. Nem tudjuk egyelőre, hogy az ilyen problémák számára a diszjunkt mintaadatbázisokat hogyan lehetne definiálni.
A h(n) heurisztikus függvénytől elvárjuk, hogy az n csomópontbeli állapottól kezdve becsülje a megoldás költségét. Hogyan lenne képes egy ágens egy ilyen függvény megalkotására? Egy megoldást az előbbi részben adtunk meg – ami nevezetesen egy olyan relaxált problémának a kitalálása, amihez egy optimális megoldást könnyű találni. Egy másik megoldás a tapasztalatból való tanulás. A „tapasztalaton” itt azt értjük, hogy nagyon sok 8-as kirakójátékot kell megoldani. A 8-as játék minden optimális megoldása egy példát jelent, amiből h(n) tanulható. Minden példa egy, a megoldási úton elhelyezkedő állapotból és az onnan számított valós megoldási költségből áll. Ilyen példák alapján induktív tanulási algoritmus (inductive learning) segítségével egy olyan h(n) függvényt konstruálhatunk, amely (szerencsével) képes megjósolni a megoldás költségét a keresés során felbukkanó más állapotok esetén is. Ennek módszertanát, legyenek ezek neurális hálók, döntési fák vagy más módszerek, a 18. fejezet mutatja be (a 21. fejezetben leírt megerősítéses tanulás szintén alkalmazható).
Az induktív tanulási módszerek akkor működnek a legjobban, ha nem az állapot nyers leírását, hanem inkább az állapot kiértékeléséhez releváns jellemzőket (feature) kapják bemenetként. A „nem a helyén lévő lapkák száma” jellemző segítség lehet, ha az aktuális állapotnak a céltól vett távolságát szeretnénk megjósolni. Hívjuk ezt a jellemzőt x1(n)-nek. Vehetnénk a 8-as kirakójáték 100 véletlenszerűen generált konfigurációját, és gyűjthetnénk statisztikákat a megoldás aktuális költségéről. Esetleg azt találnánk, hogy ha x1(n) értéke 5, akkor a megoldás átlagos költsége 14 és így tovább. Ilyen adatok birtokában x1(n) értékéből jósolni lehetne h(n) értékét. Persze több jellemzőt is lehetne használni. Egy másik jellemző, x2(n) lehetne például „azon szomszédos lapkapárok száma, melyek a célállapotban is szomszédosak”. Hogyan lehetne x1(n)-et és x2(n)-et összekombinálni h(n) jóslása érdekében? Egy szokásos ötlet a lineáris kombináció használata:
h(n) = c1x1(n) + c2x2(n)
A c1 és c2 konstansokat módosítani lehet, hogy a megoldási költség aktuális adataira legjobban illeszkedjenek. Feltételezhetően c1-nek pozitívnak, c2-nek pedig negatívnak kellene lennie.
[38] A 8. és a 11. fejezetben erre a feladatra alkalmas formális nyelveket írunk le. Manipulálható formális leírásokkal a relaxált problémák konstruálása automatizálható. Egyelőre természetes nyelvet használunk.
[39] Vegyük észre, hogy a tökéletes heurisztikát könnyűszerrel megkaphatnánk, ha megengednénk h-nak a teljes szélességi keresés lefuttatását „stikában”. A heurisztikus függvény pontossága és számítási ideje között így kompromisszumot kell kötni.