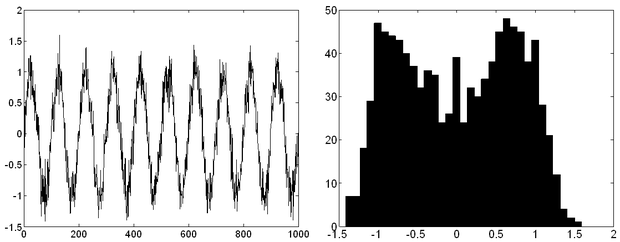
A jelfeldolgozás, szűrés területén legtöbbször abból indulunk ki, hogy a zajok Gauss eloszlásúak, ami végső soron gyakran az átlagolás típusú feldolgozási, zajcsökkentési eljárásokhoz vezet. (Megmutatható, hogy additív Gauss fehér zaj esetén a lineáris szűrési eljárások közül legkisebb négyzetes értelemben az átlagolás optimális eljárás.) Ugyanakkor a gyakorlati feladatmegoldás kapcsán gyakran találkozunk az úgynevezett kilógó adatok problémájával, a 13.3 pontban ezzel részletesebben is foglalkozunk majd. Ezek a kilógó adatok (outliers) nem modellezhetők jól Gauss zajként, és feldolgozásukat sokszor nem célszerű átlagolással megközelíteni.

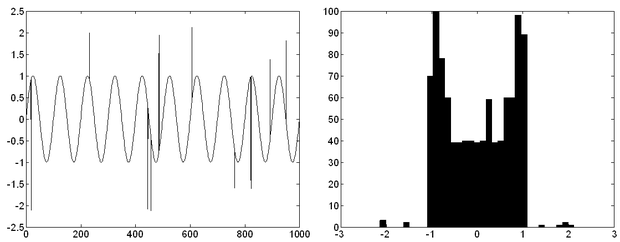
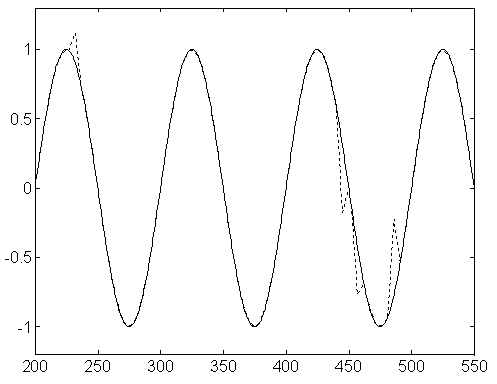
Az impulzuszajok kezelésére gyakran az átlagolásnál jobb eredményt ad az úgynevezett medián szűrés vagy annak valamely változata. A medián szűrés a rendezett statisztika szűrők (Order Statistic Filter, OSF) legismertebb alesete. Idősorok esetén az egy időablakba eső értékeket először sorbarendezzük, majd a sor középső elemét vesszük (természetesen a medián szűrés nemcsak idősoroknál, hanem sokféle mérési sorozatnál alkalmazható). Egyszerűen belátható, hogy ha az ablakhossz W=2L+1, akkor az L-nél nem szélesebb impulzusok sohasem jutnak el a rendezés során a középső pozícióba, így nem befolyásolják a kimenetet. A 13.2 ábrán látható idősor átlagolással javított változatának egy részletét láthatjuk a következő, 13.3 ábra ábrán.

Az átlagolás az impulzusszerű zajok amplitúdóját csökkentette ugyan, de időben "szétkente" a zajt, az eredetileg zajjal nem terhelt pontok is torzultak. (Ugyanis az impulzusok helyén megjelent az átlagoló szűrő impulzusválasz függvénye.) Ugyanezt a jelet ugyanakkora (jelen esetben 5 pont ablakszélességű) medián szűrővel javítva az eredeti jelet közel hibátlanul visszaállíthatjuk. (A medián szűrő olyan módon torzít, hogy levágja a jel csúcsait, 5 pontos szűrő esetén 2-2 pontot a csúcsnál. Ez a szinusznál igen kis torzítást eredményez, mert a csúcsnál lapos a függvény.) Természetesen, ha maga az alapjelünk is impulzusjellegű lenne - a zajhoz hasonló szélességű impulzusokkal - vagy rendelkezne ilyen szakaszokkal, akkor a medián szűrés nem lenne alkalmazható.

Nagyon lényeges tehát, hogy vegyük figyelembe a rendelkezésünkre álló (akár kvalitatív) információkat a jelről és a zajról, optimális vagy közel optimális eljárást csak a jel- és zajmodell figyelembevételével tudunk választani.

A tanításra használt adatokat torzító zaj hatásának csökkentésére több lehetőség is kínálkozik a tanítás során. Ezek közül az egyik, de nem az egyetlen, az előző pontban bemutatott zajszint csökkentés (a jel/zaj viszony javítása) valamilyen − legtöbbször lineáris − szűréssel, ami kétségtelenül a legismertebb és leginkább elterjedt módszer.

A problémának most egy ritkábban vizsgált aspektusát mutatjuk be, ahol a kiinduló kérdés, hogy milyen következményekkel jár, milyen megoldásokat tesz szükségessé, ha a zaj nemcsak a megfigyelt kimenet(ek)nél jelentkezik, amely a legtöbbször vizsgált eset, hanem a rendszer bemenetén/bemenetein is csak zajos megfigyelésre van lehetőségünk. A vizsgálatok során az derült ki, hogy a bemeneti zaj bizonyos értelemben nagyobb problémát jelent a modell kialakításnál, a tanításnál, mint a kimeneti. A szokásos feltételek mellett (nulla várható értékű Gauss zaj) a kimeneti zaj aszimptotikusan nem okoz torzítást az eredményben, ugyan lassítja a konvergenciát, számos problémát vet fel, de torzítatlan becsléshez juthatunk. Nem ez a helyzet, ha a bemeneten is megfigyelési zajjal kell küzdenünk, a becslés ilyenkor még a szokásos "kellemes tulajdonságú" (nulla várható értékű Gauss) zaj esetén is torzított becsléshez vezet. A kimeneti és bemeneti zaj tanulás során történő kezelését szolgálja az EIV (Errors In Variables) módszer, aminek ugyan számos problémája van, de a kérdés elvi jelentősége miatt mégis érdemes megismerkedni legalább az alapgondolatával [Dei86].

A zaj figyelembevétele − mint az előző pontban is kifejtettük − akkor történhet meg hatékonyan, ha rendelkezünk a zajra vonatkozó valamilyen ismerettel, pl. ismerjük az egyes tanítómintákat eltérő mértékben torzító zaj szintjét (szórását). Ez az ismeret valamilyen fizikai megfontolás alapján, esetleg a priori információkból nyerhető. Másik lehetőség − és a következőkben ezt mutatjuk be −, amikor a mérések alapján a jellel együtt a zajt is modellezni próbáljuk. Például úgy, hogy egy-egy szituációt többször is megpróbálunk előidézni, ugyanazt a helyzetet többször is megmérjük, és ebből nyerjük ki a különböző zajokra vonatkozó információkat. Természetesen ezt is akkor tudjuk hatékonyabban megtenni, ha legalább részleges, kvalitatív ismeretünk van a zajok jellegéről. Másrészt látni fogjuk, hogy a bonyolultabb modell (rendszer+zaj) felállítása több szabad paraméter meghatározását igényli, így több mérésre lehet szükségünk.

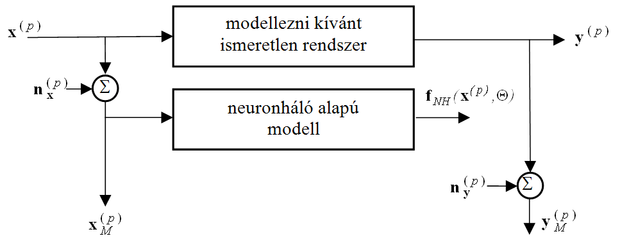
Tegyük fel, hogy az ismeretlen − neurális hálóval modellezni kívánt − rendszer bemenetét és kimenetét nem tudjuk zajmentesen megfigyelni (ld. 13.4 ábra). A valóságban mindig ez a helyzet, csak egyes esetekben elhanyagolhatóan kicsi lehet a megfigyelési zaj. Összesen P darab (p=1,2,...,P) { $x_M^{\text{(}p\text{)}}$ , $y_M^{\text{(}p\text{)}}$ } megfigyelt mintapár áll rendelkezésünkre a tanításhoz. A p-edik minta bemeneti jeleiből képzett vektort az összes komponensében egy-egy ${\sigma }_{x,p}$ szórású, nulla várhatóértékű Gauss eloszlású zaj terheli (ezt az ábrán $n_x^{\text{(}p\text{)}}$ zajvektor jelöli). A p-edik minta kimeneti jeleiből képzett vektort pedig az összes komponensében egy-egy ${\sigma }_{y,p}$ szórású, ugyancsak nulla várhatóértékű Gauss eloszlású zaj terheli (ezt az ábrán $n_y^{\text{(}p\text{)}}$ jelöli).

Az egyszerűbb leíró formalizmus érdekében azzal a − tulajdonképpen nem életszerű − feltevéssel éltünk, hogy egy-egy szituációban a bemeneti és kimeneti jelekből képzett vektorok összes komponensét azonos szórású zaj terheli (ezért lehet két skalárral, ${\sigma }_{x,p}$ -vel és ${\sigma }_{y,p}$ -vel jellemezni az adott mintát terhelő zajt). Ezt kézenfekvő módon továbbfejleszthetjük olyan módszerré, amelyben a komponens zajok is eltérő szintűek, de ennek hatására egy újabb index és újabb szumma jelenik meg az EIV megközelítésnél alkalmazott kritériumfüggvényben (ld. (13.1)). A gondolatmenet ugyanaz maradna, így az egyszerűség kedvéért a komponensenként azonos zajszintet feltételező eset bemutatását választottuk. Ugyanakkor viszont azt tesszük fel, hogy az egyes minták esetén a zaj különböző lehet (ezért indexeljük, az n zajokat p-vel), éppen ez ad esélyt a tanítás eredményeképpen előálló becslés javítására.

Ekkor az EIV módszer által javasolt lehetőség az, hogy a tanítás során használt kritériumfüggvényt a következőképpen módosítsuk:

$\begin{array}{c}\begin{array}{l}{C}_{EIV}=\frac{1}{P}{\displaystyle \sum _{p=1}^P\frac{{\left(y_M^{\left(p\right)}-f_{NH}\left(x^{\left(p\right)},\Theta \right)\right)}^T\left(y_M^{\left(p\right)}-f_{NH}\left(x^{\left(p\right)},\Theta \right)\right)}{{\sigma }_{y,p}^2}}+\\ \end{array}\\ +\frac{{\left(x_M^{\left(p\right)}-x^{\left(p\right)}\right)}^T\left(x_M^{\left(p\right)}-x^{\left(p\right)}\right)}{{\sigma }_{x,p}^2}\end{array}$ (13.1)

A kritériumfüggvényben két dolgot kell hangsúlyoznunk:

- az ismeretlen (megfigyelhetetlen) torzítatlan bemeneti értékek − az $x^{\text{(}p)}$ -k − is szerepelnek a kritériumfüggvényben, tulajdonképpen ezek olyan további szabad paraméterek, amelyeket az optimalizálásban a bemeneti zaj hatásának modellezésére használunk,

- az egyes mintákat torzító zaj szórásnégyzetével súlyozzuk a hibát, tehát a tudottan nagyobb zajjal terhelt minták kisebb súllyal kerülnek az optimalizálandó függvénybe.

Az optimalizálandó kritériumfügvényben a szummázott kifejezés első tagja tulajdonképpen a hagyományos LS (legkisebb négyzetes, least squares) hibakritériumnak felel meg annyi módosítással, hogy az egyes mintákhoz tartozó négyzetes hibaértékeket a kimeneti zaj szórásnégyzetének a reciprokával súlyozzuk. Tehát, ha tudjuk (a priori ismeretből, mérésből, bárhonnan), hogy az egyik minta zajosabb, mint a másik, akkor annak kisebb lesz a hatása a modell tanítás során történő kialakítására. A második tag a bemeneti mért és az − ismeretlen − tényleges mintavektorok eltérését igyekszik minimalizálni, ismét a mintához tartozó bemeneti zaj szórásnégyzetének a reciprokával súlyozva. Tulajdonképpen azt a járulékos feladatot viszi be a problémába, hogy "milyen lehetett a zajmentes, megfigyelhetetlen bemenet, a zajos értékek alapján becsülve?".

Az összehasonlítás kedvéért tekintsük át:

- A hagyományos LS módszernél az $x_M^{\text{(}p\text{)}}$ és $y_M^{\text{(}p\text{)}}$ adatok jelentik a konkrét optimalizálás (tanítás) szempontjából konstans értékeket, amelyek a konkrét feladatot jellemzik, a Θ paramétervektor pedig az optimalizálásban felhasználható változókat.

- Az EIV kritériumfüggvényében az $x_M^{\text{(}p\text{)}}$ és az $y_M^{\text{(}p\text{)}}$ adatok, valamint a ${\sigma }_{x,p}$ és a ${\sigma }_{y,p}$ szórásértékek jelentik a konkrét optimalizálás (tanítás) szempontjából konstans értékeket, a Θ paramétervektor és az ismeretlen zajmentes bemenetnek ( $x^{\left(p\right)}$ (p=1,2,...,P ) komponensei) pedig az optimalizálásban felhasználható változókat.

Ez az összehasonlítás már mutatja az EIV módszer egyik hátrányát is, nagyon megnő a szabad paraméterek száma, ezáltal az eljárás különösen hajlamossá válik a túltanulásra. A másik hátránya, hogy az eljárás bonyolultabb, mint az egyszerű LS modellalkotás. Előnye az eljárásnak ugyanakkor, hogy nem elhanyagolható bemeneti zajok kezelésére is képes [Van00].