A simasági feltételen túl számos további feltétel megfogalmazása alapul a priori információn [Lau06]. Ilyen feltétel lehet, hogy egy regressziós feladatnál a megoldás monotonitását előírjuk. A monoton LS-SVM regressziós megoldásra találunk példát [Pel04]-ben. A 6. fejezetben bemutatott LS-SVM optimalizálási problémához egydimenziós esetben még a következő feltétel megfogalmazása adódik:

$w^T\phi \left(x_i\right)\le w^T\phi \left(x_i{}_{+1}\right)\text{, ha }{x}_i<x_i{}_{+1}$ i=1,…,P-1, (12.1)

ahol x_i jelöli az SVM bemenetét, $w^T\phi \left(x_i\right)$ pedig a megfelelő választ. A járulékos információ a tanító eljárásba úgy épül be, hogy a Lagrange kritérium módosul:

$\begin{array}{l}L\text{(}w,b,e,\alpha ,\beta \text{)}=\frac{1}{2}{w}^{T}w+\frac{C}{2}{\displaystyle \sum _{i=1}^P{e}_{{}_i}^2}-{\displaystyle \sum _{i=1}^P{\alpha }_i\left\{w^T\phi (x_i)+b+e_i-d_i\right\}}\\ -{\displaystyle \sum _{\iota =1}^{P-1}{\beta }_i}\left\{w^T\phi \left(x_i{}_{+1}\right)-w^T\phi \left(x_i\right)\right\}\end{array}$ . (12.2)

Látható, hogy a szokásos Lagrange együtthatós tag mellett egy újabb tag jelent meg, amely szintén Lagrange multiplikátoros formában veszi figyelembe a monotonitásra vonatkozó feltételeket, ahol a ${\left\{{\beta }_i\right\}}_{i=1}^P$ együtthatók az új Lagrange multiplikátorok.

Más a priori ismeretet tükröző feltételek hasonló módon fogalmazhatók bele a tanuló eljárásba (a kiinduló kritériumfüggvénybe). Az eljárás hátránya, hogy minden újabb formálisan megfogalmazott a priori ismeret a teljes optimalizálási feladat származtatását igényli, ami egyes esetekben komoly matematikai nehézségekkel járhat. Az így kapott eljárások hatékonysága tehát jelentős mértékben függ attól, hogy milyen matematikai nehézségek merülnek fel az elsődleges, illetve a másodlagos optimalizálási feladatok megoldásánál. A monotonitást előíró feltételek figyelembevétele például kvadratikus optimalizálási feladatra vezet annak ellenére, hogy a standard LS-SVM-nél csak lineáris egyenletrendszert kell megoldanunk.

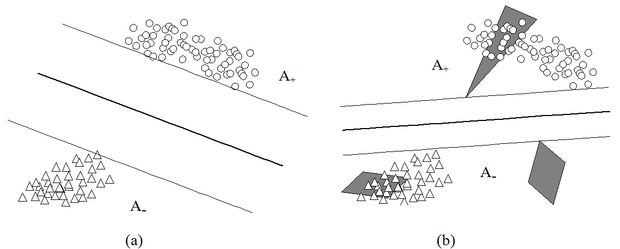
A tudásalapú szupport vektor gépeknél(knowledge-based support vector machines) az a priori tudás a bemeneti tér valamilyen korlátozott tartományára vonatkozik. Glenn Fung és munkatársai olyan osztályozós esetet vizsgáltak, amikor a bemeneti tér egyes poliéder tartományai teljes egészében az egyik osztályhoz tartoznak [Fun03]. Az osztályozási problémát ebben az esetben tehát egyrészt az ismert besorolású tanítópontok, másrészt a poliéder tartományok (egyenesekkel, síkokkal illetve hipersíkokkal határolt tartományok) specifikálják. A poliéder tartományoknak, mint a priori információnak az osztályozásra gyakorolt hatását illusztrálja a 12.1 ábra.

A Fung és Mangasarian által javasolt SVM-ben a megszokott négyzetes hiba helyett egyes normájú hiba szerepel a célfeltételben, így a feladat megoldása (hasonlóan az LS-SVM-hez) nem igényel kvadratikus programozást, elegendő a létrejövő lineáris egyenlőtlenségrendszert lineáris programozással megoldani. Az említett poliéder tartományok ezt a lineáris egyenletrendszert egészítik ki extra egyenlőtlenségekkel.

Hasonló eljárást dolgoztak ki függvényapproximációs feladatokra is, ahol az a priori információ a függvényre vonatkozóan extra korlátokat jelent [Man04]. Az alábbiakban bemutatjuk a lineáris kernel modellt, ami az alapfeladatot leírja.

Mint az eddigi függvényapproximációs feladatoknál most is egy $f:R^N\to R$ függvényt szeretnénk közelíteni az

$y\left(x\right)=w^{T}x+b$ . (12.3)

lineáris kapcsolattal az ${\left\{x_i,d_i\right\}}_{i=1}^P$ mintapontok felhasználásával. Jelölje a bemeneti mintavektorokat összefogó mátrixot

$X=\left[\begin{array}{c}{x}_1{}^T\\ x_2{}^T\\ ⋮\\ x_P{}^T\end{array}\right]$ . (12.4)

Ezzel a háló válasza az összes tanítópontra a következő formában is felírható:

$y=Xw+b1$ , (12.5)

ahol $1$ egy csupa egyesekből álló vektor. Feltételezve, hogy a háló válaszai közelítik a kívánt válaszokat, az approximáció hibája közel nulla, vagyis:

$Xw+b1-d\approx 0$ , (12.6)

ahol d a d_i, i=1,…,P kívánt válaszokból képezett vektor. Ahogy azt a kernel gépeknél már láttuk, a súlyvektor X sorainak lineáris kombinációjaként is előállítható:

$w=X^T\alpha$ . (12.7)

Itt $\alpha$ a lineáris kombináció együtthatóinak vektora. (A szokásos Lagrange multiplikátoros felírásnál $\alpha$ a Lagrange multiplikátorokból álló vektor.) Behelyettesítve a súlyvektor (12.7) kifejezését a (12.6) összefüggésbe, a lineáris kernel gépek szokásos formájú felírását kapjuk:

$K\left(X{X}^T\right)\alpha +b1-d\approx 0$ (12.8)

ahol $K\text{(}X,X^T\text{)}=X{X}^T$ a lineáris kernel mátrix. A hibát az $e\in R^P$ vektorral elemenként mérjük, és ennek a hibának az 1-es normáját minimalizáljuk, ahol az 1-es norma jelentése:

${\Vert x\Vert }_1={\displaystyle \sum _{i=1}^N\left|x_i\right|}$ (12.9)

Az 1-es norma alkalmazásának következménye, hogy a megoldást a szupport vektor gépeknél (6. fejezet) látott kvadratikus programozás helyett itt lineáris programozással megkaphatjuk. A megoldandó feladat a:

$J\left(\alpha ,b,e\right)={\Vert \alpha \Vert }_1+C{\Vert e\Vert }_1$ (12.10)

kritériumfüggvény minimumát biztosító α, b és e megtalálása, azzal a feltétellel, hogy teljesülnek az alábbi formában megfogalmazott egyenlőtlenségek:

$-e\le K\left(X,X^T\right)\alpha +b1-d\le e$ (12.11)

A feltételes optimalizálási feladat az alábbi lineáris programozási feladatra vezethető vissza:

$\begin{array}{c}\underset{\left(\alpha ,b,e,a\right)}{\text{min}}{1}^{T}a+C{1}^{T}e\\ -e\le K\left(X,X^T\right)\alpha +b1-d\le e,\\ -a\le \alpha \le a\end{array}$ (12.12)

Az eddigiek csupán azt illusztrálták, hogy egy kernel regressziós feladatnál a kritériumfüggvény a 6. fejezetben bemutatott kritériumfüggvényektől eltérő formában is megfogalmazható. A más megfogalmazást az indokolja, hogy így a kvadratikus programozási feladat helyett a megoldás lineáris programozással megkapható. A lineáris programozás számítási komplexitásban egyértelműen előnyösebb, mint a kvadratikus programozást igénylő „klasszikus” SVM.

A tudás alapú szupport vektor gépeknél járulékos információt is beépítünk az eljárásba. A fenti kiindulás mellett a lineáris egyenlőtlenségek formájában megfogalmazott a priori információ beépítése is lineáris programozási feladatra vezet. Az a priori információ itt azt jelenti, hogy a bemeneti tér egy poliéder tartományára további feltétel fogalmazható meg.

Ez a feltétel minden olyan $x\in R^N$ bemenetre vonatkozik, amely nem feltétlenül tartozik a tanítópontok közé, de melyre igaz, hogy egy

$Bx\le g$ , (12.13)

által meghatározott nem üres poliéderen belül található, ahol $B\in R^{L\times N}$ valamilyen együttható készlet, $g\in R^L$ pedig valamilyen valós számokból álló vektor. A feltétel azt fogalmazza meg, hogy a poliéder tartományra az approximálandó függvénynek dominálnia kell egy adott lineáris függvényt, vagyis a járulékos információ az alábbi implikáció formájában fogalmazható meg:

$Bx\le g\Rightarrow w^{T}x+b\ge h^{T}x+\beta$ , (12.14)

A lineáris függvény h és β paramétereit az a priori információ szolgáltatja. A súlyvektor (12.7) összefüggését felhasználva az implikáció

$Bx\le g\Rightarrow {\alpha }^{T}Xx+b\ge h^{T}x+\beta$ , (12.15)

formában is felírható. Ezt az implikációt kell még a (12.12) lineáris programozási feladathoz hozzávennünk.

Ennek érdekében az implikációt át kell alakítani lineáris egyenlőtlenségekké. Nem bizonyítjuk, de amennyiben a fenti implikációnak van megoldása, akkor az alábbi rendszer $u\in R^L$ megoldása ekvivalens az implikáció megoldásával:

$B^{T}u+X^T\alpha -h=0,-g^{T}u+b-\beta \ge \mathrm{0,}u\ge 0$ (12.16)

Az itt megfogalmazott feltételeket hozzávéve a (12.12)-ben megadott lineáris programozási feladathoz megkapjuk azt a lineáris programozási feladatot, mely a mintapontokon túl a járulékos ismeretet is figyelembe veszi. A minimalizálandó kritériumfüggvény, melynél a minimumot $\alpha ,b,e,a\text{és }u$ szerint keressük, ahol $u\ge 0$ , az alábbi:

$J\left(\alpha ,b,e,a,u\ge 0\right)=1^{T}a+C{1}^{T}e$ , (12.17)

a mellékfeltételek pedig:

$\begin{array}{c}-e\le K\left(X,X^T\right)\alpha +b1-g\le e,\\ -a\le \alpha \le a\\ -a\le B^{T}u+X^T\alpha -h\le a\\ -g^{T}u\ge \beta -b\end{array}$ (12.18)

A kapott megoldás meglehetősen speciális esetre érvényes, hiszen lineáris függvényapproximációs feladatból indultunk ki és az a priori információ is a bemenet lineáris függvényeként van megfogalmazva. Az eljárás nemlineáris esetre történő általánosítása viszonylag természetes módon megtörténhet. Ekkor egyrészt a lineáris kernel helyett nemlineáris kernellel dolgozunk, másrészt az a priori információt is mint a bemenet nemlineáris függvényét fogalmazzuk meg. Ennek részleteire azonban itt nem térünk ki.

A priori ismeretek beépítésére az eddig bemutatott eljárásokon kívül számos további eljárást is kidolgoztak. Ilyen eljárásokat ismertet pl. [Yu04], [Sun05] és [Le06], valamint az a priori információ beépítésének egy további lehetőségére ad példát a következőkben bemutatott súlyozott margójú SVM is.

A súlyozott margójú szupport vektor gépeknél(Weighted Margin Support Vector Machines, WMSVM) [Wu04] minden tanító mintához a rendelkezésre álló a priori információ alapján egy konfidencia értéket is rendelünk. A konfidencia értékek hatása, hogy az egyes tanító minták különböző súllyal vesznek részt az SVM tanításában. A súlyozott szupport vektor gép működését lineárisan szeparálható esetre mutatjuk be, de értelemszerűen az eredmények megfelelő kernelfüggvény-választást követően érvényesek a nemlineárisan szeparálható esetre is.

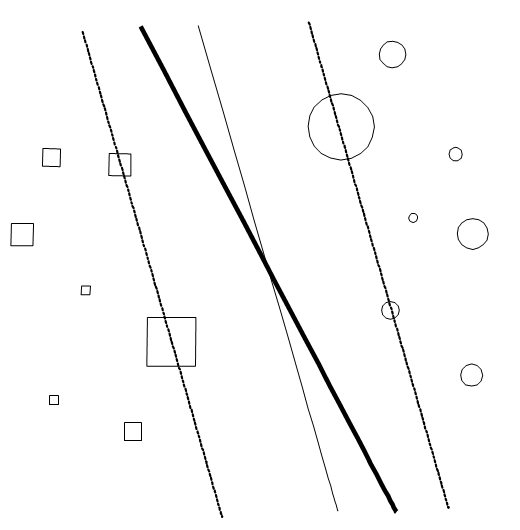
Adott egy lineárisan szeparálható tanítóhalmaz ${\left\{x_i,d_i\right\}}_{i=1}^P$ , és minden mintához rendelkezésünkre áll egy $v_i\in \left(\mathrm{0,1}\right]$ konfidenciaérték, ami a d_i kívánt válasz konfidenciaszintjét jellemzi. A konfidenciához olyan intuitív értelmezés adható, hogy minél nagyobb egy minta konfidenciája, annál nagyobb margót szeretnénk biztosítani az adott mintánál. A súlyozott SVM és a standard SVM közötti különbséget illusztrálja a 12.2 ábra. Az ábrán látható kétosztályos osztályozási feladatnál különböző méretű körök és négyzetek jelölik a két osztályba tartozó mintapontokat, és a körök, illetve a négyzetek mérete képviseli a mintaponthoz rendelt konfidenciát. Az ábrán vékony folytonos vonal jelzi az SVM szeparáló egyenesét. Látható, hogy ez nem veszi figyelembe a mintapontokhoz rendelt konfidenciát, míg a vastag vonal olyan elválasztó felületet képvisel, mely a nagyobb konfidenciájú pontoknál nagyobb távolságot (nagyobb margót), a kisebb konfidenciájú pontoknál pedig kisebb távolságot biztosít.

A súlyozott margójú megoldás származtatása a standard SVM 6. fejezetben bemutatott származtatásához hasonlóan történik. Itt is azt a w súlyvektorral és b eltolás értékkel jellemezhető hipersíkot keressük, ahol ${\Vert w\Vert }^2$ minimális, és ahol az osztályozásra vonatkozó

$f\left(v_i\right)d_i\left(w^T{x}_i+b\right)\ge \mathrm{1,}i=\mathrm{1,}\dots ,P$ (12.19)

feltételek teljesülnek. A (12.19) összefüggésben szereplő $f(\cdot )\in \left(\mathrm{0,1}\right]$ monoton csökkenő függvény biztosítja, hogy a „megbízhatóbb”, nagyobb konfidenciájú mintapontok nagyobb hatást gyakorolnak az elválasztó hipersíkra, ezeknél a pontoknál nagyobb margót kapunk.

A részletektől eltekintve a megoldás súlyvektorára a következő adódik:

$w^{\ast }={\displaystyle \sum _{i=1}^{P_s}{\alpha }_{{}_i}^{\ast }}{d}_{i}f\left(v_i\right)x_i$ (12.20)

ahol az ${\alpha }_{{}_i}^{\ast }\ge 0$ együtthatók most is a Lagrange multiplikátorok.

A standard SVM-hez hasonlóan itt is származtatható egy lágy margójú változat, ha egy gyengítő változót vezetünk be. Ekkor a megfelelő kritériumfüggvény a következő lesz

$J\text{(}w\text{)}=\frac{1}{2}{w}^{T}w+C{\displaystyle \sum _{i=1}^{P}g\left(v_i\right){\xi }_i}$ . (12.21)

Ennek w szerinti minimumát keressük azzal a feltétellel, hogy

$f\left(v_i\right)d_i\text{(}{w}^{\ast }{}^T{x}_i+b^{\ast }\text{)}\ge 1-{\xi }_{i}i=\text{1}\text{, 2}\text{, }\dots \text{,}P$ . (12.22)

ahol $f(\cdot )\in \left(\mathrm{0,1}\right]$ egy monoton csökkenő és $g(\cdot )\in \left(\mathrm{0,1}\right]$ egy monoton növekedő függvény és a ${\xi }_i\ge \mathrm{0,}i=\text{1}\text{, 2}\text{, }\dots \text{,}P$ értékek a gyengítő változó értékei. A szokásos lépések eredményeképpen itt is megkapjuk a megoldás súlyvektorát:

$w^{\ast }={\displaystyle \sum _{i=1}^{P_s}{\alpha }_i^{\ast }}{d}_{i}f\left(v_i\right)x_i$ , (12.23)

ahol teljesülnie kell még a következő összefüggéseknek:

$\begin{array}{ccc}{\displaystyle \sum _{i=1}^P{d}_i{\alpha }_{i}f\left(v_i\right)=\mathrm{0,}}& 0\le {\alpha }_i\le g\left(v_i\right)C\text{, }& i=\mathrm{1,}\mathrm{2,}\mathrm{....},P\end{array}$ . (12.24)