A már bemutatott utazó ügynök problémát a fentiek alapján könnyen lehet Boltzmann típusú neurális hálózatra implementálni. Először új bináris változókat vezetünk be a probléma leírására:

$u_{ip}=\{\begin{array}{l}\text{1 ha az út során az }i\text{-edik város a }p\text{-edik lépésben kerül meglátogatásra}\hfill \\ 0\text{ egyébként}\hfill \end{array}$

A bevezetett változókkal a feladat költségfüggvénye, az út hossza így írható le:

$C\left(P\right)={\displaystyle \sum _{i,j,p,q=0}^{n-1}{a}_{ijpq}{u}_{ip}{u}_{jq}}$ , (11.36)

ahol az $a_{ijpq}$ együtthatókat a távolságok alapján a következőképpen definiáljuk:

$a_{ijpq}=\{\begin{array}{l}{d}_{ij}\text{ ha }q\text{=(}p\text{+}1\text{)mod }n\hfill \\ 0\text{ egyébként}\hfill \end{array}$ (11.37)

A költségfüggvény minimalizálásán kívül ügyelni kell, hogy a megoldás valódi utat írjon le, ezért be kell tartani a következő két kényszert:

$\begin{array}{l}\forall p\text{-re }{\displaystyle \sum _{i\text{=0}}^{n-1}{u}_{ip}=\text{1}}\text{ (egy időpontban csak egy városban lehet az ügynök)}\text{,}\\ \forall i\text{-re }{\displaystyle \sum _{p\text{=0}}^{n-1}{u}_{ip}=\text{1}}\text{ (minden várost pontosan egyszer látogasson meg az ügynök)}\text{.}\end{array}$ (11.38)

A problémában szereplő minden bináris u_ip változónak a hálózat egy x_ip neuronja fog megfelelni, így a hálózat n² neuront fog tartalmazni. A Hopfield modellről szóló fejezetben leírtak alapján a hálózat súlyait az energiafüggvény megadásával definiáljuk. Az utazó ügynök probléma megoldásához definiált függvény három tagból áll, melyekből az első a költségfüggvény minimalizálásáért felelős, a másik kettő pedig a problémában szereplő két kényszert realizálja:

$E={\displaystyle \sum _{i,j,p,q=0}^{n-1}{a}_{ijpq}{x}_{ip}{x}_{jq}+c\left[{\displaystyle \sum _{i=0}^{n-1}{\left(1-{\displaystyle \sum _{p=0}^{n-1}{x}_{ip}}\right)}_{}^2+{\displaystyle \sum _{p=0}^{n-1}{\left(1-{\displaystyle \sum _{i=0}^{n-1}{x}_{ip}}\right)}_{}^2}}\right]}$ (11.39)

A hálózat súlyait az energiafüggvény tagjainak kiszorzása után közvetlenül megkapjuk, mivel nem szerepel benne x_ip négyzeténél magasabb hatványfokú tag. Könnyű belátni, hogy a függvény minimumpontjai ott vannak, ahol az út minimális és a megoldás megfelel mind a két kényszernek, ezenkívül teljesíti a függvénnyel kapcsolatban korábban leírt feltételeket.

Az eredmények azt mutatják, hogy az utolsó két tagot súlyozó c paramétert helyesen megválasztva igen jó megoldást talál a hálózat a problémára. Hozzá kell tenni azonban, hogy a tapasztalatok szerint a megoldás minősége jelentősen függ c értékétől.

11.8. ábra - Egy 4 várost tartalmazó utazó ügynök probléma.

Az ábrán látható 16 neuronból a 4 aktív (fekete) processzáló elem egy lehetséges megoldást mutat. Az ábrán jelöltük még az n₂₂ neuron súlyozott összeköttetéseit (a szaggatott vonalak a c súlyú kapcsolatokat jelölik).

A módszert hagyományos kombinatorikai algoritmusokkal összehasonlítva, a talált út hosszát vizsgálva a neurális hálózat a hagyományos algoritmusok megoldásainál valamivel gyengébb eredményt ad. Ennek alapvető oka, hogy a hálózat a véletlenszerű állapotból kiindulva részben olyan állapotokon keresztül jut el a stabil állapotig, amelyek nem valódi utaknak felelnek meg, míg a hagyományos eljárások közül a legjobbak csak ilyet vesznek figyelembe. Így a hálózat számára a problématér, melyben az optimális megoldást keresi, lényegesen nagyobb. Ennek a gondnak a kiküszöbölésére javasolták a hálózat struktúrájának olyan módosítását, hogy a neuronokat csoportba szervezve ún. "k-ból 1 neuron"-okat alakítottak ki, ahol garantált, hogy a hálózat minden neuron csoportjában mindig pontosan egy aktív van. Ilyenkor az energiafüggvény első tagjának módosítása után az utolsó két tag elhagyható. Ezzel a módszerrel a Boltzmann gépek mind minőség, mind sebesség tekintetében lényegesen jobb eredményeket értek el.

Hasonló problémára vezet a haditechnikában és a polgári távközlésben is felmerülő feladat, a nagyszámú rádiókapcsolatok létesítésének feladata. Igen bonyolult probléma több száz, esetleg néhány ezer rádiókapcsolathoz frekvenciát rendelni úgy, hogy azok ne zavarják egymást. A gyakorlatban a frekvencia értékeket a használt eszközöktől függő véges halmazból kell választani, és ki kell elégíteni a rádiókapcsolatok földrajzi elhelyezkedésétől függő kényszereket. Az alapproblémában a kapcsolatokhoz l₁,...,l_n frekvencia értékeket rendelünk az f₁,...,f_p lehetséges értékek közül. A kapcsolatokhoz rendelt frekvenciaértékekre a kényszerek a következő alakban írhatók fel:

$\left|l_i-l_j\right|\ge d_{ij}$ (11.40)

Minden lehetséges (l_i, f_k) kettőshöz rendeljünk hozzá egy bináris v_ik változót:

$\begin{array}{l}{v}_{ik}=1\text{ha }{l}_i=f_k\\ v_{ik}=0\text{ha }{l}_i\ne f_k\end{array}$ (11.41)

A v_ik változóknak feleltessük meg a neurális hálózat x_ik neuronjait, majd a neuronok közti kapcsolatok súlyait kell meghatározni. Itt is az energiafüggvény meghatározásával jutunk eredményre. A probléma költségfüggvénye legyen a ki nem elégített feltételek száma. Az ezt reprezentáló energiafüggvény tag a következő alakú:

$E_1={\displaystyle \sum _{i,p,j,q}\left(1-w_{ipjq}\right)x_{ip}{x}_{jq}}$ , (11.42)

ahol

$\begin{array}{l}{w}_{ipjq}=1\text{ha }\left|f_p-f_q\right|<d_{ij}\\ w_{ipjq}=0\text{egyébként}\end{array}$ (11.43)

Az energiafüggvényt, az utazó ügynök problémával bemutatottakhoz hasonlóan, ki kell még egészíteni egy taggal, amely minimumpontjában azt garantálja, hogy egy rádiókapcsolathoz pontosan egy frekvenciát rendelünk, illetve itt is alkalmazható a neuronok csoportba rendezésével (k-ból 1 neuronok) az utóbbi feltételt automatikusan teljesítő módszer.

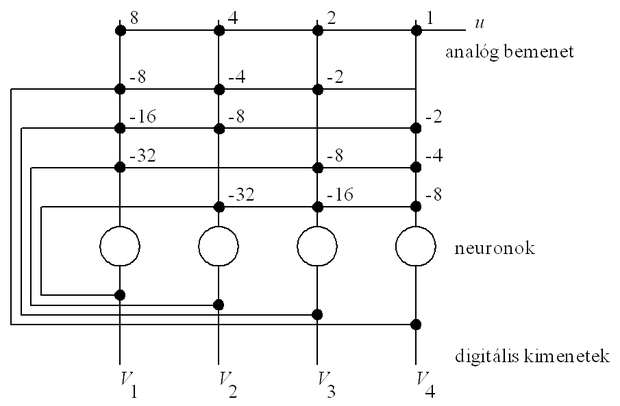
A/D konverterek érdekes megvalósítását mutatta be az alkalmazott hálózat névadója, John Hopfield. Mivel az eddigiekben csak kétértékű neuronokkal foglalkoztunk ezért itt a szerző által leírt folytonos értékű neuronokat alkalmazó A/D konverter megoldás digitális neurális hálózattal megvalósított változatát mutatjuk be [Hop86]. A hálózat modell itt kiegészül egy analóg bemenettel (a digitalizálandó jel − u), amelyet − hasonlóan a többi neuron kimenetének visszacsatolásához − súlyozott kapcsolatokon keresztül vezetünk a neuronok bemenetére. Az A/D átalakító költségfüggvénye legyen az átalakítás hibájának a négyzete, és a neuronok bináris kimenetei a digitalizált jel bitjei.

Így a hálózat energiafüggvénye:

$E={\left(u-{\displaystyle \sum _i{x}_i{2}_{}^i}\right)}_{}^2$ (11.44)

Ebből a hálózat súlyaira a következőket kapjuk:

w_ij=2^i+j (11.45)

Az analóg bemenetet súlyozó tagokra:

t_i=−2ⁱ (11.46)

Egy 4-bites A/D konverter látható a 11.9 ábrán. Bár a megoldás nem hódított teret más A/D megvalósítások mellett, jól mutatja, hogy a feladatok milyen széles köre értelmezhető optimalizációs problémaként és oldható meg Hopfield típusú hálózattal.

11.9. ábra - 4 bites A/D konverter megvalósítása Hopfield hálózattal

Feladatok

11.1 Tervezzen Hopfield neurális hálózatot, amely megoldja az N-királynő problémát. A logikai feladvány lényege, hogy egy N×N-es sakktáblán kell elhelyezni N királynőt úgy, hogy egyik se álljon másik által ütésben. Bizonyított, hogy minden N>3 esetre létezik megoldás. Határozza meg egy $N^2$ neuront tartalmazó hálózat súlyait úgy, hogy a hálózat minden neuronja a sakktábla egy-egy mezőjének felel meg és egy neuron a hálózat stabil állapotában akkor vesz fel aktív értéket, ha rajta egy királynő található.

11.2 Adja meg annak a Hopfield neurális hálózatnak az energiafüggvényét, amely képes megoldani a következő gráf partícionálási problémát. Válasszunk szét egy gráfot két egyenlő méretű részgráfra úgy, hogy a köztük található élek száma minimális legyen. A hálózat neuronjai reprezentálják a gráf csomópontjait úgy, hogy az energiafüggvény által meghatározott súlyokkal rendelkező hálózat stabil állapotában a neuronok aktív értéke jelölje az egyik, míg az inaktív érték a másik részgráfhoz való tartozást.

11.3 Mutassa meg, hogy az aszinkron Hopfield hálózatnak új hamis stabil állapotai jöhetnek létre, ha az önvisszacsatoló súlyok értékét növeljük.

11.4 Mutassa meg, hogy a szimmetrikus súlyokkal rendelkező szinkron Hopfield hálózatnál lehetséges, hogy két állapotváltozás után ugyanabba az állapotba kerül a hálózat (2 hosszúságú határciklus).