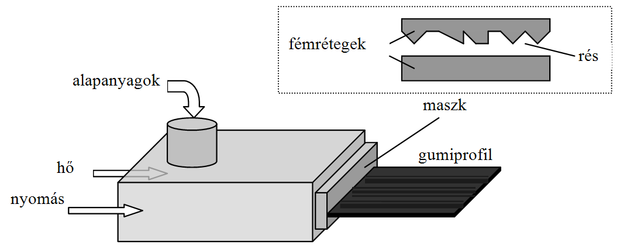
A gumigyártás modellezése is ilyen „kemény diónak” számít. A folyamat számunkra érdekes része úgy indul, hogy az alapanyagokat egy olvasztó-préselő gépbe (ún. extruder-be) öntik. Az extruder a gumikeveréket 110-140 °C fokon megolvasztja, majd a masszát 70-140 bar nyomással egy fémmaszkon préseli keresztül. Az extruder elhagyása után a gumikeverék megszilárdul, és közben deformálódik. Az deformáció a fémmaszk alakjának, valamint egyéb paramétereknek (pl. extruder típusa, hőmérséklet, keverék sűrűsége) a bonyolult, nemlineáris függvénye. A cél a fémmaszk megtervezése úgy, hogy a lehűlés és alakváltozás utáni gumiprofil minél közelebb legyen a kívánthoz.

Mivel az extruder-t elhagyó anyag végső, szilárd formája egy nehezen megjósolható alakváltozás során alakul ki, minden új termék gyártásának megkezdése előtt szükség van egy több iterációból álló kísérletezési szakaszra. Elkészítik a fémmaszkot, felhelyezik az extruder-re, végeznek vele egy próbagyártást, lemérik a kapott gumiprofilt, majd a mérés eredménye alapján pontosabb maszkot próbálnak készíteni. Egy ilyen iteráció költséges, ráadásul 4-5 napot is igénybe vehet, ezért egyáltalán nem mindegy, hogy hány maszkfinomítással sikerül elérni a kívánt pontosságot.

Az alkalmazottak, akik a kísérletezést végzik, teljesen hozzá vannak kötve ehhez a munkakörhöz (ami ráadásul unalmasnak számít). Mivel a „maszkfinomító” szakértelem csak lassan és elég heurisztikus módon szerezhető meg, ezen szakemberek betegsége vagy más céghez való távozása érzékenyen érintheti a gyárat.

Rendkívül hasznos lenne tehát, ha sikerülne kellően pontosan modellezni a megszilárdulás folyamatát. Még közvetlenebbül használható lenne egy inverz modell, amely megadja, hogy milyen fémmaszk paraméterek vezetnek a kívánt gumiprofil kialakulásához. Ha létezne ilyen, akkor a szakembereknek a kísérletezési fázis során rendelkezésre állna egy értékes támpontot adó szakértői vélemény. Itt merül fel a neurális hálózatok alkalmazásának ötlete, mivel a neurális hálózatok képesek modellezni olyan bonyolult, nemlineáris kapcsolatokat, amelyek nehezen írhatók le hagyományos eszközökkel.

Egy, a 90-es évek végén kifejlesztett neurális szakértői rendszerben radiális bázisfüggvényes (RBF) hálózattal próbálták megoldani a fent említett inverz modellezési feladatot [Pie99]. Az RBF hálózatok tanítására két „tiszta” megközelítés ismeretes. Az első megközelítés szerint a két réteg tanítása külön történik. A bázisfüggvény középpontokat és paramétereket egy klaszterező végeredménye alapján alakítják ki, majd a rejtett réteg súlyait rögzített bázisfüggvények mellett LMS algoritmussal tanítják. A második megközelítés szerint a hálózat összes paraméterét egyszerre tanítják, gradiens módszerrel. Az első megközelítés előnye a kis számításigény és a lokális minimumoktól való mentesség. Az egyszerűségért azonban pontosságcsökkenéssel fizethetünk. Ennek egyik oka, hogy a klaszterezés csak a tanítópontok pozícióját veszi figyelembe, így nem mintavételezi sűrűbben a közelítendő függvényt a gyors változás helyein. Az ismertetett rendszerben olyan megközelítést alkalmaztak, amely egyrészt szabályozási feladatokra van specializálva, másrészt próbálja ötvözni a két tiszta tanítási módszer előnyeit úgy, hogy közben a hátrányokból minél kevesebbet tart meg.

7.6. ábra - Az extruder működése, vázlatosan

Az alap RBF változatban a minimalizálandó mennyiség az átlagos négyzetes hiba. Szabályozási feladatok esetén viszont általában a maximális abszolút hiba minimalizálása a cél, ezért a szakértői rendszerben ezt használták kritériumfüggvényként. Egyébként azért választották ezt a hálózattípust, mivel RBF esetén a kritériumfüggvény ilyen irányú módosítása egyszerű és áttekinthető módon tehető meg.

A tanítást hálónövesztős módszerrel végezték, a következő módon: minden iterációban megkeresték, hogy melyik tanító pontnál volt a legnagyobb az abszolút hiba. Ha a hiba meghaladott egy küszöböt, akkor beillesztettek a hálóba egy új rejtett neuront úgy, hogy az új bázisfüggvény középpontja a maximális hiba helyére essen. Az új bázisfüggvény szélességparamétereit a szomszédos bázisfüggvények alapján állították be. Ezután meg lehetett határozni az új neuronhoz tartozó súlyt úgy, hogy az új bázisfüggvény középpontjánál a hiba nulla legyen (vagy újra lehetett tanítani az egész kimeneti réteget). (A megoldás – legalábbis céljait tekintve – hasonlít az 5. fejezetben ismertetett OLS eljárásra.)

Konkrét gyakorlati feladatunk esetén a cél a fémmaszk alakjának meghatározása magasságértékek [g₁, …, g_n] sorozataként az [r₁, …, r_n] kívánt gumiprofilból (ami szintén magasságértékek sorozata) és a gumikeverék sűrűségéből. Feltételezhetjük, hogy a keresztmetszet egy adott pozíciójánál létrejövő alakváltozásban csak a környező részeken található gumi magassága játszik szerepet. Ezért a g_i meghatározásához csak a szomszédos területekhez tartozó [r_i-k, …, r_i+k] gumiprofil értékeket érdemes felhasználni. (Valójában az extruder működéséből adódóan a rés mentén nem egyenletes a nyomás, ezért az alakváltozás az i abszolút pozíciótól is függ, de azt tapasztalták, hogy ez a hatás elhanyagolható.)

A kutatás eredménye félsiker volt. Az elért pontosság arra még nem alkalmas, hogy kiiktassa a kísérletezési fázist a terméktervezésnél, de a kapott neurális modell segítheti, felgyorsíthatja a szakemberek munkáját. Érdekes tapasztalat, hogy az általános helyzetű elliptikus bázisfüggvények alkalmazása ennél a feladatnál jelentős javulást hozott a körszimmetrikus bázisfüggvények használatához képest.

A Linz-Donawitz (LD) konverteres technológiával végzett acélgyártási folyamat neurális hálós modellezése is tipikus példája a neuronhálók ipari alkalmazásának. A konverteres acélgyártás az acélgyártási technológiák közül hatékonysága miatt az egyik legelterjedtebben alkalmazott eljárás. Az LD konverteres acélgyártás során egy nagy tartályban – ezt nevezik konverternek – történik a nyersvasból az acél készítése. Itt zajlanak le azok a fizikai és kémiai folyamatok, melynek során a kb. 4%-os széntartalmú, mintegy 1400 C°-os folyékony nyersvasból kb. 0,05% széntartalmú, mintegy 1670 C°-os acél készül, miközben a nyersvasban meglévő számos egyéb szennyezőanyag is kiég. Az eljárás hatékonysága abból ered, hogy a gyártási folyamathoz külső energiára nincs szükség, ugyanis a szén és a további szennyezőanyagok kiégetése hőtermelő folyamat. Így maga a kémiai folyamat biztosítja, hogy a véghőmérséklet magasabb lesz, mint a kiinduló hőmérséklet. Az eljárás legfontosabb fázisa az ún. fúvatás, amikor a konverterben lévő olvadékra nagytisztaságú oxigént fúvatnak. A gyártási folyamat során a megfelelő minőségű acél elérése érdekében a nyersvason kívül hulladékvas és számos adalékanyag felhasználása szükséges.

A gyártási folyamat főbb lépései a következők:

Az alapfeladat a betét megfelelő összeállítása és a fúvatási paraméterek, alapvetően a fúvatásnál felhasznált oxigén mennyiségének meghatározása. Minthogy a technológiából adódóan a gyártási folyamat közben mérések elvégzésére nincs lehetőség, az acél minőségét csak a fúvatás végén lehet megállapítani. A végtermék minőségét elsősorban a széntartalom és hőmérséklet jellemzi, tehát ez az a két minőségjellemző paraméter, melyeknek megfelelően szűk tartományon belül kell lenniük. A végtermék minőségét – ha adott betétből indulunk ki – elsődlegesen a fúvatási fázis lezajlása és ezen belül is a felhasznált oxigén mennyisége határozza meg. A megfelelő minőségű acél előállításának biztosításához tehát a felhasználandó oxigén mennyiségét kell meghatározni.

Bár a végtermék összetételét és hőmérsékletét mind a kiinduló betétösszetétellel, mind a fúvatással befolyásolhatjuk, a feladat komplexitása és számos nem, vagy nehezen kézbentartható jelenség miatt a betétösszeállítás és a fúvatási folyamat együttes optimalizálása nem járható út. Ezért a betét összeállítását adottnak vesszük (a valóságban általában ez a helyzet). A feladat tehát a betétösszeállítás többé-kevésbé pontos ismerete és a célul kitűzött kémiai összetétel és véghőmérséklet ismeretében a felhasználandó oxigén mennyiségének a meghatározása.

Az adagolandó oxigén minél pontosabb meghatározása alapvető gazdasági érdek. Ha a fúvatásvégi paraméterek nem megfelelőek (nem megfelelő hőmérsékletű és/vagy karbontartalmú az acél), a minőséget jellemző paraméterek csak jelentős idő- és költségigényes korrekciós műveletekkel módosíthatók.

7.7. ábra - Az előrejelzés, mint modellezési és inverz modellezési feladat.

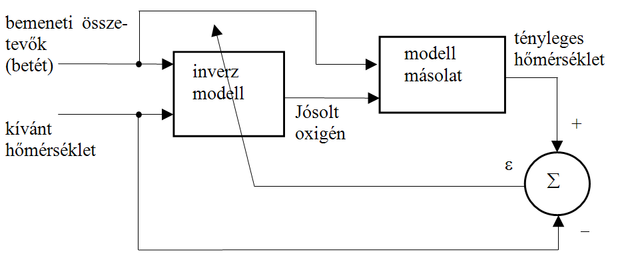
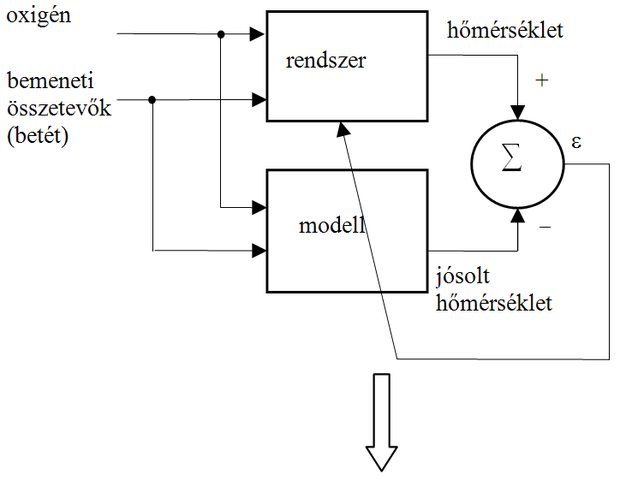
A megoldandó feladat ennek megfelelően egy olyan tanácsadó rendszer létrehozása, mely a rendelkezésre álló adatok (kiinduló betétösszetétel, a konverter állapotjellemzői és a célparaméterek: végkarbon és véghőmérséklet) alapján javaslatot ad a fúvatás során felhasználandó oxigén mennyiségére. Lényegében tehát folyamatvezérlési feladatot kell megoldani, melynek elengedhetetlen feltétele a kérdéses folyamat valamilyen modelljének felállítása. A modell a vizsgálandó folyamat bemenetei és kimenetei közötti kapcsolat minél pontosabb reprodukálását kell, hogy megvalósítsa. A modell ismeretében hozható létre a fúvatási oxigénre javaslatot tevő előrejelző, amely valójában a folyamat inverz modellje, mint ahogy ez az 7.7 ábrán látható [Hor99]. Az inverz modell kimenete állítja elő a folyamat vezérlőjelét (az ábrán a folyamat modelljének vezérlőjelét), ami az adott feladatban a javasolt oxigén mennyisége.

Egy folyamatmodell többféle megközelítésben is létrehozható. Lehet fizikai-kémiai modellt létrehozni, ahol a modell a rendszer felépítésének és működésének mechanizmusát is igyekszik minél pontosabban visszaadni, illetve készíthetünk viselkedési modellt, amikor csak az a cél, hogy a modell kívülről nézve minél inkább úgy viselkedjen, mint a modellezendő rendszer. Ilyenkor fekete doboz modellezésről beszélünk. Viselkedési vagy fekete doboz modell konstrukciójához bemeneti-kimeneti mintapontokra van szükségünk.

Fekete doboz modell létrehozását két fő szempont indokolhatja. Lehetséges, hogy a modellezendő rendszerről nem áll rendelkezésünkre annyi információ, ami fizikai-kémiai modell létrehozását lehetővé tenné, de az is lehet, hogy egy ilyen fizikai-kémiai modell létrehozása nagyságrendekkel bonyolultabb lenne, mint egy viselkedési modell felállítása. A konverteres acélgyártásnál valójában mindkét ok fennáll. Egyrészt a gyártási folyamat tényleges lezajlásáról nem szerezhető annyi információ, ami egy megfelelő pontosságú fizikai-kémiai modell létrehozását biztosítaná, másrészt, ha ilyen információ rendelkezésünkre is állna, akkor is túl komplex lenne a modellezési feladat. Ugyanakkor rendelkezésünkre állnak a gyártási folyamat során összegyűjtött bemeneti-kiemeneti mintapárok. Az adott probléma megoldásánál ezért a fekete doboz felállítása volt a cél, ahol a fő modellezési eszköz a neuronháló volt. (A neuronhálók rendszermodellezésre történő alkalmazásával a 8. fejezetben általánosabban is foglalkozunk.)

Mint a gyakorlati modellezési feladatok többségében, a probléma megoldásának egyik kulcskérdése a megfelelő adatbázis létrehozása és alkalmazása. Ez egyrészt azt jelenti, hogy a problémateret kellő mértékben le kell fednünk tanítópontokkal, másrészt azt, hogy ezen tanító pontok kellő "megbízhatóságúak" kell legyenek, továbbá, hogy az adatokat megfelelő módon kell reprezentálnunk. Az ipari környezetből adódóan az acélgyártási folyamat leírására egy meglehetősen nagy, ugyanakkor pontatlan, zajos és hiányos adatbázis áll rendelkezésre. Ennek megfelelően a munka lényegi részét képezte az adatbázis megfelelő kialakítása, ahol az alábbi problémákat kell megoldani (itt csak az adott alkalmazási feladatban felmerült speciális problémákat említjük meg, az adatbázis kialakítással kapcsolatos általános szempontokat – melyek jórészt ennek a munkának a kapcsán merültek fel – a 13. fejezetben tárgyaljuk):

Az adatbázis létrehozásának eredményeként egy kb. 4000 mintapontból álló adatkészlet állt elő (melynek kb. 60%-a tanításra, 40%-a tesztelésre volt felhasználva), mely 30-dimenziós bemeneti és kétdimenziós kimeneti adatokat tartalmazott. Ennek az adatkészletnek a felhasználásával történt a neurális modellek létrehozása és tesztelése. Az alkalmazásnál különböző méretű MLP-k kerültek felhasználásra. A legjobb eredményt két rejtett rétegű hálóval sikerült elérni, ahol az első rejtett rétegben 10, a másodikban 5 neuron volt.

A tesztkészleten történő kiértékelés szerint a neurális háló által javasolt oxigénmennyiség alapján az esetek mintegy 75-80%-ában a legyártott acél kimeneti paraméterei az előírt toleranciasávon belül voltak, ami az adott problémát tekintve igen jó eredmény. Meg kell azonban jegyezni, hogy a feladat komplexitása, a rendelkezésre álló viszonylag kisméretű mintakészlet és az adatok nagymértékű zajossága miatt, valamint abból adódóan, hogy ritkán speciális minőségű acél gyártására is szükség van, a feladat tisztán neurális hálózattal történő megoldása megfelelő minőségben nem lehetséges (a speciális minőségű gyártási esetekről nagyon kevés mintapont áll rendelkezésre, így ezen esetekre a neuronháló meglehetősen rossz eredményre képes csak). A ténylegesen kialakított modell ezért egy hibrid-neurális megközelítés eredményeként született, amely arra is képes, hogy a mintapontokon túl, más formában (pl. szabályok formájában) rendelkezésre álló információt is fel tudjon használni. A hibrid-neurális rendszerek kialakításának néhány fontos szempontjával a 12. fejezet foglalkozik, a konverteres acélgyártási folyamat hibrid-neurális modellezésének részletei pedig a megfelelő irodalmakban megtalálhatók: [Pat98], [Str98], [Hor99], [Pat00], [Ber01].

Az előbb ismertetett problémákon kívül az elmúlt években számos érdekes és/vagy gyakorlatilag fontos alkalmazás született. Az érdekes problémák között kell megemlíteni néhány olyan, a 80-as évek végén, 90-es évek elején készült alkalmazást, melyek célja inkább a figyelemfelkeltés, mint az igazi gyakorlati alkalmazás volt, bár természetesen az elkészült rendszerek gyakorlati feladatok megoldására is használhatók.

Az egyik első ilyen alkalmazás volt a NETtalk, amely egy angol szöveg-beszéd konverter [Sej87]. A hálót (MLP) egy olyan rendszerben alkalmazták, amely a bemenetére kerülő szöveget a rendszerben szintén meglévő beszéd szintézer segítségével alakította beszéddé. Ehhez az kellett, hogy a szöveg egyes karaktereihez olyan kódokat rendeljen egy neurális háló, mely kódok a beszédszintézer meghajtására alkalmasak. A teljes rendszer ezért két fő modulból áll: egy karakter-fonéma kód leképező neurális hálóból és egy hozzá kapcsolódó szintézerből. A megfelelő fonéma előállítása nem végezhető el környezetfüggetlen módon, ezért a karaktereket egymagukban nem dolgozhatja fel a neuronháló. A neuronháló bemenetére 7 egymást követő karakter bináris reprezentációja került, melyek közül a középsőnek megfelelő fonéma kód előállítása volt a neuronháló feladata. A leképezést egy 203 bemenetű 80 rejtett neuronnal felépülő 26 kimenetű hálónak tanították meg. Megemlítjük, hogy a NETtalk egy szabály alapú, hasonló célú és kereskedelmi forgalomban kapható rendszer, a DECtalk mintájára készült. A neurális megközelítés előnye a viszonylag rövid fejlesztési idő. A háló tanítása nagyságrendekkel rövidebb idő alatt megtörtént, mint a szabály alapú rendszer kifejlesztése.

Ugyancsak nevezetes alkalmazás az autonóm autóvezető rendszer (autonomous land vehicle in a neural network, ALVINN), melyet Carnegie-Mellon Egyetemen fejlesztettek ki, és amely egy gépkocsivezető cselekvése alapján tanít meg egy neurális hálót az autóvezetésre [Pom91]. A rendszer durva felbontású (30x32 képpontos) videoképet és a hozzá tartozó, sofőr által beállított kormánybeállítást kapott bemenetként. A feladatra 5 rejtett neuronú, 30 kimenetű MLP-t alkalmaztak. A 30 kimenet 30 lehetséges kormánybeállítást jelentett. A hálót vagy 1 a 30-ból kódolású kívánt válasszal tanították, vagy a kívánt választ olyan Gauss jelként fogalmazták meg, melynek maximális értéke a kívánt kormánybeállítást képviselő neuronhoz került. A feladat nehézségét a kellő számú tanító kép (mintapont) létrehozása jelentette. A megfelelő mennyiségű tanítómintához (összerendelt kép és kormánybeállítás) a valóságosan felvett képek transzformált változatait is felhasználták, sőt a tanítókészletet az egyes tanító ciklusok során részben cserélték is, hogy a háló ne alkalmazkodjon túlzottan egy adott tanítókészlethez. Közel 50 tanítási ciklus után, miközben a kocsit kb. 4 mérföld/óra sebességgel vezették a kijelölt úton, a háló nemcsak a megtanított környezetben, hanem attól eltérő úton, a tanítási körülményektől eltérő környezeti feltételek pl. más időjárási viszonyok között is képes volt a kocsi automatikus kormányozására mintegy 25 mérföld/óra max. sebességig.

A neurális hálózatok alkalmazása olyan esetekben is felmerül, amikor a szokásostól jelentősen eltérő, extrém körülmények miatt a jól bevált, hagyományos megoldás valamelyik infrastrukturális feltétele (pl. különböző mérőszenzorok megléte) nem, vagy csak nehezen biztosítható. Ez a helyzet például a kis teljesítményű (max. 15 kW-os) szélturbinák esetén, amelyeknek egyik fő alkalmazási területe a nehezen megközelíthető helyek árammal való ellátása.

Egy ilyen rendszer hatékony működtetéséhez a szélsebesség és a lapátvég-sebesség arányát (tip-speed ratio) lehetőleg konstans szinten kell tartani. Ez a generátorban található forgórész (ún. rotor) szögsebességének szabályozásával érhető el. A maximális energiakinyerést biztosító optimális szögsebesség a szélsebesség, és a pillanatnyilag leadott teljesítmény ismert függvénye. A hagyományos megközelítés szerint szélsebesség mérő szenzorokat helyeznének el a turbina környezetében, de ez az előbb említettek miatt költséges és nehezen karbantartható lenne.

A Floridai Egyetemen e helyett neurális megoldást fejlesztettek ki [Li05], amely szenzorok nélkül próbálja megbecsülni a szélsebességet a rotor szögsebességéből és a pillanatnyilag leadott teljesítményből. Konkrétan 2 bemenetű, 5 rejtett neuronnal rendelkező, 1 kimenetű MLP-t használtak A tanításhoz 10.000 mintahármast [szögsebesség, teljesítmény, szélsebesség] gyűjtöttek össze mérésekből. A neurális hálózat adaptivitását kihasználva a rendszert később olyan irányban is továbbfejlesztették, hogy képes legyen érzékelni, ha idővel megváltozik a maximális hatékonyságot biztosító tip-speed arány. A szélturbinát először szoftveres, majd hardwere-in-loop szimulátorban valósították meg. A teszteredmények azt mutatták, hogy a szélsebesség-becslős megoldás hatékonysága nem sokkal marad el a szenzorokkal elérhetőhöz képest. (Pl. az egyik kísérleti szélprofil maximumánál, egy 11 m/s-os széllökés közepén a rendszer 3.7 helyett 3.5 kW teljesítmény leadására volt képes.)

Szintén érdekes példa a neurális hálózatok szélsőséges körülmények között történő alkalmazására a Sao Paolo-i Egyetemen kifejlesztett tengeri olajkút monitorozó rendszer [Sim00]. Egy olajkút megfelelő üzemeltetéséhez rendszeresen mérni kell a hőmérsékletet és a nyomást a kút alján (ami néha jóval a tengerfenék alatt található). A problémát a mérési eredmények továbbítása jelenti. A hagyományos megközelítés szerint vezetékes átviteli közeget építenek ki a felszín és a kútfenék között, de ez a megoldás igen drága, és sérülékeny. A rádióhullámok ebben az esetben nehezen használhatók, mert a vízben rendkívül nagy az elnyelődés. Olcsó és robusztus alternatív megoldás az akusztikus adatátvitel használata, az acél olajszállító csövet használva átviteli közegként. A bináris adatok átvitele 2 különböző frekvencián történik, frekvenciamodulációs technika segítségével. A szokatlan átviteli közeg miatt persze számos probléma merül fel (pl. zaj, elnyelődés, ill. a csőelemek kapcsolódásánál többszörös visszaverődés, ill. nemlineáris torzulás), így a hagyományos demodulációs technikák nem alkalmazhatók. Az ismertetett megközelítés feladathoz igazított előfeldolgozást, és counterpropagation hálózatot [Hec89] használt^[3]. Az előfeldolgozás első része még nem feladat-specifikus: minden bit dekódolásánál meghatározzák a jelet tartalmazó időablakot, és mintavételezik a jelet. A neurális hálózatnál alkalmazott recepteket, stratégiákat neurális hálózat szimulátor program használatával fejlesztették ki, majd a legcélszerűbbnek bizonyult hálót C++-ban leprogramozták.

A rendszert laboratóriumban megépítették, és 100 méteres csővezetékkel tesztelték. A bemeneti jeleket szándékosan Gauss-zajjal torzították, hogy valamennyire felkészüljenek a laboratóriumitól eltérő, valós körülményekre. A vevő így a bitek 97,5 %-át dekódolta helyesen.

A neuronhálókat számos egyéb ipari probléma megoldásánál is alkalmazzák. Az előbbiekben említett acélipari alkalmazáson túl számos további acélipari alkalmazásra találunk példát. [Hao04] pl. egy nagykohó neurális, illetve hibrid-neurális modellezéséről számol be, míg [Zar00] az acélgyártásban alkalmazott hideghengerműben a hengerlési erő meghatározására szolgáló neurális megoldást ismertet. Egyéb alkalmazásokról szóló beszámolók a bőséges irodalomban találhatók.