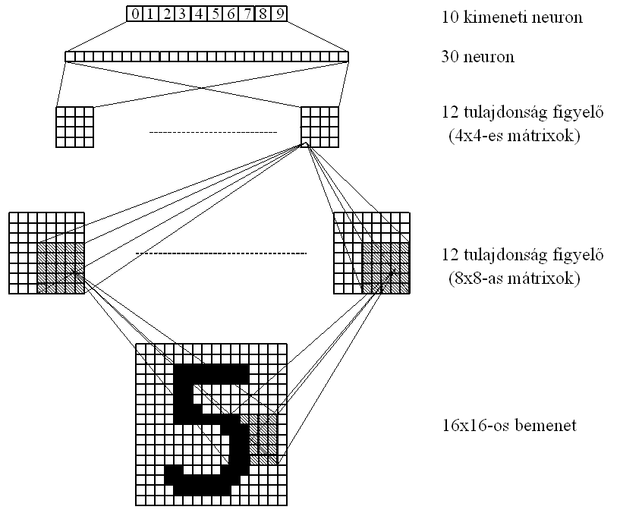
Az első alkalmazási megoldásban [LeC89] a többrétegű perceptron struktúra egy módosított változatát használták fel. A hálózat bemenetére közvetlenül a kézzel írt számjegy 16×16-os felbontású fekete-fehér pixel képe került. A bemenetek 3 rejtett rétegen keresztül kerültek a kimeneti réteg 10 elemére, amelyek rendre a 0-9 számjegyeknek feleltek meg.

Az első két rejtett réteg a bemeneti kép különböző részeiben felismerhető tulajdonságok felismeréséért felelős, míg az utolsó rejtett réteg és a kimeneti réteg neuronjai ezeknek az információknak a felhasználásával végzik az osztályozást.

7.1. ábra - Többrétegű perceptron struktúra karakterfelismerési feladathoz

Az első rejtett réteg 12 csoportból áll, ahol mindegyik csoport 64 neuront tartalmaz. A csoport minden műveletvégző egysége a bemeneti kép egy 5×5 pixelből álló négyzetével van összekötve úgy, hogy a szomszédos neuronokhoz a bemeneti kép két pixellel eltolt szomszédos részletei tartoznak. A csoportok mind a 64 neuronjának ugyanazok a súlyai, így ugyanazt a mintát detektálják a kép különböző részein. Így az első rejtett réteg minden neuronjának 25 bemeneti összeköttetése van. Ez a megoldás úgy biztosítja a kép egyes részeiben rejlő információ feldolgozását, hogy közben jelentősen csökkenti a tanítandó szabad paraméterek számát a teljes összeköttetéshez képest (majdnem 200 ezer kapcsolat helyett mindössze (25+64)12=1068, beleszámolva az összes neuronhoz tartozó független eltolás (bias) egységeket is).

A második rejtett réteg hasonlóan az elsőhöz egyes részletekben rejlő tulajdonságok felismerését végzi, és az ábrán látható módon az első réteg megfelelő 5×5-ös részmátrixaival van összeköttetésben. A harmadik réteg 30 neuront tartalmaz, amelyek teljes összeköttetésben állnak a második rejtett réteggel és a 10 kimeneti neuronnal. A hálózat összesen 1256 neuront és 9760 független súlyparamétert tartalmaz.

A hálózatot hibavisszaterjesztéses algoritmussal tanították, és a tanuláshoz 7000 számjegyet használtak fel. A tanított hálózat működését végül újabb 2000 számjegy felhasználásával ellenőrizték. A tanított mintahalmaz 99%-át ismerte fel helyesen a rendszer, míg a tesztelésre használt karaktereknél 95%-os eredményt értek el. Mivel az alkalmazás szempontjából előnyösebb, ha a számjegyek egy részénél a rendszer bizonytalanságot jelez, és ezzel csökkenthető a hibás felismerések száma (kisebb kárt jelent egy lassabban feldolgozott levél, mint egy rossz helyre továbbküldött), ezért azoknál az eseteknél, ahol több kimeneti neuron hasonló erősséggel jelezte, hogy a bemenet a hozzá tartozó osztályba való, ott a rendszer eredményét nem vették figyelembe. Így a hibás felismerések arányát sikerült 1% alá szorítani, miközben a levelek közel 10%-át a program kézi feldolgozásra irányította át.

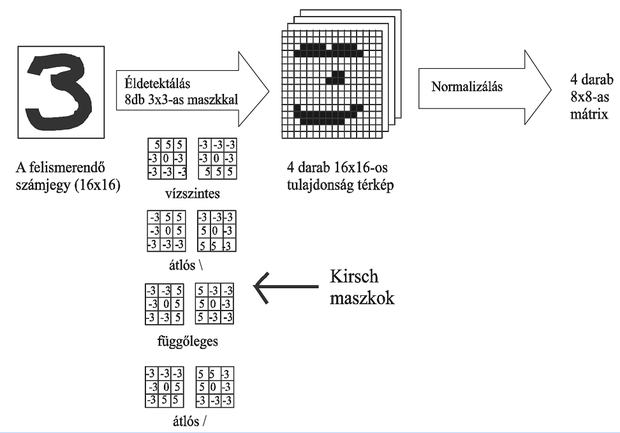
A második bemutatásra kerülő megoldás [Kne92] is a 16×16-os pixel képeket használta bemeneti adatként. Itt viszont az adatok nem kerültek közvetlenül a hálózat bemenetére, hanem egy előfeldolgozó egységen keresztül jutottak oda. A transzformáció alapgondolata az volt, hogy a számjegyek vonalszegmensekből állnak, és ezek előzetes felismerése megkönnyíti az osztályozást. Ezért a képen négy éldetektáló szűrést hajtottak végre az ún. Kirsch maszkokkal való végigpásztázással, aminek eredményeképpen négy képet kaptak, amelyeken az eredeti karakter vízszintes, függőleges illetve a két átló irányú vonalszegmensei vannak kiemelve. Ezt a 4 képet 8×8-as méretűre normalizálva alakították ki a hálózat 4×8×8=256 elemű bemenetét.

7.2. ábra - A kép előfeldolgozása

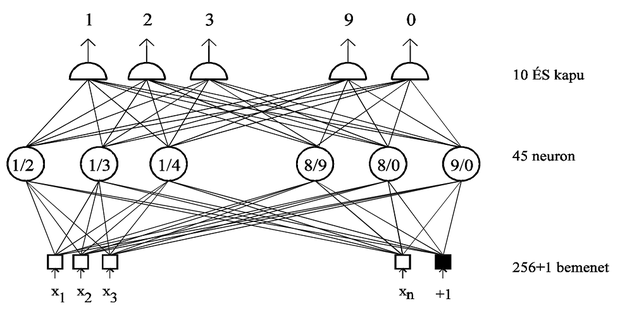
Az előfeldolgozott adat osztályozását egyrétegű perceptronnal oldották meg. Ennek a hálózatnak nagy előnye, hogy a többrétegű hálózathoz képest lényegesen gyorsabb a tanítása, viszont a megoldás létezésének feltétele az osztályok lineáris szeparálhatósága. Az egy hálózatra jutó feladat egyszerűsítése céljából (ami természetesen a hálózat teljesítményének a javulását eredményezi) és a lineáris szeparálhatóság esélyének növelése céljából az osztályozási feladatot szétbontották olyan részfeladatokká, ahol egy-egy hálózat csak két osztály között tesz különbséget. A 10 számjegy felismerését így 45 külön hálózat végezte, melyek mindegyike két osztályt különböztetett meg, rendre az 1/2, 1/3, 1/4, ... , 8/9, 8/0, 9/0 számjegyeket. Az osztályozás utolsó lépésében a megfelelő neuronok kimeneteit 10 darab ÉS kapura vezették, melyek kimenete jelezte az egyes számjegyek felismerését. (Ez a megoldás egy konkrét példája az olyan moduláris hálózat kialakításnak, ahol egy többosztályos osztályozási feladatot kétosztályos részfeladatokra bontunk fel, majd a részfeladatok megoldásaiból aggregáljuk a teljes megoldást. Az ilyen típusú feladat-dekomponálással általánosabban a 9. fejezetben foglalkozunk.)

Ennél a megoldásnál is felmerült, hogy szükséges a módszert úgy módosítani, hogy néhány karakter felismerésének visszautasítása árán a hibás osztályozások száma csökkenjen. Ezt itt úgy oldották meg, hogy a perceptronok döntési szintjét (küszöbét) megemelték, így a bizonytalan felismeréseket kiszűrték.

A hálózatok tanítását itt is gradiens módszerrel végezték, és ugyanazokat a karaktereket használták fel, mint az első megoldásnál. Az elért eredmények szinte teljesen megegyeztek az előző szakaszban bemutatott többrétegű perceptront alkalmazó megoldással, így a két módszer közötti választás a könnyebb implementálhatóság függvénye. Ebben az esetben ezt a kérdést csak a rendelkezésre álló eszközök és az időkorlátok ismeretében lehet eldönteni. Az elsőként bemutatott megoldás előnye, hogy egy lépésben, egy neurális hálózattal oldja meg a feladatot, és a tanított hálózat a felismerés során gyors működést tesz lehetővé. Hátránya viszont, hogy a tanulás folyamata időigényes. Ezzel szemben a második megoldás előnye, hogy egyszerűbb a rendszer és a tanítás lényegesen gyorsabb, viszont a felismerési folyamat során mindig szükség van a bemenő képek előfeldolgozására, ami időigényes.

7.3. ábra - Egyrétegű hálózat előfeldolgozott minták osztályozására

Bár itt a két megvalósítás lényegében egyforma eredményt hozott, a két módszer közti prioritás meghatározására általánosan is meg lehet fogalmazni bizonyos szempontokat. A többrétegű perceptron akkor működik jól, ha nagy mennyiségű, a lehetséges bemeneteket minél jobban reprezentáló tanító minta áll rendelkezésre. Ennek az az oka, hogy a tanítás során a hálózat nagyszámú szabad paraméterét kell beállítani. A másik megoldásnál az előzetes feldolgozás hatékonysága nem függ a mintáktól és az egyszerűbb hálózat beállításához nem szükséges a különösen nagy tanító mintahalmaz. Itt viszont határt szab a felismerő rendszer rugalmasságának az egyrétegű hálózat korlátozott általánosító képessége. Összefoglalva az első, általánosabb megközelítést akkor célszerű alkalmazni, ha a problémához kellő mennyiségű tanító példa áll rendelkezésre (az elégséges minta számát csak a feladat ismeretében lehet meghatározni), míg az előfeldolgozás és a kisebb hálózat használata akkor előnyösebb, ha viszonylag kevés minta áll rendelkezésre és a tanításra fordítható idő is rövidebb.

Az első megoldások megjelenése utáni években annyiféle különböző megközelítést próbáltak ki a számjegyfelismerési feladatra, hogy a probléma szinte klasszikussá vált. Bár a feladat alapvető megoldhatósága ma már nem kérdés, az egyre pontosabb és robusztusabb megoldások keresése jelenleg is nyitott terület. A tanuló algoritmusok kipróbálására, kísérletezésre is kitűnően alkalmas ez a gyakorlati színezetű, mégis kellően jól definiált probléma.

Most [Tak03] alapján egy ilyen, a többrétegű perceptron alkalmazásával megvalósult kísérlet eredményeit foglaljuk össze. Érdekes, hogy mennyire másként lehetett megközelíteni ugyanazt a feladatot az első megoldások megszületése után 10 évvel, összehasonlíthatatlanul fejlettebb számítástechnikai feltételek mellett.

Az 1990 körüli megoldásokban közös, hogy kis elemszámú mintakészleteket használtak, illetve a teljes összekötöttségű, „tiszta” MLP-hez képest erősen korlátozták a szabad paraméterek számát. Ennek egyik oka, hogy az akkor jellemző számítási teljesítmények mellett kivárhatatlanul hosszú ideig tartott volna egy 16×16 = 256 bemenetű MLP tanítása, mondjuk 500 rejtett neuronnal és fél milliós elemszámú tanító készlettel. 2002-ben már ki lehetett próbálni a nyers erő módszerét, vagyis egy hatalmas tanító készlet számjegyeit komoly előfeldolgozás nélkül rá lehetett adni egy nagy neuronszámú MLP bemenetére.

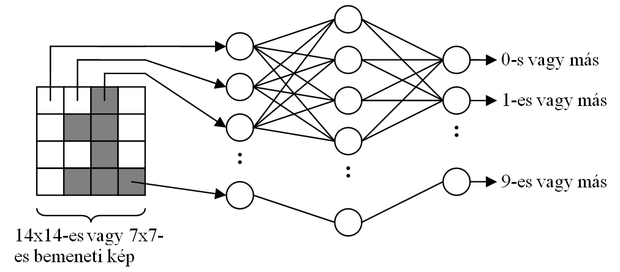
A kísérletben a hálózat a számjegyeket 14×14-es vagy 7×7-es felbontású változatban kapta, így 196 vagy 49 bemenettel rendelkezett. A rejtett rétegek számát illetve méretét változtatni lehetett, a kimeneti neuronok száma 10 volt (minden számjegyhez tartozott egy). Egy rejtett réteg esetén a hálózat felépítését a 7.4 ábra szemlélteti.

7.4. ábra - Számjegyfelismerés egy rejtett rétegű MLP-vel

Ez a felépítés tekinthető úgy is, hogy a rejtett réteg nemlineáris transzformációt hajt végre a bemeneten, a kimeneti neuronok pedig 10-féle lineáris szeparálást végeznek a transzformált térben. A tapasztalatok azt mutatták, hogy az egyes számjegyek szétválasztása az összes többitől nem oldható meg lineáris felülettel az eredeti térben. Ilyen helyzetekben merül fel lehetséges megoldásként a dimenziónövelő nemlineáris transzformáció alkalmazása, ami esetünkben azt jelenti, hogy a rejtett réteg nagyobb legyen a bemeneti rétegnél.

A számjegy-felismerési feladatra jellemző, hogy bizonyos típusú bemeneti torzítások kismértékű alkalmazása nem befolyásolja az osztályozás végeredményét. Ilyen például az eltolás, elforgatás, vagy vastagítás illetve vékonyítás. Ezt az a priori tudást sokféleképpen be lehet építeni a számjegyfelismerőbe. Talán a legegyszerűbb megközelítés a számjegyek torzított változatainak hozzávétele a tanító készlethez. 14×14-es vagy 7×7-es képekre a néhány pixellel való eltolás megvalósítható információveszteség nélkül (invertálható módon), ha a kép szélein található egy kis üres sáv. Forgatás vagy vastagítás esetén viszont a túl durva felbontású reprezentáció miatt a bemenet célzott módosítása mellett információveszteség is fellép. Ezért a kísérletben csak a számjegyek eltolt változataival bővítették a tanító készletet, amelynek elemszáma ily módon 60.000-ről 540.000-re volt növelhető (1 pixeles eltolást alkalmaztak függőlegesen, vízszintesen és átlósan).

Újabb döntési pont, hogy a bővítés memória vagy számítási erőforrás felhasználásával történjen-e. A kísérletben az utóbbi mellett döntöttek, vagyis csak a számjegyek eredeti változatát tárolták, és minden tanítási lépés előtt egy torzítási transzformációt hajtottak végre (amely esetleg helybenhagyás is lehetett).

A tanítást hagyományos backpropagation algoritmussal végezték, momentum módszer alkalmazásával. A tanítás paramétereinek beállítására tapasztalati úton, kísérletezéssel alakult ki a következő recept:

A tesztelést egy 10.000-es elemszámú mintakészlettel végezték, amely nem azonos a 10 évvel korábbi számjegyfelismerőknél használt készlettel. Szerencsére az új készlet bővebb és változatosabb a réginél, ezért feltételezhető, hogy az új tesztkészlettel elért eredmények nem romlanának a régi tesztkészletet használva.

7.5. ábra - Részlet a tesztelő készlet számjegyeiből

A tesztelő készlet érdekessége, hogy számjegyei más emberektől származnak, mint a tanító készlet számjegyei. A különböző beállítások mellett elért eredményeket az alábbi táblázat foglalja össze:

A táblázatból leolvasható, hogy a képek finomabb reprezentálása illetve a tanító készlet bővítése általában növelte a pontosságot, de nem mindig. Ebből is látszik, hogy az MLP hálózatok tanítása némileg heurisztikus folyamat, ahol jellemzően nem egyformán jól sikerülnek az egyes tanítási menetek. Érdemes kísérletezni, a tanítást többször megismételni, mert a tanulási ráta más stratégia szerint történő változtatása, vagy egyszerűen csak eltérő kezdeti súlyok használta esetleg egy kedvezőbb végállapot megtalálásához vezethet. Az elért maximális pontosság sokkal jobb, mint a 10 évvel korábbi eredmények. Érdekesség, hogy a kísérletben legpontosabbnak bizonyult MLP tanítása kb. 24 óráig tartott