6.1. Egy egyszerű kernel gép

A kernel reprezentációt a legegyszerűbben talán egy lineáris regressziósfeladat kapcsán mutathatjuk be. Adott egy lineáris be-kimeneti leképezést megvalósító eszköz, amit a továbbiakban lineáris gépnek nevezünk:

$y (x) = w^{T} x + b$ . (6.1)

Itt az eddigieknek megfelelően w a lineáris gép súlyvektora, b pedig az eltolásérték. Amennyiben rendelkezésünkre áll egy ${x_{i}, d_{i}}_{i = 1}^{P}$ tanítópont készlet, olyan súlyvektort keresünk, ami mellett a

$C (w) = \frac{1}{2} \sum_{i = 1}^{P} {(d_{i} - w^{T} x_{i} - b)}^{2}$ (6.2)

kritériumfüggvény minimumot vesz fel. A minimális négyzetes hibát biztosító súlyvektor − ahogy ezt az előző fejezetekben már láttuk − a kritériumfüggvény deriváltja alapján határozható meg. A b eltolásértéket a súlyvektor nulladik komponenseként kezelve és bevezetve a kibővített súlyvektort $\hat{w} = {[b, w^{T}]}^{T}$ , valamint a kibővített bemeneti vektort $\hat{x} = {[1, x^{T}]}^{T}$ is, a lineáris gép válasza $\hat{x}$ bemenet mellett

$y (\hat{x}) = {\hat{w}}^{T} \hat{x} = \sum_{i = 0}^{N} {\hat{w}}_{i} {\hat{x}}_{i}$ (6.3)

formába írható, ahol N a bemeneti x vektorok dimenziója. A tanítópontokban a lineáris gép válaszai és a kívánt válaszok közötti eltérésekből képezhetünk egy hibavektort

$ε (\hat{w}) = d - \hat{X} \hat{w}$ , (6.4)

melynek segítségével az eredő négyzetes hiba a

$C (\hat{w}) = \frac{1}{2} ε^{T} (\hat{w}) ε (\hat{w}) = \frac{1}{2} {(d - \hat{X} \hat{w})}^{T} (d - \hat{X} \hat{w})$ (6.5)

összefüggéssel adható meg. Itt d a tanítópontokban a kívánt válaszok vektora, $\hat{X}$ pedig a tanítópontok kibővített bemeneti vektoraiból képezett mátrix:

$\hat{X} = [\begin{matrix} {\hat{x}}_{1}^{T} \\ {\hat{x}}_{2}^{T} \\ ⋮ \\ {\hat{x}}_{P}^{T} \end{matrix}]$ . (6.6)

Elvégezve a gradiens számítást és a gradienst nullává téve

$\frac{\partial C (\hat{w})}{\partial \hat{w}} = - \hat{X} d + {\hat{X}}^{T} \hat{X} \hat{w} = 0$ (6.7)

a súlyvektor legkisebb négyzetes hibájú (LS) becslésétmost is a pszeudo-inverz segítségével kapjuk meg:

${\hat{w}}^{*} = {\hat{X}}^{T} {(\hat{X} {\hat{X}}^{T})}^{-1} d$ . (6.8)

Ha a kapott súlyvektort behelyettesítjük a (1.3) összefüggésbe, akkor adott $\hat{x}$ -re a lineáris gép válasza a következő lesz^[1]:

$y (\hat{x}) = {\hat{x}}^{T} {\hat{w}}^{*} = {\hat{x}}^{T} {\hat{X}}^{T} {(\hat{X} {\hat{X}}^{T})}^{-1} d$ . (6.9)

Vezessük be az

$α = {(\hat{X} {\hat{X}}^{T})}^{-1} d$ (6.10)

jelölést. Ekkor a kimenet az alábbi formában is felírható:

$y (\hat{x}) = {\hat{x}}^{T} {\hat{X}}^{T} α = \sum_{i = 1}^{P} α_{i} ({\hat{x}}^{T} {\hat{x}}_{_{i}}) = \sum_{i = 1}^{P} α_{i} K_{i} (\hat{x})$ . (6.11)

ahol α_i az $α$ vektor i-edik komponense és $K_{i} (\hat{x}) = {\hat{x}}^{T} {\hat{x}}_{i}$ . A (6.11) összefüggés származtatásánál figyelembe vettük a tanítópontokhoz tartozó bemeneti vektorok (6.6) összefüggését. Így ${\hat{x}}^{T} {\hat{X}}^{T}$ egy olyan vektor, melynek elemei az $\hat{x}$ bemenet és az ${\hat{x}}_{i}$ tanítópont-bemenetek skalár szorzataiként állnak elő:

${\hat{x}}^{T} {\hat{X}}^{T} = [{\hat{x}}^{T} {\hat{x}}_{1}, {\hat{x}}^{T} {\hat{x}}_{2}, \dots, {\hat{x}}^{T} {\hat{x}}_{i}, \dots, {\hat{x}}^{T} {\hat{x}}_{P}]$ (6.12)

A (6.11) összefüggés érdekessége, hogy a lineáris gép egy $\hat{x}$ bemenetre adott válasza a skalár szorzattal definiált $K_{i} (\hat{x}) = {\hat{x}}^{T} {\hat{x}}_{i}$ függvények súlyozott összegeként határozható meg. Egy lineáris gépnél ezeket a függvényeket nevezzük kernel függvényeknek vagy magfüggvényeknek.

A (6.11) összefüggés a lineáris regressziós leképezés alternatív felírását jelenti. Míg az eredeti (1.3) összefüggés a bemenetek súlyozott összegeként adja meg a választ, ahol a súlyokat a $\hat{w}$ súlyvektor képviseli, addig a kerneles reprezentációban a kimenet a $K_{i} (\hat{x}) = {\hat{x}}^{T} {\hat{x}}_{i}$ függvények súlyozott összegeként áll elő, ahol a súlyokat az α_i együtthatók jelentik.

A fenti (6.3) és (6.11) összefüggések ugyanannak a feladatnak két eltérő reprezentációját képviselik. Nyilvánvaló, hogy a két reprezentáció ekvivalens. A (6.3) összefüggés a megoldást a „bemeneti térben”, közvetlenül $\hat{x}$ függvényeként adja meg, míg a (6.11) összefüggés ugyanezt a „kernel térben”, a $K_{i} (\hat{x}) = {\hat{x}}^{T} {\hat{x}}_{i}$ kernel értékek függvényeként teszi meg.

A most vizsgált lineáris leképezésnél a kernel reprezentáció különösebb előnnyel nem jár, mindössze egy alternatív megadási formát jelent. A különbség a kétféle reprezentáció között csupán annyi, hogy a két szummás kifejezésben a tagok száma eltérő. A bemeneti térben történő összegzés N+1 tagból, míg a kernel térbeli P tagból áll. A kernel reprezentáció tehát akkor előnyös, ha a mintapontok száma, P jóval kisebb, mint a bemeneti adatok dimenziója, N.

Más a helyzet akkor, ha nemlineáris leképezést akarunk megvalósítani. A nemlineáris feladatok egy lehetséges megoldása a bázisfüggvényes hálók alkalmazása, vagyis, ha a kimenetet az (5.1) összefüggéssel megadott

$y (x) = \sum_{i = 0}^{M} w_{i} φ_{i} (x) = w^{T} φ (x)$ (6.13)

alakban állítjuk elő, ahol $w_{0}$ képviseli az eltolás tagot (bias), amennyiben $φ_{0} (x) \equiv 1$ .

A bázisfüggvényes leképezés a bemeneti térből az ún. jellemzőtérbe transzformál. A jellemzőtérbeli megoldás alternatívájaként viszont most is alkalmazható a kernel térre való áttérés. A lineáris esetre vonatkozó fenti gondolatmenetet követve a (6.13)-mal megadott leképezés kerneles változata úgy nyerhető, hogy a (6.11) összefüggésben minden $\hat{x}$ helyére $φ (x)$ kerül. (A továbbiakban – hacsak ez nem okoz értelmezési zavart – külön nem jelezzük, hogy kibővített bemeneti vektorról van szó.) Ezzel:

$y (x) = φ {(x)}^{T} Φ^{T} α = \sum_{i = 1}^{P} α_{i} (φ {(x)}^{T} φ (x_{i})) = \sum_{i = 1}^{P} α_{i} K_{i} (φ (x))$ , (6.14)

ami azt jelenti, hogy a kimenetet most is a skalár szorzattal definiált kernel értékek súlyozott összegeként állítjuk elő. Itt a

$φ {(x)}^{T} φ (x_{i}) = K_{i} (φ (x)) = K (x, x_{i})$ . (6.15)

függvény a kernel függvény, amit tehát a bázisfüggvények skalár szorzatával nyerhetünk, míg a

$Φ = [\begin{matrix} φ {(x_{1})}^{T} \\ φ {(x_{2})}^{T} \\ ⋮ \\ φ {(x_{P})}^{T} \end{matrix}]$ (6.16)

mátrix a tanítópontok jellemzőtérbeli reprezentációiból felépülő mátrix.

A (6.15) összefüggéssel megadott kernel reprezentáció itt is ekvivalens az eredeti reprezentációval ((6.13) összefüggés), és alkalmazása önmagában különösebb előnnyel itt sem jár az összegzésben szereplő tagok esetleges kisebb számán túl. A kernel reprezentáció előnyei akkor látszanak, ha a kernel függvényeket nem a bázisfüggvények skalár szorzataként határozzuk meg, hanem közvetlenül felvesszük, tehát ha nem a bázisfüggvényekből, hanem a kernel függvényből indulunk ki. Kernel függvényként azonban bármilyen függvény nem használható, hiszen a kernel függvény még akkor is bázisfüggvények skalár szorzatával származtatható függvény kell legyen, ha a származtatásnál nem ezt az utat választjuk. Érvényes kernel függvénynek bizonyos feltételeket teljesítenie kell. A kernel függvény megválasztása implicit módon meghatározza a jellemzőtérre való leképezést biztosító bázisfüggvényeket is. Ez viszont már magában rejti a kernel megközelítés egy nagyon lényeges előnyét.

Amint az a (6.14) összefüggésből látszik a kerneles reprezentáció a tanítópontoknak megfelelő számú (P) kernel függvény-érték súlyozott összegeként áll elő, függetlenül attól, hogy az implicit módon definiált jellemzőtér dimenziója (M) mekkora. A kernel függvény megválasztásától függően a jellemzőtér dimenziója nagyon nagy, akár végtelen is lehet, ami a (6.13) szerinti kimenet előállítást nagyon megnehezítené, sőt akár lehetetlenné is tenné, miközben a kernel reprezentáció komplexitása a tanítópontok száma által mindenképpen korlátozott. Minthogy a kernel térbeli megoldás ekvivalens a jellemzőtérbeli megoldással, a kernel módszerekkel azt tudjuk elérni, hogy a megoldás komplexitását akkor is korlátozni tudjuk, ha egyébként a megfelelő jellemzőtérbeli megoldás extrém módon komplex lenne. A kernel függvények bevezetésének ezt a hatását kernel trükknek (kernel trick) nevezzük.

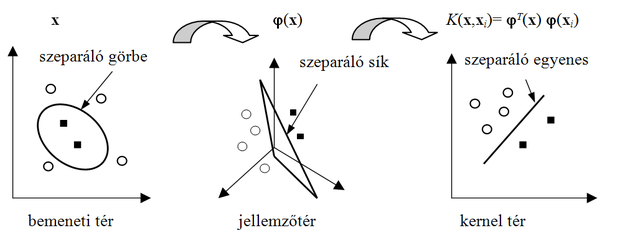
Nemlineáris esetben a kernel reprezentációt – legalábbis koncepcionálisan – két lépésben érjük el. Először a bemeneti térről megfelelő bázisfüggvények alkalmazásával nemlineáris dimenziónövelő transzformációt hajtunk végre. Ennek eredménye a jellemzőtérbeli reprezentáció. A feladatot azonban nem itt, hanem egy újabb transzformáció után a kernel térben oldjuk meg. A jellemzőtér és a kernel tér között a skalár szorzat teremti meg a kapcsolatot, és mindkét származtatott reprezentációra igaz, hogy az eredetileg nemlineáris probléma a származtatott reprezentációkban már lineárisan megoldható. A reprezentációk kapcsolatát mutatja a 6.1 ábra.

A koncepcionális származtatás mellett azonban fontos hangsúlyozni, hogy a kernel reprezentáció alkalmazásánál nem a 6.1 ábrán bemutatott utat követjük, a kernel térbe nem a jellemzőtéren keresztül jutunk el, hanem épp ellenkezőleg a kernel térből indulunk ki, és ez automatikusan definiálja a jellemzőteret. A fordított út előnye – ami a kernel trükk következménye –, hogy nem kell a jellemzőteret definiálnunk, ami egyébként sok esetben komoly nehézséget jelentene, dolgoznunk sem kell a praktikusan nehezen kezelhető jellemzőtérben, hanem közvetlenül a kernel teret definiáljuk és a megoldást is itt nyerjük. Mindehhez az egyik legfontosabb követelmény a megfelelő kernel függvény megválasztása.

6.1. ábra - A nemlineáris leképezések az eredeti probléma tértől a kernel térig.

^[1] A válasz (6.9) szerinti meghatározásához az ${(\hat{X} {\hat{X}}^{T})}^{-1}$ inverznek léteznie kell. Ha $(\hat{X} {\hat{X}}^{T})$ szinguláris vagy közel szinguláris, a regularizáció alkalmazható, amikor ${(\hat{X} {\hat{X}}^{T})}^{-1}$ helyett ${(\hat{X} {\hat{X}}^{T} + λ I)}^{-1}$ szerepel. (ld. még 2.1 szakasz illetve Függelék.)

Mesterséges Intelligencia Elektronikus Almanach

Elsődleges linkek

6.1. Egy egyszerű kernel gép