A tanítóval történő tanításnála tanítandó rendszer változtatása összetartozó be- és kimeneti tanító mintapárok felhasználásával történik. Ilyenkor a tanuló eljárás célja az, hogy a tanítandó rendszer felépítését (struktúráját és/vagy paramétereit) olyan módon válasszuk meg vagy alakítsuk ki, hogy a megtanított rendszer − amely valamely vizsgált rendszer modelljeként jelenik meg − működése minél inkább feleljen meg a vizsgált rendszer működésének. Úgy is fogalmazhatunk, hogy modell-illesztési feladatot kell megoldanunk.

A modell-illesztés feladata minden olyan esetben megjelenik, amikor "identifikálni", egyszerűbben kifejezve "meghatározni", "azonosítani", "mérni" szeretnénk valamit, vagy amikor "követni" szeretnénk folyamatokat. De lényegében ugyanerről van szó akkor is, amikor bonyolult, nehezen kezelhető jelenségekhez egyszerűbb − könnyebben kezelhető −, ugyanakkor főbb vonásaiban mégis hasonlóan viselkedő "modelleket" hozunk létre, illetőleg amikor a klasszikus regresszió-számítás módszerét alkalmazzuk.

A modell-illesztési feladat általánosan a következő formában fogalmazható meg: Adott egy rendszer, mely a bemenetei és a kimenetei között valamilyen $g(.)$ leképezést valósít meg. A leképezés nem ismert, viszont rendelkezésünkre áll egy ${\left\{z_i\right\}}_{i=1}^l={\left\{x_i,d_i\right\}}_{i=1}^l$ mintapont-készlet, melynél az összetartozó bemeneti és kimeneti értékek közötti kapcsolatot az ismeretlen leképezés adja meg. A mintakészlet elemei, a mintapontok általában többdimenziós vektorok, melyek a mintatérben helyezkednek el.

A tanulási feladat az, hogy egy $f\left(x,w\right)$ paraméteres függvényhalmazból, − ahol $w\in W$ a függvényhalmaz paramétere és W a paramétertér − válasszunk egy függvényt olyan módon, hogy adott $x_i$ bemenetre a kiválasztott függvény $y_i=f\left(x_i,w\right)$ válasza valamilyen értelemben a lehető legjobban közelítse az ismeretlen leképezés azonos bemenetre adott d_i válaszát. A d_i válaszokat kívánt válaszoknak (desired response) nevezzük. A függvényhalmaz szabad paramétereit tartalmazó w vektort a W paramétertér megfelelő pontjaként a rendelkezésre álló mintapontok alapján kell megválasztani vagy meghatározni.

Az ${\left\{x_i,d_i\right\}}_{i=1}^l$ mintapont-készletet tanító készletnek vagy tanító mintakészletnek (training set) nevezzük, azt az eljárást pedig, melynek során a tanító mintakészlet felhasználásával az $f\left(x,w\right)$ leképezést kialakítjuk, tanulásnak (learning). A tanuló eljárás célja tehát egy valamilyen értelemben optimális w* paraméter meghatározása a tanító mintakészlet alapján.

Amennyiben az $f\left(x,w\right)$ leképezést egy neuronháló valósítja meg, a függvénykészlet megválasztása a neuronháló típusának és architektúrájának megválasztásával történik, míg a tanítás valójában a w paramétervektor meghatározását, becslését szolgálja. Ebben az értelemben a tanulás egy paraméterbecslési eljárás. Nyilvánvaló tehát, hogy a tanuló eljárások és a statisztikai becslések között szoros kapcsolat található. Erről a kapcsolatról részletesebben a 2.4 alfejezetben szólunk.

Osztályozás és regresszió

Az általános modell-illesztési feladatosztályon belül több feladatcsoportot különböztethetünk meg. Ezek közül a neuronhálókhoz kapcsolódóan az osztályozási és a regressziós feladatcsoportokkal foglalkozunk.

Az osztályozási feladatoknál a rendszer által képviselt leképezést az

$\left(x_1,d_1\right),\left(x_2,d_2\right),\mathrm{...},\left(x_l,d_l\right)\in R^N\times \left\{\pm 1\right\}$ (2.1)

tanító mintapontok alapján kell közelítenünk, míg a regressziós feladatnál a rendelkezésre álló összerendelt tanító mintapárok:

$\left(x_1,d_1\right),\left(x_2,d_2\right),\mathrm{...},\left(x_l,d_l\right)\in R^N\times R$ (2.2)

egy, általában zajos leképezés $d_i=g\left(x_i\right)+n_i$ eredményeképpen nyerhetők. Itt $g(.)$ egy determinisztikus függvény, a regressziós függvény, $n_i$ pedig a kimeneti megfigyelési zaj. A (2.1) összefüggés kétosztályos osztályozási feladatot tételez fel, de nyilvánvalóan tetszőleges (véges) számú osztályra is kiterjeszthető. A különbség mindössze annyi, hogy a válasz nemcsak két érték közül kerülhet ki, hanem a véges számú lehetséges értékek közül bármelyik lehet. A (2.2) által definiált mintapontokról feltételeztük, hogy egy több-bemenetű − egykimenetű leképezésből származnak. Az egydimenziós kimenet feltételezése nem korlátozza a feladat általános megfogalmazását. A többdimenziós kimenetre való kiterjesztés természetes módon lehetséges.

A megfigyelési zajról általában feltételezzük, hogy várható értéke bármely x mellett nulla, továbbá, hogy a megfigyelési zaj és a regressziós függvény korrelálatlanok egymással, vagyis

$E_{n|x}\left\{n|x\right\}=0$ , (2.3)

illetve

$E\left\{ng\left(x\right)\right\}=0$ . (2.4)

Nulla várható értékű, korrelálatlan zaj mellett a regressziós feladat valójában egy feltételes várhatóérték-képzési feladat, vagyis $g\left(x\right)$ a megfigyelés feltételes várhatóértéke

$g\left(x\right)=E_{d|x}\left\{d|x\right\}$ . (2.5)

Minősítés, hibamértékek

A legjobb approximációt biztosító függvény meghatározásához az approximáció minőségét jellemző mértékre van szükség. Ez a mérték egy hibafüggvény (error function) felhasználásával határozható meg, amit költségfüggvénynek (cost function) vagy veszteségfüggvénynek (loss function) is szokás nevezni. A veszteségfüggvény − amit a továbbiakban $L\left(d,f\left(x,w\right)\right)$ -vel fogunk jelölni − mind a háló válaszának, $f\left(x,w\right)$ -nek, mind a rendelkezésre álló $d\left(x\right)$ kívánt válasznak a függvénye: leggyakrabban az approximáció $\epsilon \left(x,w\right)$ hibájának a függvénye, ahol a hibát a kívánt válasz és a tényleges válasz különbségeként definiálhatjuk:

$\epsilon \left(x,w\right)=d\left(x\right)-f\left(x,w\right)$ . (2.6)

A tanuló rendszer konstrukciója – akár osztályozási, akár regressziós probléma megoldására irányul – véges számú tanító mintapont alapján történik. A tanuló eljárás célja azonban általában nem az, hogy a véges számú tanítópontban kapjunk megfelelő válaszokat, hanem egy olyan leképezés megtanulása, amely a tanítópontok által reprezentált bemenet-kimenet kapcsolatot is megadja. A tanuló rendszer tehát általánosítóképességgel (generalization capability) kell rendelkezzen: olyan esetekben is „jó” választ kell adjon, mely esetek nem szerepelnek a tanítópontok között. A tanulás nehézségét épp ez adja: véges számú tanítópont alapján kell egy problémáról „általános tudást” szerezni.

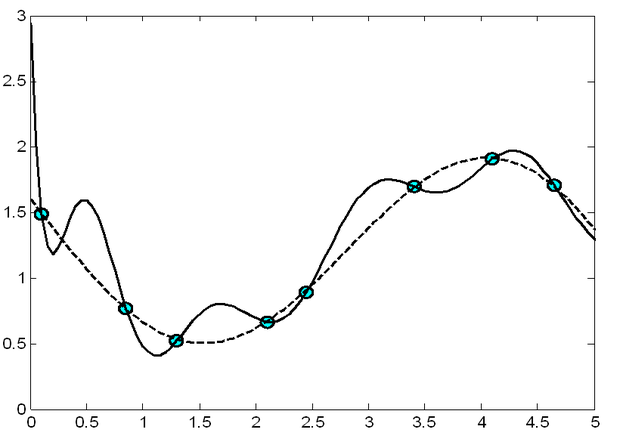
Az adatokból történő tanulás egy rosszul definiált feladat. Példaképp nézzünk egy függvényapproximációs problémát. Mint a 2.1. ábrán látható, a pontokkal jelölt tanítópontokra több – akár végtelen sok – különböző függvény illeszthető, melyek mindegyikére igaz lehet, hogy átmegy a megadott pontokon, vagy azokat tetszőleges pontossággal közelíti, miközben a tanítópontoktól eltérő pontokban az egyes függvények viselkedése nagymértékben különbözhet.

A tanuló rendszer minősítésére ezért olyan mértékre van szükségünk, amely nem csupán azt mondja meg, hogy a tanuló rendszer a tanító mintapontokat milyen pontosan tanulta meg, hanem a rendszer általánosítóképességéről is mond valamit.

A veszteségfüggvény adott bemenet mellett minősíti a tanuló rendszert. A minősítésre azonban alkalmasabb mérték, ha a veszteség összes pontra vonatkozó átlagos értékét, a veszteség várható értékét, az ún. kockázatot (risk) határozzuk meg, ahol a kockázat a veszteségfüggvényhez rendelt számérték:

$R\left(w\right)=E_{x,d}\left\{L\left(d,f\left(x,w\right)\right)\right\}$ . (2.7)

A kockázat meghatározásánál a várható értéket a minták $p\left(x,d\right)$ együttes sűrűségfüggvénye szerint kell vennünk. Ugyanakkor − ahogy ezt az R(w) jelölés mutatja is − a kockázat a paramétervektor függvénye, amit szokás kritériumfüggvénynek (criterion function) is nevezni és C(w)-vel jelölni. A továbbiakban a két elnevezést és a kétfajta jelölést egymás alternatívájaként kezeljük: adott szövegkörnyezetben azt a jelölést/elnevezést használjuk, melyet az aktuális témakörben általánosabban használnak.

Osztályozási feladatoknál veszteségfüggvényként általában az osztályozási hibát használhatjuk, vagyis

$L\left(d,f\left(x,w\right)\right)=\{\begin{array}{c}0\text{ha}d=f\left(x,w\right)\\ 1\text{ha }d\ne f\left(x,w\right)\end{array}$ (2.8)

Ekkor a (2.7) szerinti kockázat a téves osztályozás valószínűségét adja meg. A tanulás tehát olyan $f\left(x,w^{\ast }\right)$ osztályozó konstrukcióját célozza, amely a hibás osztályozás valószínűségét minimalizálja. Itt w* az adott függvényosztályt és a rendelkezésre álló tanító mintapont-készletet tekintve az optimális paramétervektor.

A regressziós feladatoknál az egyik leggyakoribb veszteségfüggvény a hiba négyzetes függvénye:

$L\left(d,f\left(x,w\right)\right)={\left(d\left(x\right)-f\left(x,w\right)\right)}^2$ , (2.9)

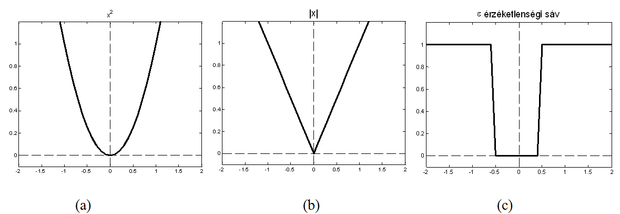
bár más veszteségfüggvények alkalmazása is szokásos. Ilyen függvény lehet pl. az abszolútérték függvény vagy ennek kissé módosított változata az ún. ε érzéketlenségi sávval rendelkező abszolútérték függvény. Egyes speciális alkalmazásokban szerepet kaphatnak a különböző abszolútérték-hatvány függvények, és ezek lineáris kombinációi, az "igen-nem" függvény, amely az optimumnál, ill. annak egy rögzített, általában szűk környezetében nulla, egyébként egységnyi (vagy más pozitív) értéket vesz fel. Speciális alkalmazásokban használnak logaritmikus, trigonometrikus, hiperbolikus függvényekből alkalmasan előállított hibafüggvényeketis. Egyes osztályozási feladatoknál előnyösen alkalmazható az

$L\left(d,f\left(x,w\right)\right)=-\left(d\text{ln}f\left(x,w\right)+\left(1-d\right)\text{ln}\left(1-f\left(x,w\right)\right)\right)$ (2.10)

keresztentrópia függvény is. (A téma iránt mélyebben érdeklődők az irodalomban pl. [Cic93] találhatnak ilyeneket, pl. a logisztikus, a Huber, a Talvar és a Hampel függvényt.)

A hibafüggvény konkrét alakja − bizonyos közös lényeges tulajdonságokon (pl. az optimumhoz tartozó szélsőérték) túlmenően − a feladat jellegétől, az a priori ismeretektől (pl. különböző zaj eloszlások esetén más-más függvény biztosítja a "jobb" viselkedést), és bizonyos mértékig szubjektív tényezőktől is függ. A hibafüggvény megválasztása befolyásolja a tanuló eljárás jellemzőit: az eljárás konvergenciáját, illetve a konvergencia sebességét, sőt magát a megoldást is. Néhány fontosabb hibafüggvényt a 2.2 ábrán mutatunk be.

A kockázat négyzetes veszteségfüggvény mellett a tanuló rendszer átlagos négyzetes hibája. Az átlagos négyzetes hiba vizsgálata több hasznos következtetésre ad lehetőséget. Ennek érdekében bontsuk fel a kockázat kifejezését több tagra:

$\begin{array}{l}R\left(w\right)=E\left\{{\left(d-f\left(x,w\right)\right)}^2\right\}=E\left\{{\left(d-g\left(x\right)+g\left(x\right)-f\left(x,w\right)\right)}^2\right\}\\ =E\left\{{\left(d-g\left(x\right)\right)}^2\right\}+E\left\{{\left(f\left(x,w\right)-g\left(x\right)\right)}^2\right\}+2E\left\{\left(d-g\left(x\right)\right)\left(g\left(x\right)-f\left(x,w\right)\right)\right\}\end{array}$ (2.11)

Feltételezve, hogy − amint azt az előbbiekben kikötöttük − a megfigyelési zaj nulla várható értékű, továbbá, hogy a zaj és a $g\left(x\right)$ leképezés korrelálatlan, a (2.11) összefüggés utolsó tagja zérus, hiszen $d-g\left(x\right)=n$ . Így a kockázat az alábbi két tagra bontható:

$R\left(w\right)=E\left\{{\left(d-g\left(x\right)\right)}^2\right\}+E\left\{{\left(f\left(x,w\right)-g\left(x\right)\right)}^2\right\}=E\left\{n^2\right\}+E\left\{{\left(f\left(x,w\right)-g\left(x\right)\right)}^2\right\}$ (2.12)

Az első tag nem függ a tanuló rendszer leképezésétől, csupán a megfigyelt kívánt válasz és a $g\left(x\right)$ ideális leképezés eltérésétől, ami épp a megfigyelési zaj. Az első tag tehát a megfigyelési zaj varianciájával egyenlő. Ez a hibakomponens nyilvánvalóan független a tanuló eljárástól, és nem is csökkenthető w megfelelő megválasztásával: az optimális w meghatározásánál tehát figyelmen kívül hagyható. Ebből következik, hogy a kockázat minimumát biztosító w* paramétervektor egyben a tanuló rendszer és a regressziós függvény válaszainak átlagos négyzetes eltérését is minimalizálja.

A feltételezett zajmodell mellett tehát a zajos megfigyelések ellenére a kockázatminimalizálás a regressziós függvény átlagos négyzetes értelemben vett legjobb közelítését eredményezi. Másfelől, ha a tanulás célját úgy fogalmazzuk meg, hogy azt az $f\left(x,w\right)$ -t keressük, amely adott x mellett a lehető legjobban közelíti a megfelelő $d$ kívánt választ, akkor a megoldást az

$MSE\left(w\right)=E\left\{\left(f\left(x,w\right)-g\left(x\right)\right){}^2\right\}$ (2.13)

minimalizálása biztosítja. A válasz helyességének természetes mértéke tehát a tanuló rendszer leképezése és a regressziós függvény kimenete közötti eltérés átlagos négyzetes értéke (MSE).

Az approximációs hiba (2.13) kifejezése alkalmas a megoldás minősítésének további elemzésére is. Az átlagos négyzetes eltérés ugyanis tovább dekomponálható, és ennek a dekompozíciónak az eredményeképpen juthatunk a torzítás-variancia dilemmához.

Torzítás-variancia dilemma

Bontsuk fel a (2.13) kifejezést a következő módon:

. $\begin{array}{l}MSE\left(w\right)=E\left\{\left(f\left(x,w\right)-g\left(x\right)\right){}^2\right\}\\ =E\left\{\left(g\left(x\right)-E\left\{f\left(x,w\right)\right\}+E\left\{f\left(x,w\right)\right\}-f\left(x,w\right)\right){}^2\right\}\\ =\left(g\left(x\right)-E\left\{f\left(x,w\right)\right\}\right){}^2+E\left\{\left(f\left(x,w\right)-E\left\{f\left(x,w\right)\right\}\right){}^2\right\}\\ =B{}^2\left(w\right)+V\left(w\right)\end{array}$ . (2.14)

A felbontás szerint az átlagos négyzetes eltérés két tagjából az első, B²(w) a torzítás négyzete, a második, V(w) pedig a megoldás varianciája. A torzítás (bias) azt mutatja meg, hogy a tanuló rendszer leképezésének várható értéke mennyiben tér el a regressziós függvénytől, míg a variancia a leképezésnek a saját várható értékétől való átlagos négyzetes eltérését adja meg. A torzítás arra ad választ, hogy az adott függvényosztály − amit a háló típusa és architektúrája rögzít − mennyire alkalmas a kérdéses approximációs feladat megoldására, a variancia pedig a véges számú tanítópont következménye: azt adja meg, hogy a véges számú tanítópont felhasználásával konstruált háló válasza, $f\left(x,w\right)$ mennyire érzékeny arra, hogy egy adott problémából származó aktuális tanítóhalmaz épp milyen mintapontokból áll.

Azonos négyzetes hiba előállhat nagyobb torzítás és kisebb variancia vagy kisebb torzítás és nagyobb variancia mellett; a két eset eltérő jellegű approximációt jelent. A szabad paraméterek számának növelése és így a háló által megvalósított függvényosztály komplexitásának növelése a torzítás csökkentését eredményezi. Minél több a szabad paraméter, annál komplexebb leképezés megvalósítására lehet alkalmas a neuronháló. Elegendően nagyszámú szabad paraméter mellett a háló válasza a tanítópontokban akár tetszőlegesen kis hibájú is lehet, miközben a tanítópontok között a válasz a valódi leképezéstől jelentős mértékben eltérhet. Ezt az esetet, amikor a torzítás kicsi, de a variancia nagy túlilleszkedésnek (overfitting) nevezik. A variancia csökkentése elsősorban a felhasznált tanítópontok számának a növelésével, pontosabban a szabad paraméterek számának és a tanítópontok számának megfelelő összehangolásával lehetséges.

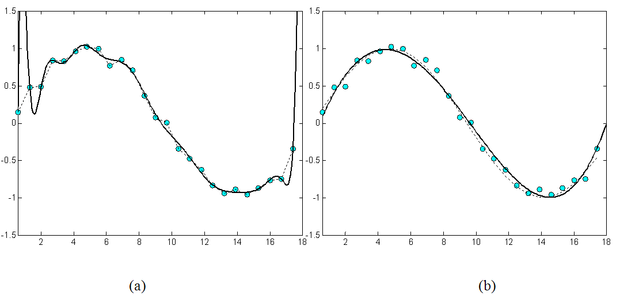
A túlilleszkedésre példa egy olyan polinomiális regresszió, amikor kevés mintapontra akarunk nagyfokszámú polinomot illeszteni. A 2.3 ábra egy szinuszos függvény polinomiális approximációját mutatja kissé zajos mintavételi pontok alapján. Az (a) ábrán egy túl nagy fokszámú (18-ad fokú) polinommal történő közelítés, a (b) ábrán egy 5-ödfokú polinom illesztésének az eredménye látható. Látható, hogy a fokszám csökkentésével − esetleg a mintapontokbeli tökéletes illeszkedés rovására − a pontsorozat általános trendjének követése inkább lehetséges.

A torzítás-variancia dilemma tehát azt a kérdést veti fel, hogy hogyan viszonyuljon egymáshoz a kétféle hibakomponens. A kérdés szorosan összefügg a háló típusának és méretének (komplexitásának) a megválasztásával, de kapcsolatban van a tanítópontok számával és magával az alkalmazott tanuló eljárással is. Az átlagos négyzetes hiba ilyen felbontása tehát azáltal, hogy segít a hiba értelmezésében, fontos szerepet tölt be a hálók megfelelő konstrukciójában.

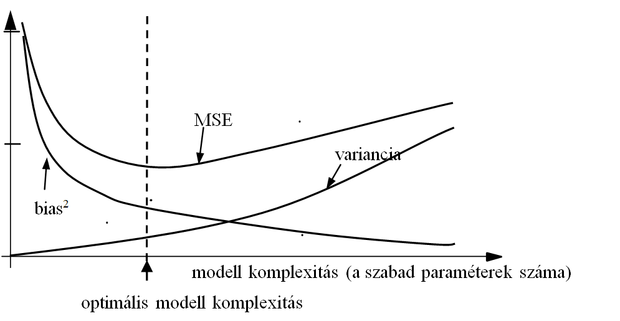
A torzítás-variancia dilemmát szemlélteti a 2.4 ábra. Látható, hogy az átlagos négyzetes értelemben legjobb megoldást nem a nagykomplexitású háló eredményezi, hanem az, ha a komplexitás összhangban van a tanítópontok számával és a feladat bonyolultságával.

Regularizáció

Mint láttuk, a véges számú mintapont alapján történő tanulási feladat rosszul definiált probléma. Egy feladatot rosszul definiáltnak (ill-posed) [Had02] nevezünk, ha

Mint ahogy a 2.1. ábra is illusztrálta, a véges számú pontból egy bemenet-kimenet leképezés megtanulása rosszul definiált probléma, mert a második feltételt nem teljesíti.

Az adatokból történő tanulás ugyanakkor ún. inverz probléma is. Tekintsünk egy $y=f\left(x\right)$ függvénykapcsolattal definiált leképezést. Ha a függvény ismert, adott x_i i=1, 2, … , l független változó értékekhez a megfelelő y_i függvényértékek egyértelműen meghatározhatók. Ezzel szemben, ha az összetartozó $\left\{x_i,d_i\right\}{}_{i=1}^l$ mintapontokat ismerjük, és ebből akarjuk visszaállítani az $y=f\left(x\right)$ függvényt, akkor egy inverz problémával állunk szemben. Az inverz problémák között számos rosszul definiált problémát találunk.

A neuronhálók tanításánál a rosszul definiáltság valójában azt jelenti, hogy a rendelkezésre álló információ − a tanítópontok együttese − az egyértelmű megoldáshoz nem elegendő. Egyértelmű megoldást csak további információ birtokában kaphatunk. Ilyen további információ lehet, hogy a megtanulandó leképezés − azon túl, hogy illeszkednie kell a tanítópontokra − legyen minél simább. Hasonló járulékos információként szolgálhat, ha egy kétosztályos osztályozási feladatnál arra törekszünk, hogy a két osztályt elválasztó felület ne csak elválassza a tanítópontokat, hanem az elválasztás minél nagyobb biztonsággal, tartalékkal valósuljon meg, az elválasztó felület az egyes osztályokba tartozó tanítópontoktól minél távolabb legyen,

A járulékos információkat be kell építenünk a probléma megfogalmazásába: a kockázat funkcionált járulékos taggal (tagokkal) kell kiegészítenünk. A járulékos tag mellékfeltételként vagy büntető tagként igyekszik a tanuló eljárást rákényszeríteni, hogy ne csak a kockázatot minimalizáló, hanem a mellékfeltételnek is eleget tevő megoldást kapjunk. Ha a kritériumfüggvényünket úgy módosítjuk, hogy a mintapontokra vonatkozó kockázatot kiegészítjük megfelelő mellékfeltétel(eke)t megfogalmazó taggal (tagokkal), regularizációról beszélünk [Tik77]. Regularizált esetben a kockázat helyett egy

$R_r\left(w\right)=R\left(w\right)+\lambda \Omega \left(w\right)$ (2.15)

kifejezés minimumát (szélső értékét) biztosító paramétervektort keresünk, ahol R(w) az eredeti kockázat, $\Omega \left(w\right)$ a regularizációs feltételt megfogalmazó járulékos komponens és λ az ún. regula-rizációs együttható. A járulékos tag valamilyen plusz feltétel, kényszer figyelembevételét szolgája, amely tükrözhet meglévő a priori információt, megfogalmazhat valamely, a realizációval kapcsolatos kényszert, vagy csak egyszerűen segíthet a szélsőérték probléma megoldásában. A regulari-zációs együttható szerepe, hogy az eredő kockázatban biztosítsa az eredeti kockázat és a regulari-zációs feltétel megfelelő arányát. A regularizáció, melynek elméleti megalapozása Andrej Tyihonovtól származik [Tik77], általában a rosszul definiált feladatok megoldásában nyújt segítséget. A regularizációs technika alkalmazására példákat a további fejezetekben, konkrét hálók kapcsán mutatunk.

Minősítő és teszt minták alkalmazása, kereszt kiértékelés

A kockázat alkalmazása a tanítás alatt álló vagy a megtanított háló minősítésére csak elvi lehetőség, hiszen a várható érték számításához vagy a $p\left(x,d\right)$ együttes sűrűségfüggvény vagy a $P\left(x,d\right)$ együttes eloszlásfüggvény ismeretére lenne szükség. A mintákból történő tanulásnál ezeket azonban nem ismerjük, így a tanuló rendszer minősítésére a kockázat közvetlenül nem használható.

A kockázat közvetett meghatározásával lehetőségünk nyílna a tanuló rendszer minősítésére. Ekkor a tanítópontok alapján előbb az ismeretlen sűrűségfüggvényt becsüljük, majd annak ismeretében már tudunk becslést adni a kockázatra. A közvetett megoldás nehézsége, hogy a sűrűségfüggvény megfelelő pontosságú becsléséhez nagyszámú mintára van szükségünk. Hasznosabbnak bizonyul, ha nem ezt az utat választjuk, hanem a rendelkezésre álló mintapontokat mind a háló tanítására, mind annak minősítésére is közvetlenül felhasználjuk. Ez a megközelítés abból az általános elvből indul ki, hogy ne kíséreljünk meg egy speciális problémát egy nála nehezebb általános probléma megoldásának felhasználásával, indirekt úton megoldani [Vap95].

Amennyiben a sűrűségfüggvényt nem ismerjük, a kockázat alapján történő minősítés helyett a minősítésre is csak a rendelkezésünkre álló mintapontokat használhatjuk. Mást nem tehetünk, minthogy az ismert válaszú pontok esetében meghatározzuk a tanuló rendszer válaszának hibáját. Ezen pontok hibájának átlagát empirikus vagy tapasztalati kockázatnak (empirical risk) nevezzük. Az l ismert tanító pontpár esetében a tapasztalati kockázat:

$R_{\text{emp}}\left(w\right)=\frac{1}{l}{\displaystyle \sum _{i=1}^{l}L\left(d_i,f\left(x_{i}w\right)\right)}$ , (2.16)

vagyis a tanítópontokban meghatározott veszteség átlaga.

Amennyiben a tapasztalati kockázatot a tanulásnál felhasznált mintapontokra számítjuk, a háló általánosító-képességéről általában semmit sem mondhatunk. A már említett túlilleszkedés miatt ugyanis előfordulhat, hogy a háló a tanítópontokat nagy pontossággal megtanulta, miközben a tanítópontoktól eltérő pontoknál a hiba nagyon nagy is lehet. A háló általánosítóképességének jellemzésére olyan mintapontokra kell meghatároznunk a tapasztalati hibát, melyeket a tanításnál nem használtunk fel.

Ennek érdekében egy külön kiértékelő (validation) mintakészletet kell használnunk, melynek mintái ugyancsak a megoldandó feladatból származnak, de amelyek függetlenek a tanító készlettől. A kiértékelő mintakészletet sokszor a tanítás folyamata alatt, a tanulás előrehaladtának értékelésére használjuk. Így, annak ellenére, hogy ezen minták nem tartoznak a tanításnál közvetlenül felhasznált mintapontok közé, közvetve részei a tanuló eljárásnak. A megtanított háló minősítésére ekkor egy ettől is független mintakészlet, a tesztkészlet szolgálhat. A tesztkészlet szintén az adott problémából származó összetartozó be-kimeneti mintapárok halmaza. A tesztkészlet mintapontjait azonban a tanításnál sem közvetlenül, sem közvetve nem használjuk fel. A tesztkészlet a megtanított háló végső értékelésére, a háló általánosítóképességének a becslésére használható.

A rendelkezésre álló mintapontokat egy problémánál ezért három részre, tanító-, értékelő- és tesztelő készletre kell bontanunk. Kellően nagyszámú adat mellet ez nem okoz nehézséget. Ha azonban kevés adat áll rendelkezésünkre (ez számos gyakorlati feladatnál előfordulhat vagy az adatok beszerzésének nagy költsége, vagy az adatoknak a probléma természetéből adódó kis száma miatt) a három diszjunkt készletre bontás azt eredményezheti, hogy az egyes részfeladatok elvégzéséhez túl kevés mintapontunk marad. Így, ha viszonylag sok pontot használunk fel a tanításra és kevés marad a megtanított hálózat minősítésére, nem lehetünk biztosak a megtanított hálózat képességeit illetően. Ezzel szemben, ha a minősítésre hagyunk több mintapontot és ezért kevés tanító pontunk lesz, csak azt konstatálhatjuk − bár ezt kellő biztonsággal tehetjük −, hogy a hálónk meglehetősen gyengén tanulta meg a feladatot. Ekkor, mint ahogy a (2.14) összefüggésből is látható az eredő hiba variancia komponense lehet nagy. Az egyes részhalmazok közötti megfelelő arányok meghatározása meglehetősen nehéz feladat. Erre vonatkozó néhány eredményt, melyet Shun-ichi Amari és munkatársai dolgoztak ki [Ama97], a 4. fejezetben fogunk röviden bemutatni.

Az ellentmondás egy lehetséges feloldására ún. kereszt kiértékelési (cross validation) eljárás alkalmazható (pl. [Sto78]). Ennek során a rendelkezésre álló mintapontokat véletlenszerűen felosztjuk k diszjunkt részhalmazra, majd k-1 részhalmaz pontjait tanításra, a maradék részhalmaz pontjait pedig kiértékelésre használjuk. Az eljárást megismételjük az összes részhalmazra úgy, hogy a tanítópontok közül mindig más-más részhalmazt hagyunk ki és használunk kiértékelésre. A hálózat eredő minősítését az egyes kiértékelések átlagaként nyerjük. Az eljárás előnye, hogy a rendelkezésre álló pontok jelentős részét felhasználjuk a hálózat tanítására, miközben az eredő értékelést az összes pont alapján végezzük, de úgy, hogy egy adott tanítást követően a háló értékelése mindig csak olyan pontokkal történik, melyeket az adott tanításnál nem használtunk fel. Hátrányként a hosszabb számítási időt említhetjük, hiszen a feladatot most k-szor kell megtanítanunk. Nagyon kevés rendelkezésre álló pont esetén a részhalmazok száma megegyezhet a pontok számával (k=l), ekkor minden tanítás l-1 ponttal történik, a minősítésre pedig a kihagyott pontot használjuk. Az eljárást itt is l-szer végezzük el, tehát végül itt is az összes pont alapján történik a megtanított háló minősítése. A kereszt kiértékelést ebben az esetben egy-kihagyásos (leave-one-out, loo) eljárásnak hívjuk.

Az itt említett eljárások a tapasztalati hibát alkalmazzák a megtanított háló minősítésére. Láttuk azonban, hogy ha a tapasztalati hibát a tanításnál ténylegesen felhasznált pontokra számítjuk, az általánosítóképességről nem kapunk megbízható információt. Amennyiben viszont független tesztkészletet használunk, a rendelkezésre álló ismert válaszú pontok korlátozott száma okozhat nehézségeket. További gondot jelent, hogy, még ha a tanító készlettől független tesztkészletet használunk is a minősítésre, a tapasztalati hibát mindenképpen véges számú pont alapján számítjuk. A tapasztalati kockázat tehát csupán becslése a valódi kockázatnak, és − különösen kevés teszt adat mellett − a becslés nagyon pontatlan is lehet. Alapvetően fontos ezért annak a kérdésnek a megválaszolása, hogy a tapasztalati hiba alapján állíthatunk-e valamit a (2.7) összefüggéssel definiált valódi kockázatról, és ha igen, akkor ez milyen feltételek mellett tehető meg. Erre a kérdésre az elsősorban Vladimir Vapnik nevéhez fűződő statisztikus tanuláselmélet (statistical learning theory) ad választ, melynek alapjait a 2.3. alfejezetben foglaljuk össze.