10.3. Nemlineáris PCA és altér hálók

10.3.1. Nemlineáris PCA és altér hálók

A független komponens analízis (ICA) feladat megoldására számos algoritmus született és ezen algoritmusok többsége szabadon felhasználható programcsomag, toolbox formájában hozzá is férhető. A következőkben a FastICA algoritmus működésének szemléltetésére mutatunk be néhány példát. Az első két példa összekevert képek szétválasztását mutatja be, a további példák pedig a koktélparti probléma (beszédjelek szétválasztása) egy lehetséges megoldását, illetve egyéb hangjelek szétválasztását illusztrálja. A példák, azon túl, hogy az algoritmus gyors működését illusztrálják, bemutatva, hogy néhány iterációs lépés elegendő a kevert jelek szétválasztására, egy, a megoldást biztosító szabadon hozzáférhető FastICA programcsomagra is felhívják a figyelmet.

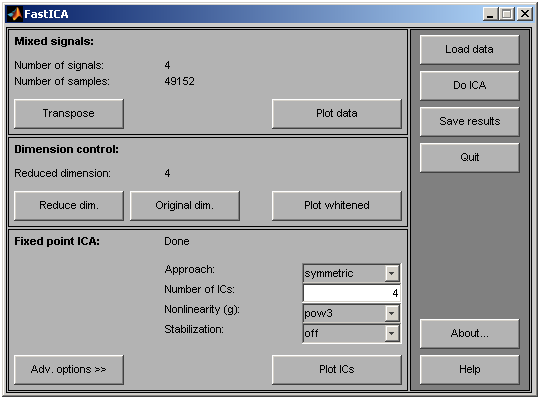
A FastICA for Matlab 7.x and 6.x (Copyright (c) Hugo Gävert, Jarmo Hurri, Jaakko Särelä, and Aapo Hyvärinen) programcsomag szabadon letölthető a http://research.ics.tkk.fi/ica/fastica/ honlapról. A program egy könnyen használható grafikus felülettel rendelkezik, ahol be lehet állítani az algoritmus paramétereit.

10.4.1-1. ábra - Grafikus felület
Grafikus felület

A témához kapcsolódó további információk a http://www.cs.helsinki.fi/u/ahyvarin/papers/fastica.shtml címen találhatók.

példa: fekete-fehér képek szétválasztása

A példa során három fekete-fehér kép és egy „zaj” összekevert képein mutatjuk be a FastICA algoritmus működését.

Az eredeti képek:

A következő képeken látható a keverés eredménye, amelyet egy 4x4-es véletlen számokból álló keverő mátrix eredményezett. A megfigyelt jeleket ( x MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFG0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWH4baaaa@36B3@ ) tehát az x=As MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFG0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWH4bGaeyypa0JaaCyqaiaahohaaaa@397F@ összefüggés szerint keverjük az s MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFG0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWHZbaaaa@36AE@ kiinduló jelekből (forrásokból), ahol A MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFG0dg9qqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWHbbaaaa@367C@ a keverő mátrix.

Az összekevert képek:

Az algoritmus néhány lépés alatt konvergált. A bemutatott ábrasorozat 6 iterációs lépés eredményeit mutatja. Az egyes lépések után fennálló közbenső eredmények és a 6. lépés utáni végeredménynek tekintett eredmény látható a következő ábrákon. A FastICA algoritmus a többi független komponens analízis algoritmushoz hasonlóan a komponenseket egy skalár szorzótényezőtől eltekintve határozza meg, tehát az eredmény nem egyértelmű és az eredeti képek a visszaállított képek skalárszorosaként kaphatók meg, vagyis a képeket utólag az előírt határok közé vissza kell skálázni. Előfordulhat az is – mint az a következő képeken meg is figyelhető –, hogy eredményként egyes képek negatívját kapjuk, ezért az egyes lépéseknél a közbenső eredményképek negatívjait is bemutatjuk.

1. lépés:

negatív

2. lépés:

negatív

3. lépés:

negatív

4. lépés:

negatív

5. lépés:

negatív

Végeredmény (6. lépés):

negatív

példa: színes textúrák:

A következő példában a kiinduló képeken sokkal inkább különböző textúrák láthatók, mint eltérő alakzatok. Ebben a példában a következő ábrán látható színes textúrák szerepelnek.

Az eredeti képek:

A keverő mátrix itt is egy 4x4-es véletlen számokból álló mátrix. A következő képeken látható az algoritmus egyes iterációs lépései után a képek alakulása.

Az összekevert képek:

1 lépés:

negatív

2 lépés:

negatív

3 lépés:

negatív

4 lépés:

negatív

5 lépés:

negatív

Végeredmény (6. lépés):

 

 

 

 

negatív

 

 

 

 
   

 

 

 

Az eredményképeken látható, hogy a visszaállítás nem minden tekintetben tökéletes. Eltérés lehet a kép színében (az eredeti 3. kép és a visszaállított 4. kép), de a 2. kép esetében az is látható, hogy a visszaállítás még nem sikerült maradéktalanul: a 2. visszaállított kép még jelentős arányban tartalmazza az 1. képet is.

példa: beszédjelek szétválasztása

A példa során 4 különböző beszédjel összekeverésével létrejött jelekre alkalmazzuk a FastICA algoritmust. Az algoritmus működésének eredményét megfigyelhetjük lépésről lépésre a jelalakok megtekintésével. Továbbá az összes kirajzolt jel .wav formátumban is rendelkezésre áll, így meghallgatható.

Az eredeti hangjelek (kiinduló jelforrások) időfüggvényei:

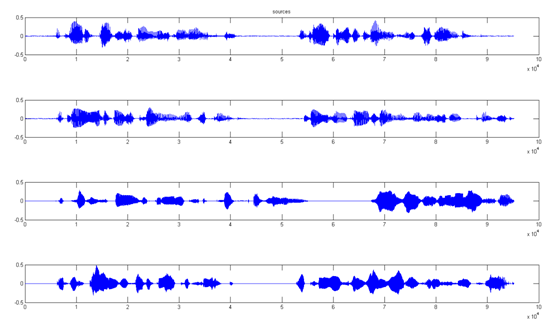
A jelek összekeverése egy 4x4-es véletlen számokat tartalmazó keverő mátrixszal történt, ennek eredménye látható a következő ábrán.

kevert jelek időfüggvénye:

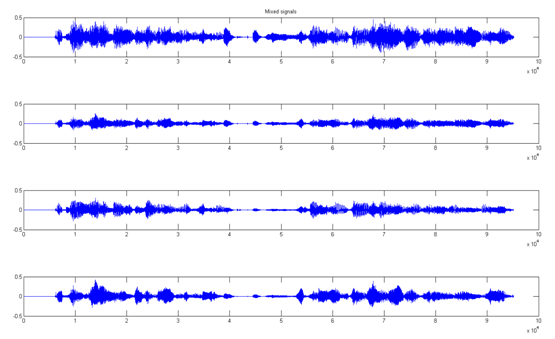
Az algoritmus 7 lépés alatt konvergált, az egyes lépések után kialakuló eredményt mutatják az alábbi ábrák.

1. lépés után:

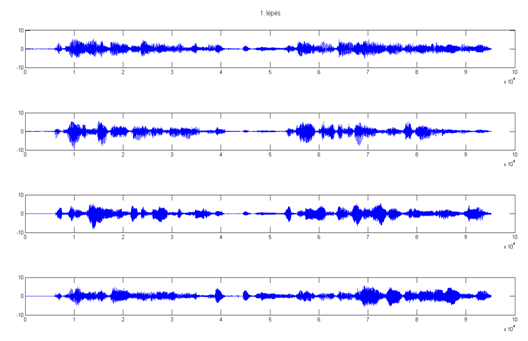
2. lépés után:

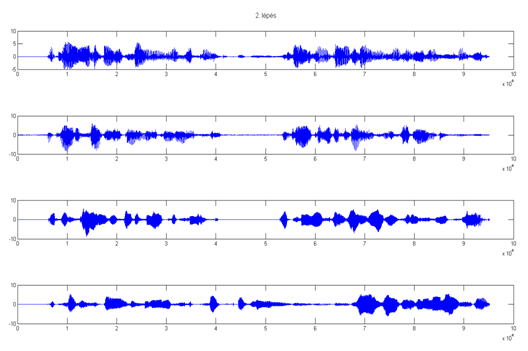
3. lépés után:

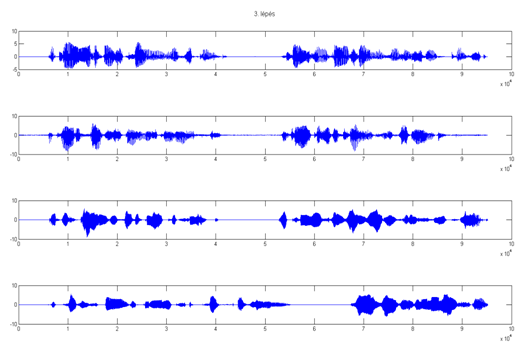
4. lépés után:

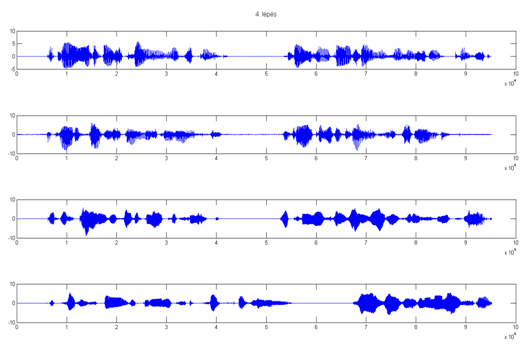
5. lépés után:

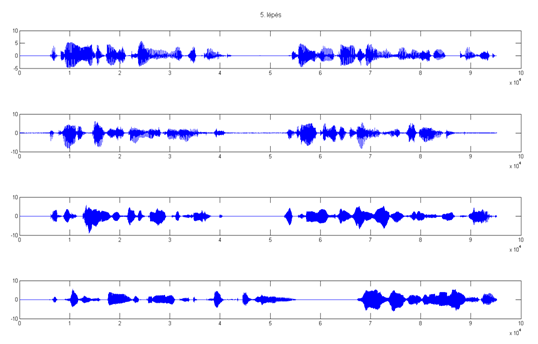
6. lépés után:

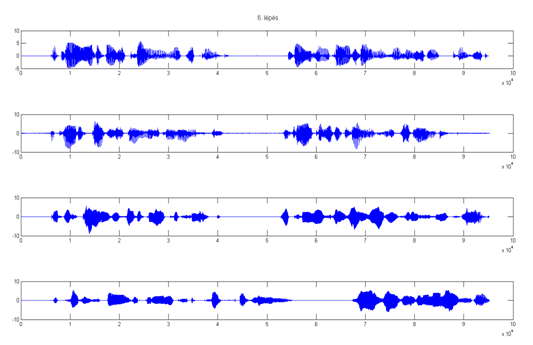
7. lépés után (végeredmény):

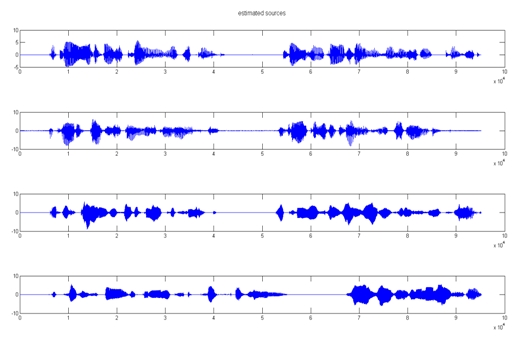
A végeredménynek az eredeti jelekkel való összevetéséből látható, hogy a jelek sorrendje megváltozott, továbbá, hogy az első eredeti jel negatív konstansszorosa jelent meg második szétválasztott jelkomponensként.

példa: vegyes hangjelek (beszéd és zene) szétválasztása

A következő példában három zenei jel, egy beszédjel és egy utcazaj szétválasztását végezzük el. A keverés itt is egy véletlen számokból álló keverő mátrixszal történt. A jelek alakulása itt is követhető lépésről lépésre.

Az eredeti jelek időfüggvényei:

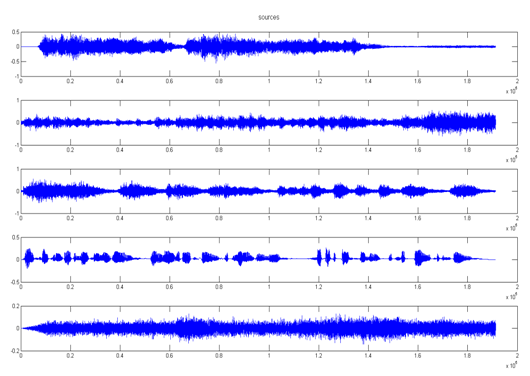
A kevert jelek:

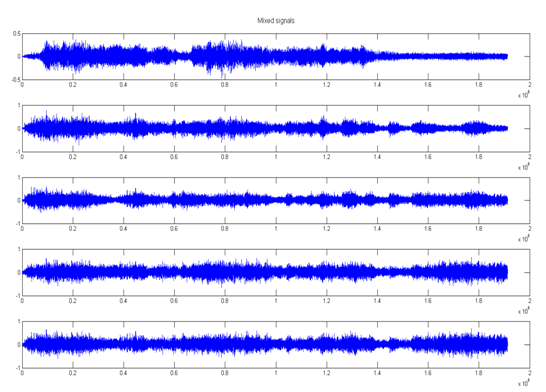
1. lépés után:

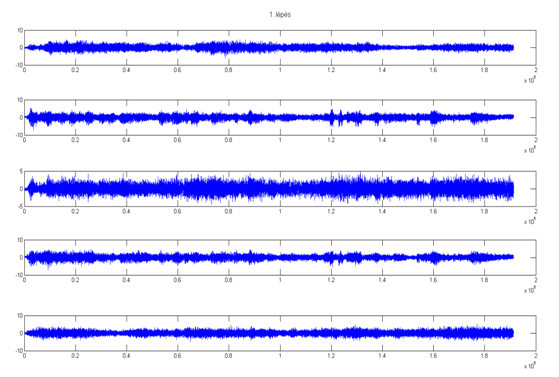
2. lépés után:

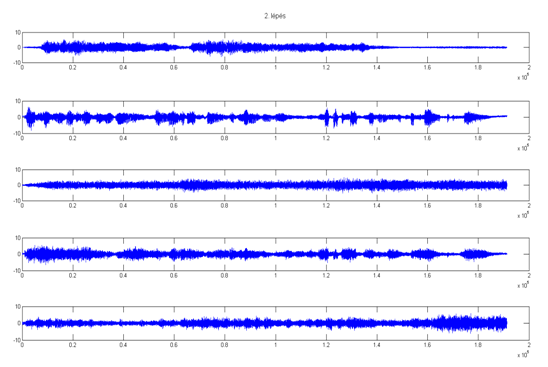
3. lépés után:

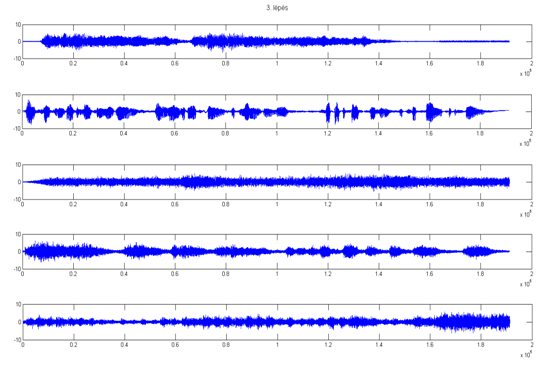
4. lépés után:

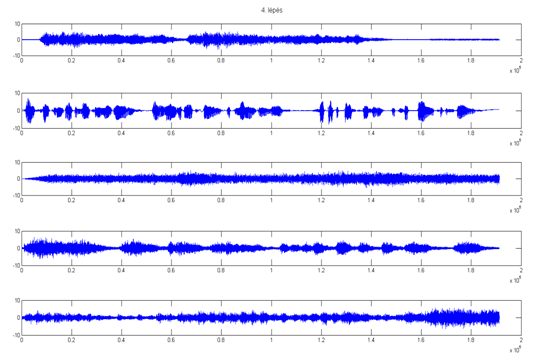
5. lépés után:

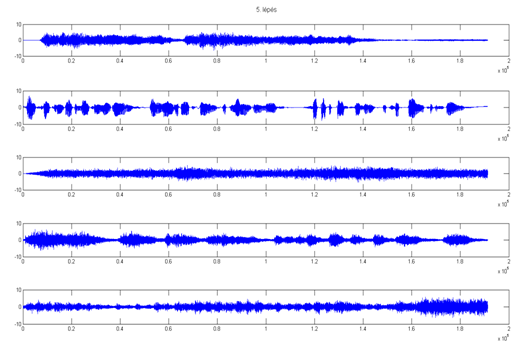
6. lépés után (végeredmény):

példa: szinusz jelek

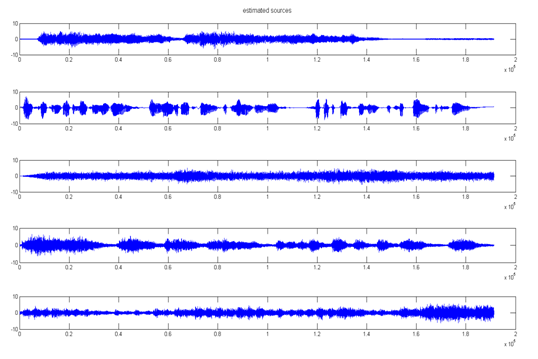
Ebben a példában egy olyan feladatot mutatunk be, ahol a független komponens analízis módszerek nem képesek a kevert jelet komponenseire szétválasztani. Ha az összekevert jelek komponenseire a függetlenség kritériumai nem teljesülnek az ICA módszerek a jel komponenseinek meghatározására alkalmatlanok. Bár ilyen esetekben a független komponens analízis algoritmusai nem alkalmasak a jel komponenseinek meghatározására, más jelszeparáló eljárás alkalmas lehet a szétválasztásra. Legyen a feladat különböző frekvenciájú szinusz jelek keverékének a szétválasztása. Mivel az összekevert jelek nem függetlenek, a feladat az ICA algoritmusok számára nem megoldható. Ezt illusztrálja a következő képsorozat:

Az eredeti jelek:

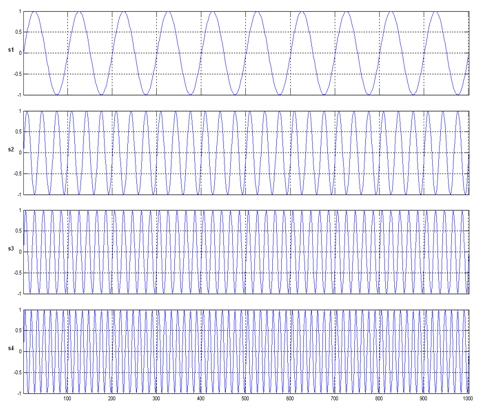
A kevert jelek:

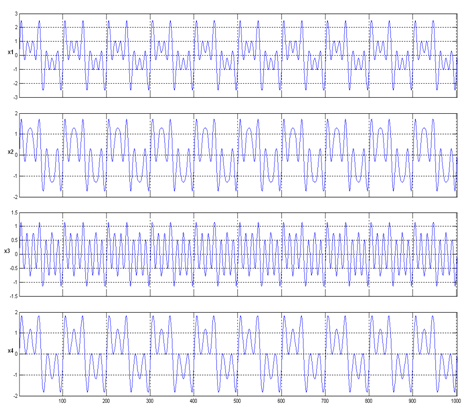
Az eredményként kapott jelek FastICA algoritmus alkalmazásával:

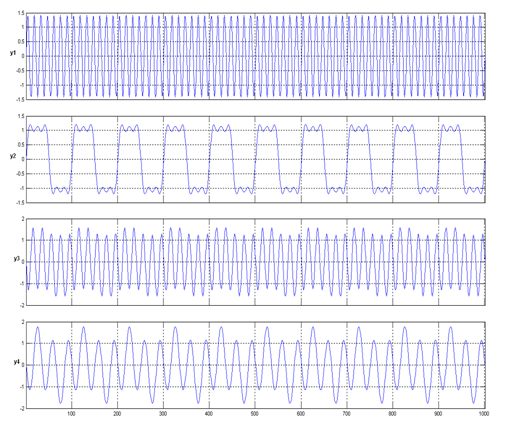
Látható, hogy nem sikerült szétválasztani a jeleket. Másodrendű statisztikán alapuló forrás szétválasztó algoritmusok számára viszont ez egy „egyszerű” feladat.

eredmény AMUSE algoritmussal:

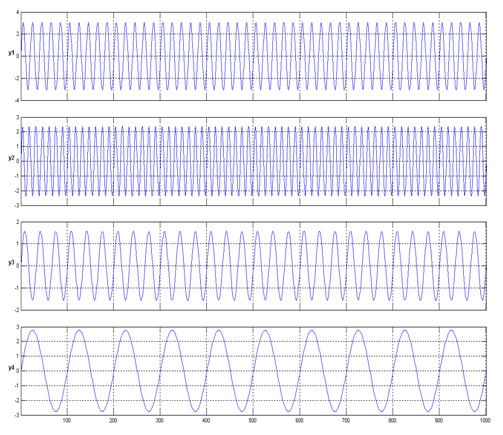
Az AMUSE algoritmus részletes bemutatása az irodalomban pl. [1], [2], [3] megtalálható. Itt csupán az algoritmus fő lépéseit foglaljuk össze.

AMUSE algoritmus:

  1. adatok fehérítése

  2. autó-kovariancia mátrix kiszámítása: R x (τ)=E   R x (τ)=E( ( s(t+τ)−E(s(t)) ) ( s(t)−E(s(t)) ) T ) MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaqabeaadaaakeaacaWGsbWaaSbaaSqaaiaadIhaaeqaaOGaaiikaiabes8a0jaacMcacqGH9aqpcaWGfbGaaGjbVlaaysW7caWGsbWaaSbaaSqaaiaadIhaaeqaaOGaaiikaiabes8a0jaacMcacqGH9aqpcaWGfbWaaeWaaeaadaqadaqaaiaadohacaGGOaGaamiDaiabgUcaRiabes8a0jaacMcacqGHsislcaWGfbGaaiikaiaadohacaGGOaGaamiDaiaacMcacaGGPaaacaGLOaGaayzkaaWaaeWaaeaacaWGZbGaaiikaiaadshacaGGPaGaeyOeI0IaamyraiaacIcacaWGZbGaaiikaiaadshacaGGPaGaaiykaaGaayjkaiaawMcaamaaCaaaleqabaGaamivaaaaaOGaayjkaiaawMcaaaaa@5E5E@ R transzformációs tulajdonsága: R A S (τ)=A⋅ R S (τ)⋅ A T MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaqabeaadaaakeaacaWGsbWaaSbaaSqaaiaadgeacaaMe8Uaam4uaaqabaGccaGGOaGaeqiXdqNaaiykaiabg2da9iaadgeacqGHflY1caWGsbWaaSbaaSqaaiaadofaaeqaaOGaaiikaiabes8a0jaacMcacqGHflY1caWGbbWaaWbaaSqabeaacaWGubaaaaaa@463F@

  3. szimmetrikus auto-kovariancia mátrix diagonizálása szimmetrikus auto-kovariancia mátrix: R _ x (τ)= 1 2 ( R x (τ)+ R x (τ) T ) MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaqabeaadaaakeaadaadaaqaaiaadkfaaaWaaSbaaSqaaiaadIhaaeqaaOGaaiikaiabes8a0jaacMcacqGH9aqpdaWcaaqaaiaaigdaaeaacaaIYaaaamaabmaabaGaamOuamaaBaaaleaacaWG4baabeaakiaacIcacqaHepaDcaGGPaGaey4kaSIaamOuamaaBaaaleaacaWG4baabeaakiaacIcacqaHepaDcaGGPaWaaWbaaSqabeaacaWGubaaaaGccaGLOaGaayzkaaaaaa@474A@ diagonizálás: R _ x (τ)=Q⋅Λ⋅ Q T =A⋅ R _ S (τ)⋅ A T MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaqabeaadaaakeaadaadaaqaaiaadkfaaaWaaSbaaSqaaiaadIhaaeqaaOGaaiikaiabes8a0jaacMcacqGH9aqpcaWGrbGaeyyXICTaeu4MdWKaeyyXICTaamyuamaaCaaaleqabaGaamivaaaakiabg2da9iaadgeacqGHflY1daadaaqaaiaadkfaaaWaaSbaaSqaaiaadofaaeqaaOGaaiikaiabes8a0jaacMcacqGHflY1caWGbbWaaWbaaSqabeaacaWGubaaaaaa@4DFC@ ahol Λ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaqabeaadaaakeaacqqHBoataaa@332F@ : sajátértékekből álló diagonális mátrix, Q: sajátvektorokból álló mátrix

  4. A becslése a sajátvektorokból álló mátrixszal

ha a források szimmetrikus auto-kovariancia mátrixának n (jelek száma) különböző sajátvektora van, akkor a keverő mátrix egyértelműen (kivéve oszlopok sorrendje, nagyságrend) meghatározható.

[1] L. Tong, V. Soon, Y. F. Huang, and R. Liu, Indeterminacy and identifiability of blind identification , IEEE Trans. CAS, vole. 38, pp. 499-509, March 1991.

[2] L. Tong, Y. Inouye, and R. Liu, Waveform-preserving blind estimation of multiple independent sources , IEEE Trans. on Signal Processing, 41 (7), pp. 2461-2470, July 1993.

[3] http://www.biologie.uni-regensburg.de/Biophysik/Theis/research/fmriWorkshop/slides_theis.pdf

Ez a példa ICALAB for Signal Processing programmal készült. A programban több független komponens analízis algoritmust implementáltak, így a különböző módszerek összehasonlítására is alkalmas.

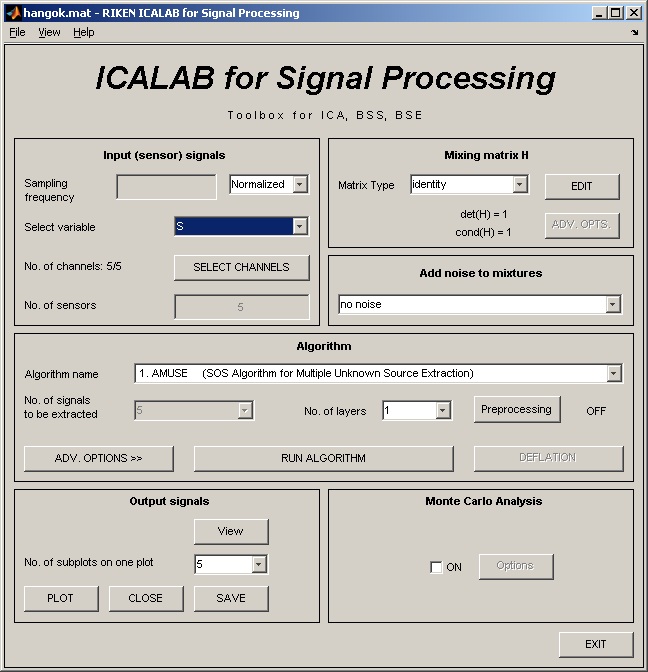
A program részletes leírása, és az implementált algoritmusok megtalálhatók a http://www.bsp.brain.riken.jp/ICALAB/ICALABSignalProc/ honlapon