Érdemes felrajzolni a konkrét kiterített hálót, a konkrét értékekkel, és a nullaértékű súlyokat kihagyni. Ezáltal egyszerűsödik a hibavisszaterjesztés. Számba kell venni azt, hogy a kérdéses súly hányszor és hol szerepel a kiterített hálóban, illetve megváltoztatása milyen uton hat az egyes időpontokban észlelhető kimenetekre.

Látható, hogy az adott időablakba kiterített hálónál a kérdéses súly három helyen is szerepel, ezeket az ábrán vastagítással jelöltük. Mivel most erre az egy súlyra koncentrálunk, és kényelmetlen sok alsó, felső indexet kezelni, ezért a súly három példányát p’, p’’, p’’’-vel jelöltük.

A tanítás során az időablakba eső négyzetes hibaösszeget (vagy átlagos négyzetes hibát) igyekszünk minimalizálni, ennek megfelelően mind a három időpontbeli pillanatnyi hibát bele kell vennünk a tanítási összefüggésbe. A három hiba elvileg függhetne a vizsgált súlynak mind a három példányától, de az ábrán látható módon ε(3) csak p’-től függ az ε(4) p’-től és p’’-től ε(4) stb., tehát:

$\Delta w_2^{(2)}=\Delta p=-\mu \left(\frac{\partial e{(3)}^2}{\partial p\text{'}}+\frac{\partial e{(4)}^2}{\partial p\text{'}}+\frac{\partial e{(4)}^2}{\partial p\text{'}\text{'}}+\frac{\partial e{(5)}^2}{\partial p\text{'}}+\frac{\partial e{(5)}^2}{\partial p\text{'}\text{'}}+\frac{\partial e{(5)}^2}{\partial p\text{'}\text{'}\text{'}}\right)$

Mivel $\frac{\partial \epsilon {(k)}^2}{\partial p}=2\epsilon (k)\frac{\partial \epsilon (k)}{\partial p}$ , ezért $\epsilon (4)=0$ miatt a konkrét helyzetben két tag kiesik.

$\Delta w_2^{(2)}=\Delta p=-\mu \left(\frac{\partial e{(3)}^2}{\partial p\text{'}}+\frac{\partial e{(5)}^2}{\partial p\text{'}}+\frac{\partial e{(5)}^2}{\partial p\text{'}\text{'}}+\frac{\partial e{(5)}^2}{\partial p\text{'}\text{'}\text{'}}\right)$

A kimeneti neuron lineáris, ezért:

$\frac{\partial \epsilon {(3)}^2}{\partial p\text{'}}=2\epsilon (3)\frac{\partial \epsilon (3)}{\partial p\text{'}}=2\epsilon (3)\frac{\partial y(3)}{\partial p\text{'}}=-2\epsilon (3)y_1^{(1)}(3)=-2(d(3)-y(3)).y_1^{(1)}(3)=-2.(-\mathrm{0,08})\mathrm{.0,7}$

A hibavisszaterjesztés $\epsilon (5)$ –ről p’-re a következő (vastagított vonalakkal jelölt) úton történik:

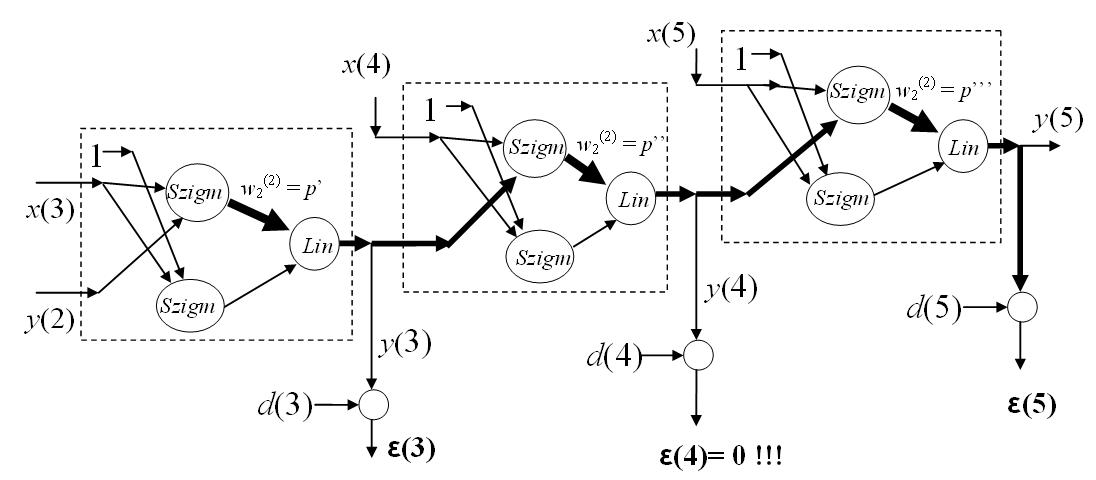
Ennek megfelelően:

$\begin{array}{l}\frac{\partial \epsilon {(5)}^2}{\partial p\text{'}}=2\cdot \epsilon (5)\cdot \frac{\partial \epsilon (5)}{\partial p\text{'}}=-2\cdot \epsilon (5)\cdot \frac{\partial y(5)}{\partial p\text{'}}=\\ =-2\cdot \epsilon (5)\cdot p\text{'}\text{'}\text{'}\cdot y_1^{(1)}(5)\cdot (1-y_1^{(1)}(5))\cdot w_{13}^{(1)}\cdot p\text{'}\text{'}\cdot y_1^{(1)}(4)\cdot (1-y_1^{(1)}(4))\cdot w_{13}^{(1)}\cdot y_1^{(1)}(3)=\\ =-2\cdot \mathrm{0,25}\cdot (-1)\cdot \mathrm{0,67}\cdot \mathrm{0,33}\cdot (-1)\cdot (-1)\cdot \mathrm{0,65}\cdot \mathrm{0,35}\cdot (-1)\cdot \mathrm{0,7}\end{array}$

Hasonlóképpen:

$\begin{array}{l}\frac{\partial \epsilon {(5)}^2}{\partial p\text{'}\text{'}}=-2\cdot \epsilon (5)\cdot p\text{'}\text{'}\text{'}\cdot y_1^{(1)}(5)\cdot (1-y_1^{(1)}(5))\cdot w_{13}^{(1)}\cdot y_1^{(1)}(4)=\\ =-2\cdot \mathrm{0,25}\cdot (-1)\cdot \mathrm{0,67}\cdot \mathrm{0,33}\cdot (-1)\cdot \mathrm{0,65}\end{array}$

és

$\frac{\partial \epsilon {(5)}^2}{\partial p\text{'}\text{'}\text{'}}=-2\cdot \epsilon (5)\cdot y_1^{(1)}(5)\cdot =-2\cdot \mathrm{0,25}\cdot \mathrm{0,67}$

Ezzel az összes kérdéses tagot felírtuk a konkrét számértékekkel.