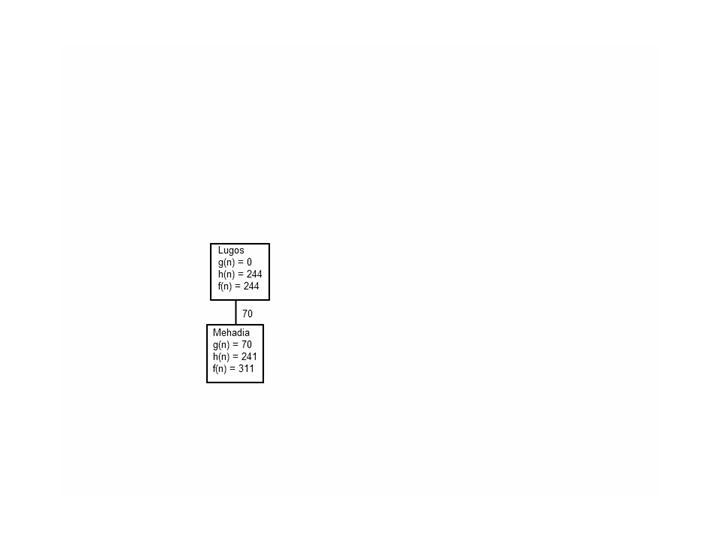
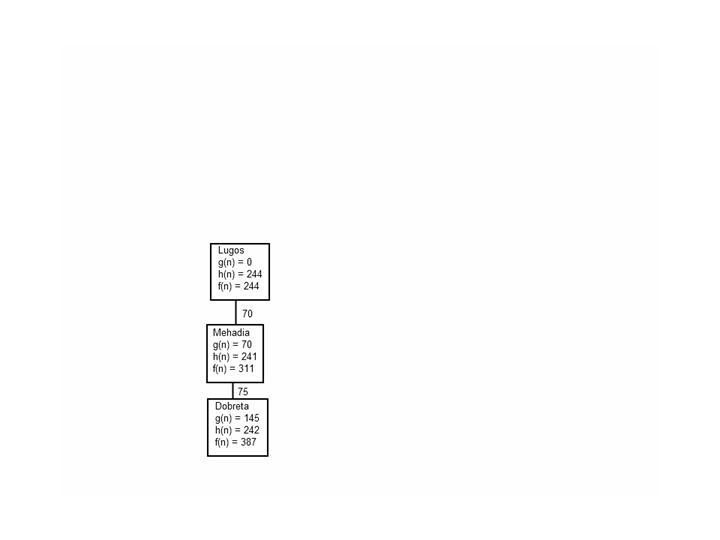
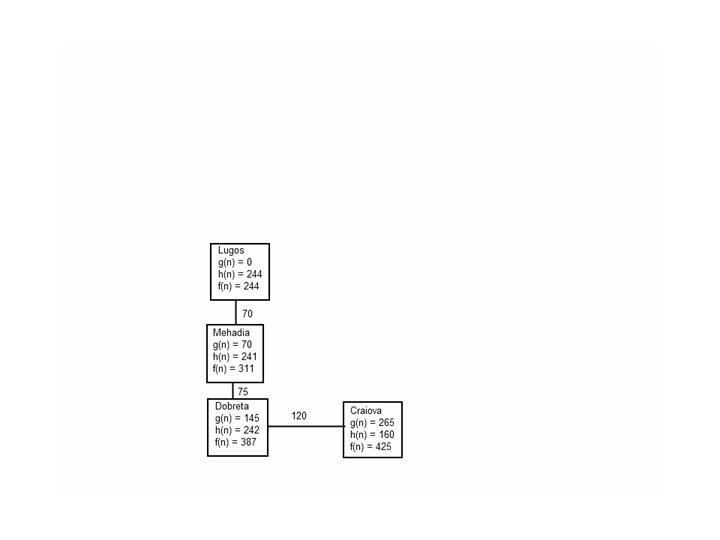
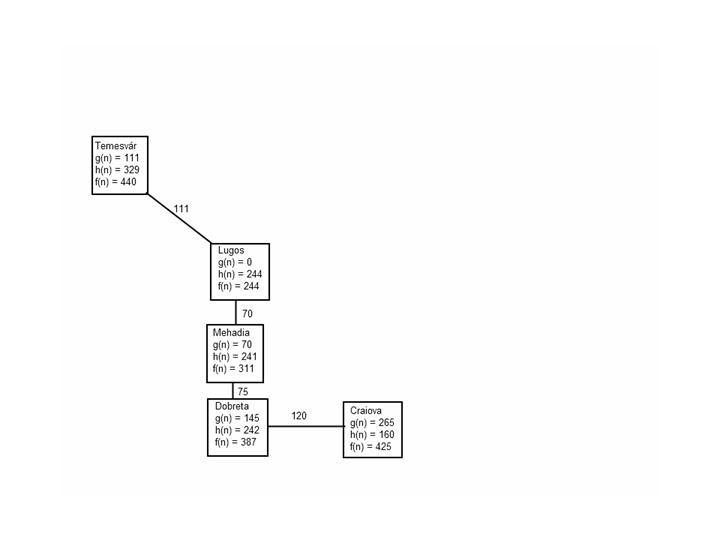
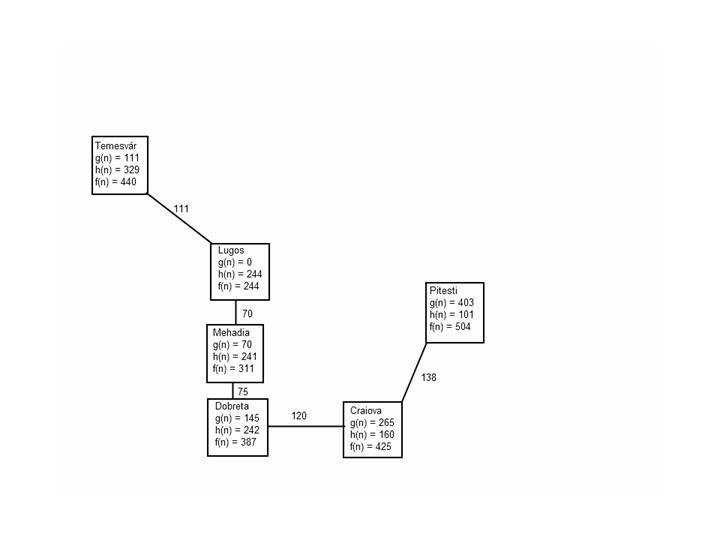
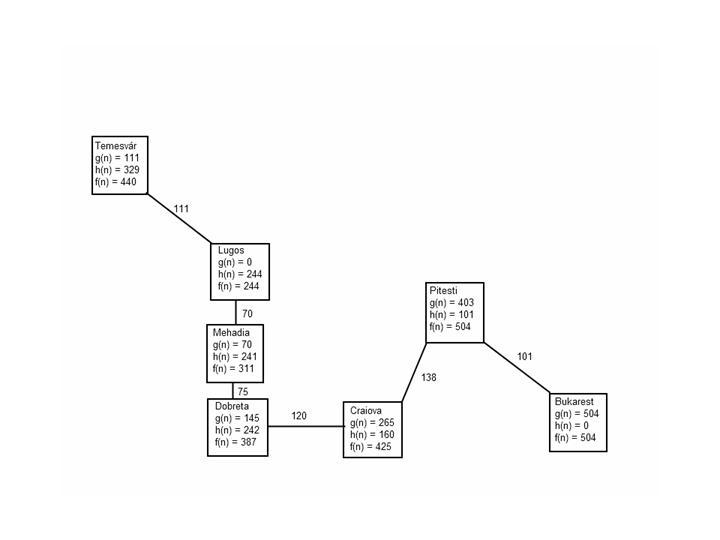
A* algoritmus esetén f(n) = g(n) + h(n), ahol g(n) a csomópontig megtett út költsége, h(n) pedig a heurisztikus függvény értéke az adott csomópontban. Előbbi a (könyvbeli) 3.2. ábráról olvasható le, utóbbi a 4.1. ábra táblázatában található meg.

i) A algoritmus optimális, ha 0 ≤ w ≤ 1. Intuitívan arról van szó, hogy az eddig megtett utat (amiről pontos adatunk van) nagyobb (pontosabban legalább akkora) súllyal kell figyelembe venni, mint a (csupán becslésre szolgáló) heurisztikus függvényt ahhoz, hogy a legolcsóbb utat találhassuk meg.

Formális bizonyítás: A megoldás akkor biztosan optimális, ha f(n) ≤ f(n’), azaz a kiértékelő függvény monoton. Ez azt jelenti, hogy h(n) ≤ h(n,n’) + h(n). Jelölje a két oldal különbségét E. Ekkor a fenti egyenlőtlenséget részletesen felírva:

(2-w)g(n) + w(h(n,n’) + h(n’) - E) = f(n) ≤ f(n’) = (2-w)g(n’) + wh(n’)

(2-w)g(n) + wh(n,n’) + wh(n’) - wE ≤ (2-w)g(n’) + wh(n’)

(2-w)g(n) + wh(n,n’) - wE ≤ (2-w)g(n’)

0 ≤ (2-w)g(n’) - (2-w)g(n) - wh(n,n’) + wE

Figyeljük meg, hogy g(n’) - g(n) = g(n,n’), azaz az n és n’ csúcs közötti út költsége! Ez azonban (mivel feltettük, hogy a heurisztika elfogadható) felülről becsülhető h(n,n’)-vel!

0 ≤ (2-w)g(n,n’) - wh(n,n’) + wE ≤ (2-w)g(n,n’) - wg(n,n’) + wE

0 ≤ (2-w)g(n,n’) - wg(n,n’) + wE

Most vonjuk össze a két g(n,n’) tagot:

0 ≤ (2-2w)g(n,n’) + wE

0 ≤ 2(1-w)g(n,n’) + wE

Tehát ennek az egyenlőtlenségnek kell teljesülnie ahhoz, hogy a megoldás garantáltan optimális legyen. Mivel E nemnegatív, ezért wE pontosan akkor lesz nemnegatív, ha 0 ≤ w. 2(1-w)g(n,n’) pedig pontosan akkor lesz nemnegatív, ha w ≤ 1, továbbá az útköltségekről feltesszük, hogy nem negatívak.

ii) w = 0: f(n) = (2-0)g(n) + 0h(n) = 2g(n). A heurisztikus függvény eliminálódik az egyenletből, tehát ez egy nem informált algoritmus. Lényegében (konstanssal való szorzástól eltekintve) megegyezik az egyenletes költségű kereséssel.

iii) w = 1: f(n) = (2-1)g(n) + 1h(n) = g(n) + h(n), azaz megegyezik az A* algoritmussal.

iv) w = 2: f(n) = (2-2)g(n) + 2h(n) = 2h(n). Az útköltség eliminálódik az egyenletből. Ez így egy általános legjobbat-először keresés.

a) A szélességi keresés az egyenletes költségű keresés egy speciális esete.

Legyen az élköltség minden él esetén egységnyi. Ekkor egy csúcshoz vezető út költsége megegyezik az útban szereplő élek számával, így a szélességi keresés megegyezik az egyenletes költségű kereséssel.

b) A szélességi keresés, a mélységi keresés és az egyenletes költségű keresés a legjobbat-először keresés speciális esetei.

Egy legjobbat-először keresés esetén f(n) = h(n) valamely heurisztikus függvényre.

- Legyen h(n) = -d(n), ahol d(n) startcsúcsból az adott csúcshoz vezető utak hosszának (a bennük lévő élek számának) minimuma. Az így kapott heurisztika épp a mélységi keresést adja.

- Legyen h(n) = d(n). (d(n)-t lásd fent.) Az így kapott heurisztika épp a szélességi keresést adja.

- Legyen h(n) = g(n). Az így kapott heurisztika épp az egyenletes költségű keresést adja.

c) Az egyenletes költségű keresés az A* keresés egy speciális esete.

Legyen h(n) = 0 minden csúcsra. Ekkor A* algoritmusnál f(n) = g(n) + 0 = g(n), ami éppen megegyezik az egyenletes költségű keresés képletével.

Itt a probléma az, hogy a GRÁF-KERESÉS algoritmus az ismétlő csúcsokat nem fogja újra kifejteni akkor sem, ha az új út olcsóbb, mint a korábbi.

Emlékeztetőül: elfogadható egy h(n) heurisztika, ha soha nem becsüli túl a cél elérésének költségét; konzisztens pedig akkor, ha bármely n csúcsból a cselekvéssel elérhető n' utódcsúcs esetén h(n) =< h(n') + c(n,a,n'), azaz a heurisztika nem becsüli túl a következő csúcs elérésének költségét.

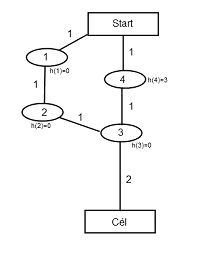
Olyan heurisztikát kell most tehát szerkesztenünk, ami a célhoz szükséges költséget nem becsüli túl, de a következő csúcs elérésének költségét túlbecsülheti. Tekintsük az ábrán látható állapotteret! A csúcsok sorszámai egyben jelzik a kifejtésük sorrendjét is.

A probléma abból adódik, hogy Iasiról Neamt felé indulva sokkal közelebb kerülünk Fogarashoz, mint Vaslui felé indulva, de Neamtból nem tudunk tovább menni. Az ellenkező irányban nincs ilyen probléma, de ez teljesen esetleges, ott is egészen könnyen előfordulhatna hasonló.

Példa:

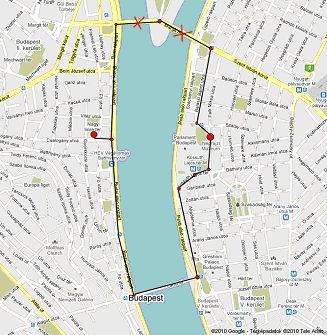
Tegyük fel, hogy a kezdőállapot a Nagy Imre tér, a célállapot pedig a Néprajzi Múzeum. Ekkor a légvonalban mért távolságheurisztika a Margit hídon felé indul el, ami azonban felújítás miatt nem használható (amit jelezhetünk például az átkelés útköltségét egy extremális elemnek választva), így vissza kell fordulnia, és a Lánchídon átkelni. A helyzet ugyanez fordítva is: a keresés előbb ellátogat a Margit híd pesti hídfőjéhez, majd visszafordul, mert átkelni már nem tud. A problémát a következő ábra szemlélteti. (Vegyük észre, hogy nem szükséges valódi zsákutcának lennie: a keresés tovább mehetett volna az Árpád-híd felé, de ez lényegesen költségesebb lett volna, mint a Lánchíd. Elég tehát egy kezdetben jónak tűnő, de végül mégis költségesnek bizonyuló útvonalat találni. Ebben rejlik az algoritmus mohósága: ha lát egy kecsegtető utat, rögtön lecsap rá.)

i) Vegyünk egy egészen ügyetlen heurisztikát, amely általában a Manhattan távolsággal dolgozik, de valamiért nem kedveli azokat az állapotokat, ahol a hatos mező a középen van. Ilyen esetekben hússzal nagyobb a függvény értéke. Tekintsük most a következő ábrát! A kezdőállapotból az optimális megoldás 10 lépéses (az alsó 2x3-as részt kell két lépésben körbeforgatni az óramutató járásának megfelelő irányban), de a heurisztika ezt a cselekvéssorozatot el fogja kerülni, mivel rögtön középre kéne tennie a hatos mezőt! Ehelyett egy szuboptimális, 20 lépéses megoldást nyújt (a megoldás maga hasonló a fentihez, csak most az óramutató járásával ellentétes irányban forgatjuk körbe az alsó részt).

Általában, ha egy feladatnál lehetséges cselekvések egy sorozatával ugyanabba az állapotba visszajutni, és a cselekvések megfordíthatóak, egy adott szituációban általában a cselekvéssorozat végrehajtásának egyik iránya célravezetőbb, mint a másik. Ilyenkor persze ezt érdemes választani, de ha valamiért a heurisztika nem tudja megmondani, hogy melyik irányban kell több lépést elvégezni a cselekvéssorozatból, az vezethet szuboptimális megoldáshoz.

ii) A feltétel szerint ha az algoritmus futása során valamely lépésben c-nél nagyobb különbség lenne az optimális út hátralevő részének költsége és h becslése között, akkor ezt az utat az algoritmus levágná. Következésképpen a végrehajtás során sehol nem lehet az út aktuális költsége több, mint c-vel magasabb, mint egy optimális megoldásé!

Konzisztens egy heurisztikus függvény, ha bármely n csúcs esetén a belőle a cselekvéssel elérhető bármely n' csúcsra h(n) ≤ c(n,a,n') + h(n'), azaz ha az algoritmus sosem becsüli túl a következő lépés költségét. Teljes indukcióval könnyen látható, hogy ekkor a teljes hátralevő utat sem fogja túlbecsülni, tehát elfogadható is. Ha n' egy célcsúcs, akkor h(n') = 0, h(n) ≤ c(n,a,n'), a célcsúcsot megelőző csúcsra tehát teljesül az elfogadhatóság követelménye. Tegyük fel, hogy bármely a céltól k csomópontra lévő m' csúcsra is teljesül. Ekkor bármely olyan m csúcs, amelyhez létezik olyan b cselekvés, amely m-ből m'-be visz, a konzisztencia definíciója miatt h(m) ≤ c(m,a,m') + h(m'). De mivel h(m') nem nagyobb, mint az m' csúcsból egy célcsúcsba jutás költsége, így a konzisztencia miatt h(m) sem nagyobb, mint az m'-be jutás költsége plusz az m'-ből egy célcsúcsba jutásé. Így tehát bármely m-re is teljesül az elfogadhatóság követelménye. Ezzel beláttuk, hogy bármely csúcs, amelyből létezik út egy tetszőleges célcsúcsba, kielégíti az elfogadhatóság feltételét, ha kielégíti a konzisztencia feltételét egy adott h esetén. Olyan csúcsokkal már nem is kell foglalkozni, amelyekből nem lehet eljutni egy célcsúcsba, hisz ezeknél a célcsúcsba jutás költsége tekinthető végtelen nagynak, ezért h tetszőlegesen nagy értéket vehet fel.

Egy elfogadható, de nem konzisztens heurisztika látható a 4.4 feladat ábráján.

a) Mutassa meg, hogy ez a heurisztikus függvény hogyan származtatható a TSP relaxált változatából!

Fogalmazzuk át úgy a feladatot, hogy egy kezdőpontból szeretnénk minden várost elérni úgy, hogy a kezdőpontba bármikor ingyen visszatérhetünk, és a megtett utak összköltségét szeretnénk minimalizálni. Ennek a feladatnak a megoldása a lehetséges utak gráfjának minimális feszítő fája.

b) Mutassa meg, hogy az MFF-heurisztika dominálja a légvonalban mért távolságheurisztikát!

Következik a háromszög-egyenlőtlenségből.

d) Keressen hatékony módszert az irodalomban az MFF megszerkesztésére, és használja azt egy elfogadható keresési algoritmussal a TSP-probléma egyedeinek a megoldására!

A két leggyakrabban használt algoritmus minimális feszítőfák meghatározására Kruskal illetve Prim algoritmusa. Előbbi minden lépésben megvizsgálja az aktuális legolcsóbb élt, és ha ezt az eddigi feszítőfához hozzávéve továbbra is fát kapunk, akkor felveszi a feszítőfába, ha pedig nem, akkor eldobja (többet nem vizsgálja meg). Utóbbi egy tetszőlegesen választott csúcsból indul, és minden lépésben hozzáveszi a legközelebbi, a fával szomszédos csúcsot, amit még nem vett hozzá eddig a fához, a legolcsóbb úttal, amin elérhető.

Forrás:

Minimális feszítő fa: http://en.wikipedia.org/wiki/Minimum_spanning_tree

Kruskal-algoritmus: http://en.wikipedia.org/wiki/Kruskal%27s_algorithm

Prim algoritmusa: http://en.wikipedia.org/wiki/Prim%27s_algorithm

(A Gascnig-heurisztika tehát azt mondja meg, hányszor kéne egy mezőt az üres mezővel kicserélni, hogy a célállapotot kapjuk.)

Amennyiben nincs 'körbetartozás' a mezők között (azaz A₁ mezőt A₂ helyére, A₂-t A₃-helyére,... A_n-t A₁ helyére kéne tenni), úgy a két heurisztika értéke megegyezik, hisz pontosan azokat a mezőket kell áthelyezni, amelyek rossz helyen vannak. Amennyiben van ilyen kör a mezők mozgatásában, úgy a Gaschnig-heurisztika értéke annyival nagyobb lesz, ahány kör előfordul: minden kör esetén először egy mezőt ideiglenesen ki kell venni a körből, hogy a többi a helyére kerülhessen! Mivel ezt a megoldás során valóban meg kell tenni, így a Gaschnig-heurisztika pontosabb közelítést ad.

Ha két egymás melletti mező az eredeti helyéhez képest fel van cserélve, akkor mind h₁, mind h₂ értéke kettő, míg a Gaschnig-heurisztika értéke három. A valójában szükséges lépések száma nyílván nagyobb lesz kettőnél, hisz nem lehetséges két mezőt két lépésben felcserélni, tehát a Gaschnig-heurisztika pontosabb a másik kettőnél.

A feladat relaxált verzióját kell megoldani. Ha az üres mező nincs a helyén, akkor cseréljük ki azzal a mezővel, amelynek a helyén van. Ha az üres mező a helyén van, de még nem vagyunk célállapotban, cseréljük ki az üres mezőt egy véletlenszerű, nem a helyén levő mezővel. Ismételjük ezt addig, amíg célállapotba nem jutunk.

Forrás: http://filebox.vt.edu/users/anithian/CS5804/HW1.pdf

A feladat lényegében könyvtárazás. Az igényesebb olvasó a javasolt írókon túlmenően megkeresheti Richard E. Korf írásait is.

a) Lokális nyaláb keresés k = 1 mellet.

A lokális nyaláb keresés egyszerre nem 1, hanem k különböző állapottal dolgozik. Amennyiben k = 1, úgy ez megegyezik a hegymászó módszerrel.

b) Lokális nyaláb keresés egy kezdeti állapottal és korlátlan számú visszatartott állapottal.

Itt a visszatartott állapot az, amelyet megtartunk a memóriában. Most tehát csak egy pontból indulunk el, és tetszőleges pontot tartunk észben, így ez a változat megegyezik egy véletlen csúcsból indított szélességi kereséssel.

c) Szimulált lehűtés, ha T = 0 minden időpillanatra (és kihagyva a leállási tesztet).

Szimulált lehűtés esetén T = 0 azt jelenti, hogy annak esélye, hogy egy olyan cselekvést válasszunk ki kifejtésre, amely a kiértékelő függvényt rontja, 0, azaz csak olyan lépéseket tesz meg, amelyek javítják a kiértékelő függvényt. Ez az eset tehát megegyezik a hegymászó módszerrel.

d) Genetikus algoritmus N = 1 nagyságú populációval.

Mivel csak egy elemű a populáció, nincs mód kiválasztásra és keresztezésre, csak a mutáció fázis változtatja meg a populáció egyetlen elemét, új 'generációt' létrehozva. Így tehát a sztochasztikus hegymászó kereséshez hasonlóan működik.

A legjobbat-először keresés elve igen egyszerű: az aktuális csúcs esetén megvizsgálunk minden legális cselekvéssel elérhető csúcsot, és kiválasztjuk ezek közül azt, amely várhatóan a legközelebb visz a célhoz. Az, hogy létezik összehasonlítási módszer, gyakorlatilag azt jelenti, hogy az egy csúcsból elérhető csúcsok halmaza rendezett, tehát létezik egy rajtuk értelmezett rendezési reláció, amely reflexív (A≤A), antiszimmetrikus (ha A≤B és B≤A, akkor A=B) és tranzitív (ha A≤B és B≤C, akkor A≤C). Az, hogy az összehasonlítás „jó”, azt jelenti, hogy a rendezés teljes, azaz bármely két csúcs esetén vagy A≤B vagy B≤A igaz (esetleg mindkettő). Viszont ha egy halmaz teljesen rendezett, akkor szükségképpen van maximuma, vagyis olyan X halmazbeli elem, amelyre igaz, hogy bármely halmazbeli A-ra A≤X. Ez az X lesz az, amelyet a best-first algoritmusnak ki kell választania.

Itt már gondban vagyunk. Az A* algoritmus egyszerre veszi figyelembe az eddig megtett utat, és a hátralevő út várható költségét. Egy olyan algoritmusnál, amelyik csak az egyiket veszi figyelembe, alkalmazható a fenti gondolatmenet, azonban az A* algoritmus esetén ezek összegére (illetve az összegek összehasonlítására) is szükség van. Tehát ahhoz, hogy az előzőhöz hasonló módszert szerkeszthessünk az A* analógiájára is, szükségünk van egy jó összehasonlítási módszerre, amely ('eddig-megtett-út','hátralevő-várható-út') párokat hasonlít össze. Ilyen összehasonlítási módszer létezése nem kizárt, de nem túl valószínű.

A 4.5 részből megtudtuk, hogy a TRTA* algoritmus időkomplexitása legfeljebb négyzetes, azaz az algoritmusnak O(n²) időre van szüksége a teljes környezet feltárásához, ha az n állapotból áll. A tárkomplexitása pedig O(n), ha minden állapotot feltár, és megjegyez. Általánosságban az algoritmus időkomplexitása a tárkomplexitás négyzetével arányos, azaz ha m csúcsot kell feltárnia a célállapot megtalálásához, akkor ehhez O(m²) időre lesz szüksége.

a) Magyarázza meg, hogy ezt az online keresési problémát hogyan lehet offline keresésnek tekinteni egy olyan hiedelmi állapottérben, ahol a kezdeti hiedelmi állapot a környezet minden lehetséges konfigurációját tartalmazza. Milyen nagy a kezdeti hiedelmi állapot? Milyen nagy a hiedelmi állapottér?

Legyen lehetséges állapot minden olyan állapot, ahol az ágens a kilenc mező valamelyikén helyezkedik el, és bármely helyen, ahol lehet fal, vagy van, vagy nincs. Így összesen 9*2¹² állapotot kapunk. A kezdeti hiedelmi állapot tartalmazza azokat az állapotokat, amelyekben az ágens a bal alsó sarokban helyezkedik el, és egyik lehetséges falról sem tudja, hogy ott van-e, vagy nincs. Amikor egy adott hiedelmi állapotot megvizsgál, megnézi, mely lépések legálisak az adott szituációban. Ez alapján átkerül egy másik hiedelmi állapotba, ahol az adott falról már tudja, hogy ott van-e, avagy nincs. Amerre nincs fal, arra tehet egy lépést, amellyel olyan hiedelmi állapotba kerül, amelyben egy másik helyzetben van, és még mindig emlékszik, hol volt fal, hol nem. Fontos szem előtt tartani azonban, hogy az ágens nem képes teleportálni, azaz mindig csak egy hiedelmi állapot szabad vizsgálni!

A kezdeti hiedelmi állapot tehát tartalmazza az összes olyan esetet, ahol az ágens a bal alsó sarokban van, és bármely helyen, ahol lehet fal vagy van fal, vagy nincs. Összesen tizenkét helyen lehet fal, tehát 2¹² = 4096 állapotot tartalmaz a kezdeti hiedelmi állapot.

Az ágens kilenc különböző helyen lehet, és tetszőleges mennyiségű helyről tudhatja (tapasztalatból), hogy van-e ott fal vagy nincs, azaz bármely potenciális fal esetén három lehetőség van: tudja, hogy van ott fal, tudja, hogy nincs ott fal, vagy nem tud semmit. A hiedelmi állapotok száma így 9*3¹² = 3¹⁴. Ennek persze 1/9-ed része célállapot és léteznek olyan hiedelmi állapotok, amelyek nem érhetők el a kezdőállapotból. (Például nincs olyan elérhető állapot, amelyben az ágens tudja, hogy a jobb felső 2x2-es négyzet el van zárva és azon belül a jobb felső 1x1-es négyzet is, hisz mivel a jobb felső 2x2-es négyzetbe nem tud bejutni, annak belsejéről semmilyen információt nem szerezhet.) A hiedelmi állapotok száma tehát ijesztően magas. A feladat ilyen irányú megoldása ennek ellenére nem kilátástalan, ugyanis a kapott gráf szerkezete rettentően összetett, megfelelő keresési módszerrel igen gyorsan található célállapot.

b) Hányféle különböző megfigyelés lehetséges a kezdeti állapotban?

Összesen négy lehetséges állapotot tud megkülönböztetni az ágens kezdetben:

c) Írja le a probléma esetén az eshetőségi terv néhány első ágát. Milyen nagy (nagyjából) az egész terv?

Ahogy fent láttuk, a hiedelmi állapotok száma igen nagy, és nagyon sok ezek közül elérhető a kezdőállapotból, így a teljes eshetőségi terv nagyon nagy lesz. Mivel azonban mindig csak egy úttal foglalkozunk, a tárigény nem lesz túl magas (elegendő egy konstans méretű vektort és egy egész értékű változót tárolni), és ha van megoldás, akkor legrosszabb esetben O(n) lépésben megtalálja az algoritmus (12 mozgás, ennél kevesebb körülnézés).

Jegyezzük meg, hogy ez az eshetőségi terv az adott leírást kielégítő minden lehetséges környezet számára megoldás. A keresés és a végrehajtás átlapolódása tehát egy ismeretlen környezetben nem szigorúan szükséges.

a) Tervezze meg a TSP megoldására a hegymászó keresést. Az eredményeket az MFF-heurisztikával (4.8. feladat) dolgozó A* algoritmus optimális megoldásaival hasonlítsa össze.

A feladat elsőre kicsit félrevezető. Az állapotok itt ugyanis a lehetséges körutak, amelyekből a minimális költségűt szeretnénk megtalálni, ellentétben a korábbi megközelítéssel, ahol a körút optimális felépítésével próbálkoztunk. Most tehát kiválasztunk egy tetszőleges körutat: ez lesz a kezdőállapot. Az aktuális körút szomszédjait úgy kapjuk meg, hogy felcseréljük két város sorrendjét. (Azaz ha (A₁,A₂,...,A_i,...,A_j,...,A_n) az aktuális állapot, és (A₁,A₂,...,A_j,...,A_i,...A_n) is egy legális körút, akkor ez egy eleme lesz a szomszédok halmazának.)

b) Tervezzen meg a TSP megoldására egy genetikus algoritmust. Az eredményeket más megközelítésekkel hasonlítsa össze. Esetleg szüksége lehet a (Larranaga és társai, 1999) cikk egyes reprezentációs javaslataira.

- A leggyakrabban használt reprezentációs módszer, hogy egy vektorként tároljuk a sorrendet úgy, hogy a vektor i-edik eleme a sorban i-edikként meglátogatott város sorszáma legyen (út-reprezentáció, path-representation). Az ötlet szépséghibája, hogy a mutáció során könnyen előfordulhat, hogy egy város többször is sorra kerülne. Ezen probléma orvoslására javító műveleteket kell bevezetni, amelyek a hibás egyedekből (invalid utakból) valamilyen módon szabályos egyedeket generálnak.

- Fitness függvénynek érdemes az összköltséggel arányos függvényt választani.

Larranaga és társai cikke (angol nyelven) megtalálható itt: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.118.2597&rep=rep1&type=pdf

a) Ismételten oldja meg a 3.16. feladatot a hegymászó keresés segítségével. Le fog-e ragadni az ágens valamikor egy lokális maximumban? Lehetséges, hogy leragadjon az ágens konvex akadályok esetén?

Az akadályok konvexitása miatt a hegymászó keresés nem tud beragadni. Ehhez ugyanis az kellene, hogy egy adott pontból elérhető összes többi pont 'hátrébb' legyen a célállapothoz képest, mint az aktuális, ez pedig azt jelentené, hogy az akadály, amelynek egyik csúcsában az ágens áll, konkáv! Így viszont lényegében megegyezik a mélységi bejárással.

b) Hozzon létre olyan konkáv környezetet, amelyben az ágens leragad!

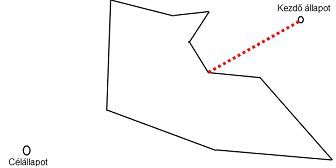
Folytonos fekete vonal jelzi az akadályt, piros vonal jelzi az algoritmus első lépését, ami után elakad! (Mindkét szomszédos állapot távolabb van a céltól, mint az aktuális, így a hegymászó algoritmus lokális maximumba került.)

c) Módosítsa úgy a hegymászó algoritmust, hogy az 1 mélységű keresés helyett k mélységű keresést használjon annak eldöntésére, hogy a következő lépésben hová menjen. Meg kell keresnie a legjobb k lépéses utat, e mentén egy lépést megtenni, majd az eljárást megismételni.

A módosítás tehát azt jelenti, hogy megkeressük az összes csúcsot, amely az aktuálistól legfeljebb k távolságra van, és ebből a halmazból választjuk ki a legjobbat, majd az ehhez vezető első csúcsot választjuk ki következő lépéshez.

d) Létezik k-nak olyan értéke, ami mellett az új algoritmus garantáltan elkerüli a lokális maximumokat?

Legyen K az összes konkáv akadályok csúcsai számának maximuma. Ekkor k = K/2 + 1 lépés mindig elegendő lesz a lokális maximumok elkerüléséhez, ugyanis az előretekintő keresés k lépésben valamelyik irányból biztosan megkerüli az akadályt.

e) Magyarázza meg, hogy ebben az esetben a TRTA* algoritmus hogyan teszi lehetővé az ágens számára, hogy a lokális minimumokból kimeneküljön.

A lokális minimumokból kilépni nyílván igen egyszerű: vegyük a legkevésbé rossz lehetséges lépést. A probléma abból adódik, hogy ha ezt a lépést nem jegyezzük meg, legközelebb ugyanúgy visszalépünk a lokális minimumba. Ezt igyekszik elkerülni a TRTA* algoritmus. Amikor az ágens először érkezik meg egy adott pontba, még a h() heurisztikát használja, de ezután bevezet egy tapasztalati heurisztikát, H()-t, amit később módosítani tud. Ha épp elhagy egy lokális minimumot, növeli annak H() értékét (kilapítja a síkot). Így ha elégszer próbálkozik ugyanazzal a lokális minimummal (zsákutcával), a H() érték elég nagyra nő, hogy ne próbálkozzon arra többet (megtanulja elkerülni a zsákutcát).

Készítette: Ács Gergely András, BME